UNIT 7
DFS
A real, N-periodic, discrete-time signal x[n] can be represented by a linear combination of the complex exponential signals
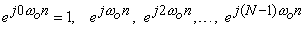
As
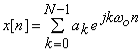
In these expressions, 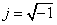 , and the discrete-time fundamental frequency is
, and the discrete-time fundamental frequency is 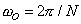 . This discrete-time Fourier series representation provides notions of frequency content of discrete-time signals, and it is very convenient for calculations involving linear, time-invariant systems because complex exponentials are eigenfunctions of LTI systems.
. This discrete-time Fourier series representation provides notions of frequency content of discrete-time signals, and it is very convenient for calculations involving linear, time-invariant systems because complex exponentials are eigenfunctions of LTI systems.
The complex coefficients 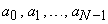 can be calculated from the expression
can be calculated from the expression
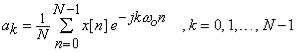
The 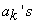 are called the spectral coefficients of the signal x[n]. A plot of
are called the spectral coefficients of the signal x[n]. A plot of 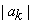 k is called the magnitude spectrum of x[n], and a plot of
k is called the magnitude spectrum of x[n], and a plot of 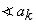 k is called the phase spectrum of x[n]. These plots, particularly the magnitude spectrum, provide a picture of the frequency composition of the signal. Notice that the spectral coefficients repeat as k is varied. In particular, for any value of k,
k is called the phase spectrum of x[n]. These plots, particularly the magnitude spectrum, provide a picture of the frequency composition of the signal. Notice that the spectral coefficients repeat as k is varied. In particular, for any value of k,
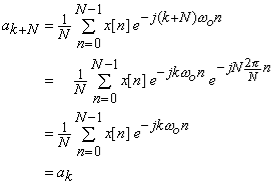
The discrete Fourier transform transforms a sequence of N complex numbers 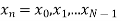 into another sequence of complex numbers
into another sequence of complex numbers
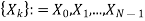 , which is defined by
, which is defined by
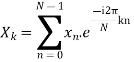
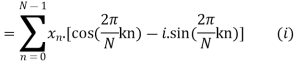
Example:
Let N =4 and
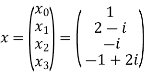
Here we demonstrate how to calculate the DFT of x using equation (1)
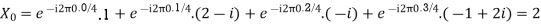
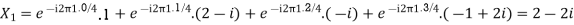
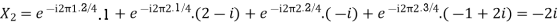
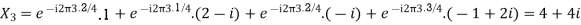
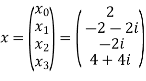
Properties of DFT
Linear Property
If x (t) -> X (w)
Y (t) -> Y (w) then
a x (t) + b y (t) -> a X (w) +b Y (w)
Time Shifting Property
If x (t) ⟷F.TX (ω)
Then Time shifting property states that
x (t−t0)⟷F.T e−jω0t X(ω)
Frequency Shifting Property
If x (t) ⟷X (ω)
Then frequency shifting property states that
Ejω0t.x (t) ⟷X (ω−ω0)
Time Reversal Property
If x (t) ⟷X (ω)
Then Time reversal property states that
x (−t)⟷X(−ω)
Differentiation Property
If x (t) ⟷X (ω)
Then Differentiation property states that
Dx (t) dt ⟷jω.X(ω)
dnx (t)dtn⟷(jω)n.X(ω)
Integration Property
Integration property states that
∫x (t) dt⟷1jω X (ω)
Then
∭...∫x (t) dt ⟷ (jω) n X (ω)
Multiplication and Convolution Properties
If x (t) ⟷X (ω)
y (t)⟷Y (ω)
Then multiplication property states that
x (t).y (t)⟷X (ω) ∗Y (ω)
And convolution property states that
x (t)∗y(t)⟷1/2πX(ω).Y(ω)
Numericals:
- Compute the N-point DFT of x (n) =3 δ (n).
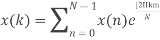
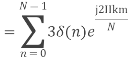
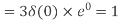
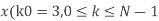
2. Compute the N-point DFT of x(n)=7(n−n0)
Solution −We know that,
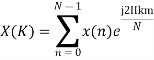
Substituting the value of x(n),
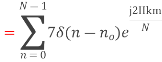
Properties of FFT
Certain algorithms permit implementations of Discrete Fourier transform with considerable savings in computation time. These algorithms are known as Fast Fourier Transform.
FFT algorithm are based on fundamental principle of decomposing the computation of DFT of sequence length into successively smaller discrete Fourier transforms.
They are basically two classes of FFT algorithms
- Decimation in time
- Decimation in frequency
Decimation-in-time algorithm
This algorithm is known as Radix-2 DIT-FFT algorithm which means the number of output points N can be expressed as a power of 2 that is N = 2M where M is an integer.
Let x(n) be a sequence where N is assumed to be a power of 2. Decimate or break this sequence into two sequences of length N/2 where one sequence consists of even-indexed values of x(n) and the other of odd-indexed values of x(n).
Xe(n) = x(2n) n= 0,1,……….. N/2-1
Xo(n) = x(2n+1) n= 0,1,……….. N/2 -1
The N-pt DFT of x(n) can be written as
X(k) = 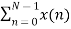 WN nk where k=0,1……….. N-1.
WN nk where k=0,1……….. N-1.
Separating x(n) into even and odd indexed values of x(n) we obtain
X(k) = 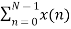 WN nk +
WN nk + 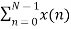 WN nk
WN nk
( n even) (n odd)
= 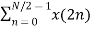 WN 2nk +
WN 2nk + 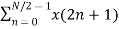 WN (2n+1)k
WN (2n+1)k
= 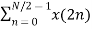 WN 2nk + Wnk
WN 2nk + Wnk 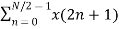 W N 2nk
W N 2nk
X(k) = 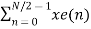 WN 2nk + Wnk
WN 2nk + Wnk 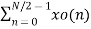 W N 2nk
W N 2nk
WN2 =( e-j2π/N) 2 = e-j2π/N/2 = W N/2 .
WN2 = W N/2
X(k) = 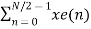 W N/2n k + WNk
W N/2n k + WNk 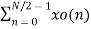 WN/2kn
WN/2kn
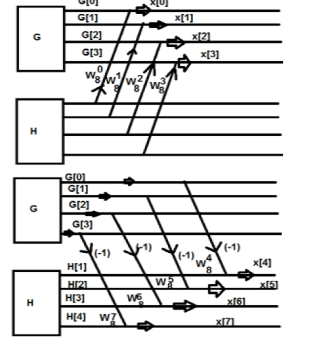
W84 = -1
W8 5 = - W 81
W86 = - W82
W87 = - W83
G(0) – H(0) = x(4)
G(1) - W 81 H(1) = x(5)
G(2) - W82 H(2) = x(6)
G(3) - W83 H(3) = x(7)
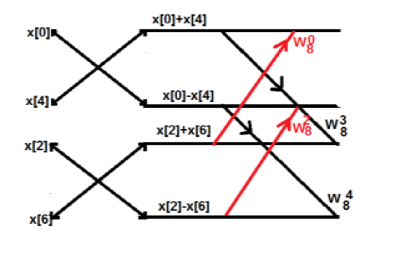
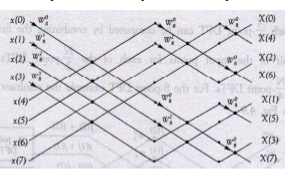
Consider the sequence x[n]={ 2,1,-1,-3,0,1,2,1}. Calculate the FFT.
Arrange the sequence as x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7)
Since N=8 find the values W8 0 to W 87
Apply the butterfly diagram to obtain the values.
Decimation in Frequency FFT
Apart from time sequence, an N-point sequence can also be represented in frequency. Let us take a four-point sequence to understand it better.
Let the sequence be x[0],x[1],x[2],x[3]………..x[7]
Mathematically, this sequence can be written as;
X(k) = 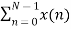 WN n-k where k=0,1……….. N-1.
WN n-k where k=0,1……….. N-1.
Now let us make one group of sequence number 0 to 3 and another group of sequence 4 to 7. Now, mathematically this can be shown as
= 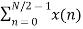 WN nk +
WN nk + 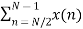 WN nk
WN nk
Let us replace n by r, where r = 0, 1 , 2….N/2−1.
= 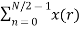 W N/2 nr
W N/2 nr
We take the first four points x[0],x[1],x[2],x[3] initially, and try to represent them mathematically as follows –
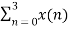 W 8 nk +
W 8 nk + 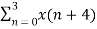 W8 (n+4) k
W8 (n+4) k
= 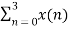 +
+ 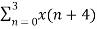 W8 (n+4) k
W8 (n+4) k
= 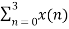 + {
+ { 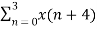 W8 (4) k } W8 nk
W8 (4) k } W8 nk
X[0] = 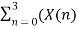 + X[n+4]
+ X[n+4]
X[1] = 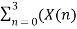 + X[n+4]) W8 nk
+ X[n+4]) W8 nk
= X(0) – X(4) + (x[1] – X[5]) W8 1 + ( X[2] – X[6] )W82 + X(3) – X(7) W8 3
DIF –FFT Algorithm
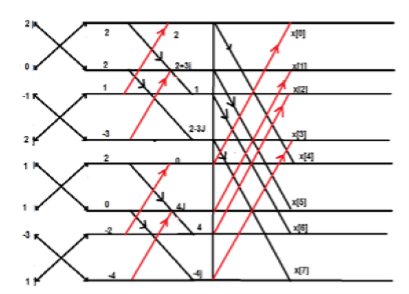
Find the DIF –FFT of the sequence x(n)= { 1,-1,-1,1,1,1,-1} using Dif-FFT algorithm.
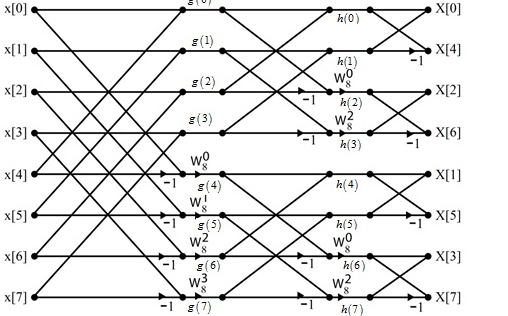
X(0)= 20 X(4) =0
X(1) = -5.828- j2.414 X(5) = -0.1716 + j 0.4141
X(2) = 0 X(6) = 0
X(3) = -0.171 – j 0.4142 X(7) = -5.8284 + j2.4142