Unit 2

DSV

2.1 Discrete Random variables:

A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,........ Discrete random variables are usually counts.

If a random variable can take only a finite number of distinct values, then it must be discrete.

Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor's surgery, the number of defective light bulbs in a box of ten.

2.2 Probability mass function

The probability distribution of a discrete random variable is a list of probabilities associated with each of its possible values. It is also sometimes called the probability function or the probability mass function.

Suppose a random variable X may take k different values, with the probability that X = xi defined to be P(X = xi) = pi. The probabilities pi must satisfy the following:

1: 0 < pi < 1 for each i

2: p1 + p2 + ... + pk = 1.

Example

Suppose a variable X can take values 1,2,3, or 4. The probabilities associated with each outcome are described by the following table:

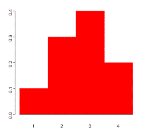
Outcome  1 2 3 4

Probability 0.1 0.3 0.4 0.2

The probability that X is equal to 2 or 3 is the sum of the two probabilities: 

P(X = 2 or X = 3) = P(X = 2) + P(X = 3) = 0.3 + 0.4 = 0.7.

Similarly, the probability that X is greater than 1 is equal to 1 - P(X = 1) 

= 1 - 0.1 = 0.9, 

2.3 Probability Distribution Function

Probability distributions indicate the likelihood of an event or outcome. Statisticians use the following notation to describe probabilities:

p(x) = the likelihood that random variable takes a specific value of x.

Probability distributions describe the dispersion of the values of a random variable. Consequently, the kind of variable determines the type of probability distribution.

For a single random variable, statisticians divide distributions into the following two types:

• Discrete probability distributions for discrete variables
• Probability density functions for continuous variables

Discrete probability functions are also known as probability mass functions and can assume a discrete number of values.

For example, coin tosses and counts of events are discrete functions. These are discrete distributions because there are no in-between values.

For example, you can have only heads or tails in a coin toss. Similarly, while counting the number of books that a library checks out per hour, you can count 21 or 22 books, but nothing in between.

For discrete probability distribution functions, each possible value has a non-zero likelihood. Furthermore, the probabilities for all possible values must sum to one. Because the total probability is 1, one of the values must occur for each opportunity.

For example, the likelihood of rolling a specific number on a die is 1/6. The total probability for all six values equals one. When you roll a die, you inevitably obtain one of the possible values.

Continuous probability functions are also known as probability density functions. In continuous distribution the variable assumes an infinite number of values between any two values. Continuous are often measurements on a scale, such as height, weight, and temperature.

Unlike discrete probability distributions where each particular value has a non-zero likelihood, specific values in continuous distributions have a zero probability.

For example, the likelihood of measuring a temperature that is exactly 32 degrees is zero.

2.4 Examples of random variables and distributions

Random variable

Suppose to each point of a sample space we assign a number. We then have a function defined on the sample space. This function is called a random variable (or stochastic variable) or more precisely a random function (stochastic function).

It is usually denoted by a capital letter such as X or Y. In general, a random variable has some specified physical, geometrical, or other significance.

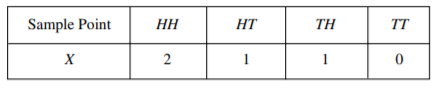
For example,suppose that a coin is tossed twice so that the sample space is S= {HH, HT, TH, TT}.

Let X represent the number of heads that can come up. With each sample point we can associate a number for X as shown in Table. Thus, for example, in the case of HH (i.e., 2 heads), X= 2 while for TH (1 head), X = 1. It follows that X is a random variable.

A random variable that takes on a finite or countably infinite number of values is called a discrete random variable while one which takes on a non-countably infinite number of values is called a non-discrete random variable.

Discrete Probability Distributions

Let X be a discrete random variable, and suppose that the possible values that it can assume are given by x1, x2, x3, . . . , arranged in some order.

Suppose also that these values are assumed with probabilities given by P(X =xk)  =f(xk) k = 1, 2, . . . (1)

It is convenient to introduce the probability function, also referred to as probability distribution, given by P(X = x) = f(x) ………(2)

For x =xk, this reduces to (1) while for other values of x, f(x)  0.

In general, f(x) is a probability function if

1. f(x) 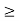0

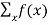2. =1

Where the sum in 2 is taken over all possible values of x.

Problem :

Find the probability function corresponding to the random variable X, Assuming, that the coin is fair

P(HH ) =1/4   P(HT) =1/4    P(TH) =1/4     P(TT) =1/4

Then

P(X=0) = P(TT) =1/4

P(X=1) = P(HT U TH) = P(HT) + P(TH) = ¼ + ¼ = ½

P(X=2) = P(HH) =1/4

We have then the probability function is thus given by

2.5 Continuous Random Variables

A continuous random variable is as function that maps the sample space of a random experiment to an interval in the real value space. A random variable is called continuous if there is an underlying function f(x) such that

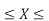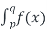P(p q) = dx

f(x) is non-negative function called the probability density function.  From the rules of probability

P(-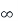< X < ∞) = 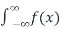dx =1

2.6 Probability density function

In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function that describes the relative likelihood for this random variable to take on a given value.

Probability density function is defined by following formula:

P(a≤X≤b)=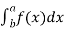

Where −

• [a,b][a,b] = Interval in which x lies.
• P(a≤X≤b)= probability that some value x lies within this interval.
• Dx = b-a

Example

During the day, a clock at random stops once at any time. If x be the time when it stops and the PDF for x is given by:

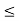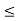f(x) = {1/24, 0, for 0 x 24

0                     otherwise

Calculate the probability that clock stops between 2 pm and 2:45 pm.

Solution:

We have found the value of the following:

P(14 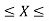14.45 )

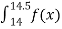=   dx

= 1/24 (0.45)

= 0.01875

2.7 Examples on Distributions

The weight of a pot of water chosen is a continuous random variable. The following table gives the weight in kg of 100 containers recently filled by the water purifier. It records the observed values of the continuous random variable and their corresponding frequencies. Find the probability or chances for each weight category.

We first divide the number of containers in each weight category by 100 to give the probabilities.

References