Unit - 2
Stability Constraints in Synchronous Grids
The differential equation that relates the angular momentum (M) the acceleration power (Pa) and the rotor angle (δ) is known as swing equation.
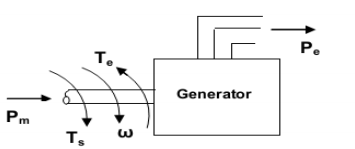
Consider the generator shown in the above figure. It receives mechanical power Pm at the shaft torque Tm and the angular speed ω via shaft from the prime-mover. It delivers electrical power Pe to the power system network. The generator develops electromechanical torque Te in opposition to the shaft torque Ts. At steady state, Tm = Te
Accelerating torque acting on the rotor is given by
Ta = Tm – Te
Multiplying by ω on both sides, we get power acceleration (Pa):
Pa = Pm – Pe
Pa=Ta ω = J*α*ω= M* α
Therefore,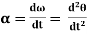 
= angular acceleration
, (
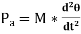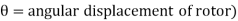
Θ – it is more convenient to measure the angular position of rotor with respect to synchronously rotation frame.
(δ=θ-ωt) of reference, ωt=0, hence
(δ=θ) then,
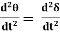
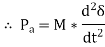
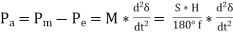, This equation is known as Swing Equation
Incase damping power D is to be added then the equation is
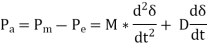
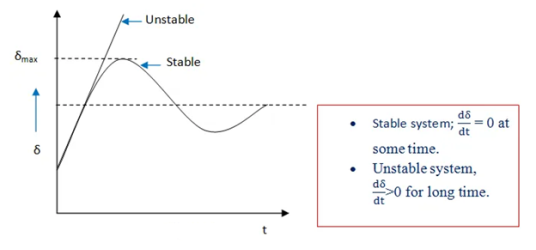
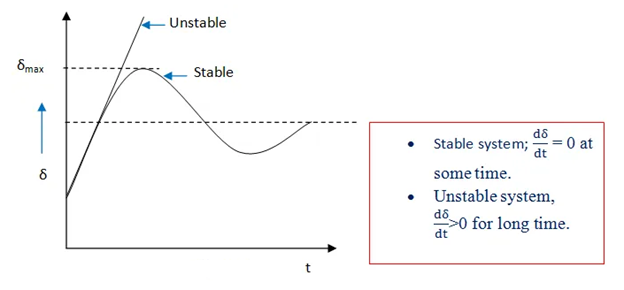
Swing curve, plot of power angle δ vs time t, can be obtained by solving the swing equation. Fig. (a) Stable system and (b) unstable system.
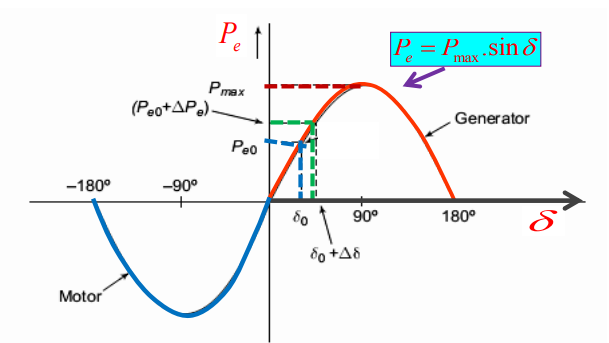
Swing curves are used to determine the stability of the system. If the rotor angle δ reaches a maximum and then decreases, then it shows that the system has transient stability (figure-a). On the other hand, if the rotor angle δ increases indefinitely, then it shows that the system is unstable (figure-b).
Studying the stability of a generator connected to an infinite bus
Complex power is given by
S=P+jQ=VI* or P-jQ =V*I
Thus, the real power, P= Re (V*I)
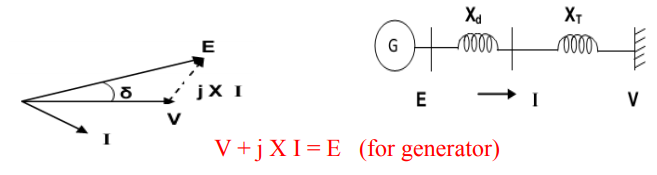
Where
V- is the voltage at infinite bus,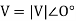 
E- is the external voltage of generator,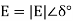 
X- is the total reactance
The internal voltage E leads V by angle δ, thus
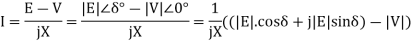
Electric Output Power,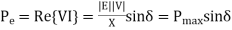 
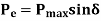
As a result of Swing Equation for generator is
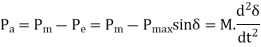
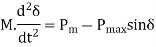
The graphical plot of power angle equation in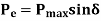 
for generator & motor is shown in figure
Key Takeaway
Swing curves are used to determine the stability of the system. The differential equation that relates the angular momentum (M) the acceleration power (Pa) and the rotor angle (δ) is known as swing equation.
a) Reducing the magnitude of disturbance: Large disturbances are typically due to faults which are cleared by line tripping. Reducing the duration of fault is one method of preventing loss of synchronism. These days, it is possible to clear faults within 3-5 cycles (taking into account relay and circuit breaker opening times).
b) Planning: This would mean augmenting the transmission network with new transmission lines. Increasing the power transfer capability of transmission lines by compensating transmission reactance with series capacitors and shunt capacitors.
c) Control: The short term or excess capacity of many equipment can be used to enhance stability by appropriate controls. For example, excitation systems can allow for short-term boosting of field voltage. Also, capacitors can be switched into the network in series and shunt. The switching may be done by means of circuit breakers or power electronic controls (power electronic controllers also allow for continuous control; this will be discussed in later modules).
d) Operation: During operation, it is ensured that the system is operated such that there exists sufficient "margin" for the system to withstand a credible disturbance (like a fault). This imposes a constraint on the level of power transfers which are permissible -- for larger levels of power flow, the synchronous generators are more likely to lose synchronism after a large disturbance. A system operator continuously monitors a power system and ensures that this is unlikely to happen. If the system is unlikely to withstand a credible disturbance, then preventive control actions like reducing the power transfer levels are taken. This may be achieved by re-scheduling power generated at various generators.
Key Takeaway
Planning, Control, Operation- Reduces the duration of fault to prevent loss of synchronism in a power system.
1. Euler’s Method:
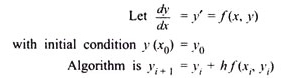
2. Modified Euler’s Method:
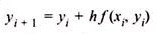
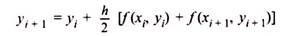
Key Takeaway
There are two methods where slope is approximated at the middle of interval & the algorithm helps in predicting the faults and analysis in power system
The swing equation can be written as-
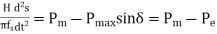, input power is assumed to be constant
The above equation can be split into 2 single order equations-
1) 
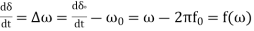
2) 
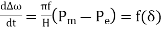
We have ω & δ as a function of time t. Let us assume that x=t, y=δ & z=ω.
Hence,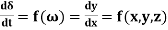 
and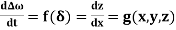 
The first step in the transient stability study is the load flow equation to obtain system condition disturbance. Each bus must be defined by P, Q, V, δ and 2 of them should be known. Let us assume that the ith machine is represented by a constant voltage source behind transient reactance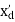 
.
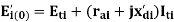, where
Eti= terminal voltage of i – th machine
rai= armature resistance of i-th machine
Iti= current through i-th machine
Also,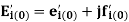 
in rectangular form
The initial internal voltage angle (power angle) is given by-
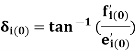
Machine current before disturbance calculated from-
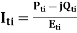for i=1, 2, 3…, m,
Where Pti & Qti are real & reactive power generation of i-th machine & Eti is the terminal voltage of i-th machine, taken as reference phasor
𝑃 (0) initial mechanical input power= electrical air gap power 𝑃𝑒𝑖 prior to disturbance and can be obtained from-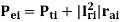 
For steady state, 𝛿0 = (0). For the transient analysis (when disturbance occurs due to fault), the network admittance matrix must be now changed to include equivalent circuit of machines and changes in loads. Each element representing a machine is a branch of a new bus and each element representing a load is a link to ground. According to Runge-kutta derivation, it is required to solve 2 simultaneous differential equations.
General expression of a Runge-Kutta 4th order numerical technique
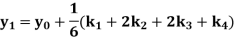
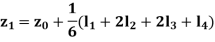
Where,
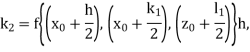
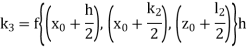
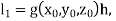
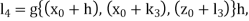
According to Runge-Kutta 4th order numerical technique
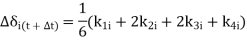
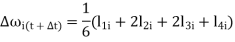
k’s & i’s are the changes δi & ωi respectively obtained using derivatives evaluated at predetermined points.
Key Takeaway
This method helps in transient analysis of a power circuit.
The Equal Area Criterion is concerned with transient stability. It is in fact a very easy graphical method used. It is for deciding the transient stability of single machine or else two-machine system against infinite bus. Over a lossless line, the real power transmitted will be Pe=Pm sinδ. Consider a fault occurs in a synchronous machine which was operating in steady state. Here, the power delivered is given by Pe=Pm. For clearing a fault, the circuit breaker in the faulted section should have to be opened up. This process takes 5/6 cycles and the successive post-fault transient will take an additional few cycles. The prime mover which is giving the input power is driven with the steam turbine. For turbine mass system, the time constant is in the order of few seconds and for the electrical system, it is in milliseconds. Thus, while the electric transients take place, the mechanical power remains stable. The transient study mainly looks into the capability of the power system to retrieve from the fault and to give the stable power with a new probable load angle (δ).
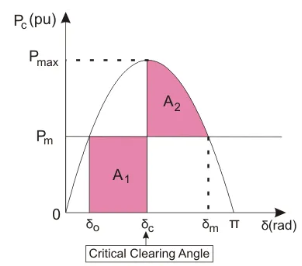
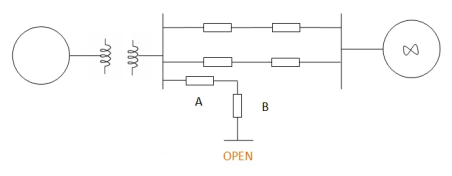
breakers opened and the real power is decreased to zero. But the Pm will be the power angle curve is considered which is shown in fig.1. Imagine a system delivering ‘Pm’ power on an angle of δ0 (fig.2) is working in a steady state. When a fault occurs; the circuit stable. As a result, accelerating power, Pa=Pm
The power differences will result in rate of change of kinetic energy stored within the rotor masses. Therefore, due to the stable influence of non-zero accelerating power, the rotor will accelerate. Consequently, the load angle (δ) will increase.
Now, we can consider an angle δc at which the circuit breaker re-closes. The power will then come back to the usual operating curve. At this moment, the electrical power will be higher than the mechanical power. But, the accelerating power (Pa) will be negative. Therefore, the machine will get decelerate. The load power angle will still continue to increase because of the inertia in the rotor masses. This increase in load power angle will stop in due course and rotor of the machine will start to decelerate or else the synchronization of the system will get lose.
The Swings equation is given by-
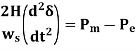
Multiply both sides by dt & integrate it for two arbitrary load angles which are δ0 & δc
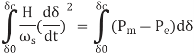
Assume at the time of fault the machine will accelerate & after clearing of fault it will decelerate. Hence the required equations are
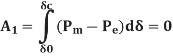
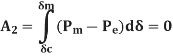
The system will reach steady state.
When A2 = A1, the margin of the stability limit is defined by this condition. Here, the clearing angle is given by δcr, the critical clearing angle.
Since, A2 = A1, we will get
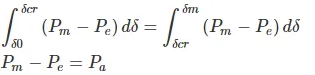
The critical clearing angle is related to the equality of areas, it is termed as equal area criterion. It can be used to find out the utmost limit on the load which the system can acquire without crossing the stability limit.
Key Takeaway
The Equal Area Criterion is concerned with transient stability. It is in fact a very easy graphical method used. It is for deciding the transient stability of single machine or else two-machine system against infinite bus.
During operation, it is ensured that the system is operated such that there exists sufficient margin for the system to withstand a disturbance. It is ensured that phase angular difference across transmission paths is not too large. Thus, angular stability puts a limit on the levels of power which can be transferred securely. One of the constraints for long distance AC transmission (other than thermal / voltage constraints) is the large phase angular difference which is required to transmit a given amount of power. The modified load ability of a line by taking into account stability limits is shown in the figure on the right. It is not easy to specify stability limits as they depend on the parameters of power system components and the operating conditions. However, for convenience it is specified by the maximum phase angular difference which is allowed across the line.
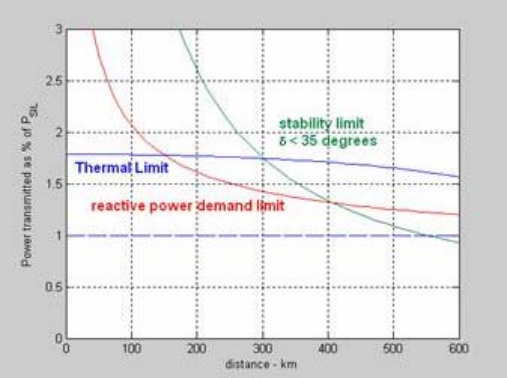
It is clear that stability is the major constraint for lines more than 300 km long.
Long distance transmission requires us to use high voltages and lower currents (otherwise resistive losses will be too large). So, step-up will still be required (it is not feasible (as yet) to generate power by ac or dc machines at high voltage). So, transformers will be used to step-up generated ac voltage to higher ac voltage, and then rectify it to DC using power electronic converters. DC is again inverted to ac at the receiving end of the line. Thus, a dc interconnection will require 2 large ac to dc converters at either end. Voltage profile along a line is not an issue since series inductive and shunt capacitive effects are not manifested in steady state for DC transmission. Resistive drop is usually small. Power Flow can be controlled using firing angle of thyristors used in the rectifier and inverter. Power flow is independent of the phase angular difference between sending (rectifier) and receiving (inverter) ends. So angular stability constraint is not there. In fact, if two areas are connected by only dc inter-connections, then even frequency of the two areas need not be the same.
Key Takeaway
During operation, it is ensured that the system is operated such that there exists sufficient margin for the system to withstand a disturbance. It is ensured that phase angular difference across transmission paths is not too large. Thus, angular stability puts a limit on the levels of power which can be transferred securely
(a) Series Compensation
Series compensated transmission lines utilize series capacitors to cancel a portion of the inductive reactance of the transmission line, so by means of compensation it can improve the power transmission capability of the line. Series compensation has been applied mostly to long transmission lines and other locations where the transmission distances, are great and where large power transfers over these distances are required. Modern HV and EHV transmission lines are series compensated to improve power system performance, to enhance power transfer capacity, to enhance power flow control and voltage control and to decrease capital investment.
The Power along the transmission line with series compensation is often explained by in terms of the system shown below figure. The active power P transferred by the compensated transmission lines are computed as
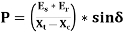
Effect of Series Compensation
1. The lower line impedance improves stability. When capacitor bank is inserted into the transmission line, the rotor angle (δ) reduces for the same amount of power transfer due the effect of compensation. Reduction in angle δ allows rotor to operate at a lower rotor angle with increased stability limit.
2. The lower line impedance improves voltage regulation. By inserting capacitor bank into the transmission line net impedance of the line reduces resulting into lesser voltage drop along the transmission line and better voltage regulation.
3. Adding series capacitance provides a method of controlling the division of load among several lines. By controlling degree of compensation of capacitor bank installed in a several bus systems, amount of the load shared among the lines can be controlled. It gives the better control of load among several lines.
4. Increasing the loading capacity of a line improves the utilization of the transmission system and therefore the return on the capital investment. Series compensated transmission lines allow power transfer at the same voltage level over longer transmission lines than uncompensated lines. This better utilizes the existing transmission network, which is cost effective and quicker rather than building new or additional parallel lines
5. Increase power transfer capacity.
(b) Generation Rescheduling
Generators are rescheduled such that it doesn’t exceed the transfer limits of the transmission line. It is done based on creating a population containing generation limits which satisfies the demand. The rescheduling of generators makes the generation to operate at an equilibrium away from the one determined by equal incremental costs. Mathematical models are involved for obtaining the corresponding cost signals. The results are used in congestion pricing as an indicator for the market participants in rearranging the power injections & extractions. Rescheduling cost is the cost involved in rescheduling the generation.
Key Takeaway
Series compensated transmission lines utilize series capacitors to cancel a portion of the inductive reactance of the transmission line, so by means of compensation it can improve the power transmission capability of the line
References:
1. Power system Analysis-by John J Grainger William D Stevenson, TMC Companies, 4th edition.
2. The Power System Analysis and Design by B.R. Gupta, Wheeler Publishing
3. Power System Analysis by Hadi Saadat – TMH Edition.
4. Modern Power System Analysis by I.J. Nagaraj and D.P.
