UNIT 1
Introduction, CRYPTO BASICS
Beforediscussingconceptofencryptionmethodswemustknowwhicharethedifferenttypesofcryptography?Therearetwotypesofcryptographyi.e.symmetrickeycryptographyandasymmetrickeycryptographyasshowninFig.
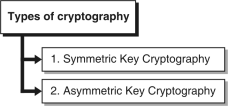
Fig.:Typesofcryptography
SymmetricKeyCryptography
Symmetrickeycryptographyalsocalledassecretkeycryptography.
Insymmetrickeycryptographyasinglekeyisusedforencryptionaswellasdecryption.
AsshowninFig.2.2.2senderencryptplaintextusingsharedsecretkeyandtheresultantciphertextistransmittedthroughcommunicationmediumsuchasInternet,atthereceiversidetheciphertextisdecryptedusingsamedecryptionkeytoobtainoriginalplaintext.
NotethatencryptionanddecryptionprocessuseswellknownsymmetrickeyalgorithmcalledasDataEncryptionStandard(DES).
Mathematically itisrepresentedasP=D(K,E(P)).
Where P = Plain Text, E (P) = Encryption of plain text, D (K, E(P)) = Decryption of Plain text using shared
key K.
ForExample:
Streamandblockcipher,DataEncryptionStandard(DES),AdvanceEncryptionStandard(AES)andBLOFISH.
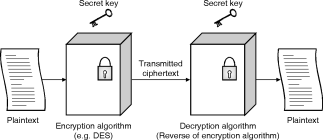
Fig:SymmetricCipherModel
Herethepossibilityisthatifanattacker/opponentgotciphertext??He/shemayapplydifferentpermutationsandcombinationstodecryptandobtaintheoriginalplaintext.Herethemainaimofcryptographyiscameintopicture.Alwayssenderhastothinkonapplyingdifferentencodingtechniqueonplaintextmessageandconvertitintociphertextmessagesothatattackercannotreadtheactualplaintexteasily.
Symmetricciphermodelconverttheplaintextmessageintociphertextbyusingfollowingtechniques.
AdvantagesofSymmetrickeycryptography
Symmetrickeyisfasterthanasymmetrickeycryptography.
Becauseofsinglekeydatacannotdecrypteasilyatreceiversideevenifitisinterceptedbyattacker.
Asthesamekeyisusedforencryptionanddecryptionreceivermusthavethesenderskeyhecannotdecryptitwithoutsenderpermission.
Symmetrickeyachievetheauthenticationprinciplebecauseitchecksreceiversidentity
DESandAEStechniquesareimplementedusingsymmetrickeycryptography.
Systemresourcesarelessutilizedinsymmetrickeycryptography.
DisadvantagesofSymmetrickeycryptography
Oncethekeyisstolenwhiletransmittingdatabetweensenderandreceiveritisveryeasytodecryptthemessageassamekeyisusedforencryptionanddecryption.
Insymmetrickeycryptography,keyistransmittedfirstandthenmessageistransfertothereceiver.Ifattackerinterceptsthecommunicationbetweensenderandreceiverthenhecandecryptthemessagebeforeitreachestointendedrecipients
AsymmetricKeyCryptography
Asymmetrickeycryptographyisalsocalledaspublickeycryptography.
Inasymmetrickeycryptographytwokeysareused,oneforencryptionandotherfordecryption.
Asmentionedasymmetrickeycryptographyinvolvesuseoftwokeysoneispublickeythatmayknowtoeveryoneandcanbeusedtoencryptmessages,andverifysignatures.Otherisprivatekeyknownonlytothereceiverofthemessageorverifier,usedtodecryptmessages,andsign(create)signatures.
Itisalsocalledasasymmetrickeycryptographybecauseonekeyisusedforencryptiononlyitscorrespondingkeymustbeusedfordecryption.Nootherkeycandecryptthemessage.
Thesenderandreceivercanencryptmessagesusingencryptionkey(public)orverifysignatures,hecannotdecryptmessagesorcreatesignaturesbecauseherequireddecryptionkey(private)whichisknownonlytothereceiverofthemessage.Publickeycryptosystem/asymmetrickeycryptographyisshowninFig.2.2.3.
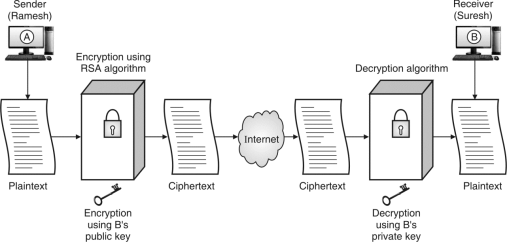
MathematicallyitisrepresentedasP=D(Kd,E(Ke,P))
WhereP=PlainText,E(P)=Encryptionofplaintext,D=Decryption,Ke=EncryptionkeyKd=DecryptionKey.
Forexample,senderRameshwantstocommunicatewiththereceiverSureshthentheymusthaveeachoneofthisi.e.privatekeyandpublickeythenandthencommunicationwillbesuccessful.Table2.2.1showsthepossiblepairofkeysthatRameshandSureshmustknowwhilecommunicatingwitheachother.
Table:Pairofprivateandpublickeys
KeyDetails | Ramesh(A)Shouldknow | Suresh(B)shouldknow |
RameshPrivateKey(A) | YesAmustknow | NotknowntoB |
RameshPublicKey(A) | YesAmustknow | YesitisknowntoSureshalso |
Sureshprivatekey(B) | NotknowntoRamesh(A) | YesSuresh(B)mustknow |
Sureshpublickey(B) | YesknowntoRamesh(A) | YesSuresh(B)alsoknownit |
Followingarethepossiblecasesofpublickeycryptographyasperthetablementionedabove.
Case1
1. WhenRameshwantstosendamessagetoSuresh.RameshcanencryptthemessageusingSureshpublickey.ThisispossiblebecauseRameshandSureshknowsthepublickey.
2. RameshcansendthismessagetoSuresh(KeepinmindthisitisencryptedusingSureshpublickey).
3 SureshcandecrypttheRameshmessagebyusingSureshownprivatekey.BecauseonlySureshknowshisprivatekeyRameshisnotawareaboutSureshprivatekey.
4. ItisimportanttonotethatthemessageonlydecryptedusingSureshprivatekeyandnothingelse.
Case2
IfSureshwantstosendthemessagetoRamesh,thenreversetheabovecase1.SureshcanencryptthemessageonlywithRameshpublickey.ThereasononlyRameshcandecryptthemessagetoobtainitsoriginalplaintextformatusinghisprivatekey.
Publickeycryptographyachievesauthentication(authenticationhelpstoidentifytheclaimedidentityofanentity,suchasusernamepasswordoranyotherimportantinformationsuchasencryptionordecryptionkeysstolenduringtransmissionbetweensenderandreceiver)andnon-repudiation(itpreventseithersenderorreceiverfromdenyingatransmittedmessage).
PrinciplesofpublickeycryptographyalsoincludemathematicalbackgroundtounderstandtheuseofkeypairsinalgorithmslikeRivestShamirAdlman(RSA)andDiffieHellmanAlgorithm.
ForExample:
RivestShamirAdlman(RSA)andDiffieHellmankeyexchangealgorithm.
AdvantagesofAsymmetrickeycryptography
InAsymmetrickeycryptography,keycannotbedistributeamongsenderandreceiverasbothhavetheirownkey,sothereisnoproblemofkeydistributionwhiletransmittingthedataoverinsecurechannel.
Themainadvantageofasymmetrickeycryptographyisthattwoseparatekeysareusedforusedencryptionanddecryption;evenifencryptionkeyisstolenbyattackerhe/shecannotdecryptthemessageasdecryptionkeyisonlyavailablewithreceiveronly.
RSAalgorithmandDiffieHellmankeyexchangeareimplementedusingasymmetrickeycryptography.
Easytouseforuserandscalabledoesnotrequiremuchadministrativework.
DisadvantagesofAsymmetrickey cryptography
Becauseofdifferentkeyusedbetweensenderandreceiverrequiremoretimetogetthetransmissiondoneascomparetosymmetrickeycryptography.(Slowerthatsymmetrickeycryptographyveryfewasymmetricencryptionmethodsachievethefasttransmissionofdata).
Asymmetrickeycryptographyutilizesmoreresourceascomparetosymmetrickeycryptography.
DifferencebetweenSymmetricandAsymmetricKeyCryptography
Sr.No. | SymmetricKeyCryptography | AsymmetricKeyCryptography |
1. | InSymmetrickeycryptographysingleorsamekeyisusedforencryptionanddecryption | Inasymmetrickeycryptographytwokeysareused,oneisforencryptionandotherisfordecryption |
2. | Symmetrickeycryptographyisalsocalledassecretkeycryptographyorprivatekeycryptography. | Asymmetrickeycryptographyisalsocalledaspublickeycryptographyorconventionalcryptographicsystem. |
3. | Mathematicallyitisrepresentedas P=D(K,E(P)). WhereKisencryptionanddecryptionkey. P=plaintext, D=Decryption E(P)=Encryptionofplaintext | Mathematicallyitrepresentedas P=D(Kd,E(Ke,P)), WhereKeandKdareencrytptionanddecryptionkey. D=Decryption E(Ke,P)=EncryptionofplaintextusingprivatekeyKe. |
4. | Symmetrickeyisfasterthanasymmetrickeycryptography.
| Becauseoftwodifferentkeyusedasymmetrickeyisslowerthanasymmetrickeycryptography. |
5. | Forencryptionoflargemessageasymmetrickeycryptographystillplayanimportantrole. | Inasymmetrickeycryptographyplaintextandciphertexttreatedasintegernumbers. |
6. | Symmetrickeycryptographyutilizeslessresourceascomparetoasymmetrickeycryptography. | Asymmetrickeycryptographyutilizesmoreresourceascomparetosymmetrickeycryptography. |
7. | ForExample:AES,DESand BLOWFISH | ForExample:RSA,DiffieHellmanKeyexchangealgorithm. |
Followingisthelistofpossiblecombinationshowingtheletters3placesdownofeachalphabet:
Plaintext | a | b | c | d | e | f | g | h | i | j | k | L | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
Ciphertext | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Thecorrespondingnumberequivalenttoeachalphabetisgivenbelow:
a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | X | y | z |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
C = E(3,P)=(P+3)mod26
P = D(3,C)=(C–3)mod26
Where C = Ciphertext/oralphabet
P = Plaintext/alphabet
E = Encryption
D = Decryption
Mod26becauseinEnglishtherearetotal26alphabets.
ItisveryeasytobreakciphertextobtainedfromplaintextmessagewiththehelpofBrute-Forceattackbecausetheattackerwillbehavingonly25possiblekeystodecrypttheciphertext.
Furthersomemorecharacteristicswhichleadtoeasybruteforceattacksare:
1. Theencryptionanddecryptionalgorithmsareknown.
2. Only25possiblekeys.
3. Andplaintextlanguageiseasytorecognizewithfewrepetitionofalphabethavingsameciphertextletter.
Brute-Force-attack
Abrute–force–attackmeanstryingeverypossiblekeyonapieceofciphertextuntilanintelligibletranslationintoplaintextisobtained.Soitsbetterifwecreatemorecomplexciphertextfromgivenplaintextwiththehelpofanothersubstitutiontechniquecalledmonoalphabeticcipher.
Asubstitutionisatechniqueinwhicheachletterorbitoftheplaintextissubstitutedorreplacedbysomeotherletter,numberorsymboltoproduceciphertext.Substitutionmeansreplacinganalphabetofplaintextwithanalphabetofciphertext.Substitutiontechniquealsocalledconfusion.ThebestexampleofsubstitutioncipherisCaesarcipherinventedbyJuliusCaesar.
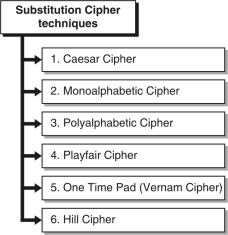
SubstitutionCiphertechniquesareasfollows :
 2
2
Fig.:SubstitutionCiphertechniques
CaesarCipher
JuliusCaesarintroducedtheeasiestandthesimplestuseofsubstitutioncipher.
InCaesarciphertechniqueeachletterisreplacedbytheletter/alphabetwhichisthreeplacesnexttothatletterwhichistobesubstituted.OrInCaesarciphertechnique,eachalphabetofaplaintextisreplacedwithanotheralphabetbutthreeplacesdownthelineasmentionedintablebelow.
Forexample
Plaintext:SunrisesintheEast
Ciphertext:VXQULVHVLQWKHHDVW
Followingisthelistofpossiblecombinationshowingtheletters3placesdownofeachalphabet:
Plaintext | a | b | c | d | e | f | g | h | i | j | k | L | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
Ciphertext | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
Thecorrespondingnumberequivalenttoeachalphabetisgivenbelow:
a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | X | y | z |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
MathematicallytheCaesarcipheralgorithmcanbeexpressedas
C = E(3,P)=(P+3)mod26
P = D(3,C)=(C–3)mod26
Where C = Ciphertext/oralphabet
P = Plaintext/alphabet
E = Encryption
D = Decryption
Mod26becauseinEnglishtherearetotal26alphabets.
ItisveryeasytobreakciphertextobtainedfromplaintextmessagewiththehelpofBrute-Forceattackbecausetheattackerwillbehavingonly25possiblekeystodecrypttheciphertext.
Furthersomemorecharacteristicswhichleadtoeasybruteforceattacksare:
1. Theencryptionanddecryptionalgorithmsareknown.
2. Only25possiblekeys.
3. Andplaintextlanguageiseasytorecognizewithfewrepetitionofalphabethavingsameciphertextletter.
Brute-Force-attack
Abrute–force–attackmeanstryingeverypossiblekeyonapieceofciphertextuntilanintelligibletranslationintoplaintextisobtained.Soitsbetterifwecreatemorecomplexciphertextfromgivenplaintextwiththehelpofanothersubstitutiontechniquecalledmonoalphabeticcipher.
MonoalphabeticCipher
InCaesarciphertheattackercaneasilyguesstheplaintextasitiseasilyrecognizable.InMonoalphabeticciphersubstitutesoneletterofthealphabetwithanyrandomletterfromthealphabet.
ItisnotnecessarythatifAissubstitutedwithBthencompulsorilyBhastobesubstitutedwithC.Itcanbereplacedwithanyotherletterofthealphabet.Theonlyweaknessinthisalgorithmisthatifmorerepetitionoccursthenattackercaneasilyguesstheplaintext.
Thisrandomsubstitutionisjustdonetohaveuniqueness.
Inthisthesubstitutionofcharactersarerandompermutationofthe26lettersofthealphabet.
For example
Followingisthesubstitutionthatwearetaking:
Plaintext | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
Cipher-text | e | o | u | n | a | f | p | v | b | m | w | l | c | q | x | d | g | k | s | y | z | i | t | r | j | h |
Plaintext:EastorWest
Ciphertext:aesyxktaay
CiphertextobtainwiththistechniqueyieldscompletelydifferenttextascomparetoCaesarcipher.Inthismethod,eachletterprovidesmultiplesubstitutesforasingleletter.
Forexample,
Acanbereplacedby:d,j,r,y
Bcanbereplacedby:h,u,m,petc.
Suchtypeoflargekeyspacemakesthisciphertechniqueextremelydifficulttobreakbybrute-forceattack.Butthiscanmakethecryptanalysisattackerstraightforwardtoguessthepattern.
PolyalphabeticCipher
Asinmonoalphabeticcipherweuseonlyonefixedalphabet,butdrawbackinmonoalphabeticisthesearefairlyeasytobreak.Sotomakeithardertobreaktheconceptofpolyalphabeticcipherarisesitisawaytousemorethanonealphabetandswitchingbetweenthemsystematically.
(A) Procedure of Polyalphabetic Cipher
1. Pickakeyword(forourexample,thekeywordwillbe“MEC”asshowninExample1).
2. Writeyourkeywordacrossthetopofthetextyouwanttoencipher,repeatingitasmanytimesasnecessary.
3. Foreachletter,lookattheletterofthekeywordaboveit(ifitwas'M',thenyouwouldgototherowthatstartswithan'M'),andfindthatrowintheVigeneretable.


4. Thenfindthecolumnofyourplaintextletter(forexample,'w',sothetwenty-thirdcolumn).
5. Finally,tracedownthatcolumnuntilyoureachtherowyoufoundbeforeandwritedowntheletterinthecellwheretheyintersect(inthiscase,youfindan'I'there).
Example1
Keyword | MECMECMECMECMECMECMECM |
Plaintext: | Weneedmoresuppliesfast |
Ciphertext | IIPQIFYSTQWWBTNUIUREUF |
Thus,theurgentmessage“Weneedmoresuppliesfast!”comesout:
IIPQIFYSTQWWBTNUIUREUF
(B) DifferencebetweenPolyalphabeticandMonoalphabetic
Sr.No. | PolyalphabeticCipher | MonoalphabeticCipher |
1. | Polyalphabeticcipherismoresecureandhardtobebroken. | Monoalphabeticcipherarenotverysecureandcanbeeasilybroken. |
2. | Morethanonealphabetisusedforsubstitution. | Onefixedsinglealphabetisusedforsubstitution. |
3. | Inapolyalphabeticcipher,thesubstitution | Inmonoalphabetic,thesamesubstitutionruleisusedforeachsubstitution. |
4. | Inpolyalphabeticorparticularalphabet,differentsubstitutioncanbedoneusingVigneretable. | Inmonoalphabetic,foraparticularalphabet,onlyonesubstitutioncanbeused. |
PlayfairCipher
ItwasinventedbyCharlesWheatstonein1854butknownbynamePlayfairbecauseLordPlayfairmadethistechniquepopular.ItwasusedbyBritisherinWorldWar1.
Itismultipleletterencryptiontechnique,whichuses5x5Matrixtabletostorethelettersofthephrasegivenforencryptionwhichlatteronbecomeskeyforencryptionanddecryption.
Forexample :
KeywordisFAIREXAMPLE.
Inthefirststepalllettersaretobefilledinthatmatrixfromlefttoright,theletterswhicharealreadybeenplacedisnotbeplacedagaininthatmatrix.
Afterfillingupofthegivenletter,fillrestofthespaceinthematrixwiththeremaininglettersalphabeticallywithnorepetitions.
ThelettersIandJwillbeconsideredasoneletter.SoIfIisalreadyplacedthennoneedtoplaceJinrestofthematrix.
Theletterswhicharealreadywritten/mentionedneednottobeplacingthatletteringivenmatrix.
ForingivenexampleAandEarealreadymentionedinmatrixsoitisnotmandatorytowritethatletteragaininthegivenmatrix.
Table
F | A | I | R | E |
X | M | P | L | B |
C | D | G | H | K |
N | O | Q | S | T |
U | V | W | Y | Z |
EncryptionusingTable keywordmatrix
1. Theplaintextreceivedistobebrokeninpairoftwoletters.
2. ForexampleCYBERcanbebrokenintoCYBER(X).
3. IfbothlettersaresameoronlyoneletterisleftthenputXwiththatalphabet.
4. Ifbothpairalphabetappearsinsamerowreplacetheletterwiththeimmediaterightalphabet(wrappingaroundtotheleftsideoftherowifaletterintheoriginalpairwasontherightsideoftherow).
5. Ifbothlettersappearinsamecolumnreplaceitwithalphabetimmediatebelowtothatletter(wrappingaroundtothetopsideofthecolumnifaletterintheoriginalpairwasonthebottomsideofthecolumn).
6. Ifnoneoftheconditionexplainedabovemeet,thenreplacethemwiththelettersonthesamerowrespectivelybutattheotherpairofcornersoftherectangledefinedbytheoriginalpair.
ForExample:
TheplaintextCYBERcanbeencryptedas:CYBER(X)
1. ForpairCYwecheckthatCYdoesnotoccurinsameroworcolumnsoweseestep6.
ThepairCYformsarectangle,replaceitwithHU.Ifpairformsarectangle,picksamerowletterbutoppositecorners.
F | A | I | R | E |
X | M | P | L | B |
C | D | G | H | K |
N | O | Q | S | T |
U | V | W | Y | Z |
SoCYwillencryptasHU.
2. CheckingforBEbothareinsamecolumnsoreplaceitwithimmediatenextinthatcolumn.
F | A | I | R | E |
X | M | P | L | B |
C | D | G | H | K |
N | O | Q | S | T |
U | V | W | Y | Z |
BEwillbeencryptedasKB(BelowtoEisB).
3. CheckingforR(X)
F | A | I | R | E |
X | M | P | L | B |
C | D | G | H | K |
N | O | Q | S | T |
U | V | W | Y | Z |
ThepairRXformsarectangle,replaceitwithFL.Ifpairformsarectangle,picksamerowletterbutoppositecorners.
R(X)willbeencryptedasFL.
SolvedExamplesonPlayfaircipher
Ex.
Encrypt"Thekeyishiddenunderthedoor"usingPlayfaircipherwithkeyword“domestic”.
Soln.:Keyword-domestic
Keywordisdomestic.
Inthefirststepalllettersaretobefilledinthatmatrixfromlefttoright,theletterswhicharealreadybeenplacedisnotbeplacedagaininthatmatrix.
Afterfillingupofthegivenletter,fillrestofthespaceinthematrixwiththeremaininglettersalphabeticallywithnorepetitions.
ThelettersIandJwillbeconsideredasoneletter.SoIfIisalreadyplacedthennoneedtoplaceJinrestofthematrix.
d | o | m | e | s |
t | i | c | a | b |
f | g | h | k | l |
n | p | q | r | u |
v | w | x | y | z |
ByusingPlayfairCipher(Usefollowingstepstoencryptgivenwordormessage)wewanttoencrypttheplaintextmessage“Thekeyishiddenunderthedoor”usingkeyworddomestic.
1. Theplaintextreceivedistobebrokeninpairoftwoletters,ifduplicateletterputx
2. Th,ek,ey,is,hi,dx,de,nu,nd,er,th,ed,ox,or
3. IfbothlettersaresameoronlyoneletterisleftthenputXwiththatalphabet.
4. Ifbothpairalphabetappearsinsamerowreplacetheletterwiththeimmediaterightalphabet(wrappingaroundtotheleftsideoftherowifaletterintheoriginalpairwasontherightsideoftherow).
5. Ifbothlettersappearinsamecolumnreplaceitwithalphabetimmediatebelowtothatletter(wrappingaroundtothetopsideofthecolumnifaletterintheoriginalpairwasonthebottomsideofthecolumn).
6. Ifnoneoftheconditionexplainedabovemeet,thenreplacethemwiththelettersonthesamerowrespectivelybutattheotherpairofcornersoftherectangledefinedbytheoriginalpair.
7. Referabovematrixforthesame.
ThStep6cf
EkStep5ar
EyStep5ae
IsStep6bo
HiStep6gc
DxStep6mv
DeStep4os
NuStep4pn
NdStep5vt
ErStep5ay
ThStep6cf
EdStep4so
OxStep6mw
OrStep6ep
Theplaintextmessage“Thekeyishiddenunderthedoor”encryptedas:
Cf,ar,ae,bo,gc,mv,os,pn,vt,ay,cf,so,mw,ep.
Ex.
Isplayfairciphermonoalphabeticcipher?Justify.Constructaplayfairmatrixwiththekey“moonmission”andencryptthemessage“greet”.
Soln.:
Isplayfairciphermonoalphabeticcipher
Playfaircipherisnottechnicallymono-alphabetic.Monoalphabeticmeansthateachplaintextlettermappedwithciphertextletterandplayfairisadigraphicsubstitution.Itmapstwoletterpairstotwolatterpairs.
Forplayfair,theorderisunchanged,wejustsubstitutecommondiagraphsforrandomizelookingdigraph.Itisasubstitutioncipher.
Ituserpre-arrangedkey.Soplayfairisaprivatekeycryptosystem.
Constructaplayfairmatrixwiththekey“moonmission”andencryptthemessage “greet”.
Use55matrix
m | o | n | i | s |
a | b | c | d | e |
f | g | h | k | l |
p | q | r | t | u |
v | w | x | y | z |
Themessageis“greet”dividethelatter’sintosetoftwocharacters.
Messagegreet:grexet
Ciphertextis:hq,cz,du
Ex.
Constructaplayfairmatrixwiththekey“occurrence”.Generatetheciphertextforplaintext“talltress”.
Soln.:
Drawmatrix55
o | c | u | r | e |
n | a | b | d | f |
g | h | i/j | k | l |
m | p | q | s | t |
v | w | x | y | z |
Themessageis“Talltrees”dividethelatter’sintothesetoftwocharacter.
MassageTalltrees:Talxltrees
Ciphertextis:pf,i/jz,tz,eo,rt
Ex.
Useplayfairalgorithmwithkey“monarchy”andencryptthetext“jazz”.
Soln.:
Drawmatrix55
m | o | n | a | r |
c | h | y | b | d |
e | f | g | i/j | k |
u | p | q | s | t |
u | v | w | x | z |
Themessageis“Jazz”dividethelatter’sinthesetoftwocharacters.
Message:Jazz
Jazx,zx
Ciphertext:sb,uz,uz
Ex.
Usingplayfaircipherencrypttheplaintext“Why,don’tyou?”.Usethekey“keyword”.
Soln.:
Drawmatrix55
k | e | y | w | o |
r | d | a | b | c |
f | g | h | i/j | l |
m | n | p | q | s |
t | u | v | x | z |
Themessageis“why,don’t,you?”dividethelatter’sintothesetoftwocharacter.
Massage:Why,don’t,you?
Wh,yd,on,’ty,ou
Theciphertext:yi/j,ea,es,vk,ez.
Double transposition encryption uses twice a transposition cipher, usually the first transposition is by columns, and the second by rows.
Example: Encrypt the message DCODE with twice the key KEY. The grid (1) is completed with X and permuted a first time (2)
(1)
| (2)
|
With the message found after the first permutation, then perform a second transposition, but with the rows. The ciphertext is then obtained by reading the grid in rows from left to right and from top to bottom.
Example: The encrypted intermediate message is CDOEDX (3) and the final encrypted message is OECDDX (4):
(3)
| (4)
|
How to decrypt Double Transposition cipher?
Double transposition decryption requires knowing the two permutation keys and the type of transposition for each (row or column)
Example: The crypted message is OECDDX has been transposed with 1 column transposition then with 1 line transposition with two identical keys: KEY.
The encrypted message must get two reversed transposition, in the opposite order of the original order, to get back the plain text.
Example: The grid (1) becomes after inverse permutation in rows (2)
(1)
| (2)
|
Example: The intermediate message CDOECX undergoes a second inverse permutation in columns (3) which gives the original starting grid (4) and the clear message DCODEX
(3)
| (4)
|
OnetimepadinventedbyVernamcalledasVernamcipherthatimprovesthesecurityoversubstitutionandtranspositiontechniques.
Theonetimepadtechniqueusesarandomkeyofthesamelengthofthemessage(aslongasthemessage),sothatthekeyisnotrepeated.Thecasehappenshereissenderisgeneratingnewkeyforeverynewmessagewhilesendingthemessagetothereceivercalledasone-timepad.Thekeyisusedtoencryptanddecryptasinglemessage.
Eachnewmessagerequiresanewkeyofthesamelengthasthenewmessage.Thismethodisunbreakable.Itproducesrandomoutputwithnorelationshiptotheplaintext.Thealgorithmusedareasfollows:
1. Eachalphabetwillbetreatedasnumberfollowing
a=0,b=1…..andsoon.
2. Dothesameforthekeyusedforencrypting.
3. Addboththekeynumbersandplaintextnumbers.
4. Ifthesumisgreaterthan26(0to25),thensubtractitfrom26.
5. Thentheresultnumberistobetranslatedintoalphabetsagain.
ForExampleplaintextmessageisHowAreYou.
Plaintext | H | O | W | A | R | E | Y | O | U |
7 | 14 | 22 | 0 | 17 | 4 | 24 | 14 | 20 | |
Key | n | c | b | t | z | q | a | r | x |
13 | 2 | 1 | 19 | 25 | 16 | 0 | 17 | 23 | |
Total | 20 | 16 | 23 | 19 | 42 | 20 | 24 | 31 | 43 |
Subtract26if>26(0to25) | 20 | 16 | 23 | 19 | 16 | 20 | 24 | 5 | 17 |
Ciphertext | U | Q | X | T | Q | U | Y | F | R |
Sotheciphertextobtainedfortheplaintexthowareyouisuqxtquyfr
Forexample
Thebestexampleofonetimepadisrechargevoucherofanymobilecompany.
Allrechargevoucherhavingdifferentkeyorcodeimprintedonit.Oncethatcodeenteredintomobile,customerwillgettalktimeaccordingtothevouchercost.Ifanothercustomertryingtousesamecodeofvoucherhe/shegetrechargefailuremessage.Thecompanyisregeneratingallkeysorcodeinsuchawaythateveryrechargevoucherhavingnewanduniquecodeonitcalledone-timepad.
Anotherexampleofonetimepadislicensesoftwareorlicensecopyofoperatingsystemandantivirushavingfewkeysavailableaccordingtolicense.Iflicensekeyisof50users?Only50userscanactivatetheirsoftwareafter50usersthenewuserhastobuythenewsoftwarealongwithnewkey.Oncethekeyhasbeenusednobodycanusesamekeyforactivation.
Disadvantages:
1. Largerandomkeycannotbecreated.
2. Keydistributionandgenerationofkeyscanbeproblematic.
3.Intermsofcryptographyitisnotpossibletoimplementonetimepadcommerciallybecausegeneratingnewkeyeverytimeforsendinganewmessagetookmoretimetocompletetransmissionprocess

A codebook is a list of frequently used terms like individual letters, syllables and a codeword for each of them.
They are also called as nomenclators. The designation of the ushers called calamari of a dignitary entering a party, and carried over to those secret books that contained the names of many dignitaries.
Now one simply associates the codes in the words in natural order. The “natural order” of the codes is s, r, q, p, n, m, l, j, h, g, f, d, that is, the reverse of the alphabetic order. Then the syllables are completed by appending -um, -om, -im, -em, and -am.
On the other hand, if the unknown ciphertext 50, then its cleartext is guaranteed to lie between católico and christiandad in any dictionary.
The advantage is that a single list permits an “alphabetic search” both for encryption and decryption. In a two-part codebook, the codes are assigned to the codewords in random order. This provides much higher security, but has the disadvantage of requiring two separate lists for easy encryption and decryption.
An intermediate amount of randomness is used in codebooks that consist of pages of alphabetically ordered words, say numbered from 0 to 99, but where the pages themselves are randomly shuffled.
They are called as one-and-a-half-part codebooks. The German diplomatic codebook 13040, in which the Zimmermann telegram was sent, while the other codebook used in that affair, was of the two part variety.
References:
Text Book :
Information Security Principles & Practices by Mark Stamp, Wiley.
Reference Books :
Introduction to Computer Security by Bishop and Venkatramanayya, Pearson Education.
Cryptography and Network Security : Principles and Practice by Stallings, PHI.