UNIT 2
SYMMETRIC KEY CRYPTO
Instreamcipherkeysandalgorithmsareappliedtoeachbinarydigitinadatastream,onebitatatime,ratherthanencryptingblockofdata(astreamcipheroperatesonplaintextacceptingonlyonebitatatime).
OnetimepadisthebestexampleofstreamcipherinwhicheachbitofplaintextmessageXORwitheachbitofkeytoobtainciphertextmessage.Itisasymmetriccipheroperatesonvaryingtimetransformationindividuallyoneachbit.ThisisshowninFig.
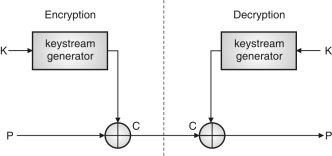
StreamCipher
Thereisakeystreamgeneratorwhichoutputsastreamofbits:k1,k2,k3,...,kiXORwithastreamofplaintextbits,p1,p2,p3,...,pi,toproducethestreamofciphertextbitsc1,c2,c3,.....ci.Broadlyitcanrepresentedasshownbelow
ci = piki ...(2.3.1)
Duringdecryption,theciphertextbitsareXORwithasamekeystreamtorecovertheplaintextbits.
pi = ciki ...(2.3.2)
ThestreamciphersecuritydependsonthesimpleXORandonetimepad.Ifthekeystreamoutputisrandomthat,itwilltakehardertimeforacryptanalysttobreakit.Howeverifitwillkeeponrepeatingsamestreambitsthenitcanresultanattackonthecryptosystem.
Forexample :
Supposewehaveplaintextaspay100inASCII(i.e.textformat).Whenitisconvertedtobinaryvaluesletustakethatitistranslatingas010111001(hypothetically)alsoapplyingXORlogicinencryptionalgorithm.Wecanseeeffectas,
Intextformat | Inbinaryformat |
|
Pay100 | 010111001 | Plaintext |
+ | 100101011 | XORoperationwiththekey |
ZTU91^%D | 11010010 | Ciphertext |
XOR Logic is shown in table below
Input1 | Input2 | Output |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Ratherthandividebitstreamintodiscreteblocksstreamcipherconvertplaintextmessageintociphertextmessagebyencryptingonebitatatime.AtreceiversideusesamekeyandXORlogictoextractplaintextmessage.AnotherinterestingpropertyofXORisthatwhenXORingisdoneusetwicealongwithkey,itproducesbacktheoriginalplaintextdescribedinequationbelow.
pikiki = pi
-It is a stream cipher used in GSM cellular telephone to provide privacy over the air.
-Transmission of GSM is in the form of sequences of bursts. Each bursts has 114 bits are available for information.
-It produces keystream of 114 bits and X-ORed with 114 bit prior to modulation.
- It is initialized with 22 bit frame number.
-Registers are clocked in stop/go way. Clock bit is associated with register.
-The clocking bit gets agree with majority bit if register bit clocks.
-For 64 cycles, registers are initialized to 0.Then secret key of 64 bit is mixed using following equation.
R[0]=R[0] K[i].
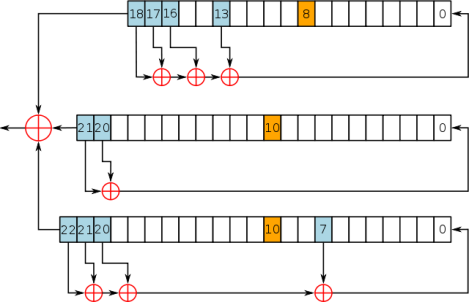 -In similar way 22cycles get added with 22 bits of frame number.
-In similar way 22cycles get added with 22 bits of frame number.
-Following diagram explains working of A5/1
- It is a key algorithms with variable length stream cipher.
- One byte is encrypted at a time only.
- An input given to RC4 is bit generator, generates 8 bit number. This number without knowledge key is unpredictable.
- An produce by RC4 is a key stream. Using X-OR operation the output is combined with plaintext steam cipher.
Key Generation Algorithm
256 byte state vector is initialized with variable length from 1 to 256.
- Key Scheduling Algorithm
The values in S are set values equal to 0 to 255 in ascending order with temporary vector.
If the lengh of the key is equal to 256 byte then k is assigned to T.If not length of K copied from T.
For
i = 0 to 255 do S[i] = i;
T[i] = K[i mod k - len];
T is used to produce to initial permutation.
j = 0;
For
i = 0 to 255 do
{
j = (j + S[i] + T[i])mod 256;
Swap(S[i], S[j]);
}
2. Stream Generation
In this element in S[i] are swapped with another byte in S. When the count reaches to 255, process starts from 0 again.
|
|
|
i, j = 0;
While (true)
i = (i + 1)mod 256;
j = (j + S[i])mod 256;
Swap(S[i], S[j]);
t = (S[i] + S[j])mod 256;
k = S[t];
3. Encrypt using X- Or
In the last step output is encrypted using X-Or.
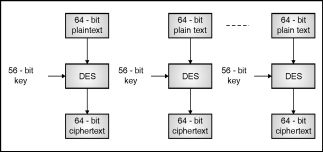
BlockCipherbreakplaintextmessageintofixedblocksandencrypteachblockwithsomekeysize(fixed).Divideeachplaintextmessageintoblockof64,128,256bitsandapplycommonkeysize40,56,64,80,128,168,192and256bitswhichgenerateciphertextmessagesameassizeofplaintextblockoraspersizeofplaintextmessage.
Fig. Shows encryption of 64-bit plain text using block cipher with 56-bit key.
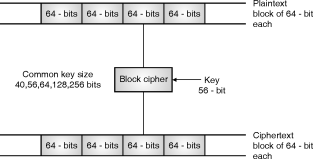
Blockcipher
Blockcipherismainmethodofencryptingtextinwhichkeysandalgorithmareappliedtoblockofdataratherthatindividualbitslikestreamcipher.DataEncryptionStandard(DES)isthebestexampleofblockcipherinwhicheachblockof64-bitgetencryptedusing56-bitkeyandciphertextof64-bitgetgenerated.
Atreceiversidedecryptmessagewithsamekeytogenerateplaintext.
Likeinstreamcipher,blockcipheralsousestheconceptofkeygenerator.BlockcipherareusedinChainingmode,thisisbecauseforrepeatingtextpattern,thesamecipherblockwillbegeneratedwhichcangivecluetocryptanalystregardingwhatistheoriginalplaintexthencechainingmodeisusedforblockciphers.Wewilldiscussconceptofchainingmodeinblockciphermodesofoperation.
Asinchainingmethod,previousblockismixedwithcurrentblocktoavoidrepeatsinpatterns.Blockcipherislittletimeconsumingbutsecurethanstreamciphersogenerallyusedincomputerbasedcryptographicalgorithms.Streamcipherisfasterthanblockcipher.
Feistel cipheris a symmetric structure used in the construction ofblock ciphers.
A cryptographic system based on Feistel cipher structure uses the same algorithm for both encryption and decryption.
The encryption process uses the Feistel structure consisting multiple rounds of processing of the plaintext, each round consisting of a “substitution” step followed by a permutation step.
Feistel Structure is shown in the following illustration –
The input block to each round is divided into two halves that can be denoted as L and R for the left half and the right half.
In each round, the right half of the block, R, goes through unchanged. But the left half, L, goes through an operation that depends on R and the encryption key. First, we apply an encrypting function ‘f’ that takes two input − the key K and R. The function produces the output f(R,K). Then, we XOR the output of the mathematical function with L.
In real implementation of the Feistel Cipher, such as DES, instead of using the whole encryption key during each round, a round-dependent key (a subkey) is derived from the encryption key. This means that each round uses a different key, although all these subkeys are related to the original key.
The permutation step at the end of each round swaps the modified L and unmodified R. Therefore, the L for the next round would be R of the current round. And R for the next round be the output L of the current round.
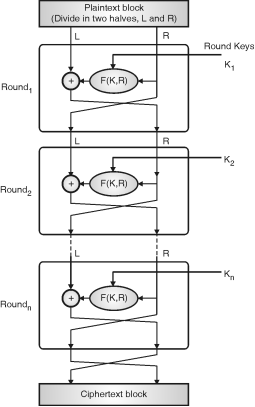
Above substitution and permutation steps form a ‘round’. The number of rounds are specified by the algorithm design.
Once the last round is completed then the two sub blocks, ‘R’ and ‘L’ are concatenated in this order to form the ciphertext block.
DESisblockcipherpublishedbyNationalInstituteofStandardsandTechnology(NIST).
DESwasoriginallydevelopedbyanIBMteamformedinearly1970inresponsetocustomerrequestforamethodtosecuredata.
In1973,NISTpublishedarequestforproposalsforasymmetrickeycryptography.AproposalfromIBM,achangeintheprojectcalledLucifer,wasacceptedasDES.
DESwaspublishedinfederalregisterin1975asadraftoftheFederalInformationProcessingStandard(FIPS).
Thisdraftwasrejectedbecauseofsmallkeylength(56-bits),whichcouldmakeciphertextweakertomanyattacks.
LateronIBMdevelopermentionedthatinternalarchitectureofDESwasdesignedtopreventcryptanalysis.
FinallyNISTpublishedDESinJanuary1977anddefinesDESasthestandardforuseinunclassifiedapplications.
ThedayonwardsDEShasbeenprovenmostwidelyusedsymmetrickeycryptographicalgorithm.
ConceptualViewofDES
Dataencryptionstandardtakes64-bitplaintextasaninputandcreates64-bitciphertexti.e.itencryptsdatainblockofsize64-bitsperblock.
Divideplaintextmessageinto64-bitblockeach.
OR
Thegivenplaintextmessageisdividedintosize64-bitsblockeachandencryptedusing56-bitkeyattheinitiallevel.
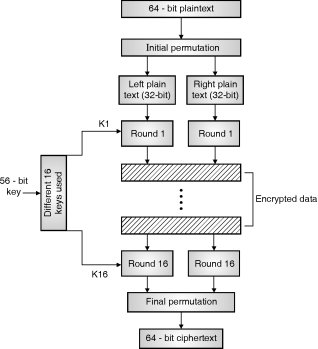
Fig.2.8.1showsconceptualviewofDES.
Atthedecryptionside,DEStakes64-bitciphertextandcreates64-bitplaintextusingsame56-bitkey.
ConceptualviewofDES
DetailStepsofDES
TheprincipleofDESisverysimple.Divideplaintextmessageintoblockofsize64-bitseach,whichisinitialpermutation.
Afterinitialpermutationon64-bitblock,theblockisdividedintotwohalvesof32-bitcalledleftplaintextandrightplaintext.
The left plaintext and right plaintext goes through 16 rounds of encryption process along with 16 different keys for each rounds. After 16 rounds of encryption process left plaintext and right plaintext gets combined and final permutation is performed on these combined blocks.
The final permutation produces 64-bit of ciphertextasshowninFig.
DetailStepsinDES
TripleDESperformsthesameoperationasdoubleDESonlydifferenceisthattripleDESusesthreekeysK1,K2andK3whileencryptingplaintext.
FirstitperformencryptiononplaintextwhichisencryptedusingK1obtainsfirstciphertextagainthisciphertextisencryptedbyusinganotherkeycalledK2whichobtainsthesecondciphertextwhichisagainencryptedusingK3andconvertedintofinalciphertextCp.
Mathematically,DoubleDESisrepresentedas,
 PtEK1(Pt)TEMP=EK1(Pt)EK2(E(K1(P)))
PtEK1(Pt)TEMP=EK1(Pt)EK2(E(K1(P)))
EK3(EK2(EK1(Pt)))
Cp = EK3(EK2(EK1(Pt)))
WherePt = Plaintext
EK1(Pt) = EncryptedplaintextwithKeyK1
TEMP = EK1(Pt)=TemporaryVariabletostore
results
EK2(E(K1(P)))=EncryptedResultsoffirstciphertext
usingK1
EK3(EK2(EK1(Pt)))=EncryptedResultsofsecondstepusingK2
Cp = EK3(EK2(EK1(Pt)))Finalciphertext
encryptedusingK1,K2andK3
DecryptionofTripleDESisreverseofEncryption.
ThefinalciphertextobtainedafterTripleDESencryptionprocessgetdecryptedusingK3whichresultssecondciphertext,secondciphertextdecryptedusingK2whichresultsfirstciphertext,firstciphertextagaindecryptedusingK1whichgeneratetheoriginalplaintextPt.
TodecrypttheciphertextCpandobtaintheplaintextPt,weneedtoperformfollowingoperation.
Pt = DK3(DK2(DK1(Cp)))
DESusedthethreekeysandotherusesthetwokeys,Therearetwoways:
1. TripleDESwithtwokeys
2. TripleDESwiththethreekeys
TripleDESwithTwoKeys
TripleDESusethethreekeysbecauseofthatitishighlysecure.
Wecanshowitintheformofequationisasfollows:
Cp = EK3(EK2(EK1(Pt)))
WhentripleDESuseditrequirethethreekeysitisalsorequire563=168bitsforkeyisthedrawbackoftheTripleDES.
Whenitisdonepractically,itisdifficult.
AworkaroundsuggestedbyTuchmantheusesonlyjustatwokeyforthetripleDES.
i.e.algorithmisasfollows:
1. Theplaintextisencryptwiththek1.ThuswegetEK3(Pt)
2. AfterthatwhateveroutputcomesdecryptedthatwithkeyK2.Thus,wegettheK2(EK(Pt))
3. Attheend,encrypttheoutputofthestep2andagainencryptwiththekeyK1.Thusweget,
EK1(DK2(EK1(Pt)))
ThisshownintheFig.
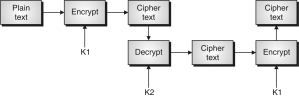
WhenwedothedecryptionontheciphertextCpwegettheplaintextPtorthatweneedtoperformtheoperation.
Pt = DK1(EK2(DK1(Cp)))
Here,thereisnospecialmeaningtothestep2ofthedecryption.ItisonlyunderstandingisthatitallowstripleDESworkwithtwokeys,ratherthreekeys.
ThisprocedureisknownastheEncryptDecryptEncrypt(EDE)mode.
TripleDESwiththeThreeKeys
ThediagramshowsyoutheactualworkingofthetripleDES.
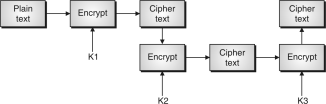
InFig.,theplaintextPisfirstencryptedusingtheK1,andthenencryptedwiththeK2,andattheendthirdK3.TheK1,K2,K3aretotallydifferentfromtheeachother.
ThePGPandS/MIMEapplicationareusedinthetripleDES.
Usingthedecryptionmethod,weconvertthecipherCpintotheplaintextPt.toperform,Thisoperationweuse
Pt = DK3(DK2(DK1(Cp)))
IntroductiontoAES
TheAdvancedEncryptionStandard(AESAlgorithm)isaSymmetrickeycryptographicalgorithmpublishedbyNationalInstituteforStandardsandTechnology(NIST)inDecember2001.
ThealgorithmwasproposedbyRijndaelthereasonalsocalledRijndaelencryptionalgorithm.Advanceencryptionstandardisareplacementofdataencryptionstandard.
SilentFeaturesofAES
TheAESalgorithmisasubsetoftheRijndaelalgorithmandisablockcipher,meaningthatitoperatesonaninputblockofdataofaknownsizeandoutputsablockofdatawhichisthesamesize.AninputkeyisalsorequiredasinputtotheAESalgorithm.
Itallowsthedatalength(plaintextsize)of128,192and256bits,andsupportingthreedifferentkeylengths,128,192,and256bits.
TheAESalgorithmisasymmetrickeyalgorithmwhichmeansthesamekeyisusedtobothencryptanddecryptamessage.Also,theciphertextproducedbytheAESalgorithmisthesamesizeastheplaintextmessage.
AESconsistsofmultipleroundsforprocessingdifferentkeybitslike10roundsforprocessing128-bitkeys,12roundsforprocessing192-bitkeys,and14roundsforprocessing256-bitkeys.
AESEncryption and Decryption Process
- Theplaintextgivenisdividedinto128-bitblockasconsistingofa4×4matrixofbytes.
Therefore,thefirstfourbytesofa128-bitinputblockoccupythefirstcolumninthe4×4matrixofbytes.Thenextfourbytesoccupythesecondcolumn,andsoon.AESoperatesona4× 4 column-major order matrix of bytes; called as statearrayshowninFig. AESalsohasthenotionofaword.
Awordconsistsoffourbytesthatis32bits.TheoverallstructureofAESencryption and decryptionprocessisshownin Fig.
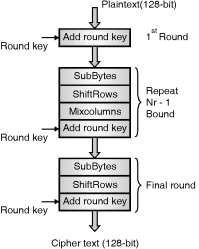
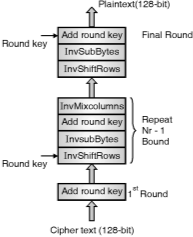
AESEncryptionandDecryptionprocess
Thenumberofroundsare10,isforthecasewhentheencryptionkeyis128bitlong.(Asmentionedearlier,thenumberofroundsis12whenthekeyis192bitsand14whenthekeyis256.)
Beforeanyround-basedprocessingforencryptioncanbegineachbyteofthestate(plaintext)iscombinedwiththeroundkeyusingbitwiseXORoperation.Nrstandsfornumberofrounds.
AESdivideplaintextinto16byte(128-bit)blocks,andtreatseachblockasa44Statearray.Itthenperformsfouroperationsineachroundconsistsofseveralprocessingstepslikesubstitutionstep,arow-wisepermutationstep,acolumn-wisemixingstep,andtheadditionoftheroundkey.Exceptforthelastroundineachcase,allotherroundsareidentical.FinalRounddoesn’thave(MixColumns)itincludesonlySubBytes,ShiftRowsandAddRoundKey.
TheprocessoftransformingtheciphertextbackintotheoriginalplaintextusingsameencryptionkeyiscalledasdecryptionprocessofAES,duringdecryptionprocessthesetofroundsarereversed.
DetailStepsforAESEncryption
Forencryption,eachroundconsistsofthefollowingfoursteps:
 Steps for AES Encryption
Steps for AES Encryption
1. TheSubBytestep/Substitutebyte
SubBytes()consistsofreplacementofeachbyteusingafixedS-boxlookuptableasshowninFig.toachievenon-linearityintothe44statearray(16byte).ItperformsroughlythesamefunctionastheS-BOXinDES.
Itoperatesoneachbyteinthestateandperformsanon-linearsubstitutionintheGaliosFiledGF(28)field,whichiswhatmakesAESanon-linearcryptographicsystem.
|
| Y |
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | a | b | c | d | e | F |
X | 0 | 63 | 7c | 77 | 7b | F2 | 6b | 6f | C5 | 30 | 1 | 67 | 2b | Fe | D7 | Ab | 76 |
1 | Ca | 82 | C9 | 7d | Fa | 59 | 47 | F0 | Ad | D4 | A2 | Af | 9c | A4 | 72 | C0 | |
2 | b7 | Fd | 93 | 26 | 36 | 3f | F7 | Cc | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 | |
3 | 4 | C7 | 23 | C3 | 18 | 96 | 5 | 9a | 7 | 12 | 80 | E2 | Eb | 27 | B2 | 75 | |
4 | 9 | 83 | 2c | 1a | 1b | 6e | 5a | A0 | 52 | 3b | D6 | B3 | 29 | E3 | 2f | 84 | |
5 | 53 | D1 | 0 | Ed | 20 | Fc | B1 | 5b | 6a | Cb | Be | 39 | 4a | 4c | 58 | Cf | |
6 | D0 | Ef | Aa | Fb | 43 | 4d | 33 | 85 | 45 | F9 | 2 | 7f | 50 | 3c | 9f | A8 | |
7 | 51 | A3 | 40 | 8f | 92 | 9d | 38 | F5 | Bc | B6 | Da | 21 | 10 | Ff | F3 | D2 | |
8 | Cd | 0c | 13 | Ec | 5f | 97 | 44 | 17 | C4 | A7 | 7e | 3d | 64 | 5d | 19 | 73 | |
9 | 60 | 81 | 4f | Dc | 22 | 2a | 90 | 88 | 46 | Ee | B8 | 14 | Be | 5e | 0b | Db | |
a | E0 | 32 | 3a | 0a | 49 | 6 | 24 | 5c | C2 | D3 | Ac | 62 | 91 | 95 | E4 | 79 | |
b | E7 | C8 | 37 | 6d | 8b | D5 | 4e | A9 | 6c | 56 | F4 | Ea | 65 | 7a | Ae | 8 | |
c | Ba | 78 | 25 | 2e | 1c | A6 | B4 | C6 | E8 | Dd | 74 | 1f | 4b | Bd | 8b | 8a | |
d | 70 | 3e | B5 | 66 | 48 | 3 | F6 | 0e | 61 | 35 | 57 | B9 | 86 | C1 | 1d | 9e | |
e | E1 | F8 | 98 | 11 | 69 | D9 | 8e | 94 | 9b | 1e | 87 | E9 | Ce | 55 | 28 | Df | |
f | 8c | A1 | 89 | 0d | Bf | E6 | 42 | 68 | 41 | 99 | 2d | 0f | B0 | 54 | Bb | 16 |
S-BoxLookuptableforSubBytes
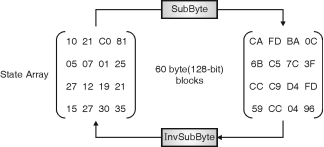
SubBytetransformation
Fig.showsthestatetransformationusingSubBytestechniquesandifapplyreversecalledasInvSubBytestransformationwhichwillcreateoriginalvalues.Foreverysametwobytevaluetheresultingtransformationisalsosame.ItalsoshowsthattheInvSubBytestransformationcreatestheoriginalone.
Notethatifthetwobyteshavethesamevalues,theirtransformationisalsothesame.ThecorrespondingsubstitutionstepusedduringdecryptioniscalledInvSubBytes.
2. ShiftRows
TheoutputoftheSubBytetransformationisinputtotheShiftRowstransformationwhichconsistsofrotationofeachbyteofthestatearrayintheorderofarowofdatamatrix(rotationofrowbytepositionsaredoneinthisstep).
Eachbyteofthefirstrowremainsunchanged.Eachbyteofthesecondrowisrotateoveronebytetotheleftposition.Similarlythethirdandfourthrowsarealsorotatedleftbytwoandthreepositionasshownin
Fig.
ThecorrespondingtransformationduringdecryptionprocessiscalledInverseshiftrowtransformation(InvShiftRows).
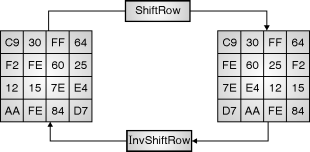
ShiftRowstransformation
3. MixColumns
MixColumnsperformsoperationonthestatearrayobtainedfromShiftRowscolumn-by-columnandeachcolumnismultipliedwithrowofafixedmatrix.Thissteptakesfourbytesasaninputandproducesoutputsoffourbytes(eachinputbyteaffectstheoutputbytes).
ThefournumbersofstatearraysoffirstcolumnaremodulomultipliedinRijandeal’sGaliosFiled(GF)byagivenmatrixasshowninFig.2.11.5.InAESMixColumnstepalongwithShiftRowsareprimarysourceforprovidingcompletediffusiontothecipherproduced.
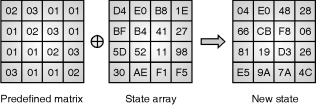
MixColumnstransformation
FromFig.2.11.5onthelefthandside,therowoftheleftmostmatrixismultiplywithcolumnofstatearray(XORoperations)whichproducesthenewstate.Performthesameoperationonallcolumnswhichprovidesdiffusion(mixingdatawithincolumns).
The4bytesofeachcolumnintheStatearetreatedasa4-bytenumberandtransformedtoanother4-bytenumberviafinitefieldmathematics(modulomultipliedinRijndael’sGaloisFiledbyagivenmatrix)asshown.MixColumnsstepisprimarysourceofdiffusioninAES.
4. AddRoundKey
IntheAddRoundKeystep,theRoundkeyonegeneratedusingRijndael'skeyscheduleiscombinedwiththenewstateobtainedfromMixColumnstransformationstate.
TheroundkeyisaddedbycombiningeachbyteofthestatearrayusingbitwiseXORoperations.Theactual‘encryption’isperformedintheAddRoundKey()function,wheneachbyteofstatearrayisXORedwiththeroundkeyasshowninFig.2.11.6
04 | E0 | 48 | 28 |
| A0 | 88 | 23 | 2A |
| A4 | 68 | 6B | 02 |
66 | CB | F8 | 06 |
| FA | 54 | A3 | 6C |
| 9C | 9F | 5B | 6A |
81 | 19 | D3 | 26 |
| FE | 2C | 39 | 76 |
| 7F | 35 | EA | 50 |
E5 | 9A | 7A | 4C |
| 17 | B1 | 39 | 05 |
| F2 | 2B | 43 | 49 |
AddRoundKey
ThesameprocessofAddRoundKeyisappliedfornineroundsi.eRepeatSubByte,ShiftRows,MixColumnsstepandXORwithRoundkey9moretimes.
Exceptforthelastroundineachcase,allotherroundsareidentical.FinalRounddoesn’thaveMixColumnsstepitincludesonlySubBytes,ShiftRowsandRoundKey.
FinallyanoutputciphertextwillobtainafterperformingdetailstepsofAES.Asetofreverseroundsareapplied(i.e.InvShiftRows,InvSubBytes,AddRoundKeyandInvMixcolumns)totransformciphertextbackintotheoriginalplaintextusingthesameencryptionkeycalledDecryptionprocessofAESasshowninFig.
AESDecryption
DecryptionoccursthroughthefunctionAddRoundKey(),plustheinverseAESfunctionsInvShiftRows(),InvSubBytes(),InvMixColumns()andAddRoundKey()doesnotrequireaninversefunction,asitsimplyXORsthestatewiththesubkey(XORencryptswhenappliedonce,anddecryptswhenappliedagain).
Sr.No. | DES | AES |
1. | Dataencryptionstandardtakes64-bitplaintextasainputandcreates64-bitCiphertexti.e.itencryptsdatainblockofsize64-bitsperblock. | Itallowsthedatalength(plaintextsize)of128,192and256bits. |
2. | InDESplaintextmessageisdividedintosize64-bitsblockeachandencryptedusing56-bitkeyattheinitiallevel. | AESdivideplaintextinto16byte(128-bit)blocks,andtreatseachblockasa44Statearrayandsupportingthreedifferentkeylengths,128,192,and256bits.
|
3. | Theleftplaintextandrightplaintextgoesthrough16roundsofencryptionprocessalongwith16differentkeysforeachrounds. | Thenumberofroundsare10,isforthecasewhentheencryptionkeyis128bitlong.(Asmentionedearlier,thenumberofroundsis12whenthekeyis192bitsand14whenthekeyis256.) |
4. | DESuses56-bitkeyssothatthereare256possiblekeycombinationswhichisroughlyequalto7.21016keysrequiredtobreakDEScipher. | AESisstrongerthanDESbecauseofkeysizevaryfromroundtoround. |
5. | DifferentversionsofDESaredoubleDESandtripleDESisadded. | AESdoesn’thaveanyfutureversion. |
6. | DESdoesn’tuseMixColumn,ShiftRowsmethodduringencryptionanddecryptionprocess | AESusesMixColumn,ShiftRowsmethodduringencryptionanddecryptionprocess |
7. | DES,doubleDESandTripleDES(168-bitkey)arevulnerabletobruteforceattacks. | AESalsoarevulnerabletobruteforceattacks. |
References:
Text Book :
Information Security Principles & Practices by Mark Stamp, Wiley.
Reference Books :
Introduction to Computer Security by Bishop and Venkatramanayya, Pearson Education.
Cryptography and Network Security : Principles and Practice by Stallings, PHI.