Unit 5
Mathematics Preliminaries
5Stability analysis using Nyquist Path :-
Encircled : A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption :-
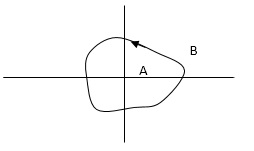
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Further more when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed :-
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
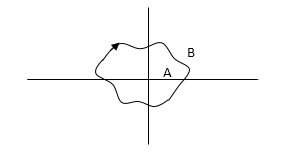
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosures :-
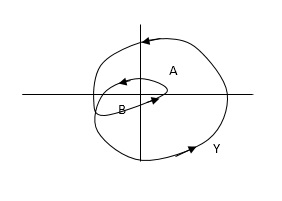For A line is cut once
For B line is cut twice
As it’s overlapping but 2 times in
Same direction
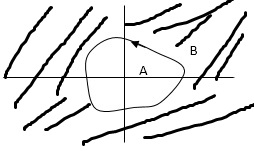
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
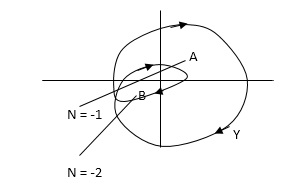
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
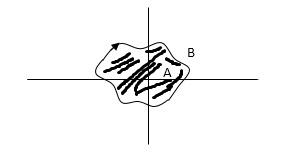
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
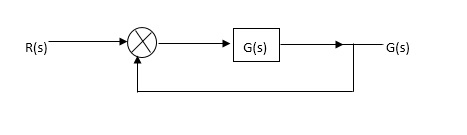
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Inference:-
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
Inference :-
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
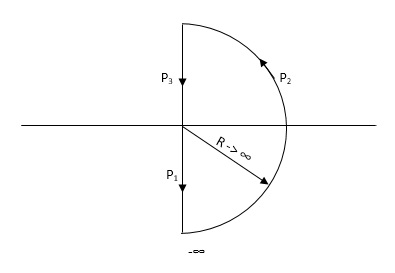
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
- Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important :-
# Open loop System(stable) :- When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable) :-Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Generalized Point :-
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
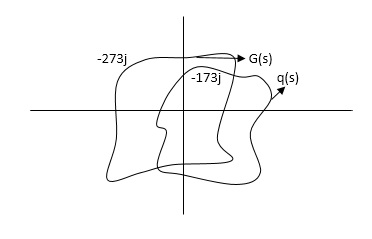
G(S) given then q(S) shift to right side.
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol:- N = Z – P ( No pole of right half of S plane P = 0 )
P = 0, N = Z
NYQUIST PATH :-
P1 = W – (0 to - ∞)
P2 = ϴ( - π/2 to 0 to π/2 )
P3 = W(+∞ to 0)
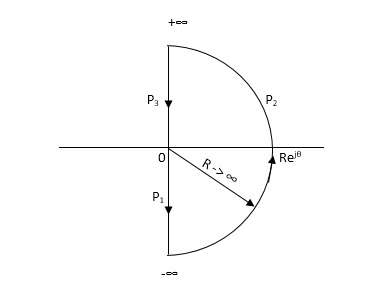
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1 :- W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2 :-
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3 :-
W = -∞ to 0
M = 1/√1+W2 , φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 6
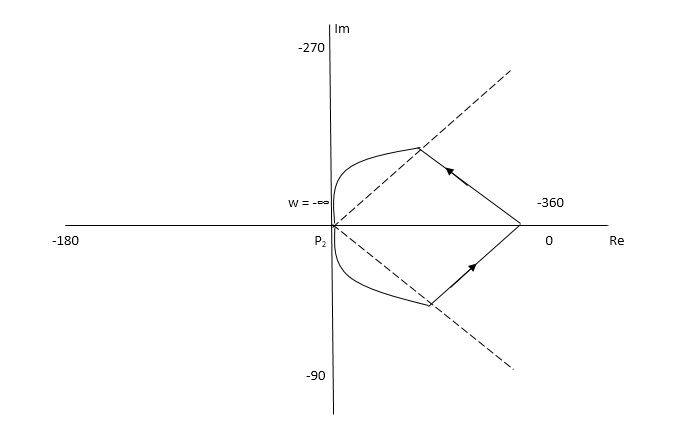
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln :- N = Z – P , P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)
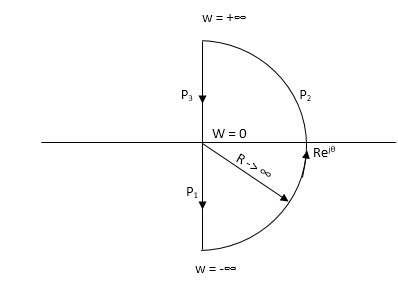
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2 :ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 7. From plot N=0, Z=0, system stable.
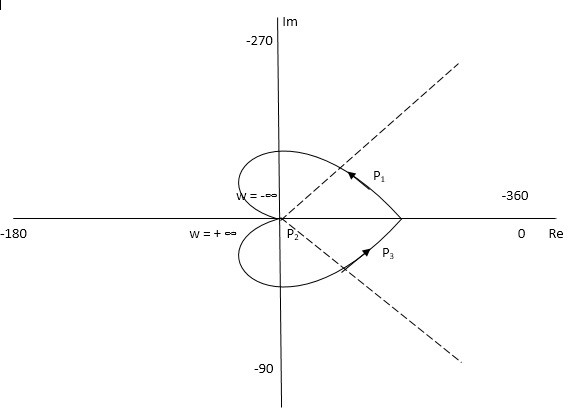
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1 : Not including poles at origin in the Nyquist Path.
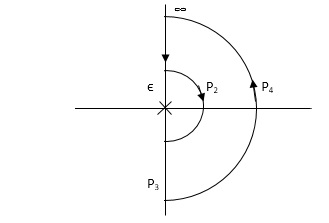
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π ]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0
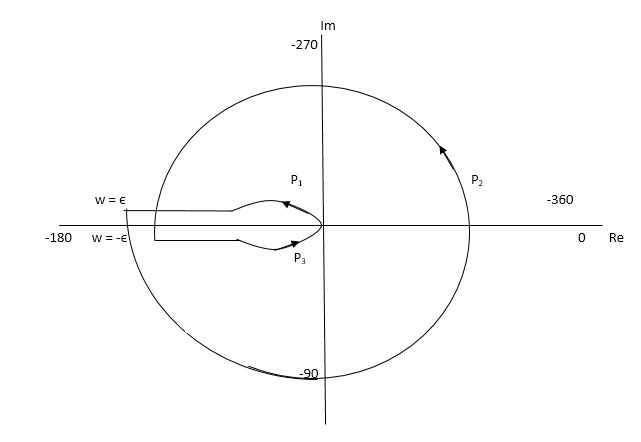
But from plot shown in fig 8(a). It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
PART 2 Including poles at origin in the Nyquist Path.
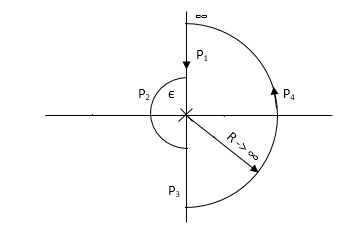
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3( mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
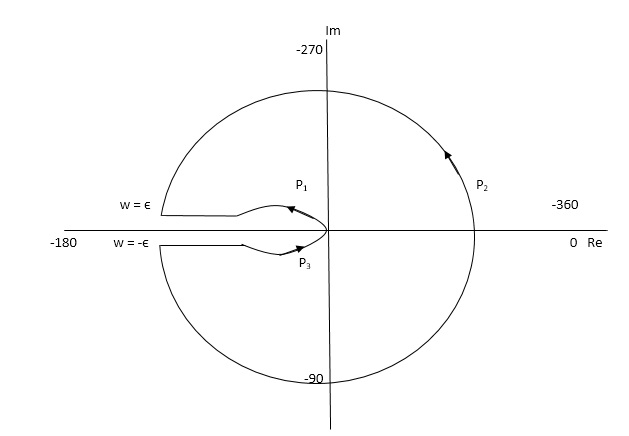
The plot is shown in fig. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path.(P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE : The sign convention for angles is shown
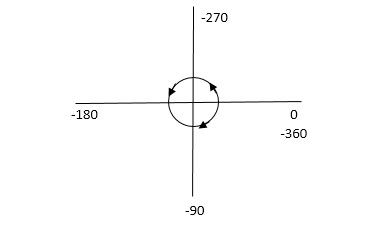
Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
Reference Books :
- Modern Control Engineering by K.Ogata, Pearson Education.
2. Control Engineering by Kuo.
Unit 5
Mathematics Preliminaries
5Stability analysis using Nyquist Path :-
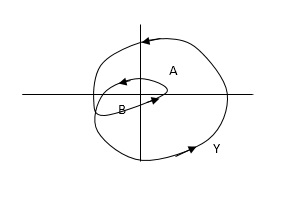
Encircled : A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption :-
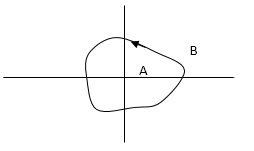
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Further more when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed :-
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
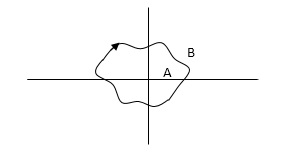
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are
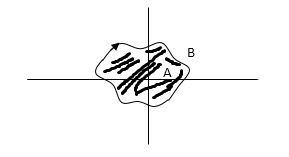
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosures :-
For A line is cut once
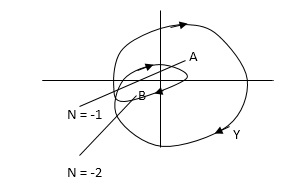
For B line is cut twice
As it’s overlapping but 2 times in
Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
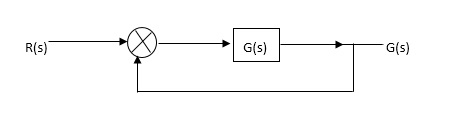
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Inference:-
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
Inference :-
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
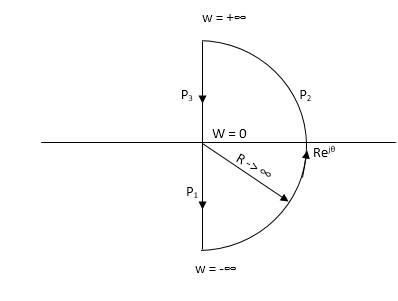
Consider a contour, which covers the entire right half of S-plane.
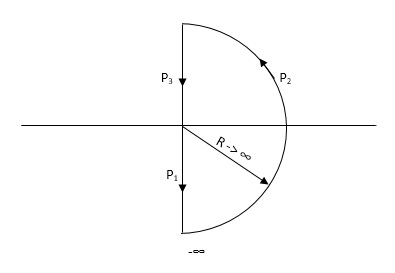
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
- Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important :-
# Open loop System(stable) :- When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable) :-Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Generalized Point :-
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
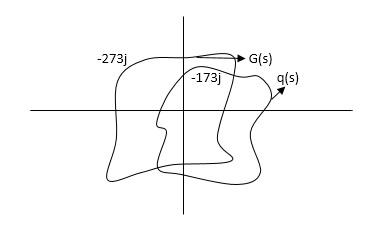
G(S) given then q(S) shift to right side.
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol:- N = Z – P ( No pole of right half of S plane P = 0 )
P = 0, N = Z
NYQUIST PATH :-
P1 = W – (0 to - ∞)
P2 = ϴ( - π/2 to 0 to π/2 )
P3 = W(+∞ to 0)
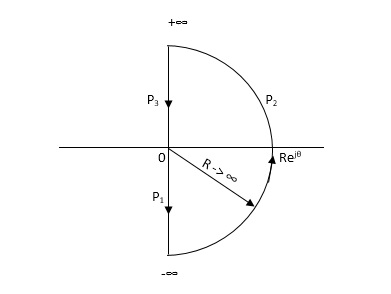
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1 :- W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2 :-
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3 :-
W = -∞ to 0
M = 1/√1+W2 , φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 6
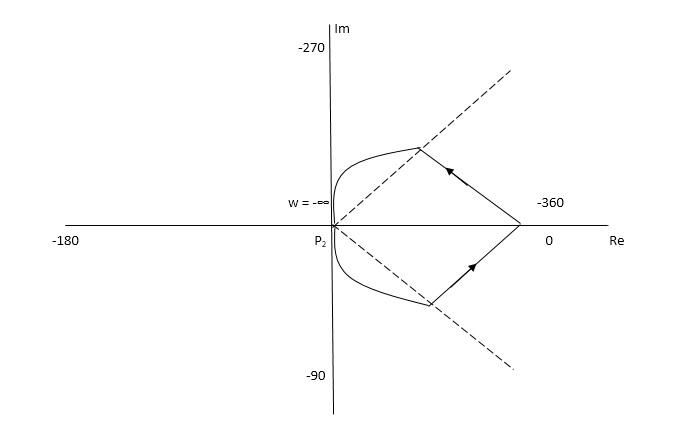
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
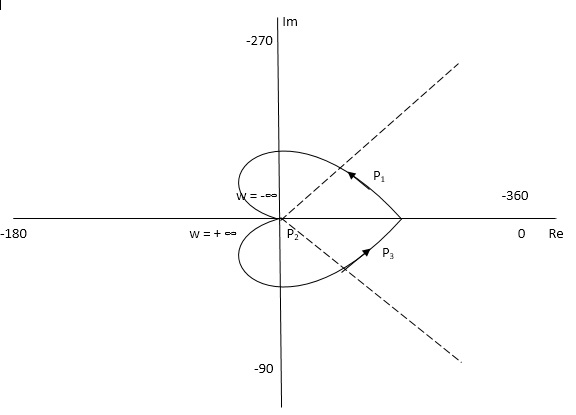
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln :- N = Z – P , P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2 :ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 7. From plot N=0, Z=0, system stable.
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1 : Not including poles at origin in the Nyquist Path.
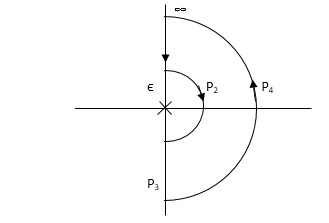
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π ]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0
But from plot shown in fig 8(a). It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
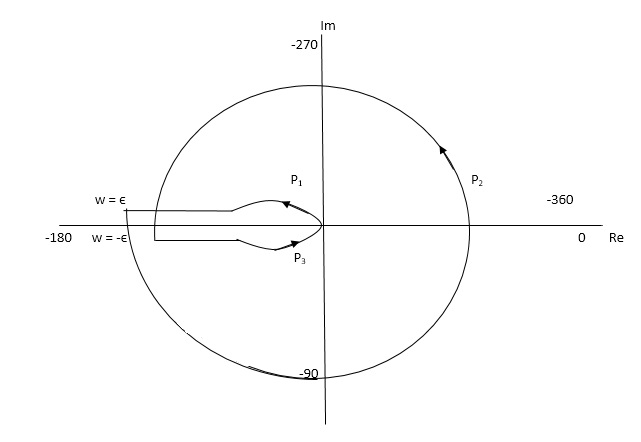
PART 2 Including poles at origin in the Nyquist Path.
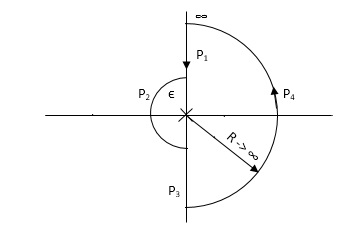
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3( mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
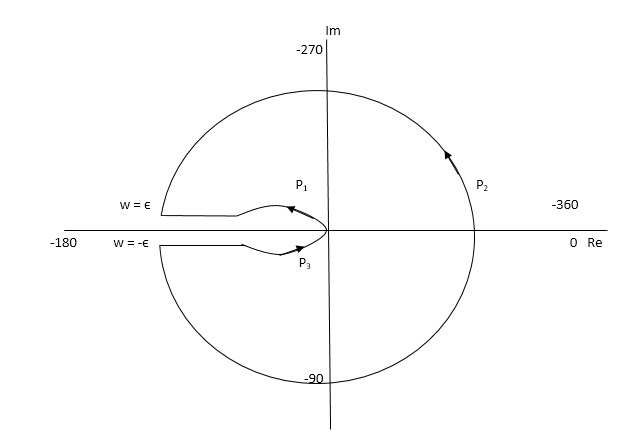
The plot is shown in fig. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path.(P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE : The sign convention for angles is shown
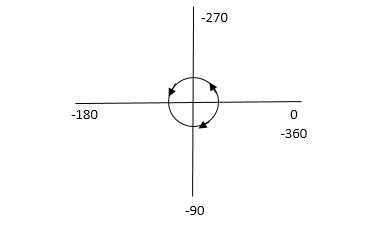
Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
Reference Books :
- Modern Control Engineering by K.Ogata, Pearson Education.
2. Control Engineering by Kuo.
