Unit 3
Fourier Series
A signal is said to be periodic if it satisfies the condition x (t) = x (t + T) or x (n) = x (n + N).
Where T = fundamental time period,
ω0= fundamental frequency = 2π/T
There are two basic periodic signals:
x(t) = cos wot (sinusoidal)
x(t) = e jwot (complex exponential)
These two signals are periodic with period T=2π/ω0
A set of harmonically related complex exponentials can be represented as ɸk(t)
ɸk(t) = { e jkwot} = { e jk(2π/T)t} where k=0,±1,±2,±3,………………(1)
All these signals are periodic with period T.
According to orthogonal signal space approximation of a function f(x) with n mutually orthogonal functions is given by
x(t) = 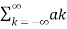 e jkwot ……………………………………………….(2)
e jkwot ……………………………………………….(2)
=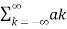 k ejkwot
k ejkwot
Where ak= Fourier coefficient = coefficient of approximation.
This signal x(t) is also periodic with period T.
Equation 2 represents the Fourier series representation of periodic signal x(t).
The term k = 0 is constant.
The term k=±1 having fundamental frequency ω0, is called as 1st harmonics.
The term k=±2 having fundamental frequency 2ω0, is called as 2nd harmonics, and so on...
The term k=±n having fundamental frequency nω0, is called as nth harmonics.
Deriving Fourier Coefficient
We know that x(t) =  e jkwot ------------------------(1)
e jkwot ------------------------(1)
Multiply e-jnwot on both sides we get
x(t) e -jnwot = 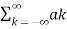 e jkwot . e- jnwot
e jkwot . e- jnwot
Consider integral on both sides we get
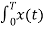 e jkwot dt =
e jkwot dt = 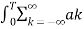 e jkwot . e- jnwot
e jkwot . e- jnwot
= 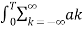 e j(k-n)wot dt
e j(k-n)wot dt
= 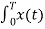 e jkwot dt =
e jkwot dt = 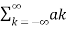
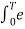 j(k-n)wot dt --------------------------(2)
j(k-n)wot dt --------------------------(2)
By Eulers formula
 j(k-n)wot dt =
j(k-n)wot dt =  wo dt + j
wo dt + j 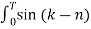 wo dt
wo dt
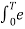 j(k-n)wot dt = { T k=n
j(k-n)wot dt = { T k=n
0 k  n
n
Hence in equation(2) the integral is zero for all values of k except at k=n. Put k=n is equation 2
= 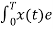 j(k-n)wot dt = anT
j(k-n)wot dt = anT
=an = 1/T 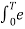 -jnwot
-jnwot
Replace n by k we get
= ak = 1/T  -jkwot dt
-jkwot dt
x(t) =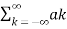 e j(k-n) wot
e j(k-n) wot
Where ak = 1/T 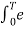 -jkwot dt
-jkwot dt
Key Take-Aways:
- Definition of Fourier series
- Its derivation for periodic continuous-time signal
The Dirichlet condition for the existence of the Fourier series is:
- f(x) is single-valued with a finite number of discontinuities in [-L, L]
- f(x) has finite number of extrema in[-L,L]
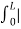 f(x)| dx exists
f(x)| dx exists 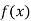 is 2L periodic
is 2L periodic
Key Take-Aways:
- The Dirichlet condition for Fourier series existence
Consider f(x) belong to the vector space spanned by cos[nπx/L] n=1,2,3…….
And sin [nπx/L] n=1,2,3
Cos[nπx/L] = cos[nπ(x+2L)/L]
Sin[nπx/L] = sin [ nπ(x+2L/L)]
This means that any function built from a linear combination
g(x) = ao + 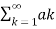 cos[kπx/L] + bk sin [kπx/L]
cos[kπx/L] + bk sin [kπx/L]
Will also be periodic.
These basis functions are orthogonal for m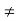 n
n
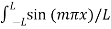 sin(nπx/L)
sin(nπx/L)
= ½ 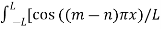 - cos((m+n)πx/L)] dx
- cos((m+n)πx/L)] dx
=0
Because (m+n)=0 and m-n 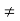 0
0
So if m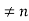 < sin mπx/L | sin nπx/L > =0
< sin mπx/L | sin nπx/L > =0
And if m=n
<sin mπx/L| sin mπx/L>
= 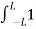 - cos2πmx/L)] dx
- cos2πmx/L)] dx
=1/2 [ x – sin[2πmx/L]/2πm/L |-L L =L
Can also show that
<cos mπx/L | sin nπx/L> = 0 for all m,n
<cos mπx/L | cos nπx/L> = L δmn
So the basis
Cos[nπx/L] n=0,1,2…….. And sin [nπx/L] n=1,2,3 is orthogonal on[-L,L]
Key Takeaways:
- Definition of orthogonality
- Condition for orthogonality
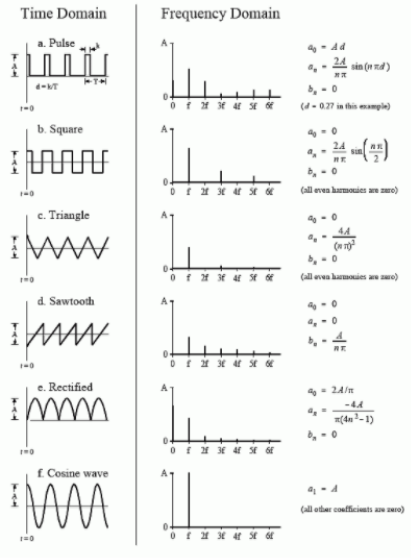
Figure 1. Time and Frequency domain representation of various signals
Key Take-Aways:
- Representation of various signals like square, triangle, and so on in time domain
- Representation of various signals in the frequency domain.
The Fourier series is a representation of the function in terms of sine and cosine functions as follows:
x(t)= a0 + 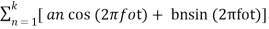
Here the an and bn are coefficients defined as integrals in terms of the specific x(t).
The cosine term an cos(2nf0 t) and a sine term bn sin(2pnf0 t) (of the same frequency nf0 ) may be viewed as a single cosine waveform of frequency nf0 :
An cos(2πnf0 t) + bn sin(2πnf0 t) = An cos(2πnf0 t + ɸn )
Where the amplitude
An= √ an 2 + b n 2 and the phase angle ɸn = - tan-1 (bn/an)
Cos(2πnf0 t + ɸn ) = cos(ɸn) cos (2πfot) – sin(ɸn) sin(2πfnt)
Because ɸn = - tan-1 (bn/an) which implies that sin(ɸn) = -bn/ √ an2 + bn 2
Cos(ɸn) = an/ √ an2 + bn 2
Thus,
x(t) = ao +  n cos (2πfot + ɸn)
n cos (2πfot + ɸn)
In any Fourier series for a real periodic function, each pair of an and bn coefficients leads to a single cosine with frequency nf0. The phase ɸn of each cosine may be different, just as the non-negative amplitudes An are generally different. The phase relationships are important because they correspond to having different amounts of "time shifts" or "delays" for each of the sinusoidal waveforms relative to a zero-phase waveform.
Illustrating the importance of phase, in the figure below are shown two waveforms
x1 (t) = cos(2π2f 0t) – 0.5cos(2π3f 0 t + π/4)
=cos(2π2f 0 t) + 0.5cos(2π3f 0 t + 5π/4) and
x2 (t) = cos(2π2f0t) – 0.5cos(2π3f0t+π) with f0= 0.5 Hz.
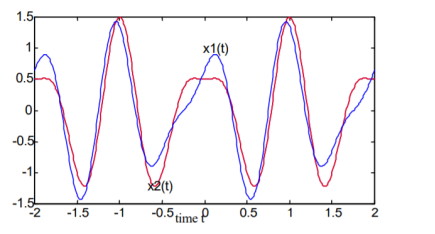
Figure 2. Amplitude and Phase
The amplitude spectrum refers only to the amplitudes An. It may be plotted as a function of n. Similarly, the phase spectrum is the phase fn as a function of n.
Key Take-Aways:
- Fourier series periodic function
- Its representation in time and frequency domain
FS representation of CT signals using trigonometric
Any arbitrary periodic function x(t) with fundamental period To can be expressed as follows
x(t) = ao + 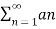 cos nwot + bn sin nwot ----------------------------------(1)
cos nwot + bn sin nwot ----------------------------------(1)
This is referred to as the trigonometric Fourier series representation of the signal x(t). Here wo = 2π/To is the fundamental frequency and the co-efficient ao, an and bn are referred to as the trigonometric continuous-time Fourier series co-efficient. The coefficient is calculated as
Ao = 1/To 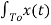 dt
dt
An = 2/To 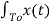 cos nwot dt
cos nwot dt
Bn = 2/To 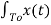 sin nwot dt
sin nwot dt
From the equations, it is clear that co-efficient ao represents the average or mean value of signal x(t).
In these formulas the limits of integration are either (-To/2, +To/2 ) or (0 to To). In general, the limit of integration is any period of the signal and so the limits can be from (t1to t2 +To) where t1 is any time instant.
Exponential Fourier series
The exponential Fourier series is another form of Fourier series. Using Euler’s identity we can write
An cos(Ω0nt +  n ) = An [ ej(Ω0nt +
n ) = An [ ej(Ω0nt + 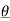 n) –e -j(Ω0nt +
n) –e -j(Ω0nt + 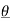 n)]
n)]
2
x(t) = A0 + 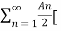 ej(Ω0nt +
ej(Ω0nt + 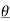 n) –e- j(Ω0nt +
n) –e- j(Ω0nt + 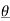 n)]
n)]
= A0 + 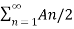 e j(Ωont) ejƟn – e - j(Ωont) e j(-Ɵn)
e j(Ωont) ejƟn – e - j(Ωont) e j(-Ɵn)
= A0 + 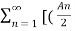 ej
ej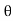 n ) ej(Ω0nt ) + (An/2 e-j
n ) ej(Ω0nt ) + (An/2 e-j 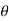 n ) e- j(Ω0t ) ] -------- (1)
n ) e- j(Ω0t ) ] -------- (1)
Let n=-k
x(t) = A0 + 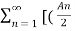 ejƟn ) ej(Ω0nt ] +
ejƟn ) ej(Ω0nt ] + 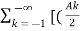 e j Ɵk ) e j(Ω0kt ) ------- (2)
e j Ɵk ) e j(Ω0kt ) ------- (2)
Comparing (1) and (2) we get
An = Ak (-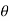 n ) =
n ) = 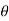 k n>0 k<0-------------------(3)
k n>0 k<0-------------------(3)
Let us define c0 = A0 ; cn =An/2 ej Ɵn for n>0
By changing the index from k to n and combining into one equation we get
x(t) = A0 +  e j ) ej(Ω0nt) +
e j ) ej(Ω0nt) + 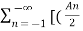 ej
ej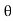 n) ej(Ω0nt)]
n) ej(Ω0nt)]
x(t) = 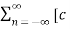 n ej(Ω0nt) ]
n ej(Ω0nt) ]
The above series is known as the Exponential Fourier Series.
To develop the coefficients of the exponential Fourier series
We know that
x(t) = 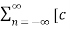 n ej(Ω0nt) ] where Ω0 = 2π/T
n ej(Ω0nt) ] where Ω0 = 2π/T
Multiply e-jk Ω0 t and integrate over one period. Then
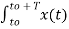 e-jk Ω0 t dt =
e-jk Ω0 t dt =  cn ej(Ω0nt) ] e-jk Ω0 t dt
cn ej(Ω0nt) ] e-jk Ω0 t dt
= 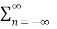 cn
cn 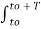 ej(Ω0nt) e-jk Ω0 t dt
ej(Ω0nt) e-jk Ω0 t dt
Substituting the relation 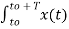 e-jk Ω0 t dt = 0 for k ≠n and T when k=n
e-jk Ω0 t dt = 0 for k ≠n and T when k=n
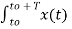 e-jk Ω0 t dt = T ck
e-jk Ω0 t dt = T ck
Therefore
Ck = 1/T 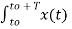 e-jk Ω0 t dt
e-jk Ω0 t dt
Or
Cn = 1/T 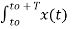 e-jk Ω0 t dt
e-jk Ω0 t dt
Where Cn is the Fourier series coefficients of exponential Fourier series.
Compute the Fourier series f(t) where f(t) is the square wave with period 2π which is defined over one period by
f(t) = { -1 for -π  t
t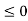
1 for 0 <π
<π
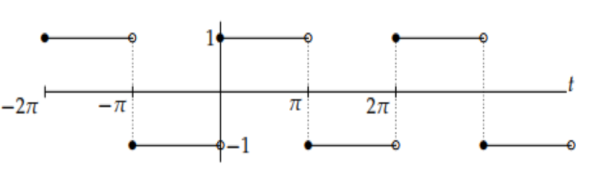
Figure 3. Square waveform
f(t) = ao/2 + 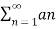 cos(nt) + bn sin(nt))
cos(nt) + bn sin(nt))
Where
Ao =1/π 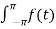 dt an = 1/π
dt an = 1/π 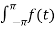 cos nt dt bn =1/π
cos nt dt bn =1/π 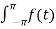 cos nt dt
cos nt dt
By applying these formulas to the above waveform we have to split the integrals into two pieces corresponding to where f(t) is +1 and where it is -1.
Thus for n 0; an = -sin (nt)/nπ| 0 -π + sin(nt) /n
0; an = -sin (nt)/nπ| 0 -π + sin(nt) /n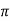 | π 0 =0
| π 0 =0
For n=0 ao = 1/π  dt =0
dt =0
Likewise
Bn = 1/π sin(nt) dt = 1/ π
sin(nt) dt = 1/ π 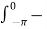 sin(nt) dt + / π
sin(nt) dt + / π 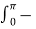 sin(nt) dt
sin(nt) dt
= cos(nt)/nπ | -π 0 - cos(nt)/nπ| π 0 = 1 – cos(-nπ)/nπ - cos(nπ)-1/nπ
= 2/nπ (1-cos(nπ) ) = 2/nπ( 1 – (-1) n) = { 4/nπ for n odd
0 for n even
This then gives the Fourier series for f(t)
f(t) = 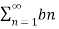 sin(nt) = 4/π ( sint + 1/3 sin(3t) + 1/5 sin(5t) +………………………………….
sin(nt) = 4/π ( sint + 1/3 sin(3t) + 1/5 sin(5t) +………………………………….
Key Take-Aways:
- Fourier series representation in trigonometric series
- Fourier series representation in exponential series
Consider a mass-spring system where we have mass m on spring with spring constant k with damping c and force F(t) applied to the mass. Suppose the forcing function F(t) is 2L periodic for some L>0. The equation governs as
Mx”(t) + cx’(t) +kx(t) = F(t)
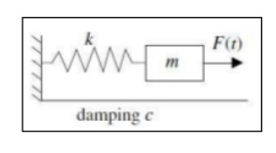
Figure 4. Mass Spring system
The general solution consists of complimentary solution xc which solves the associated homogeneous equation mx”+cx’+kx =0 and the particular solution of (1) we call xp.
For c>0 the complementary solution xc will decay as time goes by. Therefore we are interested in particular solution xp that does not decay and is periodic with the same period as F(t).
Mx” +kx =0 has the general solution
x(t) = A cos(wt) + B sin(wt)
Where
Wo = √k/m
Any solution to mx”(t) +kx(t) = F(t) is of the form A cos(wt) + B sin(wt) +xsp
The steady periodic solution xsp has the same period as F(t)
Hence
F(t) = co/2 + 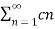 cos(nπ/L) + dn sin(nπ/Lt)
cos(nπ/L) + dn sin(nπ/Lt)
Hence,
x(t) = ao/2 +  cos(nπ/L) + dn sin(nπ/Lt)
cos(nπ/L) + dn sin(nπ/Lt)
Speech or music recognition
Any wave can be written as the sum of sines and cosines. So for example if voice is recorded for one second the Fourier series is given by
Voice= sin(x) + 1/10 sin(2x) + 1/100 sin(3x) +………
This module shows when you add sines /cosines the graph of cosines and sines becomes closer and closer to the original graph. Hence Fourier series is a wave that can be approximated and the second the Fourier series converge fast. Hence it is used in compression. The MP3 format uses audio compression.
Key Take-Aways:
- Application of Fourier series for Mechanical system
- Its application in speech or music recognition
Linearity

Time Shifting

Fs[x(t-to)] = 1/T 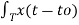 e -jnΩot dt
e -jnΩot dt
Let t-to =p then
Fs(t-to) = 1/T 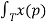 e -jnΩot e -jnΩop dp
e -jnΩot e -jnΩop dp
e -jnΩoto 1/T 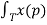 e -jnΩop dp
e -jnΩop dp
e -jnΩoto cn
FS[x(t-to)] = e -jnΩoto cn
Time reversal
If the Fourier series co-efficient of a periodic signal x(t) are cn then the Fourier series co-efficient of the time-reversal of the signal x(t) is given by
FS[x(-t)] = c-n
x(-t) = 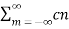 e -jnΩot
e -jnΩot
Let n=-m then
x(-t) =  e -jnΩot
e -jnΩot
Therefore FS[x(-t)] = c-n
Time Scaling
The time-scaled signal of x(t) is denoted as x(at).
If a< 1 the resulting time-scaled signal is an expanded version of x(t).
If a>1 the signal is a compressed version of x(at)
If the fundamental period of x(t) is T then the fundamental period x(at) is T/a.
Multiplication
If x1(t) and x2(t) are both periodic with period T and the Fourier series coefficient of x1(t) and x2(t) are cn and dn respectively then
FS[x1(t) x2(t)] = 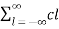 dn-l
dn-l
Proof:
FS[x1(t) x2(t)] = 1/T 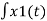 x2(t) e -jlΩot
x2(t) e -jlΩot
x2(t) = 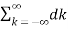 c jkΩot
c jkΩot
= 1/T 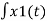
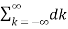 c ejkΩot e -jlΩot
c ejkΩot e -jlΩot
= 1/T 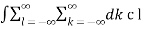 ej(k+l)Ωol e -jlΩot dt
ej(k+l)Ωol e -jlΩot dt
= 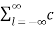 l d n-l
l d n-l
Convolution
If x1(t) and x2(t) are both periodic with T and the Fourier series coeffecients of x1(t) and x2(t) are cn and dn respectively then
FS[x1(t) * x2(t)] = Tcndn
1/T 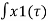 x2(t-τ) dτ
x2(t-τ) dτ
= 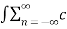 n
n 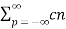 dp
dp  j(n-p)Ωoτ e jpΩot dτ
j(n-p)Ωoτ e jpΩot dτ
= 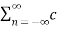 n d n T ejnΩot
n d n T ejnΩot
= FS  (τ) x2(t-τ) dτ = T cn dn
(τ) x2(t-τ) dτ = T cn dn
Parseval theorem
Consider two periodic signals x1(t) and x2(t) with equal period T. If the Fourier series coefficient of these two signals are cn and dn then
1/T 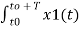 x2(t) = 1/T
x2(t) = 1/T  n e j n Ωot [
n e j n Ωot [  m e jmΩot ] dt---------------------(1)
m e jmΩot ] dt---------------------(1)
= 1/T 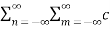 n d *m
n d *m 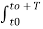 e j(n-m)Ωot dt ------------------------------(2)
e j(n-m)Ωot dt ------------------------------(2)
= 0 n≠ m
=  n d *n n=m --------------------------------(3)
n d *n n=m --------------------------------(3)
If x1(t) = x2(t) = x(t) then eq(3) becomes
1/T 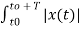 2 =
2 = 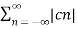 2 --------------------------------(4)
2 --------------------------------(4)
The above equation can be written as
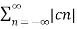 2 = c0 2 +
2 = c0 2 + 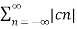 2
2
n≠0
= c0 2 + 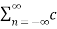 n c *n
n c *n
n≠0
a0 2 + 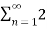 [Re(c 2 n ) + Im (cn ) 2]
[Re(c 2 n ) + Im (cn ) 2]
= a0 2 + 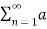 2 n /2 + b 2 n /2 ---------------------------(5)
2 n /2 + b 2 n /2 ---------------------------(5)
Key Take-Aways
- Properties of Fourier series
Gibbs’ phenomenon occurs near a jump discontinuity in the signal. It says that no matter how many terms you include in your Fourier series there will always be an error in the form of an overshoot near the discontinuity. The overshoot always is about 9% of the size of the jump. We illustrate with the example. Of the square wave sq(t).
The Fourier series of sq(t) fits it well at points of continuity. But there is always an overshoot of about .18 (9% of the jump of 2) near the points of discontinuity.
In these figures, for example, ’max n=9’ means we we included the terms for n = 1, 3, 5, 7 and 9 in the Fourier sum
4/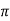 ( sint + sin 3t/3 + sin 5t/5 + sin 7t/7 + sin 9t/9)
( sint + sin 3t/3 + sin 5t/5 + sin 7t/7 + sin 9t/9)
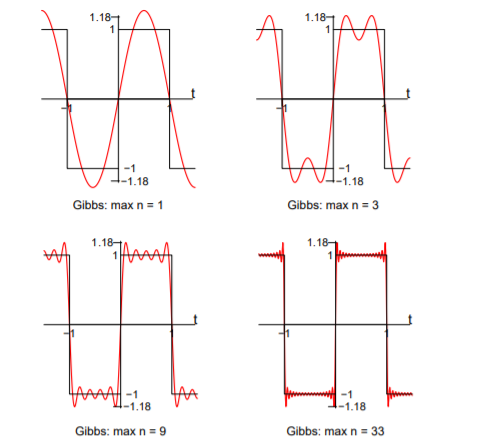
Figure 5. Gibbs Phenomenon
Key Takeaways
- Gibbs Phenomenon its importance
- Application of Gibbs Phenomenon
References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode