Unit 5
Laplace Transform
Consider an LTI system by a complex exponential signal of the form
x(t) = Gest.
Where s = any complex number = σ+jω
σ = real of s, and
ω = imaginary of s
The response of LTI can be obtained by the convolution of input with its impulse response i.e.
y(t)=x(t)×h(t)= 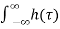 Ges(t-τ) d
Ges(t-τ) d 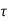
= Gest 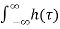 e-sτ d
e-sτ d 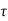
= Gest H(s) = x(t) H(s)
Where H(s) = Laplace transform of h(τ) = 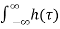 e-sτ d
e-sτ d 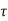
Similarly Laplace transform of x(t) = X(S) =  e-st dt
e-st dt
Example:
Find the Laplace transform of e –t .
F(s) = 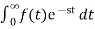
F(s) = 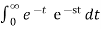
F(s) = 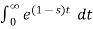
F(s) = 1 / 1-s [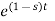 ]0
]0 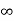
F(s = 1/ s-1.
Find the Laplace transform of unit -step function.
f(t) = 1 (t≥0)
F(s) = 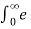 -st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
-st dt = -1/s e -st | 0 ∞ = 1/s [ e -∞ - e -0] = 1
F(s) = 1/s.
Key Take-Aways:
- Definition of Laplace transform
- Laplace transform for various signals like unit step function and exponential
The Fourier transform has led to a very specific and limited view of frequency in the context of signal processing. Simply put, frequencies, in the context of Fourier methods, are just a collection of the individual frequencies of periodic signals that a given signal is composed of.
The Fourier transform is essentially an integral over time. Thus, we lose all information that varies with time. All we can tell from Fourier analysis is that a signal has a number of distinct frequency components. In other words, we can comment on what happens a signal, not when it happens.
Need of Laplace Transform
It’s a very simple integral equation that takes us from the time domain to the frequency domain.
F(s) = 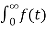 e -st dt
e -st dt
F(s) is the value of the function in the frequency domain and f(t) is the value of the function in the time domain.
Using Inverse Laplace transform you can move back to the time domain from the frequency domain, So, using Laplace and Inverse Laplace transforms you can move back and forth between time domain and frequency domain.
One of the major usages of Laplace transforms is to convert complex differential equations to simple linear equations and help us solve them directly.
This amazing method that solves ODE’s easily helps us understand solution different dynamic systems also helps us explain the frequency response of different dynamic systems and also making the time response analysis easier by simplifying the method to solve differential equations.
Key Take-Aways:
- Limitations of Fourier transform
- Need for Laplace transform
- ROC contains strip lines parallel to jω axis in s-plane.
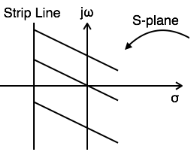
Figure 1. ROC representation
- If x(t) is absolutely integral and it is of finite duration, then ROC is entire s-plane.
- If x(t) is a right sided sequence then ROC : Re{s} > σo.
- If x(t) is a left sided sequence then ROC : Re{s} < σo.
- If x(t) is a two- sided sequence then ROC is the combination of two regions.
Find the Laplace transform and ROC of x(t)=e−atu(t)
- L.T[x(t)]=L.T[e−atu(t)]=1/s+a
Re>−a
ROC:Res>>−a
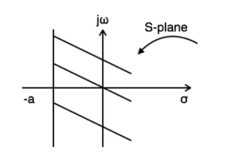
Example 2: Find the Laplace transform and ROC of x(t)=eat u(−t)
- L.T[x(t)]=L.T[eatu(t)]=1/ s−a
- Res<a
- ROC:Res<a
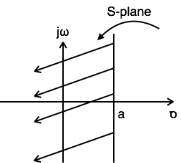
Example 3: Find the Laplace transform and ROC of
x(t)=e−atu(t)+eatu(−t)
L.T[x(t)]=L.T[e−atu(t)+eatu(−t)]
=1/s+a+1/s−a.
- For 1/ s+a Re{s}>−a
- For 1/s−a Re{s}<a
Referring to the above diagram, combination region lies from –a to a. Hence,
- ROC:−a<Res<a
Key Take-Aways:
- What is Region of convergence ?
- Representation of ROC
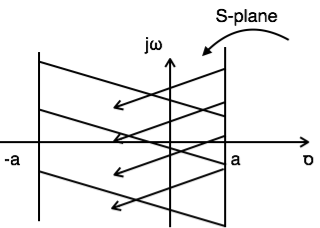
Laplace Transform of Periodic Function.
If a function f(t) is periodic with period p > 0
So that f(t + p) = f(t)
f1(t) represents one period that is one cycle of the function.
Then
L{ f(t)} = L{f1(t)} x 1/ 1- e-sp
Proof:
We know that F(s) = 
=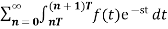
= 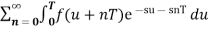 [ u =t – nT]
[ u =t – nT]
=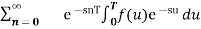
= 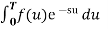 / 1- e-st Because
/ 1- e-st Because  is a geometric series common ratio
is a geometric series common ratio
e −sT < 1 for s > 0.
Example :
Consider f(t) = sin(wt) which is a periodic function of period 2π/ w
F(s) = 1/ 1 – e -2 πs/w 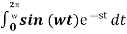
w/ s2 + w2 . 1- e -2 πs/w / 1 – e -2 πs/w = w / s2 + w2
Example:
Find the Laplace transforms of the periodic functions shown below
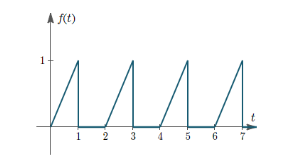
Figure 2. Periodic function
Solution:
From the graph we see that it forms a cycle at t=2.
Hence,
L{ f(t)} = L{ t. u(t)} – L{ t. u(t-1)}
Now L{ t. u(t-1)} = L {(t- 1) . u(t-1)+ u(t-1)}
L{f(t) } = L{t.u(t) }- L{(t-1). u(t-1)} – L{u(t-1)}
= 1/s2 – e-s/s2 – e-s/s
= 1 – e – s – s e –s /s2
= { 1 – e –s – s e –s /s2 } x {1/ 1 –e -2s}
= 1 – e-s – s e –s / s2 ( 1 – e -2s )
F(s) = 1 – e-s – s e –s / s2 ( 1 – e -2s)
Laplace transforms of aperiodic function
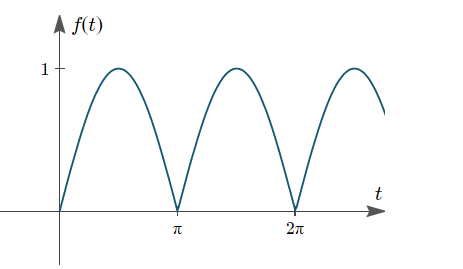
Figure 3. Aperiodic function
f(t)=sin t⋅{u(t)−u(t−π)}, with period π.
Here,
f1(t) = sin t .{ u(t) – u(t-π) }
And period p=π
L{f1(t) }
= L {sin t u(t) } + L {sin(t-π). u(t-π)}
= L { sin t . u(t) + L { sin(t-π) . u(t-π)}
= 1/ s2 +1 + e -πs/ s 2 +1
= 1 + e -πs / s 2 + 1
So, the Laplace transform of the periodic function is given by
L{f(t)} = 1 + e -πs / ( s 2 + 1 ) ( 1 – e – πs)
Key Take-Aways:
- Laplace transform of Periodic function
- Laplace transform of aperiodic function
Linearity:
If x(t) X(s)
And y(t)  Y(s)
Y(s)
Then a x(t) + b y(t)  a X(s) + b Y(s)
a X(s) + b Y(s)
Time Shifting Property
If x(t)  X(s)
X(s)
Then
x(t-to) 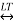 e -sto X(s)
e -sto X(s)
Frequency Shifting Property
If x(t) 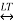 X(s)
X(s)
Then frequency shifting property states that
e so t x(t) 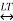 X(s-so)
X(s-so)
Time Reversal Property
If x(t)  X(s)
X(s)
Then time reversal property states that
x(−t)⟷X(−s)
Time Scaling Property
If x(t) 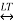 X(s)
X(s)
Then the time scaling property states that
X(at) )⟷X(s/a)
Differentiation and Integration Properties
If x(t) 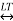 X(s)
X(s)
Then the differentiation property states that
Dx(t) /dt 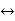 s. X(s) – s. X(0)
s. X(s) – s. X(0)
d n x(t) / dt n 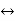 (s) n . X(s)
(s) n . X(s)
The integration property states that
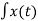 dt
dt  1/s X(s)
1/s X(s)
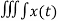 dt
dt  1/s n X(s)
1/s n X(s)
Multiplication and Convolution Properties
If x(t)⟷L.T X(s)
And y(t)⟷L.T Y(s)
Then multiplication property states that
x( t) . y(t)  1/ 2 π j X(s) * Y(s)
1/ 2 π j X(s) * Y(s)
The convolution property states that
x(t) * y(t) 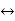 X(s). Y(s)
X(s). Y(s)
Key Take-Aways:
- Properties of Laplace transform
- Significance of these properties
Find the Laplace transform of L (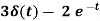 ) .
) .
F(s) = 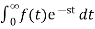
= 3 L((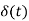 -
- 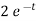 ))
))
= 3 – 2/s-1 [ e-t = 1/s-1]
= 3s-5/s-1.
Find the L(cos t) = s/ s2 + 1
Therefore L( e-t cos t) = s+1/ (s+1)2 + 1
Find the derivative of et
L(f) = 1/s-1
L’(f) = s(1/s-1) – 1
= s/s-1 – 1
= 1/s-1
Find the derivative of sinwt.
L(sin wt) =- 1/w d/dt coswt
L(sin wt) = -1/w ( s s/s2 + w2 - 1 )
= w / s2 + w2
Key Take-Aways
- Evaluation of Laplace transform properties
Consider the transfer function given by
H(s) = 1/ s ( s 2 + 2s + 1)
This equation can also be written as
H(s) = 1/s (s-s2) (s-s3)
And the three system poles are s1,s2 and s3.
s1=0, s2 = -1+j , s3 = -1 -j

Figure 4. Representation of poles
In order to take the inverse Laplace transform we will perform a partial fraction expansion.
H(s) = k1/s + k2 / s-s2 + k3 / s-s3
= k1/s + k2 / s+1-j +k3 / s+1 +j
Each of the constants, which we also call residues, is determined by multiplying H(s) by the pole associated with that constant and evaluating the result at the pole location.
k1 = s H(s) | s=0 = 1/s2 + 2s + 2 | s=0 = 1/ (s-s2)(s-s3)|s=0 = ½
Alternatively, we can use the graphical approach from last time, as depicted in the following diagram
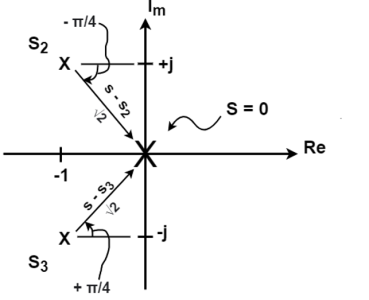
Figure 5. Graphical approach
So, the denominator terms are
(s-s2)| s=0 = 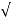 2 e -jπ/4 = √2 x – π/4)
2 e -jπ/4 = √2 x – π/4)
(s-s3) |s=0 = 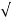 2 e jπ/4 = √2 x + π/4)
2 e jπ/4 = √2 x + π/4)
And K1 is evaluated as
k1 = 1/ (s-s2) (s-s3) | s=0 = 1/ (√ 2 x -π/4)(√2 x π/4) = ½
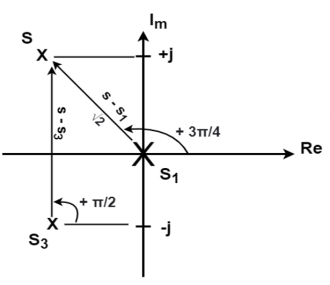
Figure 6. Representation for the above system
Where now
K2 = 1/ (√2 x ¾ π ) ( 2 x π/2) = ( 1/ 2√2 x -5/4 π) = (1/2√2 + 3/4π)
Finally, since K3 must be the complex conjugate of K2
K3 = K2 * (1/2√2 x -3/4 π)
H(s) = 1/2s + ½ √2 ( e ¾ πj / s+1 -j) + 1/2√2 (e -¾ πj / s+1+j)
Thus, we have a sum of first order terms in s, so we can readily obtain the inverse Laplace transform.
h(t) = ½ + 1/2√2 e (-1+j) t e ¾ π j + ½ √2 e (-1-j) t e -3/4 πj
h(t) = ½ + 1/ √2 e -t ( e j(t+3/4 π) + e -j(t + ¾ π) / 2
= ½ + e -t / √2 cos ( t + ¾ π)
Key Take-Aways:
- Inverse Laplace transform
- Methods of Inverse Laplace transform
The stability of an LTI differential system is equivalent to having all the zeros of its characteristic polynomial having a negative real part.
For the Laplace transform, the first stability condition translates into the following:
An LTI system is stable if and only if the ROC of its transfer function contains the axis.
Consider an LTI system with proper transfer function:
H(s) = s(s+1)/(s+2)(s-1)
Three possible ROCs could be associted with this transfer function gives the impulse response for each ROC. Only one ROC leads to a stable system. Note that the system poles are marked with an X and the system zeros are marked with an O in the s-plane.
First let us compute the partial fraction expansion of H(s)
H(s) = s(s+1)/ (s+2)(s-1) = A + B/s-1 + C / s+2
A=1, B = 2/3 , C =-2/3
Hence the transfer function can be expanded as
H(s) = s(s+1) / (s+2)(s-1) = 1 + 2/3 . 1/ s-1 – 2/3 . 1/s+2
The first term is constant and corresponds to an impulse. The two other terms are partial fractions that can correspond to right-sided or left-sided signals, depending on the chosen ROCs. The stability condition for a causal LTI system with a proper, rational transfer function is stated as follows. Note that a large class of causal differential LTI systems has rational transfer functions.
Key Take-Aways:
- Stability of the system
- Condition for stability
We have seen that the transfer function of an LTI system is the Laplace transform of its impulse response. For a differential LTI system the transfer function can be readily written by inspecting the differential equation just like its frequency response can be obtained by inspection.
Consider the general form of LTI differential system:
 k d k y(t) / dt k =
k d k y(t) / dt k =  K d k x(t) / d tk ------------------------------(1)
K d k x(t) / d tk ------------------------------(1)
We use the differentiation and linearity properties of Laplace transform to obtain the transfer function H(s) = Y(s) / X(s) = 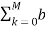 K s k /
K s k / 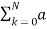 k s k -----------(2)
k s k -----------(2)
Note that we have not specified a region of convergence (ROC) yet. This means that differential equation (1) can have many different impulses that is it is a complete specification of LTI system. If we know that the differential system is casual then ROC is open right half plane to the right of the rightmost pole in s-plane . The impulse response is then uniquely defined.
Key Take Aways:
- Application of Laplace transform in LTI system
- ROC
References:
Signals and Systems by Simon Haykin
Signals and Systems by Ganesh Rao
Signals and Systems by P. Ramesh Babu
Signals and Systems by Chitode