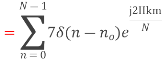UNIT 4

DFT

4.1 Discrete Time Fourier Transform

The discrete-time Fourier transform (DTFT) or the Fourier transform of a discrete–time sequence x[n] is a representation of the sequence in terms of the complex exponential sequence ejωn.

The DTFT sequence x[n] is given by

X (w) = 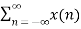  e-jwn --------------- (1)

Here X (w) is a complex function of real frequency variable w and can be written as

X (w) = Xre (w) + j X img (w)

Where Xre (w), j X img (w) are real and Imaginary parts of X(w)

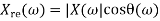
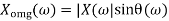
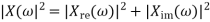
And | X (w)|   can be represented as

.

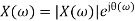Inverse Discrete Fourier Transform is given by

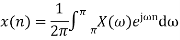
Problems:

Find the four point DFT of the sequence

X (n) = {0, 1, 2, 3}

Here N=4. W40 = e-j2πn/4 = e-j π/ 2 = cos 0 – j sin = 1   for n=0

W41 = e-j2 π/4 = cos π/2 – j sin π /2 = -j

W42 = e-j π = cos π – j sin π = -1

W43    = e-j2.3 π/4 = cos 3 π/2 – j sin 3 π/2 = j

For k=0

X (k) = 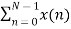e-j2 π nk/N

X (0) =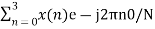 

X (0) = x (0) + x (1) +x (2) + x (3) = 0 +1+2+3 = 6

X (1) = 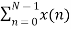e-j2 π nk/N

X (1) = 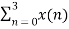e-j2 π n/4

= x (0) e0 + x (1) e –j2 π /4+ + x (2) e-j4 π/4+ x (3) e- j 6 π/4

= 0 + 1 –j + 2(-1) + 3(j)

= -2+ 2j

X (2) = 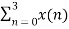e-j2 π n2/4

X (2) = 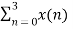  e-j π n

X (2) = x (0) 1+ x (1) e-j π + x (2) e-j2 π + x (3) e-j3 π 

X (2) = -2

X (3) = 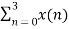e-j2 π n3/4

X (3) = x (0) e0 + x (1) e-j3 π/2   + x (2) e-j3 π + x (3) e-j9 π/2

X (3) = -2-2j.

DFT = {6, -2+2j,-2, 2-2j}

4.2 Properties of DTFT

Linear Property

If x(t) -> X(w)

Y(t) -> Y(w)  then

a x(t) + b y(t)  -> a X(w) +b Y(w)

Time Shifting Property

If  x(t)⟷F.TX(ω)

Then Time shifting property states that

x(t−t0)⟷F.T   e−jω0t X(ω)

Frequency Shifting Property

If x(t)⟷X(ω)

Then frequency shifting property states that

Ejω0t.x(t)⟷X(ω−ω0)

Time Reversal Property

If x(t)⟷X(ω)

Then Time reversal property states that

x(−t)⟷X(−ω)

Differentiation Property

If x(t)⟷X(ω)

Then Differentiation property states that

Dx(t)dt⟷jω.X(ω)

dnx(t)dtn⟷(jω)n.X(ω)

Integration Property

Integration property states that

∫x(t)dt⟷1jω X(ω)

Then

∭...∫x(t)dt⟷(jω)n X(ω)

Multiplication and Convolution Properties

If x(t)⟷X(ω)

y(t)⟷Y(ω)

Then multiplication property states that

x(t).y(t)⟷X(ω)∗Y(ω)

And convolution property states that

x(t)∗y(t)⟷1/2πX(ω).Y(ω)

Numericals:

1. Compute the N-point DFT of x(n)=3δ(n).

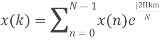
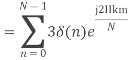
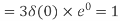
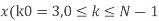
2.     Compute the N-point DFT of x(n)=7(n−n0)

Solution − We know that,

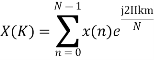
Substituting the value of x(n),