Unit 2
Time-Domain Analysis
Time Response Analysis:-
For a second order control system, the total time response is analyzed by its transient as well as ready state response.
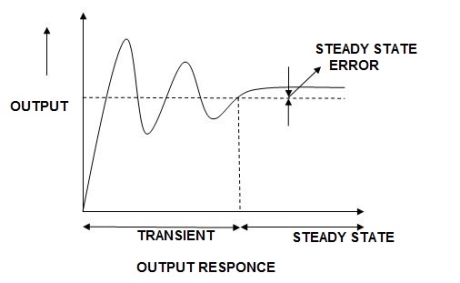 Any system which contains energy along elements (L1 c etc) if suffer any disturbance in the energy state effect at the input end as at this output or at both the ends takes source time to change in thus form one state other . This change its then is called as Transient times and the values of reverent and voltage during this period is Transient Response.
Any system which contains energy along elements (L1 c etc) if suffer any disturbance in the energy state effect at the input end as at this output or at both the ends takes source time to change in thus form one state other . This change its then is called as Transient times and the values of reverent and voltage during this period is Transient Response.
The above fig: a clearly shows steady star response is that part of response when the transient have died. If the steady star response of the output does not match with input then the system has steady state errors.
Consider the following open loop system
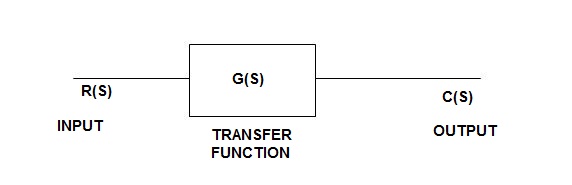
L-1[c(s)]= L-1[ G(s) R (S)]
C(t) = L-1[ G(S) Q (s)]
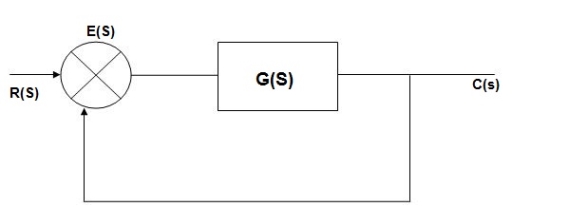
E(s) = R(s) –c(s) [ error signal]
C(S)= [ R(s)- c(Q)] G(s)
C(s) = R(s) G(s)- c(s) G(s)
C(s) [ 1+G(s)] = R(s) G(s)
C(s)/R(s) = G(s)/1+G(s)
C(s)/R(s) = G(s)/1+G(s)
E(s) = R(s)- c(s)
=R(s)-R(s) G(s)/1+G(s0
E(s) = R(s) [1/1+G(s)
If no error then E(s) = 0, f(t) = 0 Hence , r(t) = c(t)
Now calculating errors of when order is varied
1) Order 1 :
OLIF G(s) = 1/TS
CLIF c(s)/R(s) = 1/1+TS
CE : HTS = 0
S= -1/T
C(s) = R(s) [G(S)/1+G(s)]
C(s) = R(s)/1+TS
So, Calculating value of c(s) , c(t) for different input
a) Unit slip:-
R(t) = u(t)
R(s) = 1/s
C(s) = 1/s(1+ST)
1/s(1+ST) = A/s + o/1+TS
1/s(1+ST) = A/S + 0/1+TS
1= A(1+ST) + BS
AT +B =0
A = 1
B= -T
C(s) = 1/s + (-T)/1+TS
= 1+ (-T)/1-(-T)s = 1-I/n/1+ass+1/T =e-t/s
 C(t) = [ 1-e-t/T]
C(t) = [ 1-e-t/T]
Ramp:-
R(t) = t
R(s) = 1/s2
C(s) = R(s) [G(s)/1+G(s)]
C(s) = 1/s2 1/(1+TS) + c
1/s2 (1+TS) = A/(s) + B/s2 + c(1+TS)
1 = A(s+s2. T) + B(1+TS) +cs2
TA +c = 0
A+TB =0
B =1
A = -T
C = T2
C(s) = -T/s + 1/s2 +T2/1+ST
=(-T) u(t) + t(u) + T e-t/T u(t)
= [ -T + t +Te-t/T u(t)
= [ -T+ t+Te-t/T] u(t)
C(s) = t- T+ Te-t/T
ess = 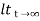 R(t) – c(t)
R(t) – c(t)
= 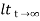 [ t- t+ 7-Te –t/T]
[ t- t+ 7-Te –t/T]
= 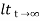 T( 1-e-t/T]
T( 1-e-t/T]
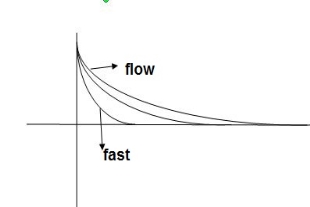
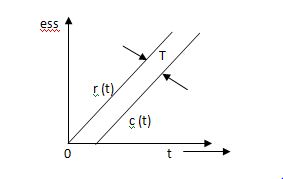 ess = T The less the value of T the less in the errors.
ess = T The less the value of T the less in the errors.
Inference:-
From both the Cases input unit step, ramp Unit slip
r(t) = 1 Ramp
c(t) = 1-e-t/T r(t) = t
ess = e-t/T (r/t)-(t) c(t) = t- T+te-t/T
ess= e-t/T (r/t) (t) ess = T- Te-t/T
For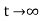 :- for
:- for :-
:-
ess =0 ess = T
In both the vases (values of T) must be as small as possible ( so, that e-t/T) must be as small as possible which gives us
G(s) = 1/Ts
ATf = 1/1+TS
1st order system
Poles must be situated as for as possible from origin i.e. deeper and deeper into the left half of s-place . Thus we get less errors.
Time response analysis of second order system
2) ORDER – 2
OLTF G(s) = k/s(1+TS)
CLTFC(s)/R(s) = k/k+s(1+Ts)
= k/s2+ s/T +k/T
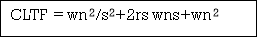 Comparing above equation with standard 2nd order eqn
Comparing above equation with standard 2nd order eqn
Standard 2nd order equation
CEs2+2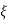 wn s+wn2= 0
wn s+wn2= 0
S= -2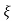 wn±
wn±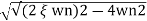 /2
/2
=2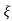 wn±2wn
wn±2wn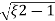 /2
/2
S=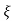 wn±wn
wn±wn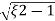
S= -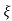 wn±wn
wn±wn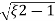
S= -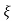 wn ±wn
wn ±wn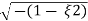
S= -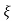 wn ±gwn
wn ±gwn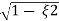
Standard eqn:-
T(s) = wn2/s2+2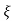 wns+wn2
wns+wn2
Our eqn T(s) = K/T/s2+1/T s+ K/T
Wn2 = k/T
2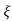 wn = 1/T
wn = 1/T
2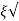 k/T = 1/T
k/T = 1/T
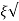 k/T = 1/2T
k/T = 1/2T
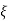 = 1/2T
= 1/2T 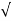 T/K
T/K
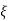 = 1
= 1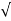 2KT
2KT
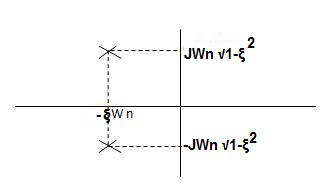
Graphically showing the position of loops s1,s2 for offered of
As the chara Equn (location of polls ) is depend ent only on r (wn constant for a given system)
S1 = -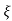 wn + jwn
wn + jwn 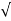 1-
1-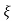 2
2
S2= -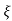 wn - jwn
wn - jwn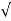 1-
1-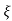 2
2
CASE 1: (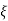 =0)
=0)
S1=jwn,S2, = -jwn
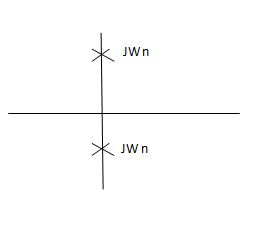
Undamped
CASE 2:(0<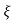 <1)
<1)
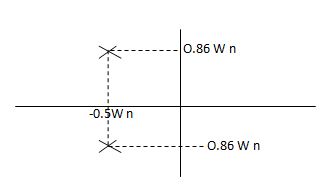
S1= -wn + jwn 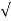 0.75
0.75
=-wn/2 +jwn(0.26)
S2 = -wn/2 – jwn (0.86)
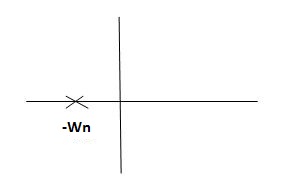
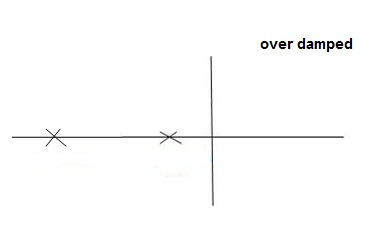
CASE:3 (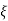 -1)
-1)
S1= S2 = -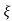 wn = -wn
wn = -wn
CASE4:- (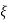 -1)
-1)
S1 = -2wn +jwn  -3
-3
=-2wn – jwn (1.73)
S1 = -3.73wn
S2 = -2wn –jwn  -3
-3
= -2wn + jwn (1.73)
= -0.27  wn
wn
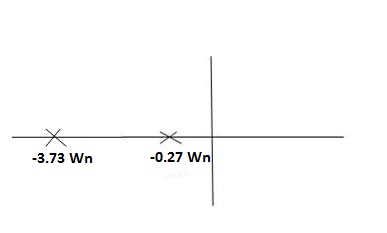
Overdamped
All practical sys are 2 order to, if R(e) = 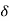 (t) R(s) = 1 :. CLTF = 2nd order system eqn and hence already the system is possible.
(t) R(s) = 1 :. CLTF = 2nd order system eqn and hence already the system is possible.
CLTF = e(s)/ R(s) = wn2/s2+2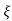 wns+wn2
wns+wn2
Now calculating c(s) , c(t) for different values of input
1) Impulse I/p
R(t) = 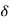 (t)
(t)
R(s) = 1
C(s) = R(s) wn2/s2+2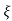 wns+wn2
wns+wn2
C(s) = wn2/s2 +2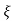 wn+wn2
wn+wn2
Under this i/p (R(t) = 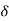 (t)) the output varies with different values of
(t)) the output varies with different values of 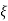 . So,
. So,
CONDITION 1: (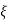 =0)
=0)
C(s) =wn2/s2 +wn2
Os2 +wn2 =0
S=+-jwn
C(t) = wn sinwnt
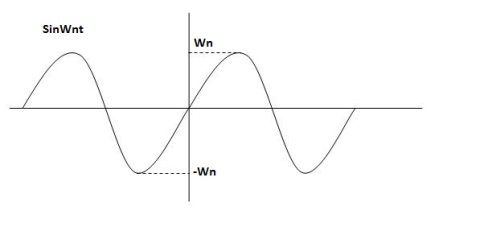 Sinwnt
Sinwnt
As there in no damping i.e. oscillations at t= 0 are some at t  so, called UNDAMPED
so, called UNDAMPED
CONDITION 2: 0<<1
c(s) = R(s) wn2/s22 wn+wn2 R(t) =
wn+wn2 R(t) = 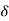 (t)
(t)
R(s) =1
C(s) = wn2/s2+2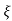 wns+wn2
wns+wn2
CE
S2+2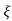 wns +wn2 =0
wns +wn2 =0
S2, S1 = -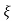 wn ±jwn
wn ±jwn 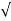 1-
1-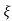 2
2
C(t) = e-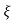 wnt sin( wn
wnt sin( wn 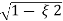 )t
)t
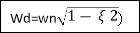
C(t)=e- wnt sin (wdt)
wnt sin (wdt)
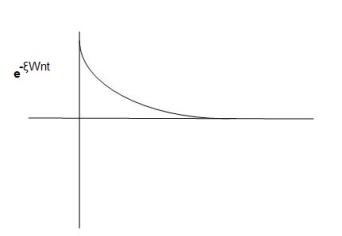
The oscillations are present but at t- infinity the Oscillations are 0 so, it is UNDERDENPLZ
CONDITION 3 : =1
=1
C(s) = R(s) wn2/s2+2 wns+wn2
wns+wn2
C(s)=wn2/S2 +2wns+wn2
=wn2/(s +wn)2
CE S= -Wn
Diagram
C(t)= w2n /(
w2n /(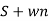 )2
)2
C(t)=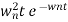
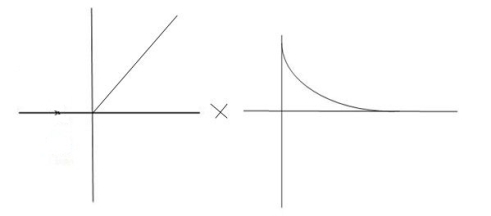
No damping obtained at 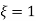 so is called CRITICALLY DAMPED.
so is called CRITICALLY DAMPED.
CONDITIONS 4 :- >1
>1
C(s) = wn2/s22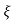 wnS+Wn2
wnS+Wn2
S1,s2 = 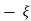 WN+-jwn
WN+-jwn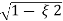
b)UNITStep Input:-
R(s) = 1/s
C(s)/R(s) = wn2/s2+2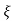 wns+wn2
wns+wn2
C(s) = R(s) wn2 /s2 +2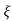 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2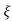 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2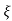 wns+wn2
wns+wn2
C(s) = wn2s(s2+2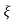 wns+wn2)
wns+wn2)
C(t) = 1- e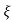 wnt/
wnt/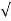 1-es2 sin (wdt + ø)
1-es2 sin (wdt + ø)
Wd = wn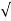 1-
1-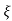 2
2
Ø= 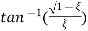
Where
Wd = Damping frequency of oscillations
Wn = natural frequency of oscillations
 wn = damping coefficient.
wn = damping coefficient.
T= Time constant
Condition 1 = 0
= 0
C(s) = wn2 /s(s2+wn2)
C(t) = 1- e° sin wdt +ø
C(t)= 1- sin( wn +90)
C(t) = 1+cos wnt
Constant
C(t) = 1+constant
Condition 2:- 0<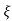 <1
<1
C(s) = 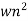 /s2+
/s2+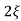 wns +wn2
wns +wn2
C(s) =1/s – s+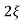 wn/s2+
wn/s2+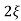 wns +wn2
wns +wn2
=1/s – s+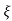 wn/(s+
wn/(s+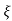 wn)2+wd2-
wn)2+wd2- 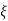 wn/(s+
wn/(s+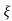 wn2) +wd2
wn2) +wd2
Wd = wn 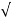 1-
1-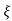 2
2
Taking Laplace inverse of above equation
L --1 s+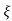 wn/(s+
wn/(s+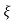 wn) +wd2= e-
wn) +wd2= e-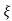 wnt cos wdt
wnt cos wdt
L-1 s+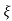 wn/(s+
wn/(s+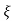 wn)2+wd2 = e-
wn)2+wd2 = e-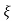 wnt sinWdt
wnt sinWdt
C(t) = 1-e-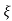 wnt [coswdt +
wnt [coswdt +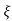 /
/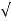 1-
1-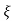 2 sinwdt]
2 sinwdt]
= 1-e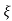 wnt /
wnt /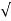 1-
1-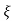 2 sin [wdt +
2 sin [wdt + 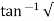 1-
1-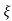 2/
2/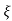 ] t>=0
] t>=0
C(t) = 1-e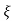 wnt/
wnt/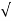 1-
1-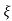 2 sin(wdt+ø)
2 sin(wdt+ø)
Ø = 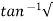 1+
1+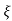 2/
2/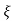
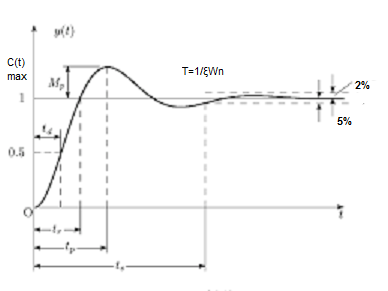
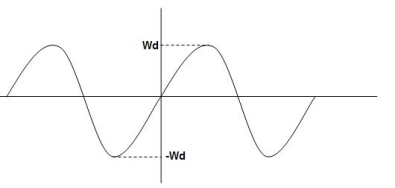
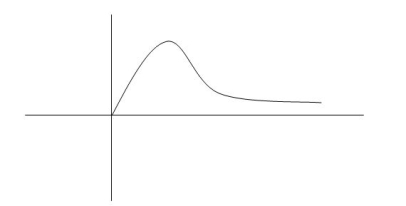
Fig 6. Transient Response of second order system
Specifications:
1) Rise Time (tp):- The time taken by the output to reach the already status value for the first time is known as Rise time.
C(t) = 1-e-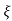 wnt/
wnt/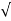 1-
1-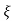 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n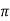
tr =n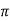 -ø/wd
-ø/wd
For first time so ,n=1.
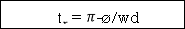
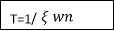
2) Peak Time (tp)
The peak value attained by the output is called peak time .The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n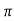 /wd for n=1
/wd for n=1
tp = 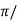 wd
wd
(3) Peak Overshoot Value :-
Maximum deviation of output from steady state value is called peak overshoot value(Mp ).
( ltp ) = 1 = Mp
(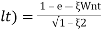 Sin(Wat + φ )
Sin(Wat + φ )
(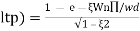 Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
(4). Settling Time (ts) :
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Q.1. The open loop transfer function of a system with unity feedback gain G( S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Soln : Finding closed loop transfer function,
C( S ) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Setteling time (v) Peak overshoot.
Soln: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by
G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Soln: C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
Forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Soln:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
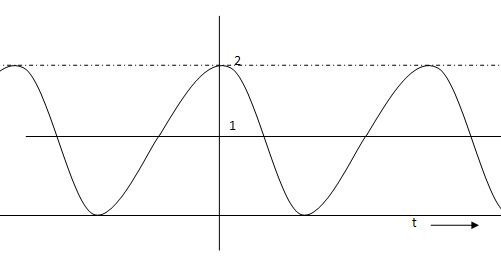
The Impulse signal, Ramp signal, unit step and parabolic signals are used as the standard test signals. All these signals are explained below.
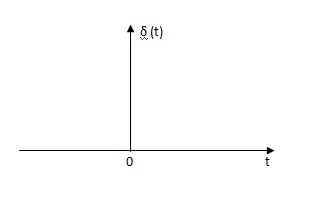
Impulse Signal:-
This signal have zero amplitude every where expect at the origin. Fig below shown the representation of Impulse signal.
The mathematical representations
A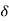 (t) = 0 for t ≠0
(t) = 0 for t ≠0
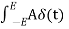 dt = A e
dt = A e 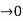
Where A represent energy or area of the Laplace Transform of Impulse signal is
L [A (t) ]= A
(t) ]= A
UNIT IMPULSE SIGNAL :-
If A = 1
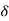 (t) = 0 for t ≠0
(t) = 0 for t ≠0
L [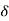 (t)] = 1
(t)] = 1
The transfer function of a linear time invariant
System is the Laplace transform of the impulse response of the system. If a unit impulse signal is applied to system then Laplace transform of the output c(s) is the transfer function G(s)
As we know G(s) = c(s)/R(S)
r(t) = 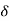 (t)
(t)
R(s) = L [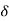 (t)] = 1
(t)] = 1
:. G(S) = C(s)
(b) Step signal:-
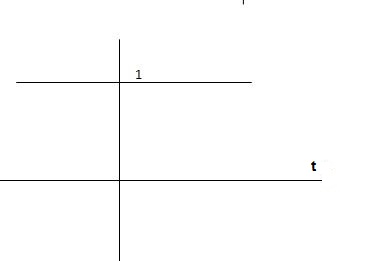
Step signal of size A is a signal that change from zero level to A in zero time and stays there forever.
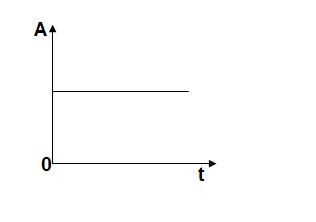
r(t)= A t >=0
=0 t<0
L[r(t)]= R(s) = A/s
UNIT STEP SIGNAL :- If the magnitude of the slip signal is I then it is called unit step signal.
u(t) = 1
t>=0
t<0
L[u(t)] = 1/s
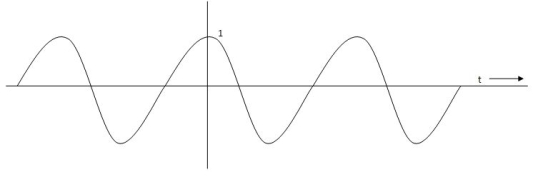
(c) Ramp Signal:-
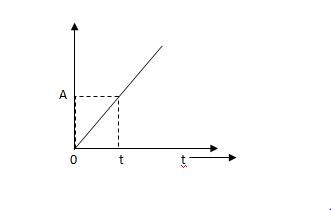 The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
r(t) = At t>=0
=0 t<0
A is the slope of the line The Laplace transform of ramp signal is
L[r(t)] = R(s) = A/s2
(d) Parabolic Signal:-
The instantaneous value of a parabolic signal varies as square of the time from an initial value of zero t=0. The signal representation in fig 14 below.
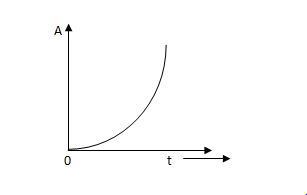
r(t) At2 t>=0
=0 t<0
Then Laplace Transform is given as
R(s) = L[At2] = 2A/s3
If no error then E(t) =0 , :. R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess) :- ( t  )
)
ess = t 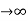 e(t)
e(t)
Using final values the theorem
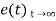 = ess =
= ess = 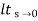 S.E (s)
S.E (s)
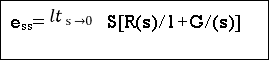
Steady state error and error constant
So, for difficult input, ess will be different Input still be
1) R(s) = unit step (3) R(s) = parabolic
2) R (s) = Ramp
1) R(s)= Unit step
R(t) = u(t)
R(s) = 1/s
ess = 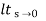 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 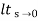 s[ys/1+G(s)]
s[ys/1+G(s)]
ess= 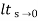 1+1/1+G(s)
1+1/1+G(s)
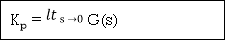 =1/1+lt G(s) s- 0
=1/1+lt G(s) s- 0
(Position error coefficient)
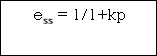
1) R(s) = Ramp
R(t) = t
R(s) = 1/s2
ess=  s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
=  s[ys2/1+G(s)]
s[ys2/1+G(s)]
=  1/s(1+G(S)
1/s(1+G(S)
=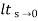 1/s+SG(s)
1/s+SG(s)
ess =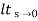 l/s-0 SG (s)
l/s-0 SG (s)
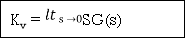 ess =
ess = 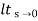 t L/SG (s)
t L/SG (s)
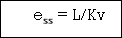 velocity errors coefficient
velocity errors coefficient
(3)Parabolic
R(t) = t2
R(s) =1/s3
Ess = 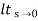 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 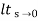 s(1/s3)/1+G(s)
s(1/s3)/1+G(s)
= 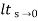 1/s2+s2G(s)
1/s2+s2G(s)
 Ess =
Ess = 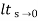 1/s2G(s)
1/s2G(s)
Acceleration error coefficient
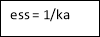
I/p error coefficient
(1)Unit step ess= 1/1+kv kv = 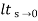 G(S)
G(S)
(2)Ramp ess= 1/kv kv = 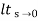 sG(s)
sG(s)
(3)Parabolic ess = 1/ka ka = 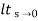 s2 G(s)
s2 G(s)
Now finding errors in type 0,1,2 system
1) Type 0:-
G(s) = 1/(s+a) (s+b)
2) Kp :
Kp =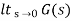
=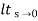 1/(s+a)(s+b)
1/(s+a)(s+b)
Kp= 1/ab
Ess=1/1+np = 1/1+(1/ab) 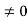
o/p not locking the input
(b) kv:-
Kv = 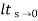 s G(s)
s G(s)
= 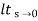 s/(s+a) (s+b)
s/(s+a) (s+b)
=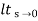 s/(s+a) (s+b)
s/(s+a) (s+b)
Kv = 0
ess = 1/kv = 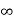
o/p not locating the input
(3)ka:-
Ka = 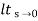 s2 G(s)
s2 G(s)
= 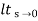 s2 /(s+a) (s+b)
s2 /(s+a) (s+b)
Ka =0
ess = 1/ka = 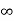
o/p not locking the input
(2)Type –I :-
G(s) = 1/s(s+a) (s+b)
(a)Kp:-
Kp = 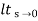 G(s)
G(s)
=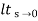 1/s(s2+as+ab)
1/s(s2+as+ab)
Kp = 1/0 = 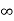
ess = 1/1+kp = 0
o/p is tracking the input
(b)kv:-
Kv = 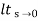 S G(s)
S G(s)
=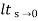 1/(s+a) (s+b)
1/(s+a) (s+b)
=1/ab
Kv = 1/ab
ess =1/ka = ab 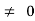
o/p is not tracking the input
3)ka :
Ka= 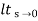 s2G(s)
s2G(s)
= 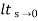 s2 /s(s+a)(s+b)
s2 /s(s+a)(s+b)
= 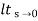 s/(s+a)(s+b)
s/(s+a)(s+b)
Ka= 0
Ess = 1/ka = 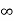
O/p is not tracking the input .
3) Type 2 :-
G(s) = 1+/(s2(s+a) (s+b)
a) Kp:-
Kp = 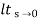 G(s)
G(s)
= 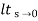 1/s2 (s+a) (s+b)
1/s2 (s+a) (s+b)
Kp = 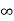
ess = 1/1+kp = 0
o/p tracking the i/p
b) kv:-
Kv =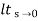 s G(s)
s G(s)
=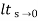 1/s(s+a) (1+b)
1/s(s+a) (1+b)
kv = 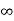
ess =1/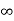 = 0
= 0
o/p tracking the o/p
(b) ka:-
Ka= 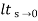 s2G(s)
s2G(s)
=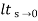 1/(s+a) (s+b)
1/(s+a) (s+b)
Ka = 1/ab
ess = 1/(yab) ≠0
o/p not locking the i/p
|
Unit step ≠0 0 0 |
Ramp  |
Parabolic  |
Effects of controller are viewed on time response and stability.
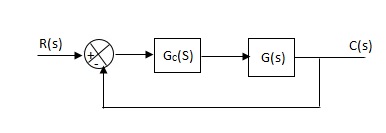
Gc(S) = TF of the controller
G(S) = OLTF without controller
G’(S) = Gc(S).G(S)
= OLTF with controller
(1). Proportional Controller :-
Proportional means scalar Multiplier.
Gc(S) = Kp Stability can be controlled
Q. G(S) = 1/S(S + 8)
CLTF = 1/S2 + 8S + 1
w2n = 1
wn = 1
2ξWn = 8
ξ = 4
ξ>/1 so, overdamped.
Now introducing Gc(S) = K
G’(S) = Kp/S(S + 8)
CLTF = Kp/S2 + 8S + Kp
wn = √Kp
2 ξwn = 8
ξ = 4/√Kp
If,
Kp = 16; ξ = 1; critically damped
Kp> 16; ξ< 1; undamped
Kp< 16; ξ> 1; overdamped
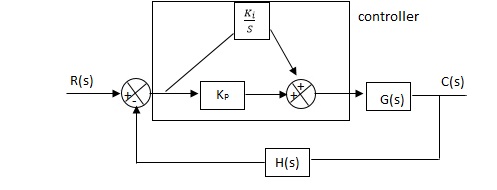
(2). Integral controller:-
The transfer function of this controller is
Gc(S) = Ki/S
Integral controller are used to improve the steady state response or reduce the steady state error.
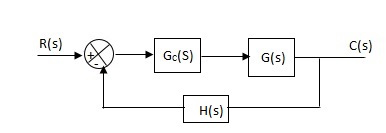
G’(S) = Gc(S).G(S)
G(S) = 1/S + 5, Gc(S) = Ki/S
G’(S) = Ki/S(S + 5). After applying the Gc(S) the type of system is increasing and hence, the steady state error is decreasing (Refer Time Response).
Disadvantage :-
By using integral controller the stability of closed loop system decreases.
G(S) = 1/S + 5
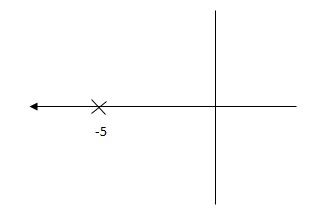
G’(S) = Ki/S(S + 5)
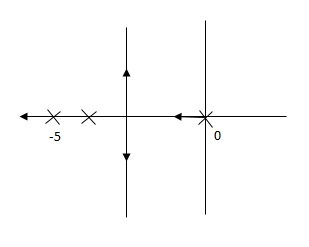
Fig(1), is more stable than (2) as more the away the pole from origin (imaginary axis) more is the stability.
Q. G(S) = 1/(S + 5)(S + 10)
G’(S) = Kp/S(S + 5)(S + 10)
G(S) = 1/(S + 5)(S + 10)
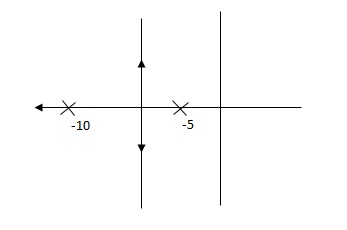
G’(S) = Ki/S(S + 5)(S + 10)
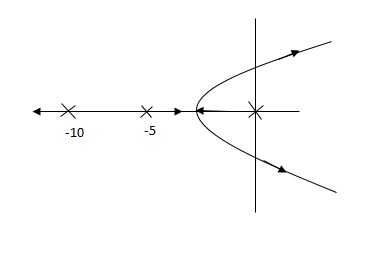
So, (b), is less stable at root locus lies on the R.H.S,
(3). Derivative Controller :-
Gc(S) = Kd(S)
They are used to improve the stability.
G’(S) = KdS/S2(S + 10)
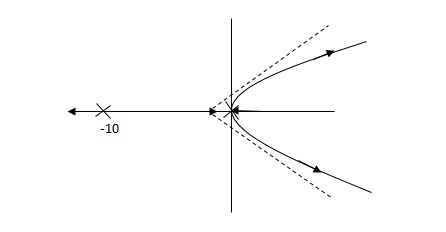
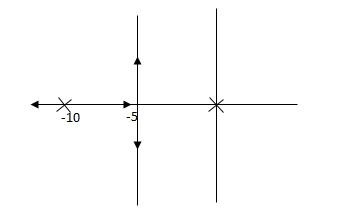
(b) is stable i.e. more stable than the (a).
Disadvantage :-
It increases the steady state i.e. o/p will not track the input at steady state.
(4). Proportional Plus Integral [PI] controller :-
Gc(S) = KpS + Ki/S
The steady state error will decrease and the stability will depend on Kp i.e. if Kp is increased/decreased than according to it stability will change(Kpα stability).
Used to reduce ess without much affecting the stability.
(5). Proportional Plus Derivative Controller :-
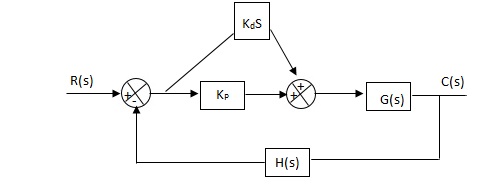
Used to improve the stability without affecting much the steady state error.
(6). PID controller :-
Gc(S) = Kp + Ki/S + KdS
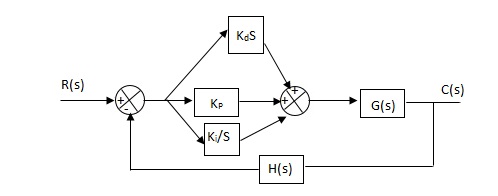
It improves the stability. It decreases the steady state error and both are proportional to Kp.
Q.The block diagram of a system using PI controllers is shown in the figure. Calculate :
(a). The steady state without and with controller for unit step input?
(b). Determine TF of newly constructed sys. With controller so, that a CL Poles is located at -5?
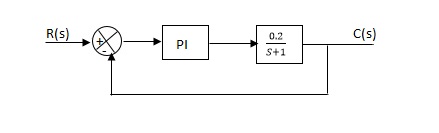
(a). Without :
C(S)/R(S) = 0.2/(S + 1)
C(S) = R(S) 0.2/(S + 1) + 0.2
For unit step
Ess = 1/1 + Kp
Kp = lt G(S)
S 0
= lt 0.2/(S + 1)
S 0
Kp = 0.2
Ess = 1/1.2 = 5/6 = 0.8
(b). With controller :
Gc(S) = Kp + Ki/S
G’(S) = Gc(S).G(S)
= ( Kp + Ki/S )0.2/(S + 1)
= (KpS + Ki)0.2/S(S + 1)
Ess = 1/1 + Kp = 0
So, the value of ess is decreased.
(b). Given
Kpi/Kp = 0.1
G’(S) = (Kp + Ki/S)(0.2/S + 1)
= (KpS + Ki)0.2/S(S + 1)
As a pole is to be added so, we have to examine the CE,
1 + G’(S) = 0
1 + (Kp + Ki)0.2/S(S + 1) = 0
S2 + S + 0.2KpS + 0.2Ki = 0
S2 + (0.2Kp + 1)S + 0.2Ki = 0
Given,
Kpi = 0.1Ki
Kp = 10Ki
S2 + (2Ki + 1)S + 0.2Ki = 0
Pole at S = -5
25 + (2Ki + 1)(-5) + 0.2Ki = 0
-10Ki – 5 + 25 + 0.2Ki = 0
-9.8Ki = -20
Ki = 2.05
Kp = 10Ki
= 20.5
Now,
G’(S) = (KpS + Ki)(0.2)/S(S + 1)
= (20.5S + 2.05)(0.2)/S(S + 1)
G’(S) = 4.1S + 0.41/S(S + 1)
Q.The block diagram of a system using Pd controller is shown, the PD is used to increase ξ to 0.8. Determine the T.F of controller?
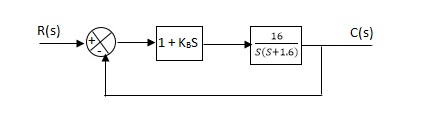
(1). Kp = 1
Without controller:-
C(S)/R(S) = 16/S2 + 1.6S + 16
wn = 4
2 ξwn = 16
ξ = 1.6/2 x 4 = 0.2
(b). With derivative :-
ξS = 0.2 to 0.8
Undamped to critically damped,
G’(S) = (1 + KdS)(16)/(S2 + 1.6S)
CE:
S2 + 1.6S + 16(1 + KdS) = 0
S2 + (1.6 + Kd)S + 16 = 0
2 ξwn = 1.6 + Kd1.6
wn = 4
ξS = 0.8
2 x 4 x 0.8 = 1.6 + Kd1.6
6.4 – 1.6 = Kd1.6
4.8/16 = Kd
Kd = 0.3
TF = (1 + 0.3S)16/S(S + 16)
Ss2.5 Limitations of time domain analysis
The analysis in time domain is very difficult. The stability analysis in time domain is very tiresome. As the order of the system increases the calculation of stability of system becomes very difficult.


