Unit 4
Stability and Compensation Techniques
Concept of Stability:
A stable system always gives bounded output for bounded input and the system is known as BIBO stable
A linear time invariant (LTI) system is stable if,
The system is BIBO stable
In absence of the input the output tends towards zero

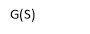 For system;
For system;

 1) R(S)
1) R(S)

For R(s) = 1
C(S) = 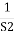
R (t) = 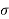 (t) C (t) = t
(t) C (t) = t



 R(t)
R(t)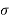 (t)
(t)
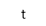
T Bounded Unbounded
So, system unstable.

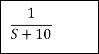

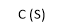 Eg.2 R(s)
Eg.2 R(s)
[R(s) = 1]
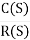 =
= 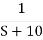
C(t) = e-10tC(t)


 t= 0
t= 0
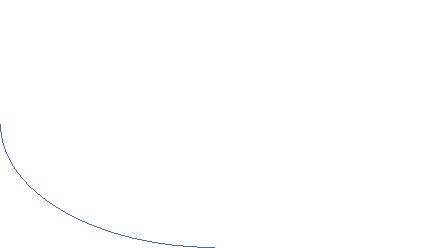 e-10t
e-10t
 t
t
 e-10tC(t) 1
e-10tC(t) 1
0 t
BIBO stable figure
Effect of location of Poles on stability
A) Real and negative G(s)= 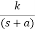
C(t)
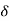
-a


Stable
B) Poles on right half of S- plane
G(s) = 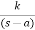
 Iw C(t)
Iw C(t)

 a
a
0 t
Unstable:- Unbounded Output
(C)Poles at origin
G(s)=


 iw C(t)
iw C(t)

k

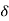 t
t
Marginally stable
Fig 9.(c)
4) Complex poles on left half of S-plane
S1,S2= -α ± iw
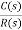 =
= 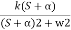
C(t) = k e- αt Cos wt
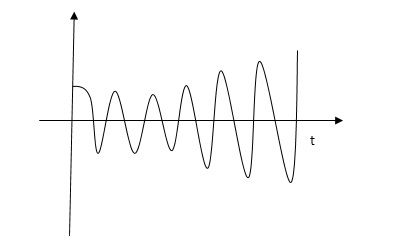
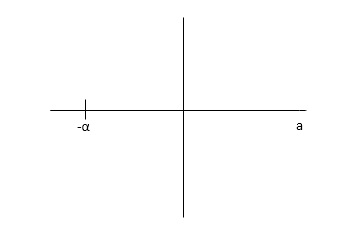
Fig 9(d)
At t - ∞ C(t) – 0 so, system stable
5) Complex poles on right half of S-plane
S1,S2 = α ± iw.
C(t) = k eαt COS wt.
Fig 9 (e)
 C(t) increases exponentially with t ∞
C(t) increases exponentially with t ∞
So, unstable.
6) Poles on iw axis:
S1,S2 = ± iw.
C(t) = k COS wt.


0 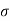
Fig 9 (f)
The system is marginally stable than sustained oscillations.
Consider a system with characteristic equation
aoSm+ a1 Sm-1……………..am=0.
1) All the coefficients of above equation should have same sign.
2) There should be no missing term.
The above two condition are necessary but not sufficient condition for stability
Routh-Hurwitz Criterion
It states that the system is stable if and only if all the elements is the first column have the same algebraic sign. If all elements are not of the same sign then the number of sign changes of elements in first column equals the number of roots of the characteristic equation in the right half of S-plane.
Consider the following characteristic equation:
a0 Sn + a1 Sn-1 ………….an = 0 where a0,a1,,,,,,,,,,,,,,,,,,,,an have same sign and are non-zero.
Step1 Arrange coefficients in rows
Row1 ao a2 a4
Row2 a1 a3 a5
Step2Find third row from above two rows
Row1 a0 a2 a4
Row2 a1 a3 a5
Row3 a1 a3 a5
a1 = 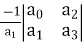 =
= 
a3 = 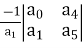 =
= 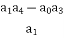
Continue the same procedure to find new rows.
Q1) for the given polynomials below determine the stability of the system
S4+2S3+3S2+4S+5=0
1) Arranging Coefficient in Rows.

S4 | 1 | 3 | 5 |
S3 | 2 | 4 | 0 |
| 1 | 5 | 0 |
| -6 | 0 | 0 |
S0 | 5 | 0 | 0 |
For row S2first term
S2 = 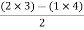 = 1
= 1
For row S2 Second term
S2 = 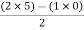 = 5
= 5
For row S1:
S1 = 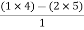 = -6
= -6
For row S0
S0 = 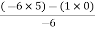 = 5
= 5
As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.
Q2. Using Routh criterion determine the stability of the system with characteristic equation S4+8S3+18S2+16S+S = 0
Sol:- Arrange in rows.
| 1 | 18 | 5 |
S3 | 8 | 16 | 0 |
S2 | 16 | 5 |
|
S1 | 13.5 |
|
|
S0 | 5 |
|
|
For row S2 first element
S1 = 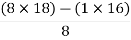 = 16
= 16
Second terms = 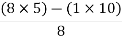 = 5
= 5
For S1
First element = 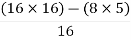 = 13.5
= 13.5
For S0
First element = 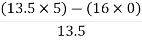 = 5
= 5
As there is no sign change for first column so all roots are is left half of S-plane and hence system is stable.
Special Cases of RouthHurwitz Criterions
- When first element of any row is zero.
In this case the zero is replaced by a very small positive number E and rest of the array is evaluated.
Eg.(1) Consider the following equation
S3+S+2 = 0
| 1 | 1 |
S2 | 0 | 2 |
S1 |
|
|
Replacing 0 by E

S3 | 1 | 1 |
S2 | E | 2 |
S1 | 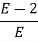 | 0 |
S0 | 2 |
|
Now when E 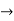 0, values in column 1 becomes
0, values in column 1 becomes
| 1 | 1 |
| E | 2 |
| 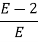 | 0 |
S0 | 2 |
|
Two sign changes hence two roots on right side of S-plans
II) When any one row is having all its terms zero.
When array one row of Routh Hurwitz table is zero, it shown that the X is attests one pair of roots which lies radially opposite to each other in this case the array can be completed by auxiliary polynomial. It is the polynomial row first above row zero.
Consider following example
S3 + 5S2 + 6S + 30
| 1 | 6 |
| 5 |
|
| 0 | 0 |
S0 |
|
|
For forming auxiliary equation, selecting row first above row hang all terms zero.
A(s) = 5S2 e 30
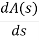 = 10s e0.
= 10s e0.
Again forming Routh array
| 1 | 6 |
S2 | 5 | 30 |
S1 | 10 |
|
S0 | 30 |
|
No sign change in column one the roots of Auxiliary equation A(s)=5s2+ 30-0
5s2+30 = 0
S2 α 6= 0
S = ± j 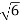
Both lie on imaginary axis so system is marginally stable.
Q3. Determine the stability of the system represent by following characteristic equations using Routh criterion
1) S4 + 3s3 + 8s2 + 4s +3 = 0
2) S4 + 9s3 + 4S2 – 36s -32 = 0
1) S4+3s3+8s2+4s+3=0
S4 | 1 | 8 | 3 |
S3 | 3 | 4 | 0 |
S2 | 6.66 | 3 |
|
S1 | 2.650 | 0 |
|
S0 | 3 |
|
|
No sign change in first column to no rows on right half of S-plane system stable.
S4+9S3+4S2-36S-32 = 0
S4 | 1 | 4 | -32 |
| 9 |
| 0 |
| 8 | -32 |
|
S1 | 0 | 0 |
|
S0 |
|
|
|
Special case II of Routh Hurwitz criterion forming auxiliary equation
A1 (s) = 8S2 – 32 = 0
 = 16S – 0 =0
= 16S – 0 =0
S4 | 1 | 4 | -32 |
S3 | 9 | -36 | 0 |
S2 | 8 | -32 |
|
| 16 | 0 |
|
S0 | -32 |
|
|
One sign change so, one root lies on right half S-plane hence system is unstable.
Q4. For using feedback open loop transfer function G(s) = 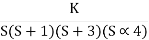
Find range of k for stability
Soln:- Findlay characteristics equation .
CE = 1+G (s) H(s) = 0
H(s) =1 using feedback
CE = 1+ G(s)
1+ 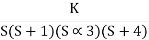 = 0
= 0
S(S+1)(S+3)(S+4)+k = 0
(S2+5)(S2+7Sα12)αK = 0
S4α7S3α1252+S3α7S2α125αK = 0
S4+8S3α19S2+125+k = 0
By Routh Hurwitz Criterion
S4 | 1 | 19 | K |
S3 | 8 | 12 | 0 |
S2 | 17.5 | K |
|
S1 | 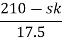 | 0 |
|
S0 | k |
|
|
For system to be stable the range of K is 0< K < .
.
| 1 | 12 | K |
S3 | 4 | 36 |
|
S2 | 3 | K |
|
S1 |  |
|
|
S0 | K |
|
|
Q5. The characteristic equation for certain feedback control system is given. Find range of K for system to be stable.
Soln
S4+4S3α12S2+36SαK = 0
For stability K>0
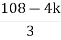 > 0
> 0
K < 27
Range of K will be 0 < K < 27
Relative Stability:-
Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.

The above fig 10.shows the characteristic equation is modified by shifting the origin of S-plane to S1= - .
.
S = Z-S1
After substituting new valve of S =(Z-S1)applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane
Q6. Check if all roots of equation
S3+6S2+25S+38 = 0, have real poll more negative than -1.
Soln:-
S3 | 1 | 25 |
|
S2 | 6 | 38 |
|
S1 | 18.67 |
|
|
S0 | 38 |
|
|

No sign change in first column, hence all roots are in left half of S-plane.
Replacing S = Z-1. In above equation
(Z-1)3+6(Z-1)2+25(Z-1)+38 = 0
Z3+Z23+16Z+18=0
Z3 | 1 | 16 |
Z2 | 3 | 18 |
Z1 | 10 |
|
Z0 | 18 |
|

No sign change in first column roots lie on left half of Z-plane hence all roots of original equation in S-domain lie to left half 0f S = -1
Stability analysis using Nyquist Path :-
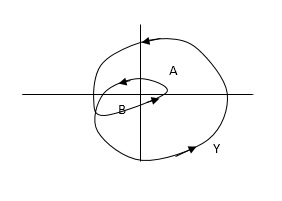
Encircled : A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption :-
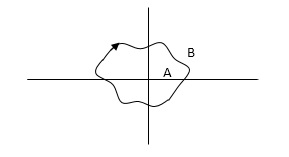
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Further more when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
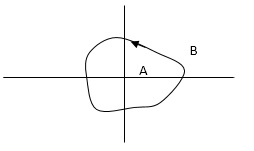
Enclosed :-
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region are

Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is viceversa.
No of encirclements and enclosures :-
 For A line is cut once
For A line is cut once
For B line is cut twice
As it’s overlapping but 2 times in
Same direction
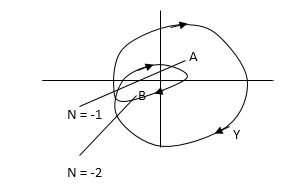
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
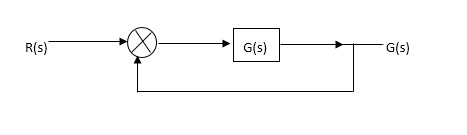
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Inference:-
# OLTF poles is equal to CE poles.
CE = (S + Z’1)( S + Z’2)/( S + P1)( S + P2) - - (3)
CLTF = G(S) –(1) / 1 + G(S) –(3)
= (S + Z1)( S + Z2) / (S + Z’1)( S + Z’2) - - (4)
Inference :-
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
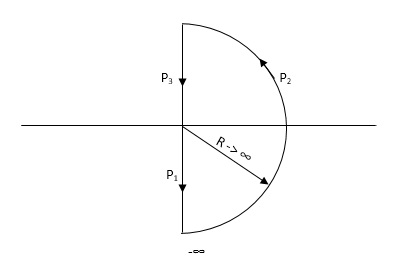
P1W(0 - ∞)
P2RejR ∞
ϴ - π/2 to 0 to + π/2
P3W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE : q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where : Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
- Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important :-
# Open loop System(stable) :- When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
# Open loop system(unstable) :-Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Generalized Point :-
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).
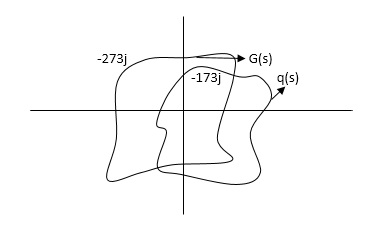
G(S) given then q(S) shift to right side.
The root locus is a graphical produce for determining the stability of a control system which is determined by the location of the poles. The poles are nothing but the roots of the characteristic equation.
Features of Root Locus
- It is symmetrical to the real axis.
- Number of branches of root locus is equal to number of max (poles or zero).
- Starting point (k=0) End point(k—>∞)
(open loop poles) (open loop zeros)
4. A point on the real axis lies on the root locus if number of open loop poles or zero to the right side of that point is odd in number.
5. Value of K anywhere on the root locus is given as
K = 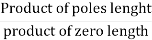
6. I)If poles > zeros then (Þ-z) branches will terminate at ∞ (where k=∞)
II)If Z > P, then (Z-P) branches will start from ∞ (K = 0)
7. When P>Z, (P-Z) branches will terminate at ∞ (open loop zeros). But by which path. So the path is shown by asymptotes and this asymptotes is given by
Asymptote = 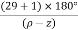 q = o,1,2……(P-Z-1)
q = o,1,2……(P-Z-1)
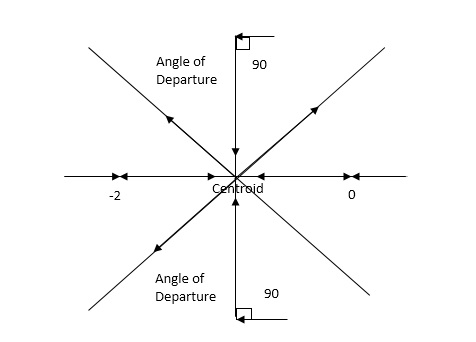
8. There asymptotes intersect the real axis at a single point and this point is known as centroid.
Centroid = 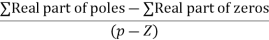
9. Break away and break in point when root locus lie between two poles its called break in point.
Centroid and Breakaway points are not same
Differentials the characteristic equation and equate to zero 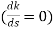
10. Angle of arrival and angle of departure this print is used when the roots are complex.
Angle of departure - for complex poles
Angle of arrival – for complex zero.
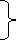 øD =(2q+1) 180° + ø
øD =(2q+1) 180° + ø
øA = (2q+1) 180° - ø ø = ∠Z– ∠P.
11. Intersection of root locus with imaginary axis can be calculated by Routh Hurwitz. By calculating valve of k at intersection point (we can comment about system stability) so by knowing values of k at intersection point (imaginary axis) the valve of s at that point can also be calculated.
Absolutely stable: If the root low (all the branches) lies within the left side of S-plane.
Conditionally Stable:- If some part of the root locus lies on the left half and same
Part on the right of S-plane then it is conditionally stable.
Unstable:- If the root locus lies completely on right side of S-plane then it is unstable.
Construction of Root Locus
Q1. Sketch the root locus for given open loop transfer function G(S) = 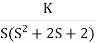 .
.
Soln:- 1) G(s) = 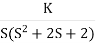
Number of Zeros = 0
Number of polls S = (0, -1+j, -1-j) = (3).
1) Number of Branches = max (P, Z) = max (3, 0) = 3.
2) As there are no zeros in the system so, all branches terminate at infinity.
3) As P>Z, branches terminate at infinity through the path shown by asymptotes
Asymptote = 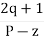 × 180° q = 0, 1, 2………..(p-z-1)
× 180° q = 0, 1, 2………..(p-z-1)
P=3, Z=0.
q= 0, 1, 2.
For q=0
Asymptote = 1/3 × 180° = 60°
For q=1
Asymptote =  × 180°
× 180°
= 180°
For q=2
Asymptote =  × 180° = 300°
× 180° = 300°
Asymptotes = 60°,180°,300°.
4) Asymptote intersects real axis at centroid
Centroid =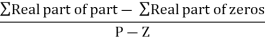
= 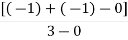
Centroid = -0.66
5) As poles are complex so angle of departure
øD = (2q+1)×180°+ø
ø = ∠Z –∠P.
Calculating ø for S=0
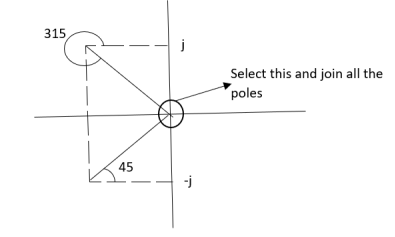
Join all the other poles with S=0
ø = ∠Z –∠P.
= 0-(315°+45°)
= -360°
ØD = (2q + 1)180 + ø.
= 180° - 360°
ØD = -180° (for q=0)
= 180° (for q=1)
=540° (for q=2)
Calculation ØD for pole at (-1+j)
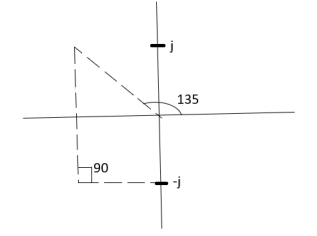
ø = ∠Z –∠P.
= 0 –(135°+90°)
= -225°
ØD = (2q+1) 180°+ø.
= 180-225°
= -45°
ØD = -45° (for q = 0)
= 315° (for q = 1)
= 675° (for q =2)
6) The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.
1+G(s) H (s) = 0
1+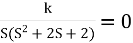
S (S2+2s+2)+k = 0
S3+2s2+2s+K = 0

S3 | 1 | 1 | 0 |
S2 | 2 | K | 0 |
S1 |  | 0 |
|
S0 | K |
|
|
|
|
|
|
For stability 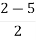 >0. And K > 0.
>0. And K > 0.
0<K<2.
So, when K=2 root locus crosses imaginary axis
S3 + 2S2 + 2S + 2 =0
For k
Sn-1 = 0 n : no. Of intersection
S2-1 = 0 at imaginary axis
S1 = 0
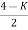 = 0
= 0
K<4
For Sn = 0 for valve of S at that K
S2 = 0
2S2 + K = 0
2S2 + 2 = 0
2(S2 +1) = 0
32 = -2
S = ± j 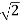
The root locus plot is shown in figure 1.
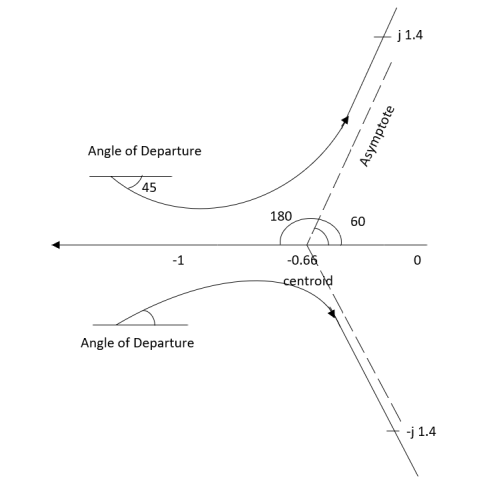
Q2. Sketch the root locus plot for the following open loop transfer function
G(s) = 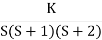
- Number of zero = 0, number of poles = 3
- As P>Z, branches will terminates at infinity
- There are no zeros so all branches will terminate at infinity.
- The path for the branches is shown by asymptote
Asymptote = 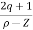 ×180°. q=0,1,………p-z-1
×180°. q=0,1,………p-z-1
P=3, Z=0
q= 0,1,2.
For q = 0
Asymptote =  × 180° = 60.
× 180° = 60.
For q=1
Asymptote =  × 180° = 180°
× 180° = 180°
For q=2
Asymptote =  × 180° = 300°
× 180° = 300°
5. Asymptote intersect real axis at centroid
Centroid = 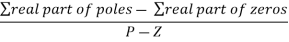
= 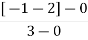 = -1
= -1
6. As root locus lies between poles S= 0, and S= -1
So, calculating breakaway point.
 = 0
= 0
The characteristic equation is
1+ G(s) H (s) = 0.
1+ 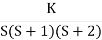 = 0
= 0
K = -(S3+3S2+2s)
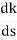 = 3S2+6s+2 = 0
= 3S2+6s+2 = 0
3s2+6s+2 = 0
S = -0.423, -1.577.
So, breakaway point is at S=-0.423
Because root locus is between S= 0 and S= -1
7. The intersection of root locus with imaginary axis is given by Routh criterion.
Characteristics equation is
S3+3S3+2s+K = 0
| 1 | 2 |
S2 | 3 | K |
S1 | 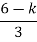 | 0 |
S0 | K |
|
For k
Sn-1= 0 n: no. Of intersection with imaginary axis
n=2
S1 = 0
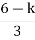 = 0
= 0
K < 6 Valve of S at the above valve of K
Sn = 0
S2 = 0
3S2 + K =0
3S2 +6 = 0
S2 + 2 = 0
S = ±  j
j
The root locus plot is shown in fig. 2.
Q3. Plot the root locus for the given open loop transfer function
G(s) = 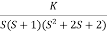
- Number of zeros = 0 number of poles = 4
P = (S=0,-1,-1+j,-1-j) = 4
2. As P>Z all the branches will terminated at infinity.
3. As no zeros so all branches terminate at infinity.
4. The path for branches is shown by asymptote.
Asymptote = 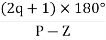 q = 0,1,…..(Þ-z-1)
q = 0,1,…..(Þ-z-1)
q=0,1,2,3. (P-Z = 4-0)
For q=0
Asymptote =  ×180° =45°
×180° =45°
For q=1
Asymptote =  ×180° =135°
×180° =135°
For q=2
Asymptote =  ×180° =225°
×180° =225°
For q=3
Asymptote =  ×180° =315°
×180° =315°
5. Asymptote intersects real axis at unmarried
Centroid = 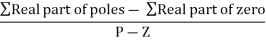
Centroid = 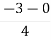 =
= 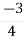 = -0.75
= -0.75
6) As poles are complex so angle of departure is
ØD = (2q+1) ×180 + ø ø = ∠Z –∠P.
A) CalculatingØ for S=0
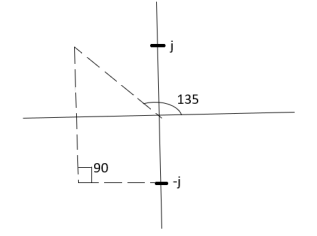
ø = ∠Z –∠P.
= 0 –[315° + 45°]
Ø = -360°
For q = 0
ØD = (2q+1) 180° + Ø
= 180 - 360°
ØD = -180°
b) Calculating Ø for S=-1+j
ø = ∠Z –∠P.
= 0-[135° + 90° + 90°]
Ø = -315°
For q=0
ØD= (2q+1) 180° +Ø
= 180° -315°
ØD = -135°
ØD for S=1+j will be ØD = 45°
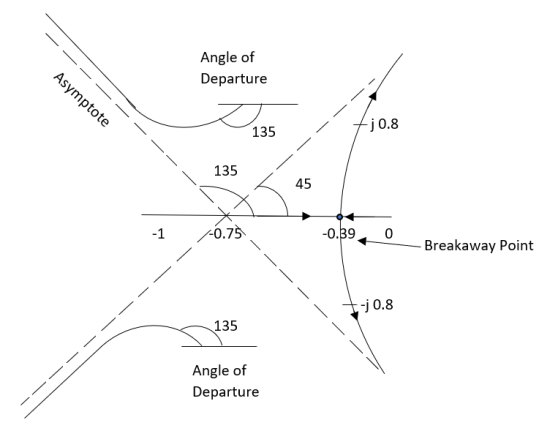
7) As the root locus lie between S=0 and S=-1
So, the breakaway point is calculated
1+ G(s)H(s) = 0
1+ 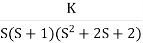 = 0
= 0
(S2+S)(S2 +2S+2) + K =0
K = -[S4+S3+2s3+2s2+2s2+2s]
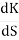 = 4S3+9S2+8S+2=0
= 4S3+9S2+8S+2=0
S = -0.39, -0.93, -0.93.
The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-1
8) Intersection of root locus with imaginary axis is given by Routh Hurwitz
I + G(s) H(s) = 0
K+S4+3S3+4S2+2S=0

S4 | 1 | 4 | K |
S3 | 3 | 2 |
|
S2 | 3.33 | K |
|
S1 | 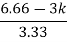 |
|
|
S0 | K |
|
|
For system to be stable
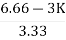 >0
>0
6.66>3K
0<K<2.22.
For K = 2.22
3.3352+K =0
3.3352+ 2.22 = 0
S2 = -0.66
S = ± j 0.816.
The root locus plot is shown in figure 3.
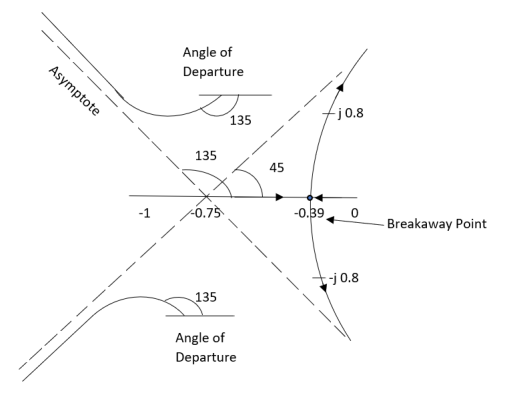
Figure-3
Q4. Plot the root locus for open loop system
G(s) = 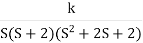
1) Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j.
2) As no zeros are present so all branches terminated at infinity.
3) As P>Z, the path for branches is shown by asymptote
Asymptote = 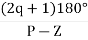
q = 0,1,2……p-z-1
For q = 0
Asymptote = 45°
q=1
Asymptote = 135°
q=2
Asymptote = 225°
q=3
Asymptote = 315°
4) Asymptote intersects real axis at centroid.
Centroid = 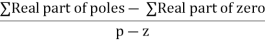
= 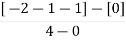
Centroid = -1.
5) As poles are complex so angle of departure is
ØD=(2q+1)180° + Ø
ø = ∠Z –∠P
= 0-[135°+45°+90°]
= 180°- 270°
ØD = -90°
6) As root locus lies between two poles so calculating point. The characteristic equation is
1+ G(s)H(s) = 0
1+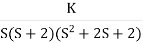 = 0.
= 0.
K = -[S4+2S3+2S2+2S3+4S2+4S]
K = -[S4+4S3+6S2+4S]
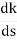 = 0
= 0
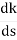 = 4s3+12s2+12s+4=0
= 4s3+12s2+12s+4=0
S = -1
So, breakaway point is at S = -1
7) Intersection of root locus with imaginary axis is given by Routh Hurwitz.
S4+4S3+6S2+4s+K = 0

S4 | 1 | 6 | K |
S3 | 4 | 4 |
|
S2 | 5 | K |
|
S1 | 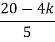 |
|
|
S0 | K |
|
|
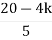 ≤ 0
≤ 0
K≤5.
For K=5 valve of S will be.
5S2+K = 0
5S2+5 = 0
S2 +1 = 0
S2 = -1
S = ±j.
The root locus is shown in figure 4.
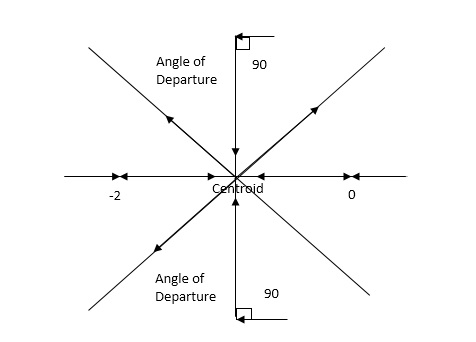
Figure-4
Q5. Plot the root locus for open loop transfer function G(s) = 
- Number of zeros = 0. Number of poles = 4 located at S=0, -3, -1+j, -1-j.
- As no. Zero so all branches terminate at infinity.
- The asymptote shows the both to the branches terminating at infinity.
Asymptote = 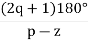 q=0,1,….(p-z).
q=0,1,….(p-z).
For q = 0
Asymptote = 45
For q = 1
Asymptote = 135
For q = 2
Asymptote = 225
For q = 3
Asymptote = 315
(4). The asymptote intersects real axis at centroid.
Centroid = ∑Real part of poles - ∑Real part of zero / P – Z
= [-3-1-1] – 0 / 4 – 0
Centroid = -1.25
(5). As poles are complex so angle of departure
φD = (29 + 1)180 + φ
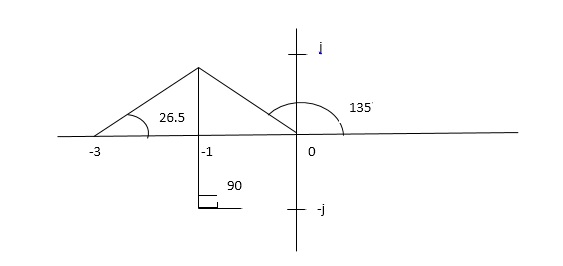
ø = ∠Z –∠P.
= 0 – [ 135 + 26.5 + 90 ]
= -251.56
For q = 0
φD = (29 + 1)180 + φ
= 180 – 215.5
φD = - 71.56
(6). Break away point dk / ds = 0 is at S = -2.28.
(7). The intersection of root locus on imaginary axis is given by Routh Hurwitz.
1 + G(S)H(S) = 0
K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0
S4 1 8 K
S3 5 6
S2 34/5 K
S1 40.8 – 5K/6.8
K ≤ 8.16
For K = 8.16 value of S will be
6.8 S2 + K = 0
6.8 S2 + 8.16 = 0
S2 = - 1.2
S = ± j1.09
The plot is shown in figure 5.
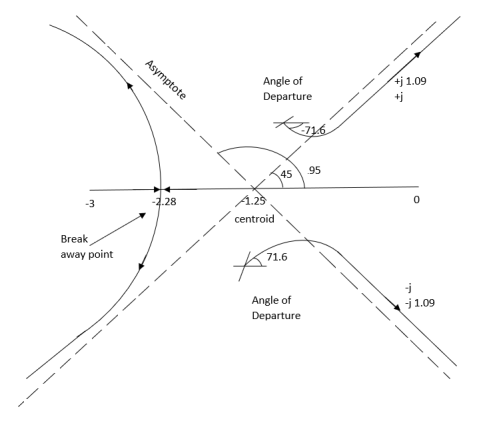
Figure-5
Q.6. Sketch the root locus for open loop transfer function.
G(S) = K(S + 6)/S(S + 4)
- Number of zeros = 1(S = -6)
Number of poles = 2(S = 0, -4)
2. As P > Z one branch will terminate at infinity and the other at S = -6.
3. For Break away and breaking point
1 + G(S)H(S) = 0
1 + K(S + 6)/S(S + 4) = 0
Dk/ds = 0
S2 + 12S + 24 = 0
S = -9.5, -2.5
Breakaway point is at -2.5 and Break in point is at -9.5.
4. Root locus will be in the form of a circle. So finding the centre and radius. Let S = + jw.
G( + jw) = K( + jw + 6)/( + jw)( + jw + 4 ) = +- π
Tan-1 w/ + 6 - tan-1 w/ – tan-1 w / + 4 = - π
Taking tan of both sides.
w/ + w/ + 4 / 1 – w/ w/ + 4 = tan π + w / + 6 / 1 - tan π w/ + 6
w/ + w/ + 4 = w/ + 6[ 1 – w2 / ( + 4) ]
(2 + 4)( + 6) = (2 + 4 – w2)
2 2 + 12 + 4 + 24 = 2 + 4 – w2
22 + 12 + 24 = 2 – w2
2 + 12 – w2 + 24 = 0
Adding 36 on both sides
( + 6)2 + (w + 0)2 = 12
The above equation shows circle with radius 3.46 and centre (-6, 0) the plot is shown in figure.6.

Figure-6
It helps to make an unstable system to become a stable system by various techniques. In compensation we are able to change the transfer function of the system as we can introduce the poles and zeros in the system to compensate the instability occurring. This in turn increases the accuracy of the system.
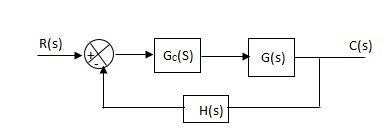
i) Cascade Compensation: The controller gain Gc(s) is connected in series with the system.
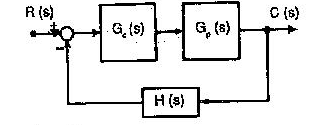
Fig: Cascade Compensation
Ii) Feedback Compensation: The controller gain Gc(s) is connected in feedback with the system.
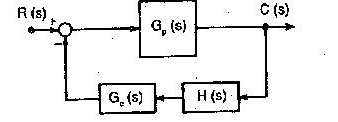
Fig: Feedback Compensation
Iii) Load Compensation: The controller gain Gc(s) is connected at the output in the system.
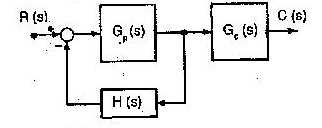
Fig: Load Circuit Compensation
Iv) Input Circuit Compensation: The controller gain Gc(s) is connected at the input in the system.
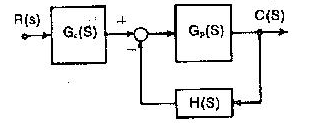
Fig: Input circuit compensation
Phase – Lead Compensation :-
The phase of output voltage leads the phase of input voltage for the applied sinusoidal input. The circuit diagram is shown below. The transfer function is given as,
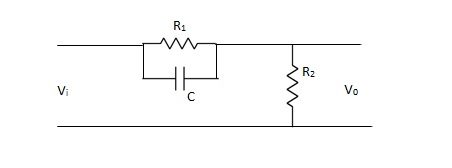
Vo/Vi = α(1 + ST)/(1 + S α T)
Where, α = R2/R1 + R2 and α< 1
T = R1C
w = 1/T lower corner frequency due to zero.
w = 1/ αT upper corner frequency due to pole.
Mid frequency is given as,
wm = 1/T√ α
The maximum phase lead angle is φm
Φm = tan-1(1- α)/2√α = Sin-11- α/1 + α
Phase Lag Compensation :-
The phase of the output voltage lags the phase of the input voltage for applied sinusoidal input. The circuit diagram is shown below,
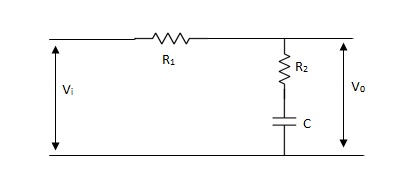
Vo/Vi = 1 + ST/1 + SβT
Where, β = R1 + R2/R2, β> 1
T = R2C
w = 1/T upper corner frequency due to zero
w= 1/βT lower corner frequency due to pole
The mid frequency wm,
wm = 1/T√β
The maximum phase lead angle Φm
Φm = tan-11- β/2 √β
= sin-11 – β/1 + β
Phase Lead Network Phase Lag Network
1>. It is used to improve the It is used to improve the
Transient response. Steady state response.
2>. It acts as a high pass filter. It acts as a low pass filter.
3>. The system becomes fast as The Bandwidth decreases
Bandwidth increases as rise through rise time the speed
Time decreases. is slow.
4>. As the circuit acts as Signal to noise ratio is higher as it a differentiator, signal to acts as integrator.
Noise ratio is poor.
5>. Maximum peak overshoot It reduces steady state error thus
Is reduced. improve the steady state accuracy
Phase Lag-Lead Network:
To overcome the disadvantages of lead and lag compensation, they are used together. As lead compensation does not provide phase margin but has fast response and lag compensation stabilize the system but does not provide enough bandwidth.
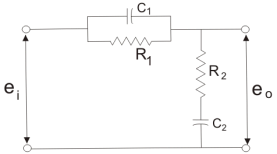
Fig: Lag-Lead Compensation
eo/ei = (1 + αST1)/(1 + S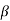 T2)
T2)
Where, αT1 = R1C1
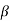 T2=R2C2
T2=R2C2
We can say in the lag-lead compensation pole is more dominating than the zero and because of this lag-lead network may introduces positive phase angle to the system when connected in series.
Effects of controller are viewed on time response and stability.
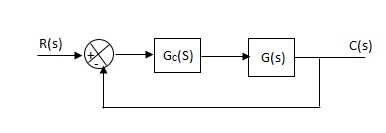
Gc(S) = TF of the controller
G(S) = OLTF without controller
G’(S) = Gc(S).G(S)
= OLTF with controller
(1). Proportional Controller :-
Proportional means scalar Multiplier.
Gc(S) = Kp Stability can be controlled
Q. G(S) = 1/S(S + 8)
CLTF = 1/S2 + 8S + 1
w2n = 1
wn = 1
2ξWn = 8
ξ = 4
ξ>/1 so, overdamped.
Now introducing Gc(S) = K
G’(S) = Kp/S(S + 8)
CLTF = Kp/S2 + 8S + Kp
wn = √Kp
2 ξwn = 8
ξ = 4/√Kp
If,
Kp = 16; ξ = 1; critically damped
Kp> 16; ξ< 1; undamped
Kp< 16; ξ> 1; overdamped
(2). Integral controller:-
The transfer function of this controller is
Gc(S) = Ki/S
Integral controller are used to improve the steady state response or reduce the steady state error.

G’(S) = Gc(S).G(S)
G(S) = 1/S + 5, Gc(S) = Ki/S
G’(S) = Ki/S(S + 5). After applying the Gc(S) the type of system is increasing and hence, the steady state error is decreasing (Refer Time Response).
Disadvantage :-
By using integral controller the stability of closed loop system decreases.
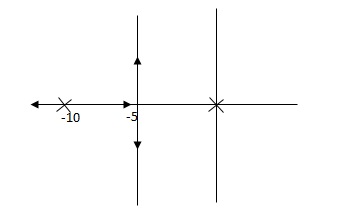
G(S) = 1/S + 5
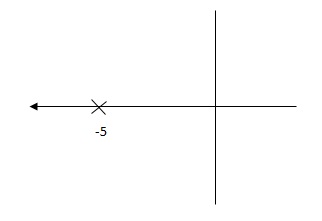
G’(S) = Ki/S(S + 5)
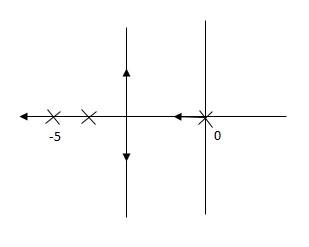
Fig(1), is more stable than (2) as more the away the pole from origin (imaginary axis) more is the stability.
Q. G(S) = 1/(S + 5)(S + 10)
G’(S) = Kp/S(S + 5)(S + 10)
G(S) = 1/(S + 5)(S + 10)
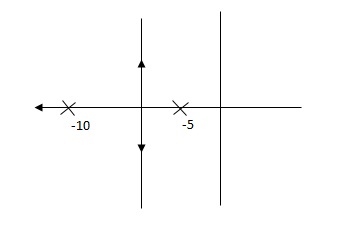
G’(S) = Ki/S(S + 5)(S + 10)
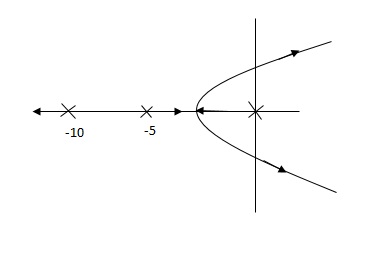
So, (b), is less stable at root locus lies on the R.H.S,
(3). Derivative Controller :-
Gc(S) = Kd(S)
They are used to improve the stability.
G’(S) = KdS/S2(S + 10)
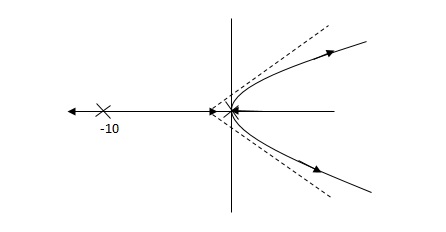
(b) is stable i.e. more stable than the (a).
Disadvantage :-
It increases the steady state i.e. o/p will not track the input at steady state.
(4). Proportional Plus Integral [PI] controller :-
Gc(S) = KpS + Ki/S
The steady state error will decrease and the stability will depend on Kp i.e. if Kp is increased/decreased than according to it stability will change(Kpα stability).
Used to reduce ess without much affecting the stability.
(5). Proportional Plus Derivative Controller :-
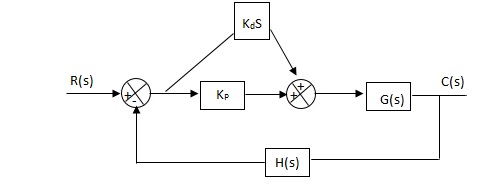
Used to improve the stability without affecting much the steady state error.
(6). PID controller :-
Gc(S) = Kp + Ki/S + KdS
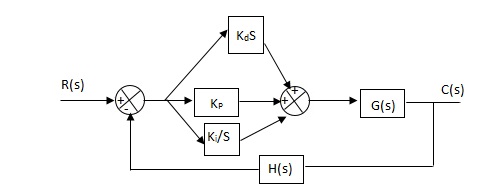
It improves the stability. It decreases the steady state error and both are proportional to Kp.
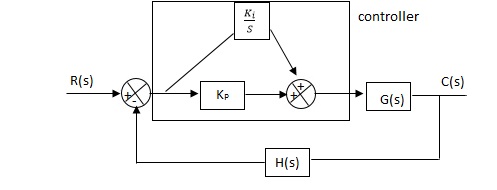
Q.The block diagram of a system using PI controllers is shown in the figure. Calculate :
(a). The steady state without and with controller for unit step input?
(b). Determine TF of newly constructed sys. With controller so, that a CL Poles is located at -5?

(a). Without :
C(S)/R(S) = 0.2/(S + 1)
C(S) = R(S) 0.2/(S + 1) + 0.2
For unit step
Ess = 1/1 + Kp
Kp = lt G(S)
S 0
= lt 0.2/(S + 1)
S 0
Kp = 0.2
Ess = 1/1.2 = 5/6 = 0.8
(b). With controller :
Gc(S) = Kp + Ki/S
G’(S) = Gc(S).G(S)
= ( Kp + Ki/S )0.2/(S + 1)
= (KpS + Ki)0.2/S(S + 1)
Ess = 1/1 + Kp = 0
So, the value of ess is decreased.
(b). Given
Kpi/Kp = 0.1
G’(S) = (Kp + Ki/S)(0.2/S + 1)
= (KpS + Ki)0.2/S(S + 1)
As a pole is to be added so, we have to examine the CE,
1 + G’(S) = 0
1 + (Kp + Ki)0.2/S(S + 1) = 0
S2 + S + 0.2KpS + 0.2Ki = 0
S2 + (0.2Kp + 1)S + 0.2Ki = 0
Given,
Kpi = 0.1Ki
Kp = 10Ki
S2 + (2Ki + 1)S + 0.2Ki = 0
Pole at S = -5
25 + (2Ki + 1)(-5) + 0.2Ki = 0
-10Ki – 5 + 25 + 0.2Ki = 0
-9.8Ki = -20
Ki = 2.05
Kp = 10Ki
= 20.5
Now,
G’(S) = (KpS + Ki)(0.2)/S(S + 1)
= (20.5S + 2.05)(0.2)/S(S + 1)
G’(S) = 4.1S + 0.41/S(S + 1)
Q.The block diagram of a system using Pd controller is shown, the PD is used to increase ξ to 0.8. Determine the T.F of controller?
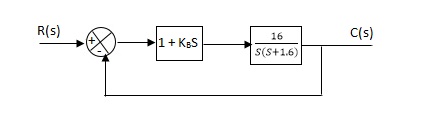
(1). Kp = 1
Without controller:-
C(S)/R(S) = 16/S2 + 1.6S + 16
wn = 4
2 ξwn = 16
ξ = 1.6/2 x 4 = 0.2
(b). With derivative :-
ξS = 0.2 to 0.8
Undamped to critically damped,
G’(S) = (1 + KdS)(16)/(S2 + 1.6S)
CE:
S2 + 1.6S + 16(1 + KdS) = 0
S2 + (1.6 + Kd)S + 16 = 0
2 ξwn = 1.6 + Kd1.6
wn = 4
ξS = 0.8
2 x 4 x 0.8 = 1.6 + Kd1.6
6.4 – 1.6 = Kd1.6
4.8/16 = Kd
Kd = 0.3
TF = (1 + 0.3S)16/S(S + 16)