Unit-1

Introduction

1.1 Block Diagram of Digital Communication System

The elements which form a digital communication system is represented by the following block diagram for the ease of understanding.

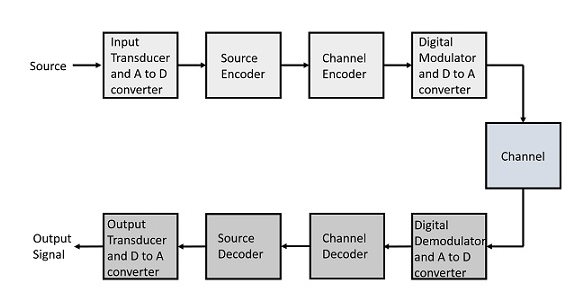
Fig 1 Elements of Digital Communication System

Following are the sections of the digital communication system.

Source

The source can be an analog signal. 

Example: A Sound signal

Input Transducer

This is a transducer which takes a physical input and converts it to an electrical signal. This block also consists of an analog to digital converter where a digital signal is needed for further processes.

A digital signal is generally represented by a binary sequence.

Source Encoder

The source encoder compresses the data into minimum number of bits. This process helps in effective utilization of the bandwidth. It removes the redundant bits unnecessary excess bits, i.e. ,zeroes.

Channel Encoder

The channel encoder, does the coding for error correction. During the transmission of the signal, due to the noise in the channel, the signal may get altered and hence to avoid this, the channel encoder adds some redundant bits to the transmitted data. These are the error correcting bits.

Digital Modulator

The signal to be transmitted is modulated here by a carrier. The signal is also converted to analog from the digital sequence, in order to make it travel through the channel or medium.

Channel

The channel or a medium, allows the analog signal to transmit from the transmitter end to the receiver end.

Digital Demodulator

This is the first step at the receiver end. The received signal is demodulated as well as converted again from analog to digital. The signal gets reconstructed here.

Channel Decoder

The channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits. This addition of bits helps in the complete recovery of the original signal.

Source Decoder

The resultant signal is once again digitized by sampling and quantizing so that the pure digital output is obtained without the loss of information. The source decoder recreates the source output.

Output Transducer

This is the last block which converts the signal into the original physical form, which was at the input of the transmitter. It converts the electrical signal into physical output.

Output Signal

This is the output which is produced after the whole process.

Key takeaway

 The channel decoder, after detecting the sequence, does some error corrections. The distortions which might occur during the transmission, are corrected by adding some redundant bits.

1.2 Advantages of Digital communication system over Analog communication systems

1.3 Sampling theorem

Sampling is defined as, “The process of measuring the instantaneous values of continuous-time signal in a discrete form.”

Sample is a piece of data taken from the whole data which is continuous in the time domain.

When a source generates an analog signal and if that has to be digitized, having 1s and 0s i.e., High or Low, the signal has to be discretized in time. This discretization of analog signal is called as Sampling.

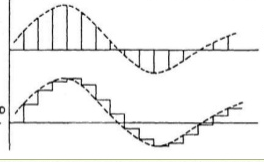
The following figure indicates a continuous-time signal x (t) and a sampled signal xs (t). When x (t) is multiplied by a periodic impulse train, the sampled signal xs (t) is obtained.

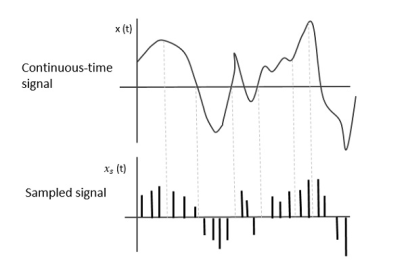
Fig 2 Sampled Signal

Sampling Rate

To discretize the signals, the gap between the samples should be fixed. That gap can be termed as a sampling period Ts.

Sampling Frequency=1/Ts=fs

Where,

Sampling frequency is the reciprocal of the sampling period. This sampling frequency, can be simply called as Sampling rate. The sampling rate denotes the number of samples taken per second, or for a finite set of values.

Nyquist Rate

Suppose that a signal is band-limited with no frequency components higher than W Hertz. That means, W is the highest frequency. For such a signal, for effective reproduction of the original signal, the sampling rate should be twice the highest frequency.

Which means,

fS=2W

Where,

This rate of sampling is called as Nyquist rate.

Sampling Theorem

The sampling theorem, which is also called as Nyquist theorem, delivers the theory of sufficient sample rate in terms of bandwidth for the class of functions that are bandlimited.

The sampling theorem states that, “a signal can be exactly reproduced if it is sampled at the rate fs which is greater than twice the maximum frequency W.”

Let us consider a band-limited signal, i.e., a signal whose value is non-zero between some –W and W Hertz.

Such a signal is represented as x(f)=0 for ∣f∣>W

For the continuous-time signal x (t), the band-limited signal in frequency domain, can be represented as shown in the following figure.

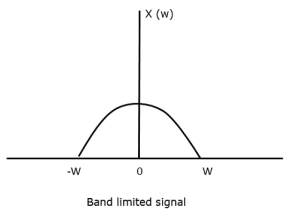
Fig 3 Band limited Signal

If the signal x(t) is sampled above the Nyquist rate, the original signal can be recovered, and if it is sampled below the Nyquist rate, the signal cannot be recovered.

The following figure explains a signal, if sampled at a higher rate than 2w in the frequency domain.

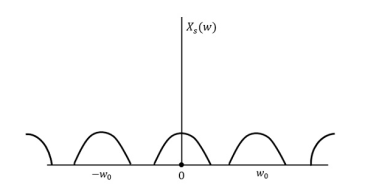
Fig 4 Fourier Transform of xs(t)

The above figure shows the Fourier transform of a signal xs (t).

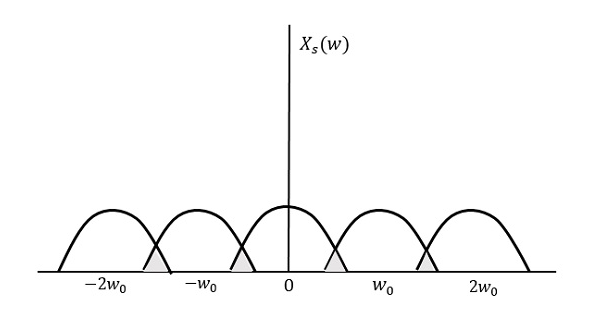
If  fs<2W

The resultant pattern will look like the following figure.

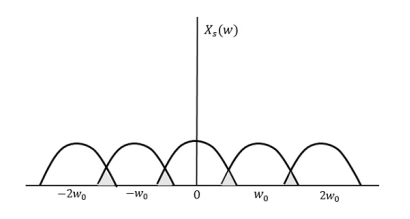
Fig 5 Output Waveform

Here, the over-lapping of information is done, which leads to mixing up and loss of information. This unwanted phenomenon of over-lapping is called as Aliasing.

Aliasing

Aliasing can be referred to as “the phenomenon of a high-frequency component in the spectrum of a signal, taking on the identity of a low-frequency component in the spectrum of its sampled version.”

Key Takeaways:

Examples:

The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].

Solution:

We know,

X[n] =x(nT)

      = cos(200πnT)

      = cos(2πn/3) , where n= -1,0,1,2……

The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.

Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of:

X(t) = 1+ sin(2000πt) + cos (4000πt)

Solution:

The frequencies are 0, 2000π and  4000π.

The Nyquist frequency is   4000π rad/s and the Nyquist rate is 8000π rad/s.

Consider an analog signal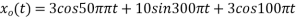

Find the Nyquist rate?

Solution.

The frequency in the analog signal

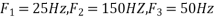
The largest frequency is

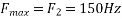
The Nyquist rate is

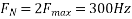
The analog signal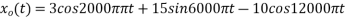

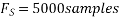
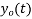
Using a sampling rate

. What is discrete time signal obtained after sampling?

What is analog signal

we can reconstruct from the samples if we use ideal interpolation?

Solution.

For

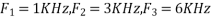
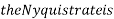
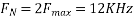
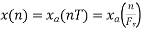
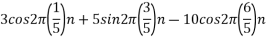
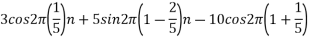
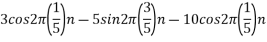
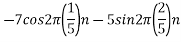
For 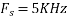  ,the folding frequency is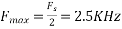

Hence 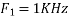is not effected by aliasing

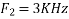Is changed by the aliasing effect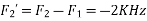

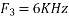Is changed by the aliasing effect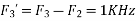

So that normalizing frequencies are

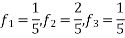
The analog signal that we can recover is

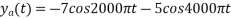
Which is different than the original signal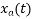

For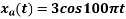 

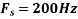
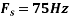
If

, what is the discrete time signal after sampling?

If

, what is the discrete time signal after sampling?

Solution. a.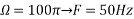

The minimum sampling rate is

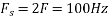
And the discrete time signal is

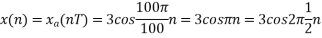
b. if 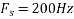  , the discrete time signal is

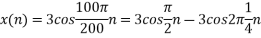
c. If Fs=75Hz , the discrete time signal is

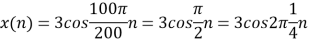
d. For the sampling rate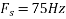

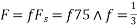   in part in (c). Hence

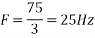
So, the analog sinusoidal signal is

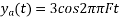
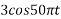
Suppose a continuous-time signal  x(t) = cos (Ø0t) is sampled at a sampling frequency of 1000Hz to produce x[n]: x[n] = cos(πn/4)

Determine 2 possible positive values of Ø0, say, Ø1 and Ø2. Discuss if cos(Ø1t) or cos(Ø2t) will be obtained when passing through the DC converter.

Solution:

Taking T= 1/1000s

cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000)

Ø1 is easily computed as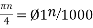           

Ø1 = 250π

Ø2 can be obtained by noting the periodicity of a sinusoid:

Ø2n/1000)

Ø2 = 2250π

1.4 Signal reconstruction in time domain

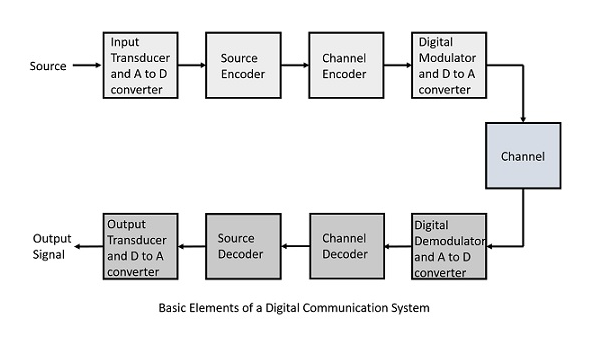
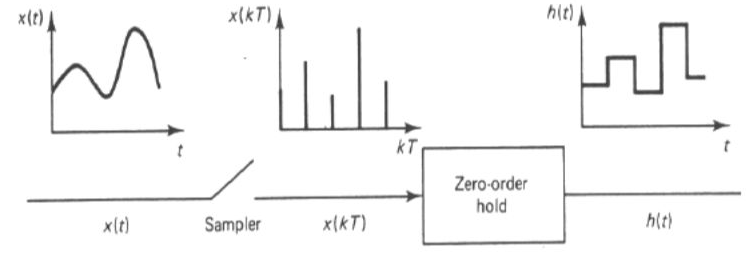
Fig 6 (a) Sampler (b) Output

The sampled data signal is modified by the controller. The hold circuit than converts the signal to analog form. The simplest hold circuit is ZOH (zero order hold) in which the reconstructed signal acquires the same value as the last received sample for the entire sampling period.

The basic sampler is shown in above figure (a) and output in figure (b). The high frequency signal present in the reconstructed signal is filtered by the controller elements which are the low pass in frequency behaviour.

The first or higher order holds have no advantage over the ZOH. In the first order hold the last two signal samples are used to reconstruct the signal for the current sampling period.

Data hold is a process of generating a continuous-time signal h(t) from a discrete time signal x(kT). The signal x(kT) can be approximated by a polynomial as

h(kT+)=an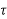n+an-1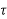n-1+….+a1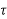+a0       0≤ 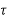≤ T

h(kT)=x(kT)

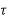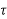h(kT+)=ann+an-1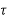n-1+….+a1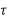+x(kT)

If the data hold circuit is an nth order polynomial it is called as nth order hold circuit.

Zero Order Hold (ZOH)

If n=0 in above equation the zero-order hold is obtained.

h(kT+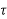)= x(kT)                                                         0≤ 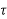≤ T    k=0,1,2,3…….

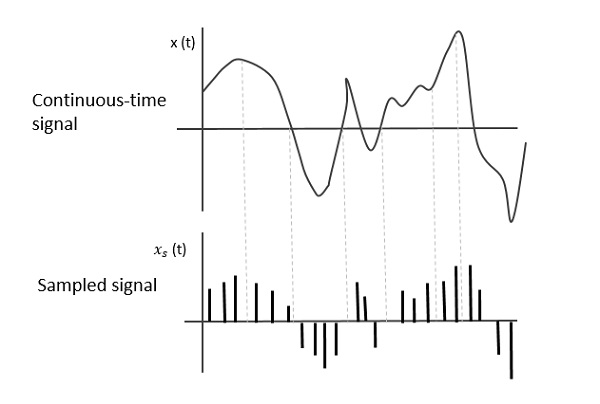
                                                             Fig 7 Zero Order Hold

h(t)=x(0)[u(t)-u(t-T)]+x(t)[u(t-T)-u(t-2T)]+x(2T)[u(t-2T)-u(t-3T)]……..

       =

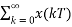
Taking Laplace transform of above equation we get

L[u(t-kT)] =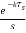

L[h(t)]=L{}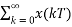

H(s)==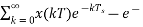

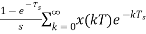
Gho(s)=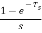

X*(s)=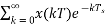

The transfer function of ZOH is Gho(s)=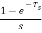

Key takeaway

The transfer function of ZOH is Gho(s)=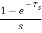

1.5 Practical and Flat Top Sampling

During transmission, noise is introduced at top of the transmission pulse which can be easily removed if the pulse is in the form of flat top. Here, the top of the samples are flat i.e. they have constant amplitude. Hence, it is called as flat top sampling or practical sampling. Flat top sampling makes use of sample and hold circuit.

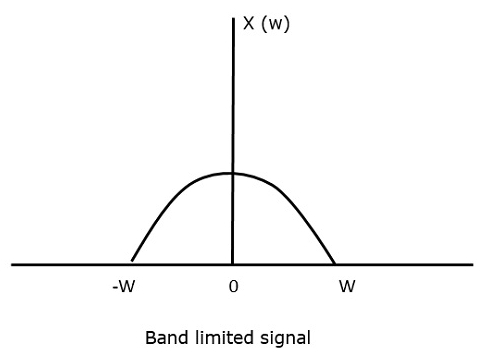
Fig 8 Flat top Sampled Signal

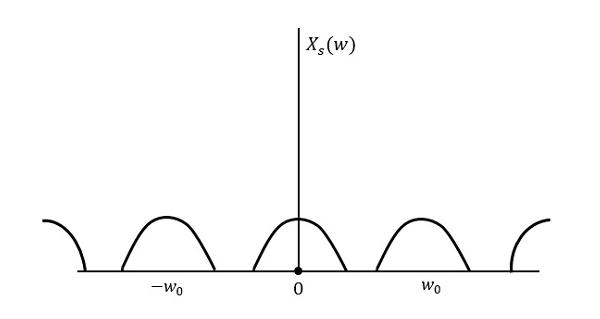
Fig 9 Flat top signal obtained after convolution

The sampled signal can be obtained by convolution of rectangular pulse p(t) with ideally sampled signal say yδ(t) as shown in the diagram above

y(t) = p(t) x yδ(t)

Taking F.T of above signal we get

From convolution

Key takeaway

1.6 Sampling of Band-pass Signal

 The bandpass signal x(t) which maximum bandwidth is 2W can be completely represented into and recovered from its samples if it is sampled at the minimum rate of twice the bandwidth. The spectrum is centred around frequency fc. The bandwidth is 2W. Thus, the frequencies in the bandpass signals are from fc-W to fc+W. The bandpass signal is represented in its in-phase and quadrature components.

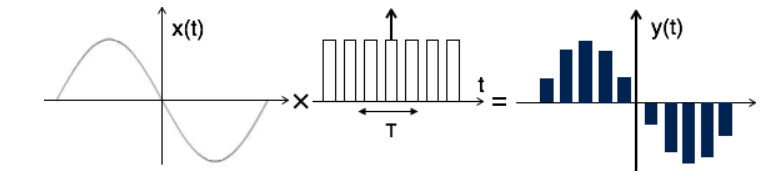
Fig 10 Spectrum of Bandpass Signal

x1(t) = in-phase component

xQ(t) = Quadrature component

Then signal x(t) can be written as

x(t) = x1(t)cos(2πfct)-xQ(t) sin (2 πfct) 

The spectrum of the above signal is in between -W to +W. This is shown in below figure

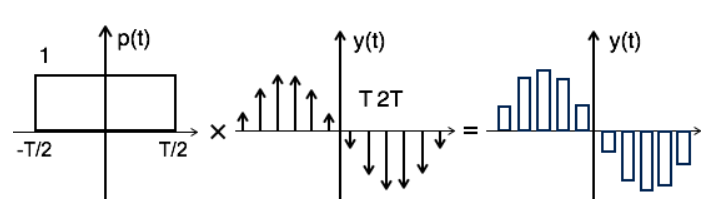
Fig 11 Spectrum of in-phase and quadrature components of Bandpass signal x(t)

The reconstructed signal is then given by

X(t)= 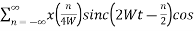πfc(t-)]

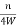From above equation we can conclude that

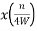= x(nTs)

Ts =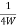

Key takeaway

For bandpass signal with bandwidth 2W the minimum sampling rate is twice the bandwidth.

1.7 Aliasing Problem

1.8 Uniform and Non-uniform quantization

Quantization noise is a model of quantization error introduced by quantization in the analog-to-digital conversion (ADC). It is a rounding error between the analog input voltage to the ADC and the output digitized value. The noise is non-linear and signal-dependent.

There are two types of Quantization - Uniform Quantization and Non-uniform Quantization.

The type of quantization in which the quantization levels are uniformly spaced is termed as a Uniform Quantization.

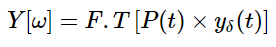
Fig 12 Uniform Quantization

The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as a Non-uniform Quantization.

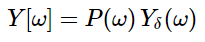
Fig 13 Non-Uniform Quantization

Key takeaway

The type of quantization in which the quantization levels are uniformly spaced is termed as a Uniform Quantization. The type of quantization in which the quantization levels are unequal and mostly the relation between them is logarithmic, is termed as a Non-uniform Quantization.

1.9 Signal to Quantization ratio of Quantized Signal.

The signal-to-noise ratio is

SNR = average signal power /average noise power

For uniform quantization noise

average signal power ≈ am2p (a ≈ 1 2 )

quantization error ≈ 1/3 (mp/L)2

 SNR ≈ cL2 = c22m where m is the number of bits in the PCM sample, so L = 2m. c is a constant

SNR grows exponentially with the number of bits.

If we measure SNR in dB,

SNRdB = 10 log10(c22m) = 10 log10(c) + 2m log102 = (α + 6m)dB

where α = 10 log10 c.

Key takeaway

Increasing n by one bit improves SNR by 6 dB! One bit quadruples SNR.

References

1. “Communication Systems”, Simon Haykin, Wiley publication, 4th Edition, 2004

2. “Digital Communication Fundamentals and Applications”, Bernard Sklar, Pearson

Education India, 2nd Edition, 2009

3. “Modern Electronic Communication”, Miller Gary M, Prentice-Hall, 6th Edition, 1999

4. “Digital Communications”, John Proakis, Tata Mc Graw Hill, 5th Edition, 2007

5. “Electronic Communication Systems, Fundamentals Through Advanced”, Wayne Tomsi, Pearson Education, 4th Edition, 2001