Unit-3
Storage strategies
Indexing is a technique for data structure that helps you to access information from a database file quickly. An Index is a small table of two columns only. The first column consists of a copy of a table's primary or candidate key. The second column includes a series of pointers to hold the disc block address where that particular key value is located.
Indexing is a way of maximizing a database's output by minimizing the amount of disc access needed when processing a question. It is a technique for data structure that is used to find and access the data in a database easily.
Using a few database columns, indexes are established.
- The first column is the Search key, which includes a copy of the table's primary or candidate key. In order for the corresponding data to be accessed easily, these values are stored in sorted order.
- The second column is the Data Reference or Pointer, which includes a series of pointers that hold the disc block address where you can find the particular key value.
Indexing has different attributes:
● Access Types: This refers to the access type, such as value-based quest, access to the range, etc.
● Access Time: This refers to the time taken to locate a single element of data or a collection of elements.
● Insertion Time: It relates to the time it takes to find a suitable space and insert new data.
● Deletion Time: It takes time to find and delete an object and to update the layout of the index.
● Space Overhead: It refers to the extra space that the index takes.
Types of indexes
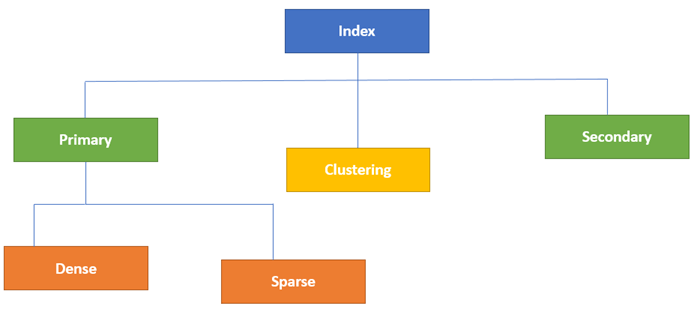
Fig 1: types of database
- Primary index
The Primary Index is an ordered file with two fields and a fixed length scale. The first field is the same as the primary key, and the second field is pointed to that particular block of information. In the primary index, the relationship between the entries in the index table is always one-to-one.
Main DBMS indexing is also further split into two forms :
- Dense
- Sparse
- Dense index
In a dense index, for each search key valued in the database, a record is generated. This helps you to search more easily, however more space is required to store index records. Method records include the value of the search key in this index and point to the actual record on the disc.
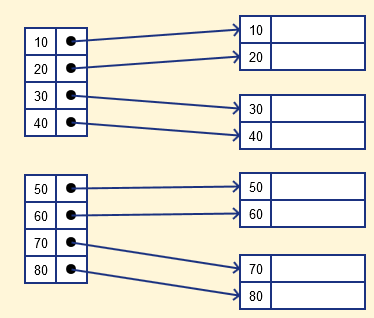
Fig 2: dense index
- Sparse index
It is an index record that only exists in the file for some of the values. The Sparse Index helps you solve the problems of DBMS Dense Indexing. A number of index columns store the same data block address in this form of indexing technique, and the block address will be fetched when data needs to be retrieved.
However, for only those search-key values, sparse Index stores index records. It requires less space, less overhead maintenance for insertion, and deletions, but compared to the dense index for locating records, it is slower.
The database index below is an example of the Sparse Index
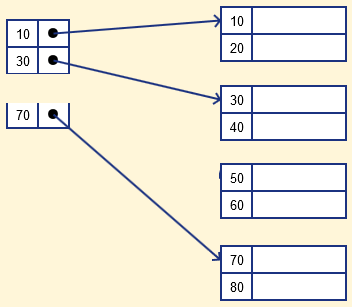
Fig 3: sparse index
2. Clustering index
The records themselves are stored in the index in a clustered index, and not the pointers. On non-primary key columns, the Index is often generated, which may not be unique for each record.
You can group two or more columns in such a situation to get unique values and create an index called the Clustered Index. This helps you locate the record faster as well.
Example :
Suppose a business has many staff in each department. Suppose we use a clustering index, where all employees within a single cluster who belong to the same Dept ID are considered, and index pointers point to the entire cluster. Dept Id is a non-unique key here.
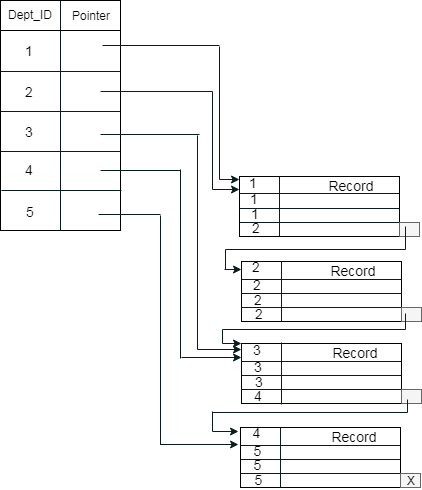
Fig 4: example of cluster index
3. Secondary index
In DBMS, a secondary index can be created by a field that has a specific value for each record and should be a candidate key. It is also known as an index for non-clustering.
To reduce the mapping size of the first level, this two-level database indexing technique is used. A wide range of numbers is chosen for the first level because of this; the mapping size still remains small.
In secondary indexing, another degree of indexing is added to reduce the mapping scale. The huge range for the columns is initially chosen in this process, so that the mapping scale of the first level becomes small. Each range is then further split into smaller ranges.
The first level mapping is stored in the primary memory, so that the fetching of addresses is easier. In the secondary memory, the second level mapping and actual data are stored (hard disk).
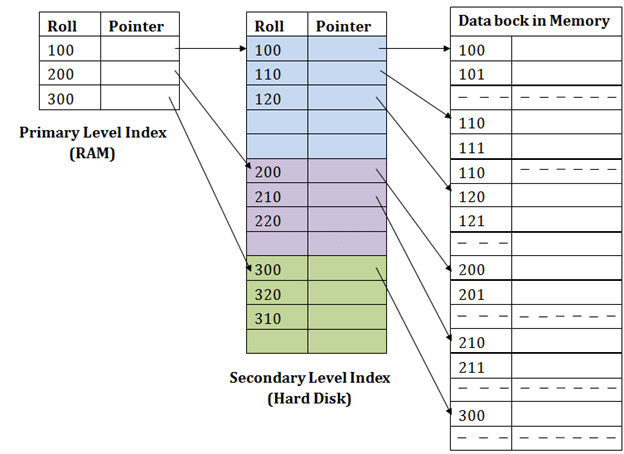
Fig 5: secondary index
Let’s understand this by an example :
● If you want to find the record of roll 111 in the diagram, the first level index will look for the highest entry that is smaller than or equal to 111. At this amount, he'll get 100.
● Then again, it does max (111) <= 111 at the second index stage and gets 110. It now goes to the data block using the address 110, and starts looking for each record until it gets 111.
● This is how this approach is used to conduct a search. Often, adding, modifying or removing is performed the same way.
Key takeaway:
- Data can be stored in sorted order or may not be stored.
- The Primary Index is an ordered file with two fields and a fixed length scale.
- For this category, records which have similar characteristics are grouped and indexes are established in cluster index.
- In secondary indexing, another degree of indexing is added to reduce the mapping scale.
A self-balancing search tree is a B-Tree. It is presumed that everything is in the primary memory of most other self-balancing search trees (such as AVL and Red-Black Trees). We have to think of the vast amount of data that can not fit into the main memory to understand the use of B-Trees. When the number of keys is high, data in the form of blocks is read from the disc. Compared to the principal memory access time, disc access time is very high.
The key idea of using B-Trees is to decrease the amount of access to the disc. Most tree operations (search, insert, delete, max, min, ..etc) include access to the O(h) disc where the height of the tree is h. The B-tree is a tree with fat.
By placing the maximum possible keys into a B-Tree node, the height of the B-Trees is kept low. The B-Tree node size is usually held equal to the size of the disc block. Since the B-tree height is poor, total disc access is drastically reduced compared to balanced binary search trees such as AVL Tree, Red-Black Tree, etc. for most operations.
Time Complexity of B - tree
S.no. | Algorithm | Time complexity |
1 | Search | O ( log n) |
2 | Insert | O ( log n) |
3 | Delete | O ( log n) |
n is the total no. Of elements
All the properties of an M-way tree are found in the B tree of order m. Furthermore, it includes the properties below.
● In a B-Tree, each node contains a maximum of m children.
● With the exception of the root node and the leaf node, each node in the B-Tree contains at least m/2 kids.
● There must be at least 2 nodes for the root nodes.
● It is important to have all leaf nodes at the same level.
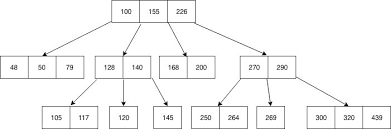
Fig 6: example of B - tree
The minimum height of the B-Tree that can exist with n node numbers and m is the maximum number that a node can have of children is:
hmin = [logm (n+1)] - 1
The maximum height of the B-Tree that can exist with n node numbers and d is the minimum number of children that can have a non-root node:
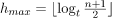
And 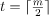
Traversal in B - tree
Traversal is also similar to Binary Tree's Inorder Traversal. We start with the leftmost child, print the leftmost child recursively, then repeat the same method for the remaining children and keys. In the end, print the rightmost child recursively.
Search operation in B - tree
A search in the Binary Search Tree is equivalent to a search. Let the search key be k. We begin from the root and traverse down recursively. For any non-leaf node visited, we simply return the node if the node has the key. Otherwise, we return to the appropriate child of the node (the child who is just before the first big key). If a leaf node is reached, and k is not contained in the leaf node, then NULL is returned.
Example: Searching 120 in the given B-Tree.
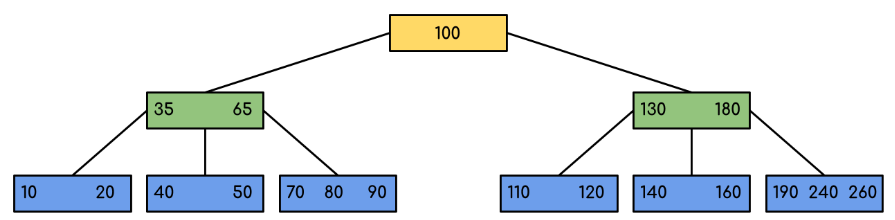
Fig 7: example for searching operation
Solution :
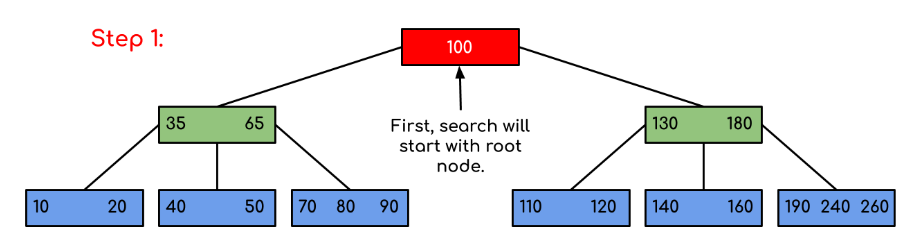
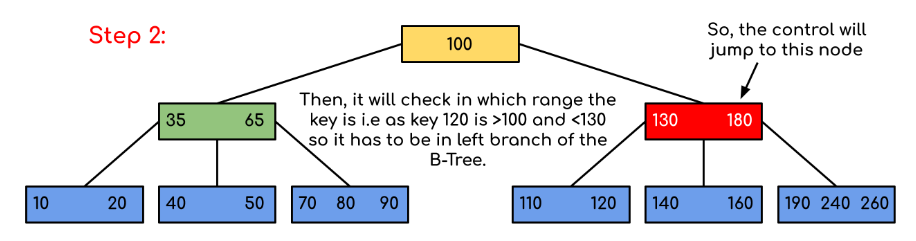
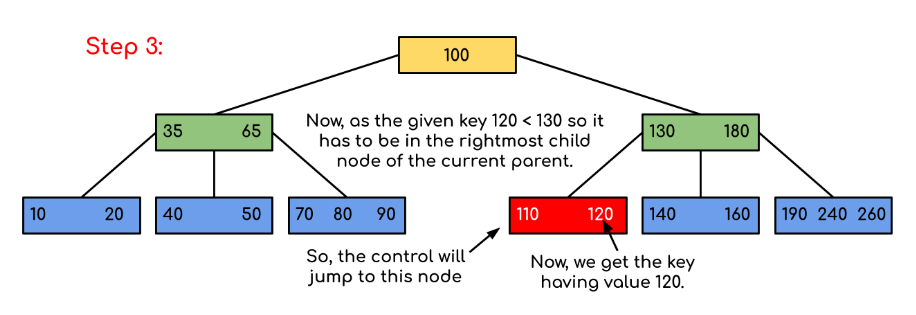
Fig 8: steps of searching
Key takeaway:
- A self-balancing search tree is a B-Tree.
- The key idea of using B-Trees is to decrease the amount of access to the disc.
- The B-Tree node size is usually held equal to the size of the disc block.
It is very inefficient to check for all the index values and reach the desired data in a large database structure. To determine the exact position of a data record on the disc without using the index structure, the hashing technique is used.
In this technique, data is stored using the hashing function in the data blocks whose address is generated. The location of the memory where these records are stored is known as data buckets or blocks of data.
A hash function can select any of the column values for the address to be produced. The hash function uses the primary key most of the time to produce the data block's address.
For any complex mathematical function, a hash function is a simple mathematical function. We can also consider the primary key itself as the data block's address. That means that each row whose address is stored in the data block will be the same as the primary key.
Terminology
- Hash Index: The Hash Index is the address of a data block. It comes from the hash value prefix.
- Key: A Database Management System (DBMS) key is a field or field collection that enables relational database users to define the database table rows/records uniquely.
- Hash function: This mapping feature matches all the search key sets to the addresses where the real records are stored. It is an easy feature of mathematics.
- Bucket Overflow: Bucket overflow is the state when the hash result is loaded with buckets. For any static function, this is the fatal step.
- Double Hashing: Double hashing is a method of computer programming used in hash tables to fix the problems of a collision.
- Quadratic Probing: It lets you decide the new address for the bucket. By adding the consecutive output of the quadratic polynomial to the starting value given by the original computation, it allows you to add Interval between probes.
- Data Bucket: The memory location where the records are located in the hash format. It is also known as the Storage Unit.
- Linear Probing: It is a concept in which the next available block of data is used instead of overwriting the older data block to insert the new record.
Types of Hashing
Fig 9: types of hashing
- Static Hashing
In this type of hashing, the address of the resulting bucket of data will always be the same. Let's take an example; if we want to use the mod(5) hash function to produce the address for Product ID= 76, it always provides the result in the same bucket address as 3. The number of data buckets still stays the same or constant in memory.
Below are the four static hashing operations:
- Search a Record
When we need to check for a record, the same hash function allows us to retrieve the address of the bucket where the information is stored.
- Insert a Record
The hash function automatically produces the address bucket for the record, based on the hash key, when we need to insert a new record into the table.
- Delete a Record
If we want to remove a record from the table, the record that we want to delete using the hash function will be read or retrieved. And, after that, for that memory address, we need to delete the record.
- Update a Record
If we want to update the current record in the table, then we must first check for the record to be modified by using the hash function. The data record is automatically changed then.
Static hashing is further divided into
- Open hashing
In the Open hashing process, the next available data block is used to enter the new record instead of overwriting the older one. This method is also known as linear probing.
For example, A2 is a new record that you want to insert, for example. The hash function creates an address like 222. But a certain other value is already occupied by it. That is why the machine searches for the next 501 data bucket and assigns it to A2.
- Close hashing
In this method of hashing, the new bucket is selected for the same hash result when the data bucket is filled with data, and is connected to the previously filled bucket. This method is referred to as Overflow-Chaining.
2. Dynamic Hashing
This method of hashing is used to solve the fundamental problem of static hashing. The problem with the static hashing technique is that it does not dynamically minimise or expand its size according to the size of the database.
In this type of hashing, as the records in the database increase or decrease, the data buckets are dynamically added or removed. This form of hashing is also known as prolonged hashing. To produce a large number of values, the hash function is generated.
Key takeaway:
- A hash function can select any of the column values for the address to be produced.
- The hash function uses the primary key most of the time to produce the data block's address.
- In Static hashing, the address of the resulting bucket of data will always be the same.
- To produce a large number of values, the hash function is generated.
References:
- “Database System Concepts”, 6th Edition by Abraham Silberschatz, Henry F. Korth, S. Sudarshan, McGraw-Hill
- “Principles of Database and Knowledge – Base Systems”, Vol 1 by J. D. Ullman, Computer Science Press
- “Fundamentals of Database Systems”, 5th Edition by R. Elmasri and S. Navathe, Pearson Education