Unit - 1
Introduction
Introduction
● The term "Automata" is derived from the Greek word "αὐτόματα" which means "self-acting". An automaton (Automata in plural) is an abstract self-propelled computing system that automatically follows a predetermined operation sequence.
● The primary reason behind the development of the automata theory was the development of methods to explain and analyze the complex behavior of separate systems.
Key takeaway:
- The automaton is called the abstract machine.
- It is the analysis of abstract machines and the problems of computation that can be solved by these machines.
Definition − An alphabet is any finite set of symbols.
Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.
Language
Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or
Infinite.
Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then
L = { ab, aa, ba, bb }
Grammar
Simplifying Context Free Grammars
A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production
Rules satisfy one of the following conditions:
A non-terminal generating a terminal (e.g.; X->x)
A non-terminal generating two non-terminals (e.g.; X->YZ)
Start symbol generating ε. (e.g.; S->ε)
Consider the following grammars,
G1 = {S->a, S->AZ, A->a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
Key takeaway:
- CNF is a pre-processing step used in various algorithms.
- For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.
A production, if its left side occurs on its right side, is called recursive. Production S→aS, for example, is recursive. A manufacturing A → α is recursive indirectly. If a sentence form that includes A is derived from A, then suppose we have the following grammar:
S → b/aA
A → c/bS
Due to the following derivations, the S → aA and A→ bs productions are both indirectly recursive:
S ⇒ aA ⇒ abS,
A ⇒ bS ⇒ baA
A grammar is recursive if either a recursive or indirectly recursive production is included in it.
Derivation
Derivation is a sequence of the laws of development. Via these production laws, it is used to get the input string. We have to take two decisions during parsing. That are like the following:
● The non-terminal that is to be replaced must be determined by us.
● We have to determine the law of development by which the non-terminal would be substituted.
We have two options to assess which non-terminal with the production rule is to be put.
- Left most derivation
The input is scanned and replaced with the development rule from left to right in the left-most derivation. So, we read the input string from left to right in the left-most derivation.
2. Right most derivation
The input is scanned and replaced with the production rule from right to left in the right-most derivation. So, we read the input string from right to left in the right - most derivation.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:
- Type 0 known as Unrestricted Grammar.
- Type 1 known as Context Sensitive Grammar.
- Type 2 known as Context Free Grammar.
- Type 3 Regular Grammar.
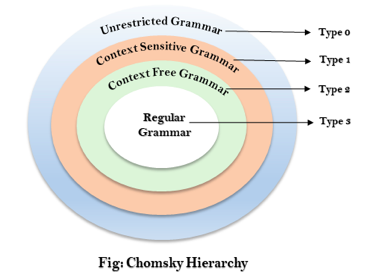
Fig 1: Chomsky hierarchy
The above diagram shows the hierarchy of Chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar. The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example:
- BAa → aa
- P → p
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar. Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway:
- Where the number of symbols in V is equal to or less than T
Example:
- S → AT
- T → xy
- A → a
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is :
A → α
Key takeaway:
- Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example:
- A → aBb
- A → b
- B → a
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar.Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modelled.
Type3 has to be in the form of -
V → T*V / T*
Example:
A → xy
Key takeaway:
- The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows −
● ε is a Regular Expression indicates the language containing an empty
String. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular
● Expression denoting the language L(Y), then
❏ X + Y is a Regular Expression corresponding to the language L(X) ∪
L(Y) where L(X+Y) = L(X) ∪ L(Y).
❏ X . Y is a Regular Expression corresponding to the language L(X) .
L(Y) where L(X.Y) = L(X) . L(Y)
❏ R* is a Regular Expression corresponding to the language L(R*)
Where L(R*) = (L(R))*
● If we apply any of the rules several times from 1 to 5, they are Regular
Expressions.
Unix Operator Extensions
Regular expressions are used frequently in Unix:
● In the command line
● Within text editors
● In the context of pattern matching programs such as grep and egrep
Additional operators are recognized by Unix. These operators are used for
Convenience only.
● character classes: ‘[‘<list of chars> ‘]’
● start of a line: ‘^’
● end of a line: ‘$’
● wildcard matching any character except newline: ‘.’
● optional instance: R? = epsilon | R
● one or more instances: R+ == RR*
Key takeaway:
- Regular languages are referred to as the languages recognised by certain regular expressions.
- A regular expression may also be defined as a pattern sequence that defines a series.
In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.
An automaton can be represented by a 5-tuple (Q, ∑, δ, q 0 , F), where −
● Q is a finite set of states.
● ∑ is a finite set of symbols, called the alphabet of the automaton.
● δ is the transition function.
● q 0 is the initial state from where any input is processed (q 0 ∈ Q).
● F is a set of final state/states of Q (F ⊆ Q).
Transition function can be defined as:
δ: Q x ∑→Q
Equivalence with regular expression
Successively replacing states and transitions in the DFA graph with transitions labelled with the corresponding regular expressions is one approach to transforming a DFA into an equivalent RE.
Note that any transformation in the DFA is initially de facto labelled with a periodic expression. A new final state should be formed with an ε-transition from each of the previous final states if there are several final states.
Consider the following FA, for instance, with three states.

A transformation labelled with the regular expression ab representing the concatenation of a and b can be substituted for state q1.

Next, with two states and two parallel transitions, consider the following FA.
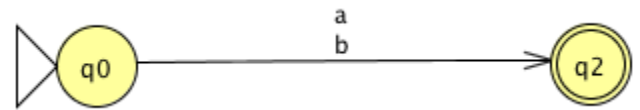
A single transition labelled with the regular expression a+b representing the union of a and b will replace the two transitions.
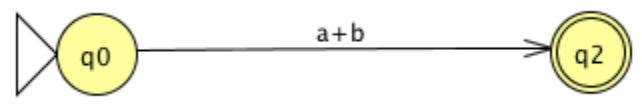
Now, consider the following FA, which involves a move to and from the same state.
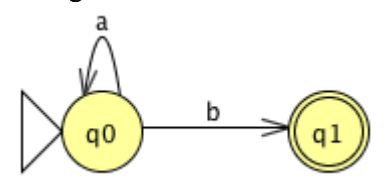
The Kleene star over a, which can be defined by the standard expression a*, indicates the transition. The two transitions can therefore be replaced by a single transition labelled with the standard expression a*b indicating that a* is concatenated with b.
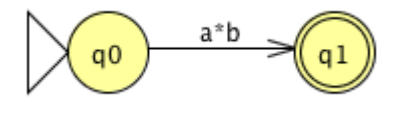
The mark on that transition is the regular expression equivalent to the original DFA once the FA graph has been decreased to two states (an initial state and a final state) and a single transition.
Key takeaway:
- it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton
- Any transformation in the DFA is initially de facto labelled with a periodic expression.
In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton. As it has a finite number of states, the machine is called Non- deterministic Finite Machine or Non- deterministic Finite Automaton.
It has a finite number of states.
Q → Finite non-empty set of states.
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State
Transition function can be defined as:
δ: Q x ∑ →2Q
Equivalence of DFA and NFA
It would seem superficially that deterministic and non-deterministic finite state automata are totally distinct beasts. However, it turns out that they are equivalent. There is a DFA for every language recognized by an NFA that recognizes that language and vice versa.
The NFA to DFA conversion algorithm is relatively simple, even though the resulting DFA is substantially more complicated than the original NFA. I will illustrate this equivalence after the hop and also go through a brief example of converting an NFA to an equivalent DFA.
DFA and NFA Theorem proof -
Let's formally state the theorem we are proving before continuing:
Theorem:
Let the language L ⊆ Σ* be recognized by NFA N = (Σ, Q, q0, F, δ) and assume L.
A DFA D= (Σ, Q ', q'0, F', δ ') exists that also accepts L. (L(N)= L(D)).
We are able to prove by induction that D is equal to N by allowing each state in the DFA D to represent a set of states in the NFA N. Let's define the parameters of D: before we start proofing,
● Q’ is equal to the powerset of Q, Q’ = 2Q
● q’0 = {q0}
● F’ is the set of states in Q’ that contain any element of F, F’ = {q ∈ Q’|q ∩ F ≠ Ø}
● δ’ is the transition function for D. δ’(q ,a ) = Up∈ q δ(p , a)for q ∈ Q’ and a ∈ Σ
It's worth more explaining, I think δ '. Note that in the set of states Q 'in D, each state is a set of states from Q in N itself. Determine the transition δ (p,a) for each state p in state q in Q 'of D (p is a single state from Q). The union of all δ (q, a) is δ(q,a) .
Now we will demonstrate δ’(q0’ , x) =δ’(q0 , x) that for every x i.e L(D) = L (N)
Key takeaway:
- In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine.
- the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton.
Regular expressions and finite automata have equivalent expressive power:
● For every regular expression R, there is a corresponding FA that accepts the
Set of strings generated by R.
● For every FA, A there is a corresponding regular expression that generates the set of strings accepted by A.
The proof is in two parts:
1. An algorithm that, given a regular expression R, produces an FA A such that
L(A) == L(R).
2. An algorithm that, given an FA A, produces a regular expression R such that
L(R) == L(A).
Our construction of FA from regular expressions will allow “epsilon transitions” (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols. We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular
Expression.
● If the operand is a character c, then our FA has two states, s0 (the start state)
And sF (the final, accepting state), and a transition from s0 to sF with label c.
● If the operand is epsilon, then our FA has two states, s0 (the start state) and
SF (the final, accepting state), and an epsilon transition from s0 to sF.
● If the operand is null, then our FA has two states, s0 (the start state) and sF
(the final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and
R1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1)
And B (with start state b0 and final state bF) be the machine accepting L(R2).
● The machine C accepting L(R1R2) includes A and B, with start state a0, final
State bF, and an epsilon transition from aF to b0.
● The machine C accepting L(R1|R2) includes A and B, with a new start state
c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and
From aF and bF to cF.
● The machine C accepting L(R1*) includes A, with a new start state c0, a new
Final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0,
And from aF to cF.
Eliminating Epsilon Transitions
If epsilon transitions can be eliminated from an FA, then construction of an FA
From a regular expression can be completed.
Epsilon transitions offers a choice: It allows us to stay in a state or move to a
New state, regardless of the input symbol.
If starting in state s1, state s2 can be reached via a series of epsilon
Transitions followed by a transition on input symbol x, replacement of the epsilon
Transitions with a single transition from s1 to s2 on symbol x.
Algorithm for Eliminating Epsilon Transitions
A finite automaton F2 can be built with no epsilon transitions from a finite
Automaton F1 as follows:
1. The states of F2 are all the states of F1 that have an entering transition
Labeled by some symbol other than epsilon, plus the start state of F1, which is
Also the start state of F2.
2. For each state in F1, determine which other states are reachable via epsilon
Transitions only. If a state of F1 can reach a final state in F1 via epsilon
Transitions, then the corresponding state is a final state in F2.
For each pair of states i and j in F2, there is a transition from state i to state j on input
x if there exists a state k that is reachable from state i via epsilon transitions in F1,
And there is a transition in F1 from state k to state j on input x.
Key takeaway:
- For every regular expression, there is a corresponding FA that accepts the
Set of strings generated by RE.
- The computer can switch to any combination of states in the NDFA.
- Epsilon closure for a given state X is a set of states that can only be reached with (null) or ε moves from states X, including state X itself.
- When the computer is given a single input to a single state, it goes to a single state in DFA.
Regular languages are closed under a wide variety of operations.
- Union and intersection
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection.
- Set complement
Pick a DFA recognizing the language, then swap the accept/non- accept markings on its states.
- String reversal
Pick an NFA recognizing the language. Create a new final state, with epsilon transitions to it from all the old final states. Then swap the final and start states and reverse all the transition arrows.
- Set difference
Rewrite set difference using a combination of intersection and set complement.
- Concatenation and Star
Pick an NFA recognizing the language and modify.
- Homomorphism
A homomorphism is a function from strings to strings. What makes it a homomorphism is that its output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w : w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For
Example, 0 * 1 * is regular, but its subset {O n 1 n : n >= 0} is not regular, but its subset {01, 0011, 000111} is regular again.
Theorem -
Let L be a regular language. Then a constant c' exists such that for every string w in L
|w| ≥ c
We are able to split w into three strings, w=xyz, so that
● |y| > 0
● |xy| ≤ c
● For all k ≥ 0, the string xyKz is also in L
Application of Pumping Lemma
It is important to apply Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.
● If L is regular, it satisfies Pumping Lemma.
● If L does not satisfy Pumping Lemma, it is non-regular.
Method for demonstrating that a language L is not regular
● We have to assume that L is regular.
● The pumping lemma should hold for L.
● Use the pumping lemma to obtain a contradiction −
● Select w such that |w| ≥ c
● Select y such that |y| ≥ 1
● Select x such that |xy| ≤ c
● Assign the remaining string to z.
● Select k such that the resulting string is not in L.
Therefore, L is not regular.
Example:
Prove that L = {aibi | i ≥ 0} is not regular.
Sol:
● At first, we assume that L is regular and n is the number of states.
● Let w = anbn. Thus |w| = 2n ≥ n.
● By pumping lemma, let w = xyz, where |xy| ≤ n.
● Let x = ap , y = aq , and z = arbn , where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
● Let k = 2. Then xy2z = apa2qarbn.
● Number of as = (p + 2q + r) = (p + q + r) + q = n + q
● Hence, xy2z = an+q bn . Since q ≠ 0, xy2z is not of the form anbn .
● Thus, xy2z is not in L.
Hence L is not regular.
It is possible to create infinitely many finite state automata for a given regular language L to accept L. The answer is that there will be a loop in the transition diagram centered on a given DFA M1 . To have more states and L(M1) = L(M2) = L, we can create a new DFA M2. And we can create a DFA M3 with even more states and L(M3) = L from DFA M2.
For instance, given a DFA M1, we can create a DFA M2 to have more states and
L(M1) = L(M2) = L.
Example: The following two DFA's are identical to M1 and M2. The collection above the alphabet Σ = {0,1} is accepted by {0n | n>0} both machines.

Fig 2: DFA diagram
Machine M2 states q1 , q2 and q3 are identical, we can combine these three states in one state as qt in machine M1.
The state qg and qh of the M2 machine are identical, these two states can be combined in one state as qf in the M1 machine.
References:
- Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of
Computation, Pearson Education Asia.
2. Dexter C. Kozen, Automata and Computability, Undergraduate Texts in Computer Science, Springer.
3. Michael Sipser, Introduction to the Theory of Computation, PWS Publishing.