Unit - 3
Straight bevel gear
Bevel Gears
Bevel gears are used to transmit power between two intersecting shafts. There are two common types of bevel gears are
- Straight Bevel Gear
- Spiral Bevel Gear
(i) Straight Bevel Gear The elements of the teeth of the straight bevel gears are straight lines, which converge into a common apex point shown in figure 1 (a).
(ii) Spiral Bevel Gear The elements of the teeth of the spiral bevel gears are spiral curves which also converge into a common apex point.

Figure: Types of Bevel Gears: (a) Straight Bevel Gear (b) Spiral Bevel Gear
Terminology
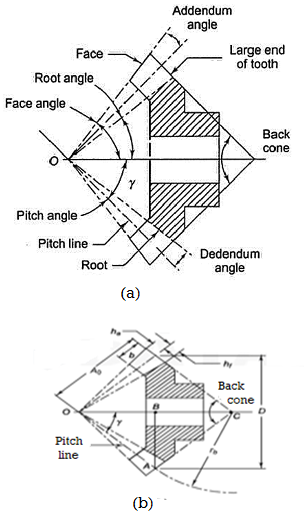
Figure. Terminology of Bevel Gear
A bevel gear is in the form of the frustum of a cone. The following terms are important in terminology of bevel gears:
(i) Pitch Cone Pitch cone is an imaginary cone, the surface of which contains the pitch lines of all teeth in the bevel gear.
(ii) Cone Centre The apex of the pitch cone is called the cone centre. It is denoted by O.
(iii) Cone Distance Cone distance is the length of the pitch-cone element. It is also called pitch-cone radius. It is denoted by A0 and it is given by

(iv) Pitch Angle The angle that the pitch line makes with the axis of the gear, is called the pitch angle. It is denoted by g. The pitch angle is also called centre angle.
(v) Addendum Angle It is the angle subtended by the addendum at the cone centre. It is denoted by a.
(vi) Dedendum Angle It is the angle subtended by the dedendum at the cone centre. It is denoted by d.
(vii) Face Angle It is the angle subtended by the face of the tooth at the cone centre.
Face angle = pitch angle + addendum angle = g + a
(viii) Root Angle It is the angle subtended by the root of the tooth at the cone centre.
Root angle = pitch angle – dedendum angle = g – d
(ix) Back Cone The back cone is an imaginary cone and its elements are perpendicular to the
Elements of the pitch cone.
(x) Back Cone Distance It is the length of the back cone element. It is also called back cone radius. It is denoted by rb.
Worm gear drives are used to transmit power between two non-intersecting shafts, which are, in general, at right angles to each other. The worm gear drive consists of a worm and a worm wheel.
The worm is a threaded screw, while the worm wheel is a toothed gear. The teeth on the worm wheel envelope the threads on the worm and give line contact between mating parts.
Worm and worm gear terminology
A pair of worm gears is specified and designated as z1/z2/q/m:
Where,
z1 = number of starts on the worm
z2 = number of teeth on the worm wheel
q = diametral quotient
m = module (mm)
The diametral quotient is given by,

Where,
d1=pitch circle diameter of the worm
(i) Axial Pitch (px) The axial pitch of the worm is defined as the distance measured from a point on one thread to the corresponding point on the adjacent thread, measured along the axis of the worm.
(ii) Lead The lead (l) of the worm is defined as the distance that a point on the helical profile will move when the worm is rotated through one revolution.
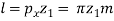
(iii) Lead Angle (γ) The lead angle is defined as the angle between a tangent to the thread at the pitch diameter and a plane normal to the worm axis.
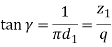
(iv) Helix Angle (ψ) The helix angle is defined as the angle between a tangent to the thread at the pitch diameter and the axis of the worm. The worm helix angle is the complement of the worm lead angle.
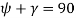
(v) Pressure Angle (α) The tooth pressure angle is measured in a plane containing the axis of the worm and it is equal to one-half of the thread angle.
Key Takeaways:
- The worm gear drive consists of a worm and a worm wheel.
- The lead angle is defined as the angle between a tangent to the thread at the pitch diameter and a plane normal to the worm axis.
- The worm helix angle is the complement of the worm lead angle.
The efficiency of a worm gear drive is low and then work done by friction is converted into heat. When the worm gears operate continuously, considerable amount of heat is generated. The rate of heat generated (Hg ) is given by,

Where,
Hg = rate of heat generation (W)
η = efficiency of worm gears (fraction)
KW = power transmitted by gears (kW)
The heat is dissipated through the lubricating oil to the housing wall and finally to the surrounding air. The rate of heat dissipated (Hd) by the housing walls to the surrounding air is given by,
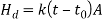
Where,
Hd = the rate of heat dissipation (W)
k = overall heat transfer coefficient of housing walls (W/m2 °C)
t = temperature of the lubricating oil (°C)
t0 = temperature of the surrounding air (°C)
A = effective surface area of housing (m2)
Equating the heat generated and heat dissipated we get,

From the above equation we can find the resultant temperature and the power transmitting capacity of worm gear drive.
The selection of materials for the worm and the worm wheel is more limited than it is for other types of gears.
The threads of the worm are subjected to fluctuating stresses and the number of stress cycles is fairly large. Therefore, the surface endurance strength is an important criterion in the selection of the worm material.
The core of the worm should be kept ductile and tough to ensure maximum energy absorption.
The following varieties of steel are used for the worm:
Normalized carbon steels—40C8, 55C8
Case-hardened carbon steels—10C4, 14C6
Case-hardened alloy steels–16Ni80Cr60, 20Ni2Mo25
Nickel–chromium steels—13Ni3Cr80, 15Ni4Cr1
The worm wheel cannot be accurately generated in the hobbing process. The final profile and finish of the worm wheel teeth is the result of plastic deformation during the initial stages of service. Therefore, the worm wheel material should be soft and conformable. Phosphor-bronze, with a surface hardness of 90–120 BHN, is widely used for the worm wheel.
The efficiency of the worm gear drive is given by,
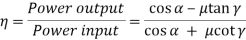
For self-locking drive,
μ > tan γ
For overrunning/reversible/back-driving drive
μ < tan γ
Example. 1 kW power at 720 rpm is supplied to the worm shaft. The number of starts for threads of the worm is four with a 50 mm pitch–circle diameter. The worm wheel has 30 teeth with 5 mm module. The normal pressure angle is 20°. Calculate the efficiency of the worm gear drive and power lost in friction.
Solution. Given kW = 1, N = 720, rpm α = 20°, d1 = 50 mm, Z1 = 4, Z2 = 30 teeth, m = 5 mm.
Efficiency of worm gear drive
Using
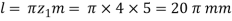

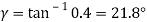

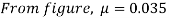
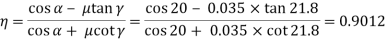
Power lost in friction

References:
1. Shigley J., Mischke C., Budynas R. And Nisbett K., Mechanical Engineering Design, 8thed., Tata McGraw Hill,2010.
2. Jindal U.C., Machine Design: Design of Transmission System, Dorling Kindersley,2010.
3. Maitra G. And Prasad L., Handbook of Mechanical Design, 2nd ed., Tata McGraw Hill,2001.