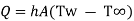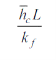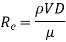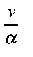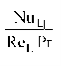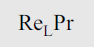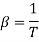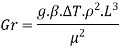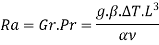Unit 2
Heat convection
The process of heat transfer between a solid surface and fluid in motion is called convection.
2.1.1 Types of fluid
2.1.2. Laminar and turbulent flow
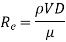
Where  =density,
=density,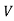 =velocity,D=diameter of pipe,
=velocity,D=diameter of pipe,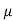 =viscosity
=viscosity
2.1.3. Newton’s law of cooling
Rate of convective heat transfer is determined by Newton’s law of cooling.
It states that rate of heat transfer is proportional surface area perpendicular to heat flow direction and temperature difference between wall surface (Tw) and fluid temperature (T∞) in direction perpendicular to flow.
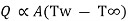
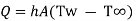 ...(2.1)
...(2.1)
Where, Q is rate of heat transfer (W), A is area in m2, h is constant known as coefficient of convective heat transfer or film coefficient with unit W/m2K.
External flow convection-Convection takes place as fluid flows over body with temperature difference.
Internal flow convection- Convection takes place as fluid flows inside body with temperature difference.
Natural convection- The convection in which fluid moves due to density difference caused by heat transfer between solid surface and fluid it said to be natural or free convection.
Forced convection-If fluid motion is imparted by external means like pump is called forced convection.
2.4.1. Velocity boundary layer
When a fluid flows over a flat plate and its velocity is measured at various points normal to the surface in the immediate vicinity of the wall, a velocity profile is obtained.
The velocity begins with the value zero at the wall and increases within a thin layer of thickness d to the value of free-stream velocity u∞. This distance from the wall  is called the boundary layer thickness where there is velocity gradient and above which velocity is uniform and there is no viscous effect.
is called the boundary layer thickness where there is velocity gradient and above which velocity is uniform and there is no viscous effect.
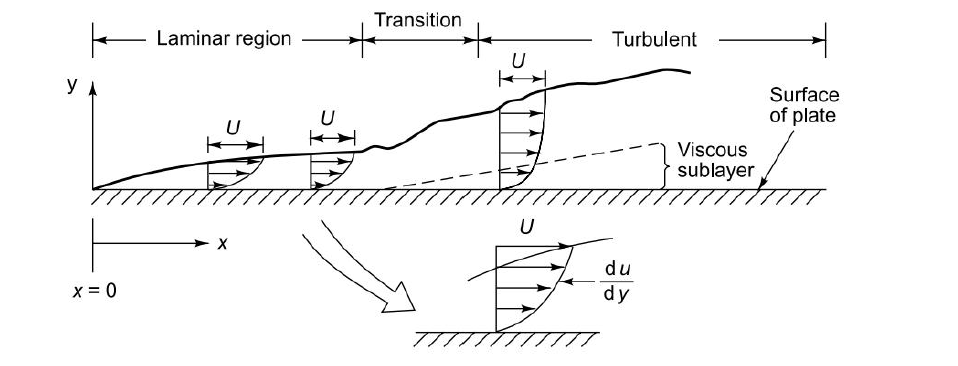
Fig 2.1 Velocity profiles in laminar, transition and turbulent boundary layers in flow over a flat plate
The fluid is moving in the laminar regime, and the boundary layer is thin. This is called laminar boundary layer. As the fluid travels further downstream along the plate, the retardation of fluid flow progresses due to viscous shear, and the boundary layer grows in thickness. As a result the velocity gradient gradually decreases. Meanwhile the boundary shear is reduced as the thick ness increases. When the boundary layer becomes thick enough, the particles begin to move out of the smooth layers, the laminar motion becomes unstable, and finally the flow becomes turbulent.
Thickness of velocity boundary layer is defined as distance from surface at which local velocity is 99% of free stream velocity.
2.4.1 Thermal boundary layer
Analogous to the concept of velocity boundary layer, one can visualize the development of a thermal boundary layer with temperature varying from Tw to 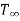 in the boundary layer thickness
in the boundary layer thickness 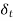 . Let us consider that a fluid at a uniform temperature
. Let us consider that a fluid at a uniform temperature 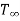 flows along a flat plate maintained at a constant temperature Tw. If we define the dimensionless temperature
flows along a flat plate maintained at a constant temperature Tw. If we define the dimensionless temperature 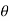 (x, y) as
(x, y) as
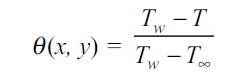
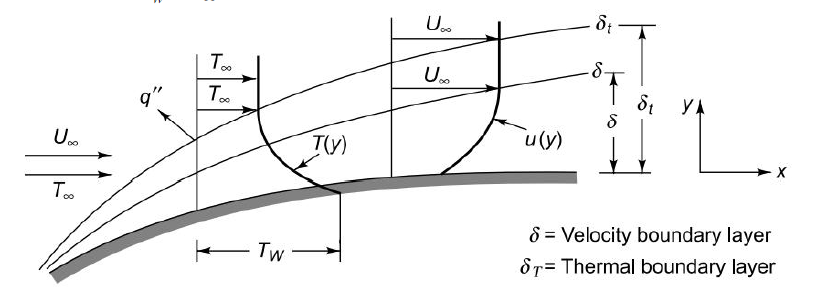
Fig 2.2 Growth of velocity and thermal boundary layers in flow over a flat surface
where T (x, y) is the local temperature in the fluid, then at y = 0,  = 0 and at y =
= 0 and at y =  ,
,  = 1. Therefore, at each location x along the plate one finds a location y =
= 1. Therefore, at each location x along the plate one finds a location y = 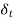 (x) in the fluid where q equals 0.99. The locus of such points where
(x) in the fluid where q equals 0.99. The locus of such points where  = 0.99 is called the thermal boundary layer
= 0.99 is called the thermal boundary layer 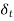 (x).
(x).
The relative thickness of the thermal boundary layer 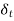 (x) and the velocity boundary layer
(x) and the velocity boundary layer 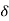 (x) depend on the Prandtl number of the fluid.
(x) depend on the Prandtl number of the fluid.
2.4.2 Velocity boundary layer in circular pipes
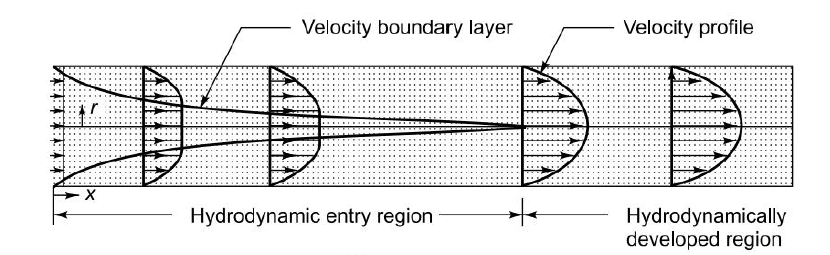
Fig 2.3 Velocity profile in circular pipe
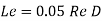
Where Re= Reynold’s number, D= diameter
For turbulent flow
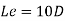
2.4.3 Thermal boundary layer in circular pipes

Where Re= Reynold’s number, D= diameter, Pr= Prandtl number
For turbulent flow
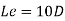

Fig 2.4 Development of thermal boundary layer in a tube (a) when T > Tw and (b) when Tw > T
There are various methods available for finding out heat transfer coefficient as there are many terms involved as compared to heat conduction. These methods are:
This method is simple and used widely. Biggest limitation of this method is that it is incomplete and highly dependent on experimental data. Understanding the concept is difficult by the use of dimensional method. It relates dimensionless number with experimental data with the help of correlations.
This method depends on fluid motion and transfer energy in form of simultaneous equations. This method helps in better understanding of physics behind the concept mathematically. Exact solutions are, however, important because the assumptions made can be specified precisely and their validity can be verified experimentally. High speed computers have made it easy to use this method nowadays.
It avoids use of complex mathematical equations and provides simple solution to equations used to describe thermal and velocity boundary layer. The problem is then analysed on a macroscopic basis by applying the equation of motion and the energy equation to the fluid in the boundary layer. This method is relatively simple and yields solutions within accuracy.
This method is useful for analyzing turbulent heat convection. One such model explains a mixing motion in a direction perpendicular to the mean flow accounting for the transfer of momentum as well as energy. Experimental results are agree with analytical predictions based on the model.
These methods are used to solve equations of motion and energy. These methods can be easily programmed in computer. Numerical methods can handle very complex equations.
The convection in which fluid moves due to motion imparted by external means like pump is called forced convection.
Convection heat transfer coefficient depends on large number of variables like density, dimension of pipe, viscosity etc. various methods are can be opted to find heat transfer. One of which is dimensionless analysis which deals with usage of characteristic dimensionless numbers.
2.6.1. Dimensionless numbers
Dimensionless heat transfer coefficient. It is ratio of convection heat transfer to conduction in a fluid layer of thickness L.
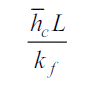
…(2.2)
It measure energy transfer by convection occurring at surface.
If Nu=1, heat transfer is purely by conduction. Larger the value of Nu, larger will be rate of heat transfer by convection.
Ratio of inertia to viscous forces.
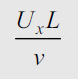
…(2.3)
L=characteristic length which is equal to diameter in pipes. U=velocity and
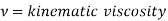
It characterizes type of flow, whether laminar or turbulent.
Ratio of molecular momentum diffusivity to thermal diffusivity.
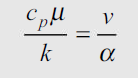
…(2.4)
Cp=specific heat, u=dynamic viscosity, 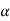 =thermal diffusivity.
=thermal diffusivity.
Higher the Pr higher is Nu and higher is the heat transfer.
It is dimensionless heat transfer coefficient. It is ratio of convective heat flux to heat transfer capacity.
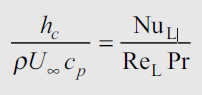
…(2.5)
NuL=Nusselt number, ReL=Reynolds number for liquid, 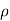 =density.
=density.
It is product of Reynolds and Prandtl numbers.

…(2.6)
2.6.2. Correlations for various shapes
Correlation between dimensionless numbers and convective heat transfer coefficient are used to determine heat flow rate.
2.6.2.1. Flow over the plate (External flow)
Local Nusselt number: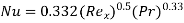
Average Nusselt number: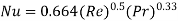
Local Nusselt number: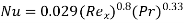
Average Nusselt number: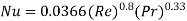
2.6.2.2. Flow through pipes (Internal flow)
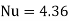 (for constant heat flux)
(for constant heat flux)
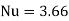 (for constant wall temperature)
(for constant wall temperature)
When fluid is heated i.e. 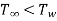 :
: 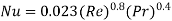
When fluid is cooled i.e.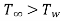 :
: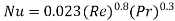
From value of Nusselt number, value of convective heat transfer coefficient can be found out which is then used to find heat transfer rate.
Mean film temperature=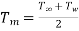
2.6.2.3. Characteristic length
Characteristic length also known as hydraulic diameter is important parameter for analysis of convection. As the geometry of conduit changes in internal flow, this length also changes. It is given as
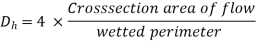
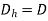
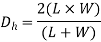
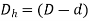
D=Outer diameter, d=inner diameter
2.6.3. Difference between average and local heat transfer coefficient
The convection in which fluid moves due to density difference caused by heat transfer between solid surface and fluid it said to be natural or free convection.
2.7.1. Mechanism of natural convection
2. 7.2. Coefficient of volumetric expansion
The coefficient of volumetric expansion is defined as density of fluid variation per degree change in temperature at constant pressure. It is denoted by 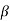 and equal to
and equal to
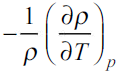
…(2.7)
Negative sign since density decrease with increase in temperature. For ideal gas
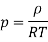
Therefore,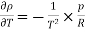
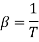
Higher value of  higher will be density gradient hence higher heat transfer rate.
higher will be density gradient hence higher heat transfer rate.
2.7.3. Dimensionless numbers
It represents the product of buoyant and inertia forces to the square of viscous force.

The role of Grashoff number in natural convection is similar to role of Reynolds number in forced convection. It provides criteria to decide whether flow is laminar or turbulent.
It is defined as product of Grashoff number and Prandtl number.
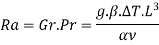
2.7.4. Correlations for various shapes
Nu=0.59(Gr.Pr)0.25 when 104<Gr.Pr<109
Nu=0.13(Gr.Pr)0.33 when 109<Gr.Pr<1012
Nu=0.54(Gr.Pr)0.25 when 105<Gr.Pr<2 x 107
Nu=0.15(Gr.Pr)0.33 when 2 x 107<Gr.Pr<3 x 1010
Sr. No. | Forced Convection | Natural convection |
1 | If movement of molecules occurs due to external force or by using external means like pumps is called forced convection. | If movement of molecules is due to density difference then such type of convection is natural convection. |
2 | Heat transfer rate is more. | Heat transfer rate is less. |
3 | External power is required for heat transfer. | No external power is required. |
4 | Dimensionless numbers used are Reynolds number, Nusselt number, Stanton number, Pecelt number. | Dimensionless numbers used are Grashoff number and Prandtl number. |
5 | Applications are in heat exchanger. | Application is cooling of tea in atmosphere. |
Another method of analysis of convection is approximate solution of momentum and energy equation. To determine the forced convection heat transfer coefficient hc and the friction coefficient Cf for incompressible steady laminar flow over a flat surface, we must satisfy the continuity, momentum and energy equations simultaneously.
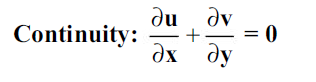
…(2.7)
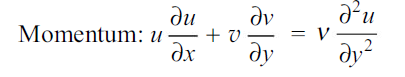
…(2.8)
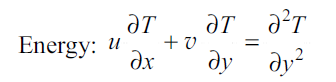
..(2.9)
Equation (2.8) must be solved simultaneously with the continuity equation, (Eq.2.7), in order to determine the velocity distribution, boundary layer thickness and skin friction coefficient. Let us first make an order-of-magnitude analysis of the differential equations to obtain the functional form of the solution. Within the boundary layer we may say that the velocity u is of the order of free-stream velocity 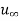 . Similarly, the y dimension is of the order of the boundary layer thickness
. Similarly, the y dimension is of the order of the boundary layer thickness 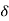 . Thus
. Thus
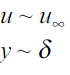
And continuity equation can be approximated as
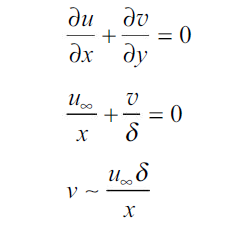
Then, by using this order of magnitude for 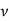 , the analysis of momentum equation would yield
, the analysis of momentum equation would yield
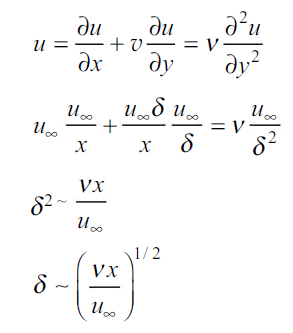
…(2.10)
Dividing by x to express the result in dimensionless form gives
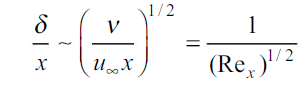
…(2.11)
This is the functional relationship of  with the local Reynolds number. Since the velocity profiles have similar shapes at various distances from the leading edge of the flat plate, the important variable is y/
with the local Reynolds number. Since the velocity profiles have similar shapes at various distances from the leading edge of the flat plate, the important variable is y/ , and we assume that the velocity may be expressed as a function of this variable.
, and we assume that the velocity may be expressed as a function of this variable.
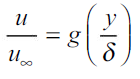
Introducing the order-of-magnitude estimate for 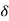 from 2.10
from 2.10
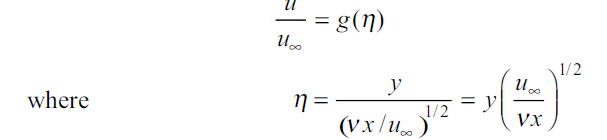
…(2.12)
Where
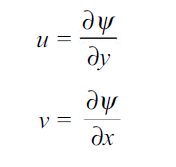
Here, 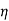 is called the similarity variable and
is called the similarity variable and  is the function for which we seek a solution. In accordance with the continuity equation, a stream function
is the function for which we seek a solution. In accordance with the continuity equation, a stream function 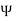 may be defined so that
may be defined so that
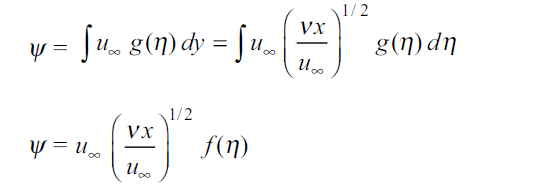
…(2.13)
From 2.13 and 2.12

…(2.14)
Where
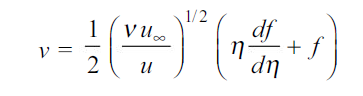
From 2.13 and 2.14
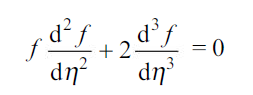
…(2.15)
Expressing 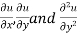 in terms of
in terms of  and inserting these relations in 2.8
and inserting these relations in 2.8

…(2.16)
It may be solved numerically for the function f(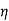 ) subject to the three boundary conditions:
) subject to the three boundary conditions:
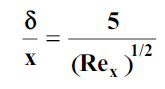
the solution to Eq. (2.16) was first obtained by Blasius
Figure 2.5 shows the Blasius velocity profiles in the laminar boundary layer on a flat plate in dimensionless form together with the experimental data. The ordinate is the ratio of local and free-stream velocities, and the abscissa is a dimensionless distance parameter (y/x) (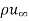 x/ m)1/2. The velocity u reaches 99% of the free-stream velocity
x/ m)1/2. The velocity u reaches 99% of the free-stream velocity 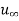 at (y/x) (
at (y/x) ( x/m)1/2 = 5.0. If we define the hydrodynamic boundary layer thickness d as that distance from the surface at which the local velocity u reaches 99% of the free-stream velocity
x/m)1/2 = 5.0. If we define the hydrodynamic boundary layer thickness d as that distance from the surface at which the local velocity u reaches 99% of the free-stream velocity 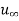 , then
, then
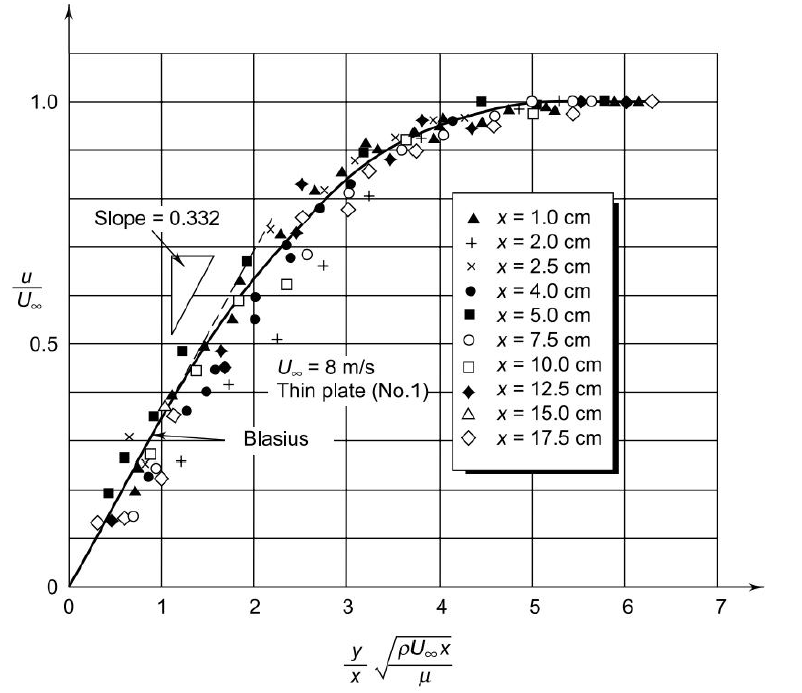
…(2.17)
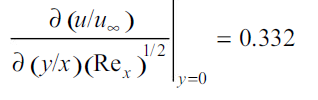
Fig 2.5 Velocity profile in a laminar boundary layer according to Blasius, with the experimental data
The shear stress at the wall can be obtained from the velocity gradient at y = 0 in Fig. 2.5. We find that
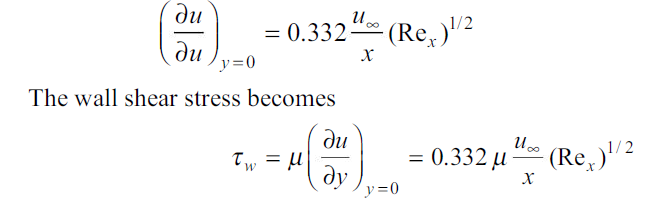
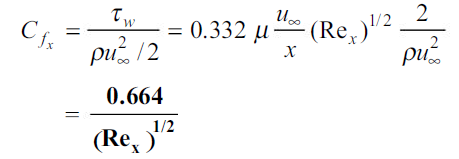
…(2.18)
It may be noted that the wall shear stress at the leading edge (x = 0) is very large, and it decreases with increasing distance (x) from the leading edge. Dividing both sides of Eq. (2.18) by the dynamic pressure of the free-stream, 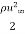 , we obtain
, we obtain
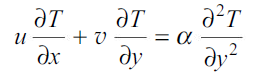
…(2.19)
where Cfx is the dimensionless local drag or friction coefficient.
Convective heat transfer coefficient:
The velocities u and v in the energy conservation equation

have the same values at any point (x, y) as in the momentum equation, Eq. (2.8). For the case of the flat plate, Pohlhausen used the velocities calculated previously by Blasius to obtain the solution for the heat transfer problem. If the momentum and energy equations are compared, we find them to be similar if 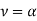 and the surface temperature Tw is constant. A solution for u (x, y) is also a solution for T (x, y) which can easily be checked if the symbol T is replaced by the symbol u while the boundary conditions for both are identical. If we define a dimensionless temperature
and the surface temperature Tw is constant. A solution for u (x, y) is also a solution for T (x, y) which can easily be checked if the symbol T is replaced by the symbol u while the boundary conditions for both are identical. If we define a dimensionless temperature
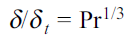
where Tw is the wall or surface temperature and 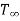 is the free–stream temperature. The condition
is the free–stream temperature. The condition 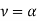 corresponds to a Prandtl number (=
corresponds to a Prandtl number (=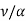 ) of unity. For Pr = 1, the velocity distribution is identical to the temperature distribution. The transfer of momentum is analogous to the transfer of heat when Pr = 1. For gases Prandtl number ranges from 0.6 to 1.0. The analogy is, therefore, satisfactory for gases. Liquids, however, have Prandtl numbers considerably different from unity, and the preceding analysis is not applicable directly to liquids.
) of unity. For Pr = 1, the velocity distribution is identical to the temperature distribution. The transfer of momentum is analogous to the transfer of heat when Pr = 1. For gases Prandtl number ranges from 0.6 to 1.0. The analogy is, therefore, satisfactory for gases. Liquids, however, have Prandtl numbers considerably different from unity, and the preceding analysis is not applicable directly to liquids.
We define a thermal boundary layer thickness d t as the distance from the wall at which the temperature difference between the wall and the fluid 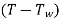 reaches 99% of the free-stream value
reaches 99% of the free-stream value 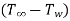 . From the temperature profi les, we observe that for Pr < 1,
. From the temperature profi les, we observe that for Pr < 1, 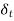 >
> 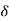 , and for fluids having Pr > 1,
, and for fluids having Pr > 1, 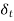 <
< 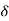 . According to Pohlhausen,
. According to Pohlhausen,
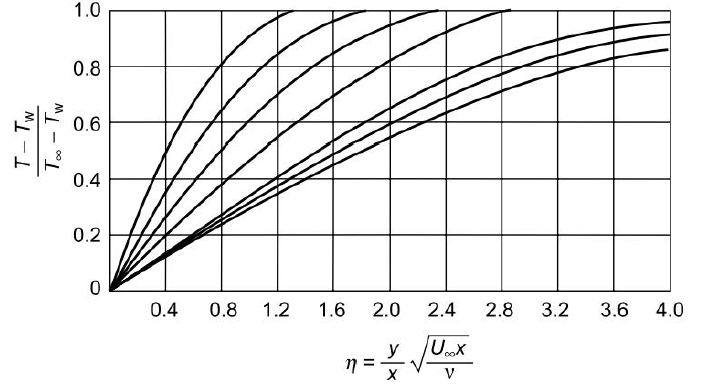

Fig2.6 Temperature distributions in a fluid flowing over a heated plate for various Prandtl numbers
The curves of Fig. 2.6 are replotted in Fig. 2.7 using the correction factor Pr1/3 in the abscissa, which is now (y/x) (Rex)1/2 Pr1/3. The dimensionless temperature gradient at the surface ( y = 0) is
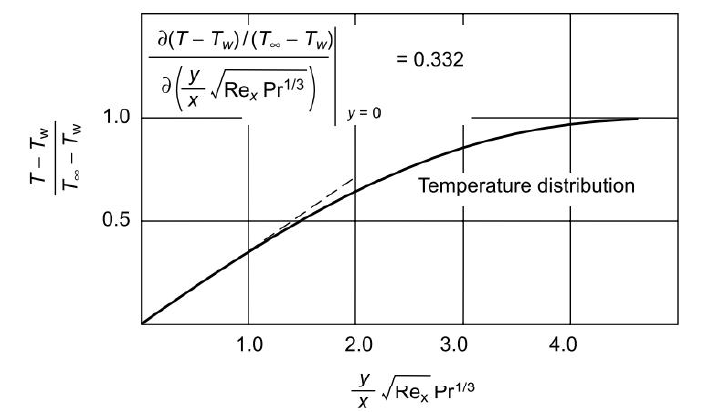
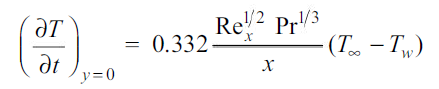
Fig 2.7 Temperature distribution for laminar flow over a heated plate at uniform temperature
Therefore, at any specified value of x,
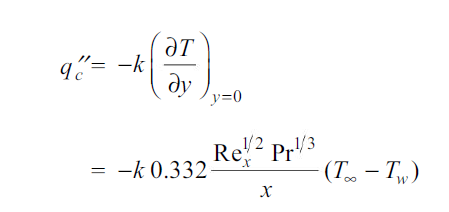
The local rate of convection heat transfer per unit area becomes

…(2.20)
The total rate of heat transfer from a plate of width b and length L is
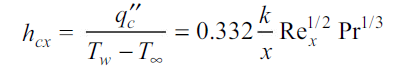
The local heat transfer coefficient obtained from Eq. (2.20),
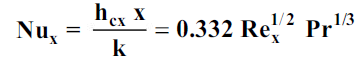
The local Nusselt number is
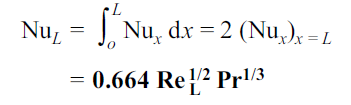
The average Nusselt number over the entire plate of length L is
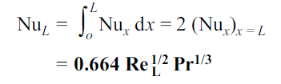
Average friction coefficient 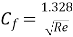
Local friction coefficient 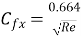
Thickness of boundary layer 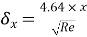
Thickness of thermal boundary layer 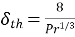
Average friction coefficient 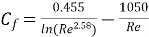
Local friction coefficient 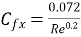
Thickness of boundary layer 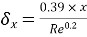
Heat transfer convection transfer |
|
Nusselt number |
|
Reynolds number |
|
Prandtl number |
|
Stanton number |
|
Peclet number |
|
Coefficient of volumetric expansion |
|
Grashoff number |
|
Rayleigh number |
|