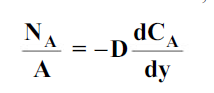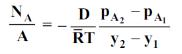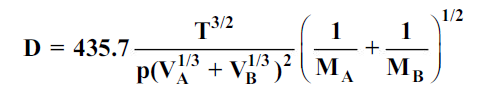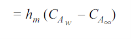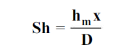Unit 6
Mass Transfer
2. Physical origins

Fig6.1 Mass transfer by diffusion
3. Fick’s Law
Mass transfer by molecular diffusion is analogous to heat transfer by conduction or momentum transfer in laminar flow. Mass transfer by molecular diffusion may occur in a stagnant fluid or in a fluid in laminar flow. Like the Fourier’s equation of heat conduction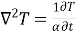 , the concentration field of the diffusing species A is given by
, the concentration field of the diffusing species A is given by

where CA is the concentration of component A in a mixture of A and B in kgmol/m3, t is the time in seconds and D is the mass diffusivity in m2/s.
For one-dimensional mass diffusion,
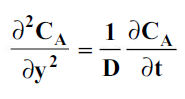
wherey is the distance in the direction of diffusion.
Like the conduction equation
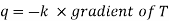
The mass transfer equation is
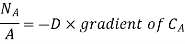
For one dimensional mass transfer
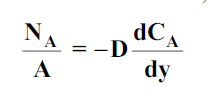
…(6.1)
where NA/A is the mass flux in kgmol/m2s. The negative sign appears because the concentration gradient is negative in the direction of mass transfer.
Equation (6.1) is called Fick’s law of diffusion, which states that the mass flux of a constituent per unit area is proportional to the concentration gradient.
In Fig. 6.2 a thin partition separates the two gases A and B. When the partition is removed, the two gases diffuse through each other until equilibrium is established and the concentration of the gases is uniform throughout the box. The diffusion rate is given by Eq. (6.1). It can also be expressed in terms of mass flow:
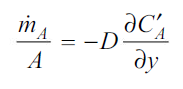
…(6.2)
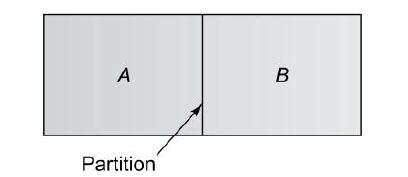
Fig6.2 Diffusion of component A into component B and vice versa
where is the mass flux per unit time, kg/s; CA is the mass concentration of component A per unit volume, kg/m3; and D is the proportionality constant called diffusion coefficient, m2/s.
is the mass flux per unit time, kg/s; CA is the mass concentration of component A per unit volume, kg/m3; and D is the proportionality constant called diffusion coefficient, m2/s.
4. Equimolar diffusion
In the gas phase, the concentrations are usually expressed in terms of partial pressures. If ideal gas law is assumed to hold good.
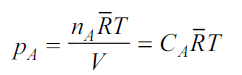
where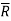 is the universal gas constant.
is the universal gas constant.
Fick’s law could then be written as
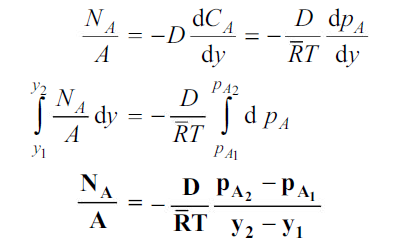
…(6.3)
wherepA1 is the partial pressure of A at y1 and pA2 is the partial pressure of A at y2.
Equation (6.3) is valid for equimolar counter diffusion in which gases A and B diffuse simultaneously in opposite directions through each other. The rates of diffusion are equal but in opposite direction i.e., NA = – NB.
And also
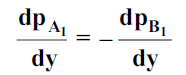
5. Molecular diffusion through stationary gas
Let us consider a gas Adiffusing through a stationary gas B into a liquid–vapour interface where the gas A is absorbed. Since the gas A is diffusing towards the interface, there must be a partial pressure gradient for A in the direction of diffusion.
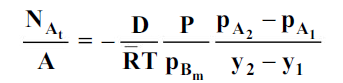
Where 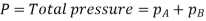 and
and 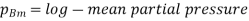 which is
which is
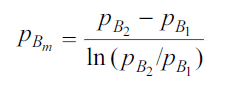
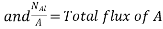
6. Diffusivity For Gases And Vapours
Gilliland proposed a semi-empirical equation for the diffusion coefficient in gases.
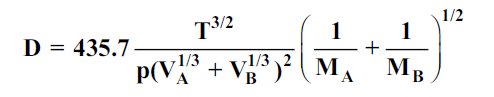
…(6.4)
whereD is in cm2/s, T is in K, p is the total system pressure in pascals and VAand VBare the molecular volumes of constituents A and B as calculated from the atomic volumes; MAand MBare the molecular weights of constituents A and B.
7. Concentration boundary layer and mass transfer coefficient
Just as the calculation of momentum and heat transfer requires the knowledge of velocity and temperature profiles within the boundary layer, the calculation of mass transfer requires that concentration profile within the boundary layer should be known.
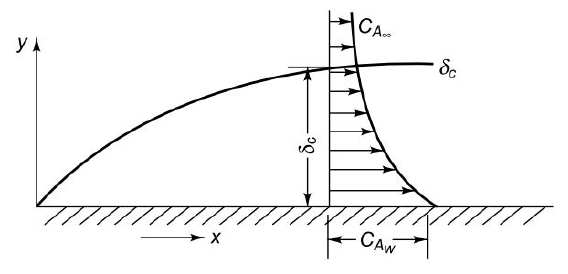
Fig6.3 Concentration boundary layer
Let us consider the flow of a fluid mixture on a surface as shown in figure. Let the free stream velocity and concentration be 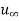 and
and 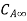 . Let the plate surface be maintained at a concentration
. Let the plate surface be maintained at a concentration  >
>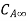 . Then, species A diffuses from the surface into the fluid. A concentration boundary layer develops , thickness of which can be defined in the same way as that of the hydrodynamic or thermal boundary layer. The distance
. Then, species A diffuses from the surface into the fluid. A concentration boundary layer develops , thickness of which can be defined in the same way as that of the hydrodynamic or thermal boundary layer. The distance  to which the boundary layer extends may be defined as the thickness at which the concentration is equal to 99% of the free-stream concentration
to which the boundary layer extends may be defined as the thickness at which the concentration is equal to 99% of the free-stream concentration
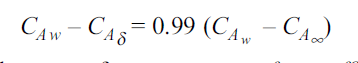
By analogy of heat transfer, mass transfer coefficient hm can be defined as
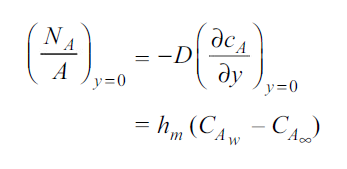
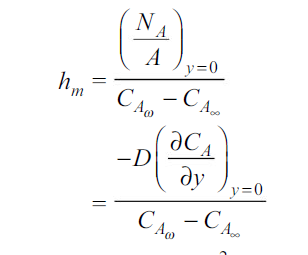
…(6.5)
Unit of hm is same as velocity i.e m/s.
The molecular diffusion equation is
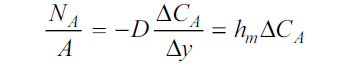
For gas

8. Analogy Between Momentum, Heat And Mass Transfer
The momentum and energy equations of a laminar boundary layer are
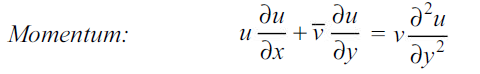

The concentration boundary layer can similarly be simplified to
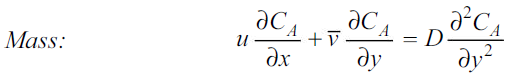
Momentum transfer in laminar flow (Newton’s law) is
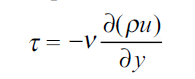

We know that the velocity and temperature profiles have the same shape if
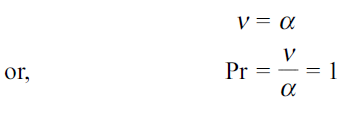
Similarly, the momentum and concentration profiles will have the same shape if
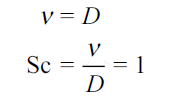
Where 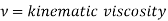
Thus, the Schmidt number plays the same role in mass transfer as does the Prandtl number in heat transfer.
It is also seen that the temperature and concentration profiles will be similar if
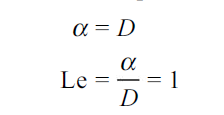
Where 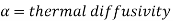
Thus, Lewis number is important in the solution of simultaneous heat and mass transfer problems. When,
Sc = Pr = Le = 1, all the three boundary layers coincide.
The dimensionless mass transfer number corresponding to the Nusselt number is the Sherwood number defined as
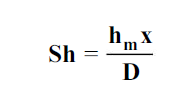
...(6.6)
wherex is the characteristic length.
Similarly, corresponding to Stanton number, which is expressed as
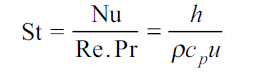
Corresponding to it, we have
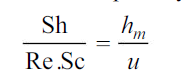
whereu is any characteristic velocity of the system.
We know that forced convection heat transfer correlations are of the form
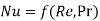
Likewise, in forced convection mass transfer problems we write the functional relation
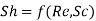
Heat transfer and Mass transfer are similar very similar to one another. Similarities between them can be explained by following key points.
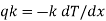
Where, qkis the rate of heat flux (a vector) in W/m2, dT/dx is the temperature gradient in the direction of heat flow x and k is the constant of proportionality
Mass transfer is explained with help of Fick’s law which is given as
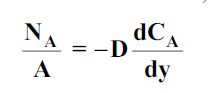
where NA/A is the mass flux, 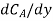 is concentration gradient and D is constant of proportionality.
is concentration gradient and D is constant of proportionality.
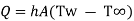
Where, Q is rate of heat transfer (W), A is area in m2, h is constant known as coefficient of convective heat transfer or film coefficient with unit W/m2K.
Mass convection equation is given as
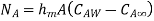
Where 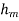 is coefficient of mass convection,
is coefficient of mass convection, 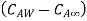 represent concentration difference.
represent concentration difference.
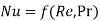
Likewise, Sherwood number, Reynold’s number and Schmidt number are governing constants in convection mass transfer which can be correlated as
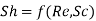
Important Formulae
Mass flux |
|
Equimolar diffusion |
|
Diffusivity of gas and vapour |
|
Mass flux by convection |
|
Sherwood’s number |
|
References