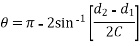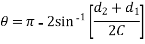Unit 3
Friction devices
Belt drives are the drives which are used to transmit power from one shaft to anothershaft. These are two types of belt drives flat (rectangular cross- section) and V (trapezoidal cross-section) belts.
Flat Belt Drive
The flat belt is mostly used, where a moderate amount of power is to be transmitted, from one pulley to another when the two pulleys are not more than 8 meters apart such as factories and workshops.
Velocity Ratio in Belt Drive
Velocity ration of a belt drive can be defined as the ratio of angular velocity of driven pully to the angular velocity of driving pully. Consider figure 1.
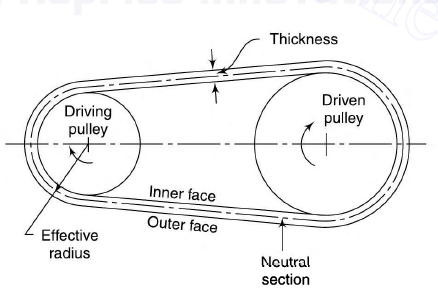
Figure 1 Flat belt drive
Let N1 = rpm of the driving pulley
N2 = rpm of the driven pulley
D1 = diameter of the driving pulley
D2 = diameter of the driving pulley
t = thickness of belt
Assumptions
(i) There is no relative motion between the belt and pulley.
(ii) Belt is inelastic.
Hence, speed of driving pully = speed of driven pulley
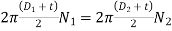
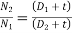
If we neglect the thickness of the belt we get,
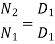
Slip
Slip in case of the belt drive can be defined as the difference between the velocity of belt and the pully on the driving and driven side. Slip is an undesirable phenomenon which causes reduction in speed of belt on driving shaft which results in decrease in speed of driven shaft.
Let, S1 = slip between the driver and the belt
S2 = percentage slip between the belt and the follower
S = total percentage slip.
Linear speed of belt on driver = 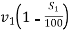
Linear speed of follower, 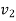 =
= 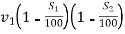
= 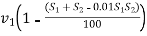
We know that  and
and 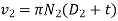
Substituting, 

Law of Belting
The law of belting states that the center line of the belt as it approaches the pulley must lie in a plane perpendicular to the axis of that pulley, or must lie in the plane of the pulley, otherwise the belt will run off the pulley.
 Length of Open Belt
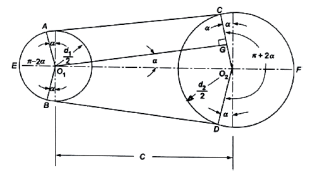
Length of Open Belt
Consider the belt drive shown in figure 2.
The length of open belt is given by
L0 = arc AEB + BD + arc DFC + AC
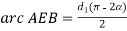
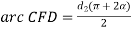 Figure .2. Open flat belt drive
Figure .2. Open flat belt drive
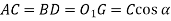
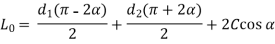
From Figure 2
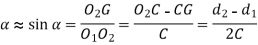
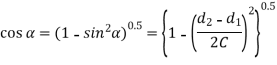
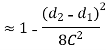
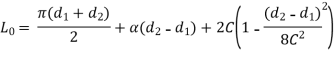
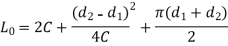
Length of Cross Belt
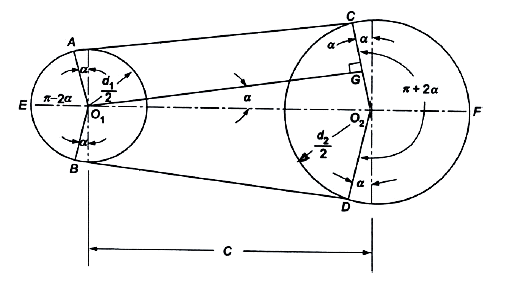
Figure.3. Cross flat belt drive
Consider the belt drive shown in figure 3.
The length of open belt is given by
L0 = arc AEB + BC + arc DFC + AD
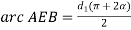
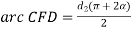
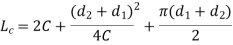
Derivation is similar to the length for open belt drive.
Angle of arc of contact
Belt type | Angle of arc of contact |
Open belt |
|
Cross belt |
|
Ratio of Belt Tension
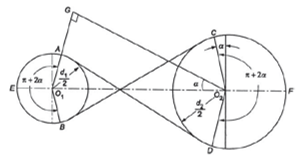
Let us consider Figure 4
T1= tension in Tight side.
T2= tension in slack side.
= angle of contact on the pulley.
Consider an element AB making angle at center, and change in tension in this portion be T to T +T from A to B. R and R be the normal reaction and force of friction.
Resolving the forces in vertical direction, we get
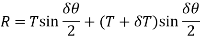

Now, Resolving forces in horizontal direction,
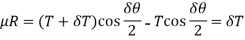
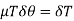
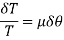
Or 
Now upon integration,
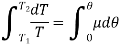
We get the final belt tension ratio.
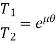
Centrifugal Tension
The centrifugal tension in flat belt is introduced due to its mass, which is denoted here by Tc and given by the formula:
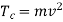
Where, m= mass of the belt per unit length
v = speed of the belt.
Power Transmitted
Power transmitted by the flat belt is given by
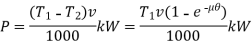
For maximum power transmission
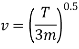
Where, 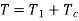
And maximum power is given by,
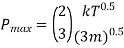
Where, 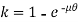
Belt Creep
Slightly higher stretching of belt on tight side then slack side because of difference of tension in both the sides due to which driver pulley receives more length of belt and delivers less length, this process is known as forward creep whereas when driven pulley delivers more length and receives less length of belt is known as backward creep. Creep in belts is given by the given formula;
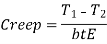
Where, E = modulus of elasticity of belt material.
b and t are width and thickness of belt.
Crowning of pulleys
To prevent the tendency of falling off of the belt from the pulley, face of pulley is provided with a convex curvature, which is known as the crowning of pulley. This phenomenon helps the belt to run in the center of pulley.
Compound Belt Drive
Compound belt drive are the drive in which the driven pulley of first pair of drive is mounted on the same shaft on which driver pulley of second pair is mounted. Such an arrangement of compound belt drive is shown in Figure 5.
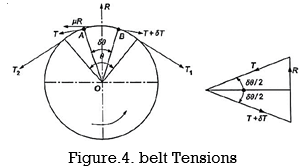
Figure.5. Compound belt drive
Velocity ration for the compound belt dive is given by following relation
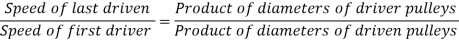
V Belt Drive
These belt drives are generally made of rubber impregnated fabric having v angle between 30-40 degrees. These belt drives are generally used for power transmission from the prime mover.
Clutches are the drives which are used to transmit rotary motion between two coincident shafts when desired.
- Single plate
- Multiplate
Single Plate Clutch
A plate clutch consists of a clutch plate attached to a splined hub which slides freely of the driven side in axial direction. Generally, the clutch plate is made of steel having friction lining on each side.
During engagement clutch plate is firmly pressed against the flywheel by the spring-loaded pressure plate. Whereas during disengagement cover attached to the flywheel is pressed by springs and the flywheel and pressure plate rotates with the input shaft. Figure 6 shows the different parts of single plate clutch.
Torque transmitted by such clutches can be calculated using two criteria which are uniform wear and uniform pressure.
Torque transmitted considering the uniform pressure criteria

Torque transmitted considering the uniform wear criteria
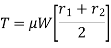
![Single Plate Clutch and Multi Plate Clutch [Descriptive Guide]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643296429_1672156.jpeg)
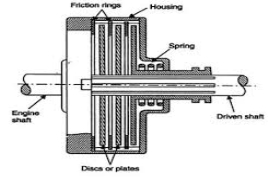
Figure.6. Single plate clutch Figure.7. Multiplate clutch
Multi-Plate Clutch
These kinds of clutches are used at place where limited space is available such as in two wheelers. By increasing the number of plates, the connecting surfaces increase which result in increase in capacity. Figure 7 shows the multiplate clutch.
If n1 be the number of plates on driver shaft and n2 be the number of plates on driven shaft then n will be the number of pairs contact sufraces, which is given by:
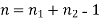
The frictional torque Tis given by
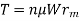
Where, = coefficient of friction
W = Axial load on the clutch
rm = mean radius of friction surface.
For Uniform pressure criteria

For Uniform wear criteria

Cone Clutch
In case of cone clutch, the contact surfaces are in the shape of cone as shown in figure 8. During engagement the surface A and B are in contact completely due the spring pressure applied on the one cone against all other part of the clutch. While during disengagement the cone B is pulled back with the help of a lever system. In these types of clutches, due to the cone shape the normal force on the contact surface is increases.
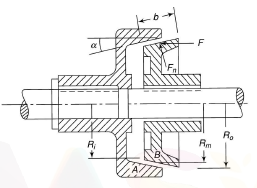
Figure.8. Cone Clutch
In case of cone clutches the frictional torque, T is given by

Where, = coefficient of friction
Fn = Normal force given by

= semi cone angle
Rm = mean radius of friction surface.
Brakes are the friction devices which are used to reduces the speed of a moving vehicle or a machine component. There are several types of brakes are being used which a given below:
Shoe brakes
In this kind of brakes there is a shoe which is pressed against the rotating machine pat to reduce its speed or to stop it by applying friction force using lever mechanism. If only one shoe is used for braking, there is a side thrust on the bearing of the shaft supporting the drum. To avoid this side thrust two shoes are used. Brake shoes are generally made of rubber and wood.
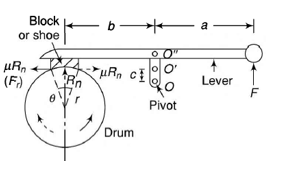
Figure.9. Shoe Brake
Consider figure 9 and it is assumed that the normal reaction and friction forces are being applied at the mid-point of the shoe
Let r =radius of drum
= coefficient of friction
Rn = normal reaction
F = force applied at the lever
Ff = friction force
Braking torque T = friction force Ff × radius
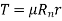
Rn is obtained by equilibrium condition on the shoe, by taking moment about the point O in figure 9.
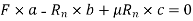
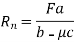
Or

Considering above equation
Case 1: if b=μc, force required to apply brake will be 0 i.e. once the contact between drum and shoe is made the brake will be applied itself. Hence, such brakes are also known as self-locking brakes.
Case 2: as we can see from the equilibrium equation moment of frictional force and the force applied on the lever is in same direction about O, and the friction force is supporting the braking force, hence such brakes are also known as self-energized brakes.
Case 3: if the direction of rotation is reversed the force to be applied on lever will become
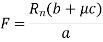
Case 4: if pivot lie on the line of action of friction force, c = 0

Here is taken as constant but if the value of > 40° the coefficient of friction is given by
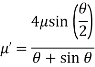
Where outside any trigonometric ratio is to be taken in radians and inside the trigonometric ratio it is to be taken in degrees.
Band and Block Brakes
In this kind of brakes number of wooden blocks are held together with the help of flexible steel band. These wooden blocks are pressed against the drum upon application of brake.
Consider figure 10 we can see a diagram of band and block brake in which each block is subtending an angle 2 at the center of drum. Figure 10 shoes the band and block brake (a) and the forces on the block of the brake (b).
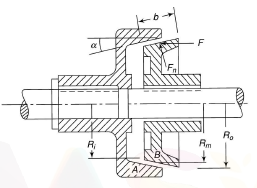
Figure.10. Band and block brake
Let us consider
T0 = tension on the slack side of the band
T1 = tension on the tight side of 1st block
Tn = tension on the tight side of the n blocks
= coefficient of friction
Rn = normal reaction on the block
By applying equilibrium
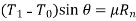
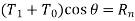
Upon some simplifications we get
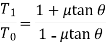
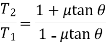
So on,
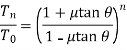
Reference Books
1. Thomas Bevan, Theory of Machines, 3rd edition, CBS Publishers & Distributors, 2005.
2. CleghornW.L. , Mechanisms of Machines, Oxford University Press, 2005.
3. Robert L. Norton, Kinematics and Dynamics of Machinery, Tata McGraw Hill, 2009.
4. Ghosh A. and Mallick A.K., Theory of Mechanisms and Machines, Affiliated East West Pvt. Ltd, New Delhi, 1988.