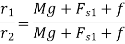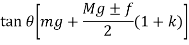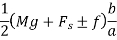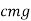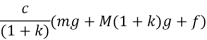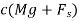Unit 6
Governors
Governor controls the fuel supply or input of the engine. It maintains the supply of fuel as such that at any load either high or low speed of vehicle or machinery remains constant as decided. Generally, governors are used for aircraft and ship propulsion in autopilot mode.
Governors are also used for continuous running heavy machine or powerplant system, where fluctuation of load is a frequent phenomenon. Governors can also be said to be mechanical controlling device. There are two types of governors:
Watt governor is the simplest type of centrifugal governor in which sleeves and arms are assumed to be massless with respect to mass of the balls. If the pivot of the arm coincides with the spindle axis as shown in figure 1(a) is known as fixed pivot watt governor. If arms do not coincide with the spindle axis it is known as open arm pivot as shown in figure 1(b), whereas if arms cross each other, governor is known as cross arm pivot watt governor shown in figure 1(c).

(a) (b) (c)
Figure.1 Types of watt governor
Let us consider m be the mass of balls, r be the radius of governor, h be the height of the governor and it is rotating with an angular velocity of rad/sec.
 From figure 1 by applying the condition of vertical and horizontal equilibrium conditions, we get
From figure 1 by applying the condition of vertical and horizontal equilibrium conditions, we get
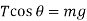
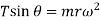
 From above equations, we get
From above equations, we get
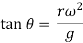
 From figure 1
From figure 1
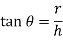
Equating equation 3 and 4
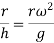
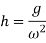
substituting 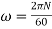 we get
we get
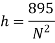
where N is the rpm.
If we introduce a heavy mass at the sleeve, the watt governor becomes the porter governor shown in figure 2.

Figure. 2. Porter governor with the forces on it under action.
Let us assume that m be the mass of balls, M be the mass of sleeve, r is the distance of center of balls from the axis of rotation, f be the force of friction acting on the sleeve which acts in upward direction while sleeve is moving down and in downward direction while sleeve is moving upward. So, force acting on sleeve while moving upward is Mg + f and Mg - f while moving downward. H is the height of governor, I be the instantaneous center of the arm AB and a, b and c are the distances of several points on the governor as shown in figure 2.
Now taking moment about the instantaneous center I and considering equilibrium in the left half of the governor
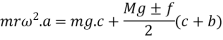
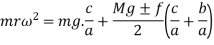
From figure 2
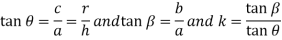
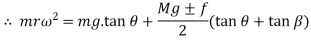
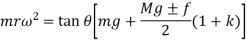
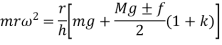

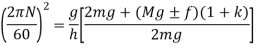
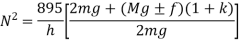
If in figure.2. b=c k=1
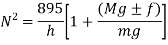
If there is no friction i.e. f=0
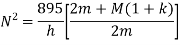
If k=1 and f=0
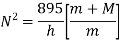
We can see from the above equation that if governor rotates with high rpm even than there is significant change in height which is not possible in case of watt governor.
Proell governor is modified form of the porter governor in which the balls are fixed on upward extension of lower arms of the governor as shown in figure 3.
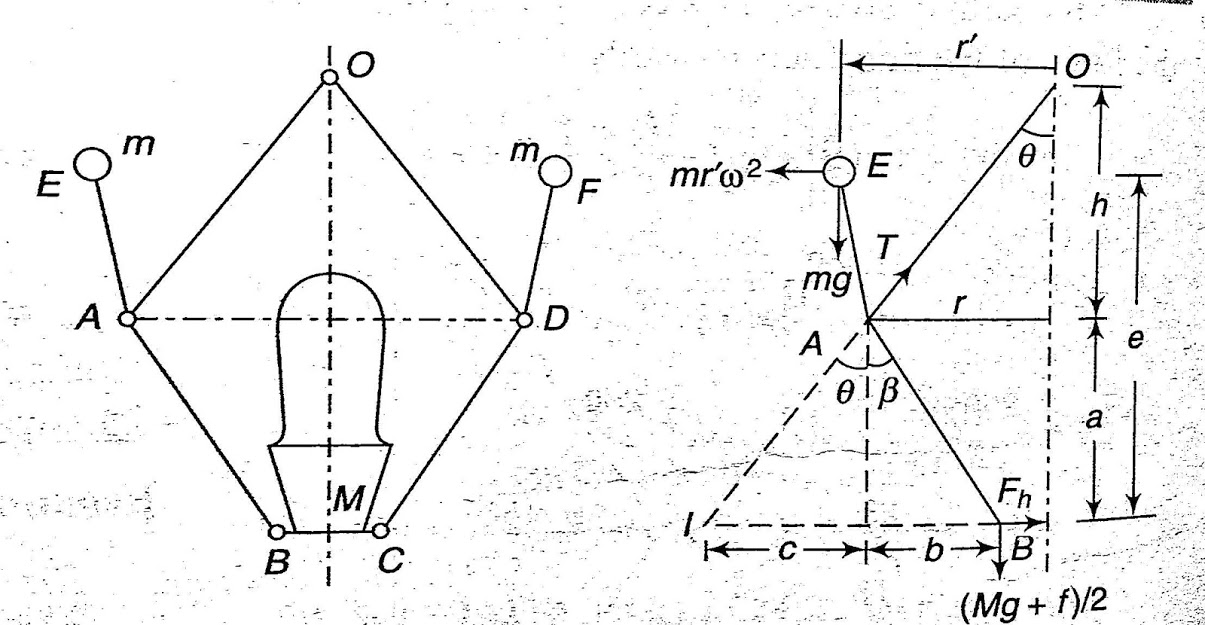
Figure. 2. Proell governor with the forces on it under action.
Considering the equilibrium of left half of the governor, following forces are to be considered
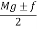
Now taking moment about the instantaneous center of the link on which ball is fixed, I.
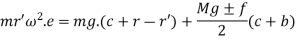
If the balls are in vertical position and neglecting the obliquity we get,
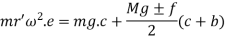
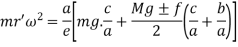
From figure 2
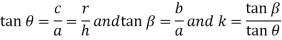
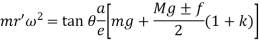
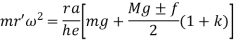
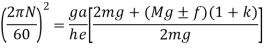
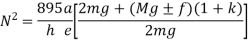
If in figure.2. b=c k=1
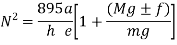
If there is no friction i.e. f=0
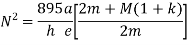
If k=1 and f=0
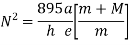
Hartnell governor is the spring-controlled governor in which a pre-compressed spring is used to assist the centrifugal force for controlling the governing action. By using pre-compressed spring, the size of the governor is drastically reduced in terms of radius of rotation of balls. Hartnell governor is very much suitable for smaller machines which runs at very high speed. Different components of a Hartnell governor are shown in figure 3.

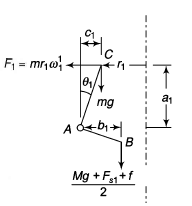
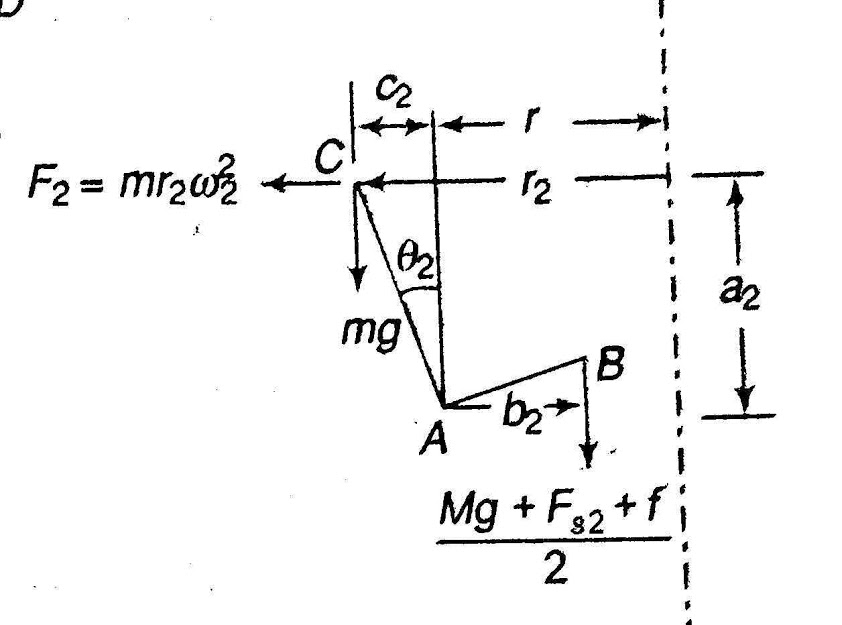
Figure.3. Hartnell Governor and forces on levers
Here it is assumed that in the both the condition of bell-crank lever the sleeve is moving upward direction from initial position and the force of friction is always acting in downward direction.
Let us assume that F be the centrifugal force on the ball, Fs be the spring force on sleeve and f be the friction force.
Now taking moment about the pivot A.
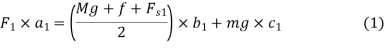
And,
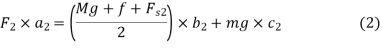
Assuming 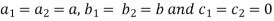
Subtracting equation 1st from 2nd.
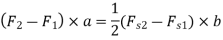
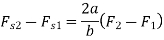
Let h1 be the sleeve moment and s be the stiffness of spring.
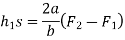
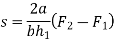
From figure 3
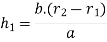
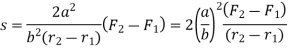
During the governing action of a governor the centrifugal force acting on the balls due to the rotation is balanced by an equal and opposite force on the balls, this radially inward balancing force is known as the controlling force for a governor.
The controlling force is generated by the weight of rotating mass in watt governor, in case of porter governor it is balanced by the weight of rotating mass and mass of sleeve and for Hartnell governor it is caused by the compressed spring.
Value of controlling force different governor is given by:
Porter governor |
|
Hartnell Governor |
|
As we have discussed that the controlling force is equal and opposite to the centrifugal force. Hence, it may be calculated for different radii with the help of expression F=mr2, this expression also indicates that the controlling force is proportional to the radius for a particular speed.
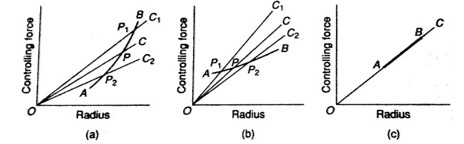
Figure.4 Controlling forces curves for different governors
Figure 4(a) shows the plot of controlling force Ab vs ball radius, here friction force is neglected. In this plot number of lines are being drawn named OC, OC1 and OC2 which provide the value of controlling force for different radii at given speed. In this curve the intersection of the speed curve with controlling force curve gives the speed of governor corresponding to the radii.
Now consider the controlling force curve shown in figure 4(b). in this case point P represents the mean speed of the governor. This plot shows if the speed of governor reaches P1 the radius of ball reaches r1 due to which the necessary action on the throttle valve is done i.e. opening or closing further.
Figure 4(c) shows the controlling force curve AB for spring-controlled governor. From this curve we can observe that such governor can take any radius for a given speed represented by OC. Such governor is known as isochronous.
Effort of a Governor
The mean force acting on the sleeve of a governor to raise and lower it with the change in speed. During operation the force varies from zero to maximum which required to raise or lower the sleeve. Hence, if E is the force required to raise of lower the sleeve then mean force is given by E/2. The effort of the governor is given by:
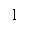 For a porter governor,
For a porter governor,
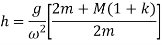
let be increased by c times and E be the applied force on the sleeves to prevent its movement.
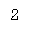 Thus, the force on the sleeve will be (Mg+E).
Thus, the force on the sleeve will be (Mg+E).
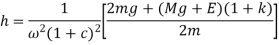
now by dividing 2 by 1.

Subtracting 1 both the sides

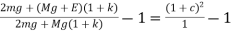
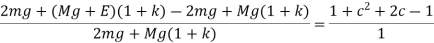
c is very small factor so we can neglect c2.


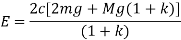
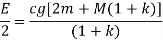
Above expression represent the effort of watt governor if we do not consider the friction. If we substitute the mass of sleeve M equal to 0 and k=1 we get the expression for the effort of the watt governor. Effort for various types of governor is given below:
Watt governor |
|
Porter governor |
|
Hartnell governor |
|
Power of a Governor
The work to be done on the sleeve to change the by a given percentage is known as the Power of a governor, it can be represented by the product of the displacement of the sleeve and effort of the governor.
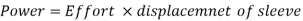
If the height of the governor changes from h to h1 when the speed changes from to (1+c),
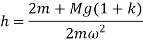
and

Or
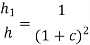
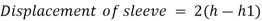

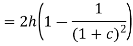
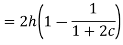

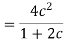
For a porter governor with pivoted joints power is given by:
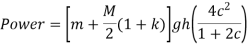
Sensitivity of a governor
An equipment is said to be sensitive if the value of variation or range is having significant vale with respect to the mean value otherwise if variation is negligible with respect to mean value is said to be insensitive. Hence, the sensitivity of a governor is given by the ration of range of speed to the mean speed, and It is represented by S.
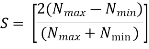
But if the sensitivity of the governor will be too high, it will continuously oscillate between upper stop and lower stop. In such condition the governor will not control the speed of engine rather it operates the engine by switching on and off continuously, this phenomenon of large sensitivity is known as hunting.
Isochronism of a governor
It the variation in the speed of a governor becomes zero the governor is said to be isochronous. This means that for all position of sleeves and balls governor has the same equilibrium speed.
For Porter governor, with all arms equal in length and intersecting on the axis (neglecting friction),
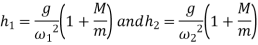
For governor to be isochronous 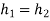 , but if we see above equations it is impossible to have two position of balls for same speed. Hence pendulum governors such as watt, porter and Proell can never be isochronous. But spring governor such as Hartnell can be isochronous.
, but if we see above equations it is impossible to have two position of balls for same speed. Hence pendulum governors such as watt, porter and Proell can never be isochronous. But spring governor such as Hartnell can be isochronous.
For Hartnell governor (neglecting friction)
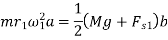
At 2
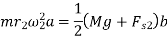
For 1=2,
Condition for a Hartnell governor to be isochronous is: