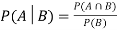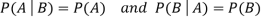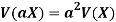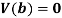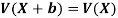Unit - 3
Sample space and Probability
Overview
In many real-life situations when we are unable to forecast the future with complete certainty. That is, in many decisions, we face the uncertainty. This leads to the study and use of the probability theory.
The first attempt to give quantitative measure of probability was made by Galileo (1564-1642), he was an Italian mathematician.
The first foundation was laid by the two mathematicians Pascal and Fermat due to a gambler's dispute in 1654 which led to the creation of a mathematical theory of probability by them. Later, important contributions were made by various researchers including Huygens, Jacob Bernoulli (1654-1705), Laplace (1749-1827), Abraham De-Moivre (1667-1754), and Markov (1856-1922). Thomas Bayes gave an important technical result known as Bayes’ theorem, published after his death in 1763, using which probabilities can be revised on the basis of some new information.
Random Experiment
An experiment in which we know all the possible outcomes but we cannot say that or we cannot predict that which of them will occur when we perform the experiment.
Suppose we toss a coin, we know that what are possible outcomes, it would be head or tail, but we do not know which one of these two will occur.
So, tossing a coin is a random experiment.
Similarly, ‘Throwing a die’ and ‘Drawing a card from a well shuffled pack of 52 playing cards ‘are the examples of random experiment.
Trial
Performing an experiment is called trial, For example-
(i) Throwing a dice
(ii) Tossing a coin
(iii) Picking a playing card
Note-
1. Die: It is a small cube. Dots (number) are marked on its faces. Plural of the die is dice. On throwing a die, the outcome is the number of dots on its upper face.
2. Cards: A pack of cards consists of four suits i.e., Spades, Hearts, Diamonds and Clubs. Each suit consists of 13 cards, nine cards numbered 2, 3, 4, ..., 10, an Ace, a King, a Queen and a Jack or Knave. Colour of Spades and Clubs is black and that of Hearts and Diamonds is red. Kings, Queens and Jacks are known as face cards.
A probability space is a three-tuple (S, F, P) in which the three components are
- Sample space: A non-empty set S called the sample space, which represents all possible outcomes.
- Event space: A collection F of subsets of S, called the event space.
- Probability function: A function P : FR, that assigns probabilities to the events in F.
Odds in favour of an event and odds against an event: If number of favourable ways = m, number of not favourable events = n
(i) Odds in favour of the event 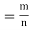
(ii) Odds against the event 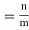
Sample space
Set of all possible outcomes of a random experiment is known as sample space and we denote it by S, and the total number of elements in the sample space is known as size of the sample space and is denoted by n(S).
Discrete sample space- Sample space in which sample points are finite or countably infinite is called discrete sample space.
For example-
- If a die is thrown, then the sample space is
S = {1, 2, 3, 4, 5, 6} and n(S) = 6.
2. If a coin is tossed twice or two coins are tossed simultaneously then the sample space is
S = {HH, HT, TH, TT}
3. If a coin is tossed 4 times or four coins are tossed simultaneously then the sample space is
S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THHT,
THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT} and n(S) = 16.
Note-If a random experiment with x possible outcomes is performed n times, then the total number of elements in the sample is 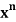
3.1.1 Events and their types
1. Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.
In case of tossing a coin once, S = (H, T) is the sample space. Two outcomes - Head and Tail
- constitute an exhaustive event because no other outcome is possible.
2. Trial and Event: Performing a random experiment is called a trial and outcome is termed as event. Tossing of a coin is a trial and the turning up of head or tail is an event.
3. Equally likely events: Two events are said to be ‘equally likely’, if one of them cannot be expected in preference to the other. For instance, if we draw a card from well-shuffled pack, we may get any card. Then the 52 different cases are equally likely.
4. Independent events: Two events may be independent, when the actual happening of one does not influence in any way the probability of the happening of the other.
5. Mutually Exclusive events: Two events are known as mutually exclusive, when the occurrence of one of them excludes the occurrence of the other. For example, on tossing of a coin, either we get head or tail, but not both.
6. Compound Event: When two or more events occur in composition with each other, the simultaneous occurrence is called a compound event. When a die is thrown, getting a 5 or 6 is a compound event.
7. Favourable Events: The events, which ensure the required happening, are said to be favourable events. For example, in throwing a die, to have the even numbers, 2, 4 and 6 are favourable cases.
Odds in favour of an event and odds against an event-
If the number of favourable cases are ‘m’ and the number or not favourable cases are ‘n’.
Then-
1. Odds in favour of the event = m/n
2. Odds against the event = n/m
3.1.2 Algebra of Events
In a random experiment, let S be the sample space.
Let A  S and B
S and B  S be the events, then we say that-
S be the events, then we say that-
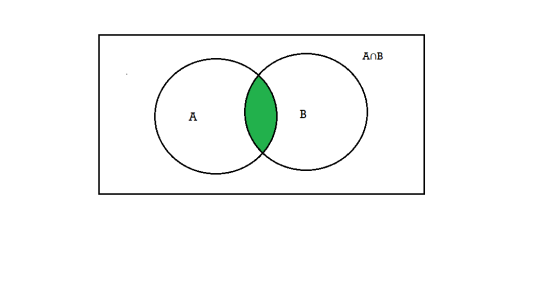
- (A
 B) is an event that occurs only when both A and B occurs.
B) is an event that occurs only when both A and B occurs.
2. (A∪B) is an event that occurs when either one of A or B occurs.
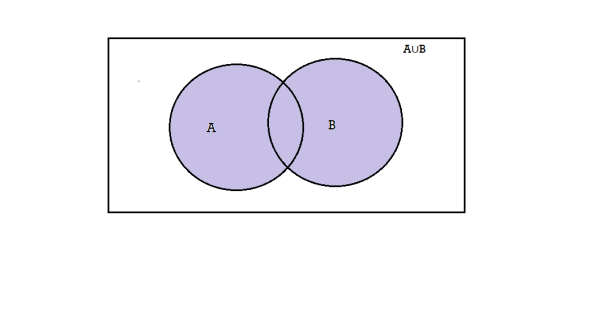
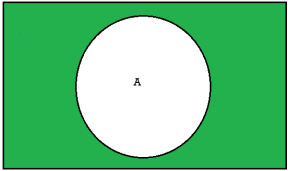
3. A’ is an event that occurs only when A does not occur.
Let S be the sample space of a random experiment and events A and B  S then
S then
P (A  B) = P(A) + P(B) - P (A
B) = P(A) + P(B) - P (A 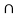 B)
B)
For three non-mutually exclusive events A, B and C, we have
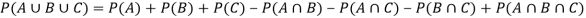
NOTE- If events A and B are mutually exclusive events, then-
P (A 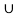 B) = P(A) + P(B)
B) = P(A) + P(B)
For three mutually exclusive events A, B and C, we have
P (A 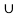 B
B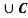 ) = P(A) + P(B) + P(C)
) = P(A) + P(B) + P(C)
Example: 25 lottery tickets are marked with first 25 numerals. A ticket is drawn at random. Find the probability that it is a multiple of 5 or 7.
Sol.
Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.
Therefore,
A = {5, 10, 15, 20, 25}
B = {7, 14, 21}
Here, as A 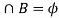
Therefore, A and B are mutually exclusive, and hence
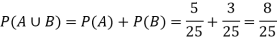
Example: A Card is drawn from a pack of 52 playing cards, find the probability that the drawn card is an ace or a red colour card.
Sol.
Let A be the event that the drawn card is a card of ace and B be the event that it is red colour card. Now as there are four cards of ace and 26 red colour cards in a pack of 52 playing cards. Also, 2 cards in the pack are ace cards of red colour.
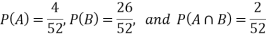
The required probability 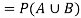
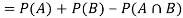
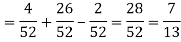
3.1.3 Classical definition of Probability
Classical Definition of Probability
Suppose there are ‘n’ exhaustive cases in a random experiment which is equally likely and mutually exclusive.
Let ‘m’ cases are favourable for the happening of an event A, then the probability of happening event A can be defined as-
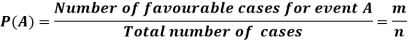
Probability of non-happening of the event A is defined as-
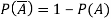
Note- Always remember that the probability of any events lies between 0 and 1.
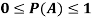
Note- Probability of an impossible event is always zero and that of certain event is 1.
The classical definition of probability fails if-
- The cases are not equally likely
- The number of exhaustive cases is indefinitely large
Expected value-
Let 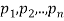 are the probabilities of events and
are the probabilities of events and 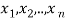 respectively. Then the expected value can be defined as-
respectively. Then the expected value can be defined as-
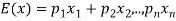
Example1:
In poker, a full house (3 cards of one rank and two of another, e.g., 3 fours and 2 queens) beats a flush (five cards of the same suit).
A player is more likely to be dealt a flush than a full house. We will be able to precisely quantify the meaning of “more likely” here.
Example2:
A coin is tossed repeatedly.
Each toss has two possible outcomes:
Heads (H) or Tails (T)
Both equally likely. The outcome of each toss is unpredictable; so is the sequence of H and T.
However, as the number of tosses gets large, we expect that the number of H (heads) recorded will fluctuate around of the total number of tosses. We say the probability of a H is
of the total number of tosses. We say the probability of a H is  , abbreviated by
, abbreviated by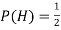 . Of course,
. Of course, 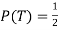 also
also
NOTES:
• In general, an event has associated to it a probability, which is a real number between 0 and 1.
• Events which are unlikely have low (close to 0) probability, and events which are likely have high (close to 1) probability.
• The probability of an event which is certain to occur is 1; the probability of an impossible event is 0.
Example: A bag contains 7 red and 8 black balls then find the probability of getting a red ball.
Sol.
Here total cases = 7 + 8 = 15
According to the definition of probability,
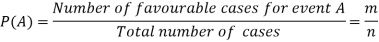
So that, here favourable cases- red balls = 7
Then,
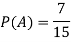
Example: A bag contains 4 red, 5 black and 2 green balls. One ball is drawn from the bag. Find the probability that-
(i) It is a red ball
(ii) It is not black
(iii) It is green or black
Sol.
There are total 11 exhaustive cases.
- We know that, by the definition
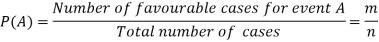
And the favourable cases are 4, then the probability of getting a red ball is-
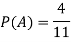
Similarly-
Probability of getting a ball which is not black is-
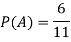
Probability of getting a green or black ball is-
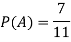
Example: A fair die is thrown. Find the probability of getting
(i) A prime number
(ii) An even number
(iii) A number multiple of 2 or 3
(iv) A number multiple of 2 and 3
(v) A number greater than 4
Sol:
The sample space in this case is- S = {1, 2, 3, 4, 5, 6}
(i) Let E1 be the event of getting a prime number, then E1 = {2, 3, 5}.
P(E1) = 3/6 or ½
(ii) Let E2 be the event of getting an even number, then
E2 = {2, 4, 6}.
P(E2) = 3/6 or ½
(iii) Let E3 be the event of getting an even number, then
E3 = {2, 3, 4, 6}
P(E3) = 4/6 or 2/3
(iv) Let E4 be the event of getting an even number, then
E4 = {6}.
P(E4) = 1/6
(v) Let E5 be the event of getting an even number, then
E4 = {5, 6}.
P(E5) = 2/6 = 1/3
3.1.4 Addition and multiplication law of probability-
Addition law-
If 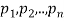 are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by
are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by 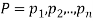
Note-
If two events A and B are not mutually exclusive then the probability of the event that either A or B or both will happen is given by-
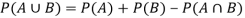
Example: A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white?
Sol.
Here we have two mutually exclusive cases-
1. The first bag is chosen
2. The second bag is chosen
The chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.
So that the probability of drawing a white ball from the first bag is-
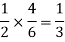
And the probability of drawing a white ball from the second bag is-
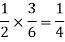
Here the events are mutually exclusive, then the required probability is-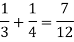
Example-25 lottery tickets are marked with the first 25 numerals. A ticket is drawn at random.
Find the probability that it is a multiple of 5 or 7.
Sol:
Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.
So that
A = {5, 10, 15, 20, 25}
B = {7, 14, 21}
Here, as A 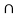 B =
B =  ,
,
A and B are mutually exclusive
Then,
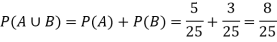
Multiplication law-
For two events A and B-
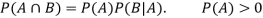
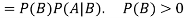
Here 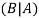 is called conditional probability of B given that A has already happened.
is called conditional probability of B given that A has already happened.
Now-
If A and B are two independent events, then-
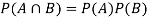
Because in the case of independent events- 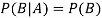
Example: A bag contains 9 balls, two of which are red three blue, and four black.
Three balls are drawn randomly. What is the probability that-
1. The three balls are of different colours
2. The three balls are of the same colours.
Sol.
1. Three balls will be of a different colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
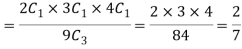
2. Three balls will be of the same colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
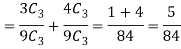
Example: A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?
Sol.
The sample space is- S = {1, 2, 3, 4, 5, 6}
Let A be the event that an outcome is a number that is greater than three and B be the event that it is a prime.
So that-
A = {4, 5, 6} and B = {2, 3, 5} and hence 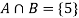
P(A) = 3/6, P(B) = 3/6 and 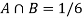
Now the required probability-
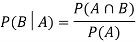
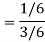
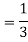
Example: Two cards are drawn from a pack of playing cards in succession with the replacement of the first card. Find the probability that both are the cards of heart.
Sol.
Let A be the event that the first card drawn is a heart and B be the event that the second card is a heart card.
As the cards are drawn with replacement,
Here A and B are independent and the required probability will be-
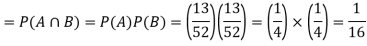
Example: Two male and female candidates appear in an interview for two positions in the same post. The probability that the male candidate is selected is 1/7 and the female candidate selected is 1/5.
What is the probability that-
1. Both of them will be selected
2. Only one of them will be selected
3. None of them will be selected.
Sol.
Here, P (male’s selection) = 1/7
And
P (female’s selection) = 1/5
Then-
1.

2.
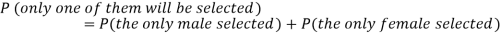
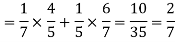
3.

Example: A can hit a target 3 times in 5 shots, B 2 times in 5 shots, and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.
What is the probability that-
1. Two shots hit
2. At least two shots hit
Sol.
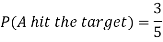
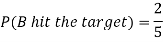
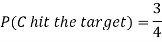
1. Now probability that 2 shots hit the target-
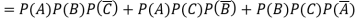
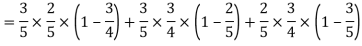
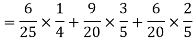
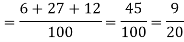
2.
Probability of at least two shots hitting the target
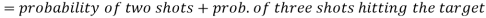
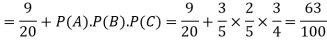
Key takeaways
- Random Experiment- An experiment in which we know all the possible outcomes but we cannot say that or we cannot predict that which of them will occur when we perform the experiment.
2. Exhaustive Events or Sample Space: The set of all possible outcomes of a single performance of an experiment is exhaustive events or sample space. Each outcome is called a sample point.
3. Mutually Exclusive events: Two events are known as mutually exclusive, when the occurrence of one of them excludes the occurrence of the other. For example, on tossing of a coin, either we get head or tail, but not both.
4. If events A and B are mutually exclusive events, then-
P (A  B) = P(A) + P(B)
B) = P(A) + P(B)
5. For three mutually exclusive events A, B and C, we have
P (A  B
B ) = P(A) + P(B) + P(C)
) = P(A) + P(B) + P(C)
6. Probability of an impossible event is always zero and that of certain event is 1
7. Expected value-
Let 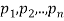 are the probabilities of events and
are the probabilities of events and 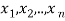 respectively. Then the expected value can be defined as-
respectively. Then the expected value can be defined as-
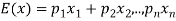
Let A and B be two events of a sample space Sand let 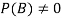 . Then conditional probability of the event A, given B, denoted by
. Then conditional probability of the event A, given B, denoted by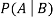 is defined by –
is defined by –
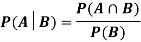
Theorem: If the events A and B defined on a sample space S of a random experiment are independent, then
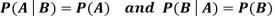
Example1: A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
SOLUTION:
We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for 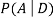 . We know:
. We know:
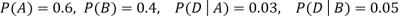
Now,
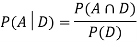
So, we need
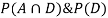
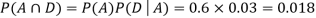
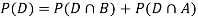
Since, D is the union of the mutually exclusive events 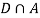 and
and 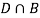 (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)
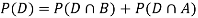
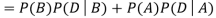
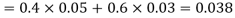
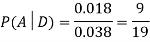
Example2: Two fair dice are rolled, 1 red and 1 blue. The Sample Space is
S = {(1, 1), (1, 2), . . ., (1, 6), . . ., (6, 6)}. Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die shows 2 and the blue one shows 3).
(a) Consider the following events:
A: Red die shows 6.
B: Blue die shows 6.
Find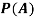 ,
, 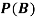 and
and 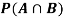 .
.
Solution:
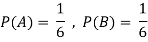
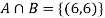
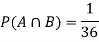
NOTE:
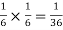 so
so 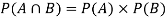 for this example. This is not surprising - we expect A to occur in
for this example. This is not surprising - we expect A to occur in  of cases. In
of cases. In  of these cases i.e., in
of these cases i.e., in 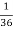 of all cases, we expect B to also occur.
of all cases, we expect B to also occur.
(b) Consider the following events:
C: Total Score is 10.
D: Red die shows an even number.
Find 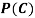 ,
, 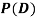 and
and 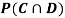 .
.
Solution:
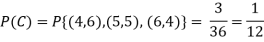
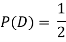
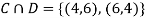
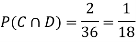
NOTE:
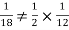 so,
so,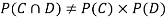 .
.
Why does multiplication not apply here as in part (a)?
ANSWER: Suppose C occurs: so, the outcome is either (4, 6), (5, 5) or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus
Although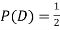 , the probability that D occurs given that C occurs is
, the probability that D occurs given that C occurs is  .
.
We write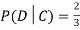 , and call
, and call 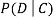 the conditional probability of D given C.
the conditional probability of D given C.
NOTE: In the above example
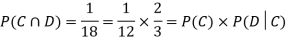
Example3: Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball drawn is red find the probability that it is drawn from the first urn.
Solution:
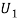 : The ball is drawn from urn I.
: The ball is drawn from urn I.
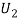 : The ball is drawn from urn II.
: The ball is drawn from urn II.
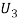 : The ball is drawn from urn III.
: The ball is drawn from urn III.
R: The ball is red.
We have to find 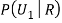
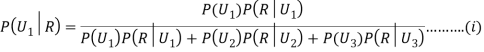
Since the three urns are equally likely to be selected
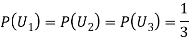
Also,
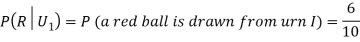
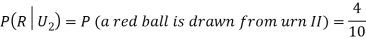
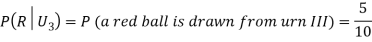
From (i), we have
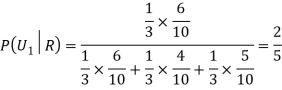
Key takeaways-
Independence of events:
Events are said to be independent if happening or non-happening of any one event is not affected by the happening or non-happening of other events. For example, if a coin is tossed certain number of times, then happening of head in any trial is not affected by any other trial i.e., all the trials are independent.
Two events A and B are independent if and only if P(B|A) = P(B) i.e., there is no relevance of giving any information. Here, if A has already happened, even then it does not alter the probability of B.
If A and B are independent events then-
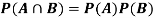
(Two disjoint events are not independent.)
Independence implies that

Knowing that outcome is in B does not change your perception of the outcome’s being in A.
Note-
1. Mutually exclusive events can never be independent.
2. If events A and B are independent then-
- A and B’ are independent
- A’ and B are independent
- A’ and B’ are independent
Example: Two cards are drawn from a pack of cards in succession with replacement of first card. Find the probability that both are the cards of ‘heart’.
Sol.
Let A be the event that the first card drawn is a heart card and B be the event that second card is a heart card.
As the cards are drawn with replacement,
Here A and B are independent and hence the required probability
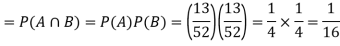
Example: A class consists of 10 boys and 40 girls. 5 of the students are rich and 15 students are brilliant. Find the probability of selecting a brilliant rich boy.
Sol.
Let A be the event that the selected student is brilliant, B be the event that he/she is rich and C be the event that the student is boy.
P(A) = 15/50, P(B) = 5/50 and P(C) = 10/50,
Hence the required probability- [ A, B, C are independent events]
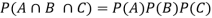
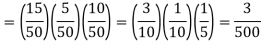
Example: An urn contains 4 red and 7 blue balls. Two balls are drawn one by one without replacement. Find the probability of getting 2 red balls.
Sol:
Let A be the event that first ball drawn is red and B be the event that the second ball drawn is red.
P(A) = 4 /11 and P(B|A) = 3/10
The required probability = P (A and B)
= P(A) P(B|A)
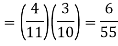
Example: A die is rolled. If the outcome is a number greater than 3, what is the probability that it is a prime number?
Sol:
The sample space of the experiment is
S = {1, 2, 3, 4, 5, 6}
Let A be event that the outcome is a number greater than 3 and B be the event that it is a prime number.
A = {4, 5, 6}, B = {2, 3, 5} and hence
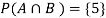
P(A) = 3/6, P(B) = 3/6, 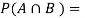 1/6.
1/6.
The required probability = P(B|A)
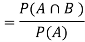
Key takeaways-
- Two events A and B are independent if and only if P(B|A) = P(B)
- If A and B are independent events then-
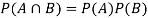
3. Mutually exclusive events can never be independent.
Let S be a sample space and 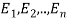 be n mutually exclusive events with P (
be n mutually exclusive events with P (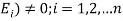 .
.
Let A be an event which is a sub-set of 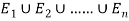 with P(A)>0, then-
with P(A)>0, then-
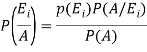
Where i = 1, 2, ……. ,n
And 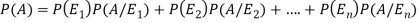 [which is the law of total probability]
[which is the law of total probability]
Example- Three urn contains 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urn is selected randomly and a ball is drawn from it.
If the ball drawn is red then find the probability that it is drawn from the first urn.
Sol.
Let,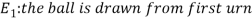
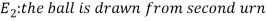
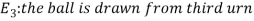
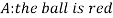
Now we have to find- 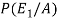
By using Bayes theorem-
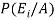 =
= 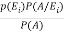
Here three urns equally likely to be selected-
So that-
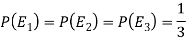
And-
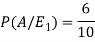
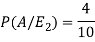
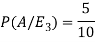
So that-
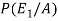 =
= 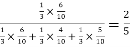
Hence the required probability is 2/5.
Example: A person speaks the truth 3 out of 4 times. A die is thrown. She reports that there are five. What is the chance there is 5?
Sol.
Let 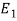 be the event that the person speaks the truth,
be the event that the person speaks the truth, 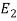 be the event that she tells lie and A be the event that she reports a five.
be the event that she tells lie and A be the event that she reports a five.
So that-
By the law of total probability-
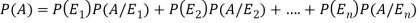
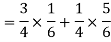
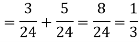
Now we have to find- 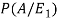
By using Bayes theorem-
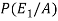 =
= 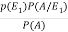
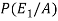 =
= 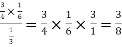
Which is the required probability.
Example: ln a bolt factory machines 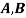 and
and 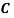 manufacture respectively 25%, 35% and 40% of the total. Lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B.?
manufacture respectively 25%, 35% and 40% of the total. Lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B.?
Solution: bolt is manufactured by machine 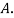
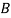 : bolt is manufactured by machine
: bolt is manufactured by machine 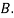
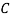 : bolt is manufactured by machine
: bolt is manufactured by machine 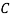
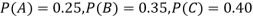
The probability of drawing a defective bolt manufactured by machine 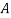 is
is 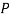 (D/A)
(D/A) 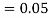
Similarly, 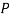 (D/B)
(D/B) 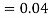 and
and 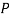 (D/C)
(D/C) 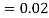
By Baye’s theorem
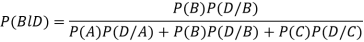
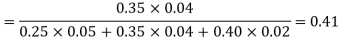
Key takeaways-
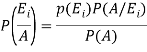
Random variables
A random variable is a real-valued function whose domain is a set of possible outcomes of a random experiment and range is a subset of the set of real numbers and has the following properties:
i) Each particular value of the random variable can be assigned some probability
Ii) Uniting all the probabilities associated with all the different values of the random variable gives the value 1.
A random variable is denoted by X, Y, Z, etc.
For example, if a random experiment E consists of tossing a pair of dice, the sum X of the two numbers which turn up have the value 2,3, 4…12 depending on chance. Then X is a random variable
It is a real valued function which assigns a real number to each sample point in the sample space.
A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability
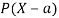
With which X assumes a is defined. Similarly for any interval l the probability
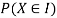
With which X assumes any value in I is defined.
Example:
Tossing a fair coin thrice then-
Sample Space(S) = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
2. Roll a dice
Sample Space(S) = {1,2,3,4,5,6}
A random variable is a real-valued function whose domain is a set of possible outcomes of a random experiment and range is a sub-set of the set of real numbers and has the following properties:
i) Each particular value of the random variable can be assigned some probability
Ii) Uniting all the probabilities associated with all the different values of the random variable gives the value 1.
A random variable is denoted by X, Y, Z etc.
For example, if a random experiment E consists of tossing a pair of dice, the sum X of the two numbers which turn up have the value 2,3, 4…12 depending on chance. Then X is a random variable
Discrete random variable-
A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.
Note- if a random variable takes a finite set of values, it is called discrete and if a random variable takes an infinite number of uncountable values, it is called continuous variable.
Discrete probability distributions-
Let X be a discrete variate which is the outcome of some experiments. If the probability that X takes the values of x is 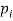 , then-
, then-
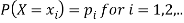
Where-
1. 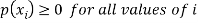
2. 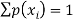
The set of values 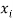 with their probabilities
with their probabilities 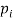 makes a discrete probability distribution of the discrete random variable X.
makes a discrete probability distribution of the discrete random variable X.
Probability distribution of a random variable X can be exhibited as follows-
X | 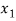 | 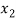 | 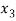 |
P(x) | 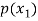 | 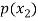 | 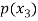 |
Example: Find the probability distribution of the number of heads when three coins are tossed simultaneously.
Sol.
Let be the number of heads in the toss of three coins
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P [X= 0] = P[TTT] = 1/8
P [X = 1] = P [HTT, THH, TTH] = 3/8
P [X = 2] = P [HHT, HTH, THH] = 3/8
P [X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 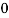 | 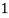 | 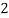 | 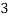 |
P(x) |  |  |  |  |
Example: For the following probability distribution of a discrete random variable X,
X | 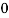 | 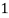 | 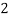 | 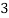 | 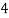 | 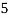 |
P(x) | 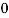 | 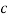 | 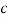 | 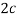 | 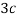 | 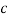 |
Find-
1. The value of c.
2. P[1<x<4]
Sol,
1. We know that-
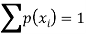
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P [X = 2] + P [X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
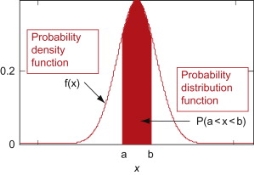
Probability density function
Probability density function (PDF) is an arithmetical appearance which gives a probability distribution for a discrete random variable as opposite to a continuous random variable. The difference among a discrete random variable is that we check an exact value of the variable. Like, the value for the variable, a stock worth, only goes two decimal points outside the decimal (Example 32.22), while a continuous variable has a countless number of values (Example 32.22564879…).
When the PDF is graphically characterized, the area under the curve will show the interval in which the variable will decline. The total area in this interval of the graph equals the probability of a discrete random variable happening. More exactly, since the absolute prospect of a continuous random variable taking on any exact value is zero owing to the endless set of possible values existing, the value of a PDF can be used to determine the likelihood of a random variable dropping within an exact range of values.
Example: The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 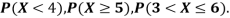
(ii) What will be e minimum value of k so that 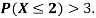
Solution
(i) If X is a random variable, then
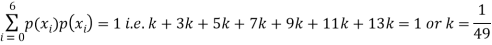
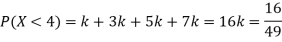
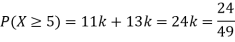
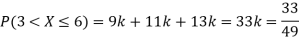
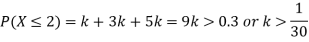
(iii) Thus, minimum value of k=1/30.
Example: A random variate X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | k | 2k | 2k | 3k | 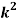 | 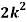 | 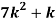 |
(i) Find the value of the k.
(ii) 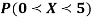
Solution. (i) If X is a random variable, then
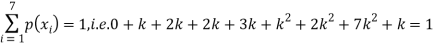
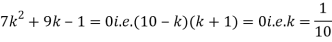
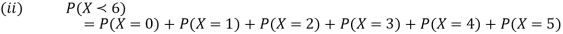
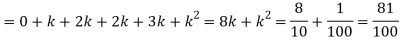
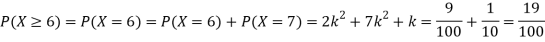
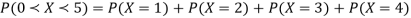
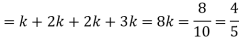
Continuous probability distribution
When a variate X takes every value in an interval it gives rise to continuous distribution of X. The distribution defined by the vidiots like heights or weights are continuous distributions.
A major conceptual difference however exists between discrete and continuous probabilities. When thinking in discrete terms the probability associated with an event is meaningful. With continuous events however where the number of events is infinitely large, the probability that a specific event will occur is practically zero. For this reason, continuous probability statements on must be worth did some work differently from discrete ones. Instead of finding the probability that x equals some value, we find the probability of x falling in a small interval.
Thus the probability distribution of a continuous variate x is defined by a function f (x) such that the probability of the variate x falling in the small interval 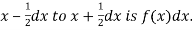 Symbolically it can be expressed as
Symbolically it can be expressed as 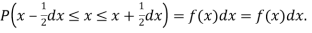 Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.
Thus f (x) is called the probability density function and then continuous curve y = f(x) is called the probability of curve.
The range of the variable may be finite or infinite. But even when the range is finite, it is convenient to consider it as infinite by opposing the density function to be zero outside the given range. Thus, if f (x) =(x) be the density function denoted for the variate x in the interval (a, b), then it can be written as
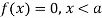
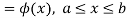
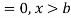
The density function f (x) is always positive and 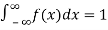 (i.e., the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).
(i.e., the total area under the probability curve and the the x-axis is is unity which corresponds to the requirements that the total probability of happening of an event is unity).
(2) Distribution function
If 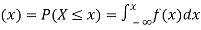
Then F(x) is defined as the commutative distribution function or simply the distribution function the continuous variate X. It is the probability that the value of the variate X will be ≤x. The graph of F(x) in this case is as shown in figure 26.3 (b).
The distribution function F (x) has the following properties
(i) 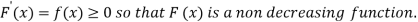
(ii) 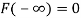
(iii) 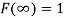
(iv) P (a ≤x ≤b) = 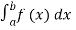 =
= 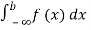 =F (b) – F (a).
=F (b) – F (a).
Example.
(i) Is the function defined as follows a density function?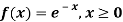
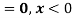
(ii) If so, determine the probability that the variate having this density will fall in the interval (1.2).
(iii) Also find the cumulative probability function F (2)?
Solution. (i) f (x) is clearly ≥0 for every x in (1,2) and
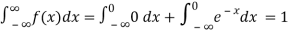
Hence the function f (x) satisfies the requirements for a density function.
(ii)Required probability = 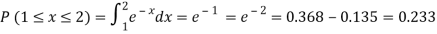
This probability is equal to the shaded area in figure 26.3 (a).
(iii)Cumulative probability function F (2)
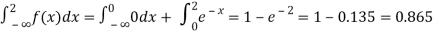
Which is shown in figure
Example: Show that the following function can be defined as a density function and then find 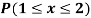 .
.
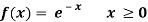

Sol.
Here
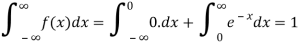
So that, the function can be defined as a density function.
Now.
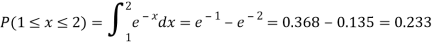
Example: Let X be a continuous random variable with PDF given by
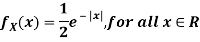
If 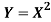 , find the CDF of Y.
, find the CDF of Y.
Solution. First, we note that 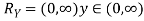 , we have
, we have
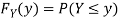
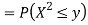
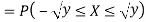
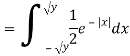
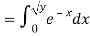
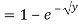
Thus, 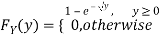
Example: Let X be a continuous random variable with PDF
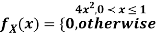
Find 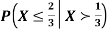 .
.
Solution. We have 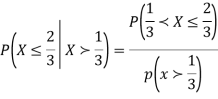
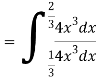
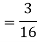
Key takeaways-
- A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.
2. 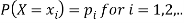
Where-
1. 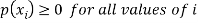
Mathematical expectation
Let a random variable X has a probability distribution which assumes the values say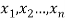 with their associated probabilities
with their associated probabilities 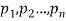 then the mathematical expectation can be defined as-
then the mathematical expectation can be defined as-
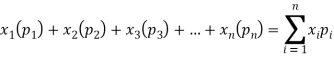
The expected value of a random variable X is written as E(X).
The expected value for a continuous random variable is
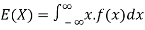
The mean value (μ) of the probability distribution of a variate X is commonly known as its expectation current is denoted by E (X). If f(x) is the probability density function of the variate X, then
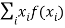 (Discrete distribution)
(Discrete distribution)
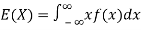 (Continuous distribution)
(Continuous distribution)
In general expectation of any function is 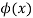 given by
given by
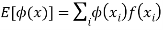 (Discrete distribution)
(Discrete distribution)
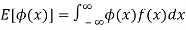 (Continuous distribution)
(Continuous distribution)
(2) Variance offer distribution is given by
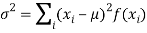 (Discrete distribution)
(Discrete distribution)
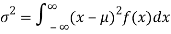 (Continuous distribution)
(Continuous distribution)
Where 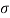 is the standard deviation of the distribution.
is the standard deviation of the distribution.
(3) The rth moment about mean (denoted by 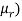 is defined by
is defined by
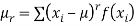 (Discrete function)
(Discrete function)
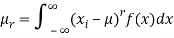 (Continuous function)
(Continuous function)
(4) Mean deviation from the mean is given by
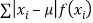 (Discrete distribution)
(Discrete distribution)
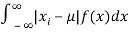 (Continuous distribution)
(Continuous distribution)
Properties of expectation:
- E(k) = k, where k is a constant
- E(kX) = kE(X), k being a constant.
- E (aX + b) = aE(X) + b, where a and b are constants
Example: If a random variable X has the following probability distribution in the tabular form, then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | ½ | ¼ |
Sol.
We know that-
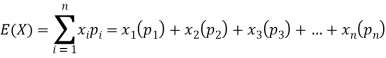
So that-
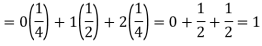
Example: Find the expectations of the number of an unbiased die when thrown.
Sol. Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P [X = 1] = P [X = 2] = P [X = 3] = P [X = 4] = P [X = 5] = P [X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
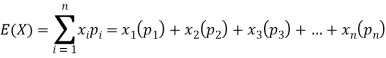
So that-
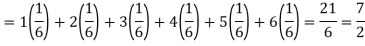
Example: If it rains, a rain coat dealer can earn Rs 500 per day. If it is a dry day, he can lose Rs 100 per day. What is his expectation, if the probability of rain is 0.4?
Sol.
Let X be the amount earned on a day by the dealer. Therefore, X can take the values Rs 500, -Rs 100
Loss of 100 Rs is equivalent to -100 Rs
| Rainy day | Dry day |
X (in Rs) | 500 | -100 |
p(x) | 0.4 | 0.6 |
Hence the expectation of the amount earned-
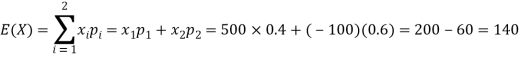
Thus, his expectation is Rs 140, i.e., on an overage he earns Rs 140 per day.
Example. In a lottery, m tickets are drawn at a time out of a ticket numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
Solution. Let 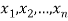 be the variables representing the numbers on the first, second…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
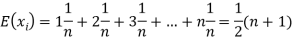
Therefore, the expected value of the sum of the numbers on the tickets drawn
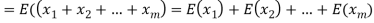
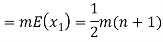
Example. X is a continuous random variable with probability density function given by
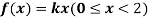
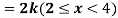
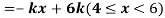
Find k and mean value of X.
Solution. Since the total probability is unity.
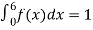
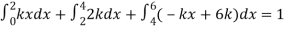
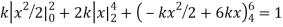
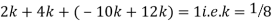
Mean of X =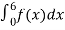
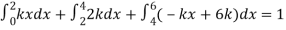
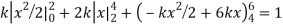
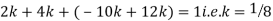
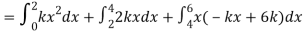
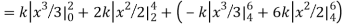
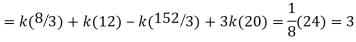
Example. The frequency distribution of a measurable characteristic varying between 0 and 2 is as under
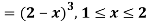
Calculate two standard deviation and also the mean deviation about the mean.
Solution. Total frequency N =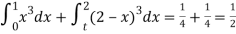
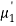 (About the origin) =
(About the origin) =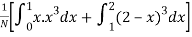
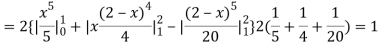
 (About the origin) =
(About the origin) = 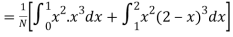
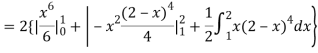
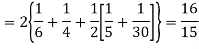
Hence, 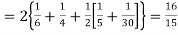
i.e., standard deviation 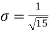
Mean derivation about the mean
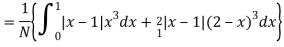
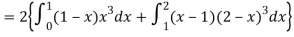
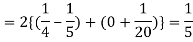
Variance
Variance of a random variable X is defined as the second order central moment and it is defined as-
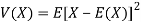
Or
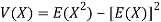
Note-
If X is a random variable, then-
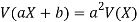
Where a and b are constants.
Note-
Example: Find the following of the given probability distribution-
X | -2 | -1 | 0 | 1 | 2 |
p(x) | 0.15 | 0.30 | 0 | 0.30 | 0.25 |
- V(X)
- V (2X + 3)
Sol.
- We know that-
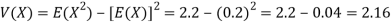
2. V (2X + C) = 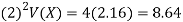
Key takeaways
- The mathematical expectation can be defined as-
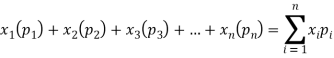
2. The expected value for a continuous random variable is
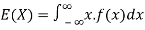
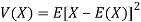
Or
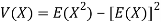
3. If X is a random variable, then-
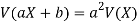
Where a and b are constants.
Moments are the statistical tools used to describe the characteristics of a distribution. The moments of a distribution are the arithmetic means of the various powers of the deviations of items from some given number.
Moments about mean [Central moments]
If x1, x2, ..., xn are the values of the variable under consideration, the r’th moment 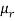 about mean is defined as
about mean is defined as
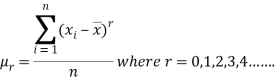
Moments about mean for a frequency distribution
If x1, x2, ..., xn are the values of a variable x with the corresponding frequencies f1, f2, ..., fn respectively then r’th moment 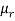 about the mean is defined as
about the mean is defined as
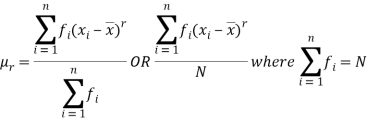
In particular
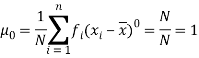
Hence for any distribution, note it here
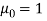
Now for r = 1
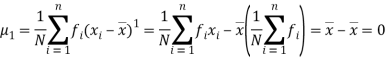
Hence for any distribution,
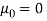
For r = 2

Similarly
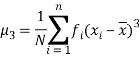
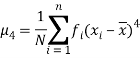
And so on.
Moments about an arbitrary number [Raw moments]
If x1, x2, ..., xn are the values of the variable under consideration, the r’th moment 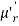 about the number x = a is defined as
about the number x = a is defined as
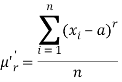
Relation between moments about mean and moment about any point:
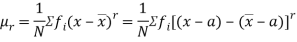
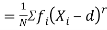 where
where 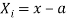 and
and 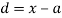
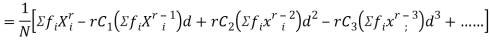
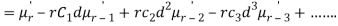
In particular
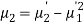
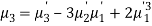
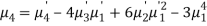
Note-
1. The sum of the coefficients of the various terms on the right-hand side is zero.
2. The dimension of each term on right hand side is the same as that of terms on the left.
Moment generating function (mgf)
The moment generating function of the variate 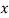 about
about 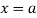 is defined as the expected value of
is defined as the expected value of 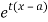 and is denoted
and is denoted 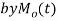 .
.
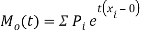
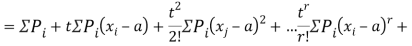
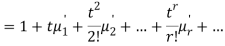
Where 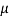 , ‘is the moment of order
, ‘is the moment of order 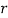 about
about 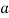
Hence 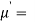 coefficient of
coefficient of 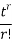 or
or 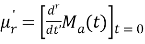
Again 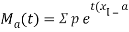 )
) 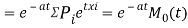
Thus, the moment generating function about the point 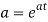 moment generating function about the origin.
moment generating function about the origin.
SKEWNESS:
Skewness denotes the opposite of symmetry. It is lack of symmetry. In a symmetrical series, the mode, the median, and the arithmetic average are identical.
Coefficient of skewness 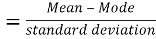
KURTOSIS: It measures the degree of peakiness of a distribution and is given by Measure of kurtosis.
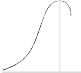
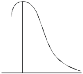
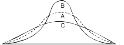
Negative skewness Positive skewness
A. Mesokurtic B. Leptokurtic C. Playkurtic
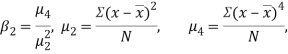
If 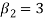 , the curve is normal or mesokurtic.
, the curve is normal or mesokurtic.
If 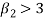 , the curve is peaked or leptokurtic.
, the curve is peaked or leptokurtic.
If 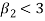 , the curve is flat topped or platykurtic
, the curve is flat topped or platykurtic
Example: Calculate the first four moments of the data given below
Marks | 5-15 | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 |
Students | 10 | 20 | 25 | 20 | 15 | 10 |
Sol:
Marks | Students (f) | (x) | 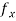 | 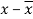 | 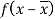 | 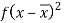 | 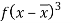 | 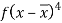 |
5-15 15-25 25-35 35-45 45-55 55-65 | 10 20 25 20 15 10 | 10 20 30 40 50 60 | 100 400 750 800 750 600 | -24 -14 -4 6 16 26 | -240 -280 -100 120 240 360 | 5760 3920 400 720 3840 6760 | -138240 -54880 -1600 4320 61440 175760
| 3317760 768320 6400 25920 983040 4569760 |
| N=100 |
| 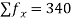 |
| 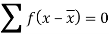 | 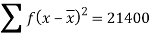 | 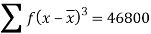 | 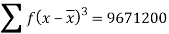 |
The mean will be-
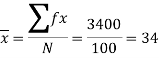
We know that
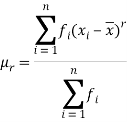
Then
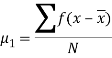
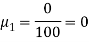
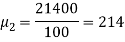
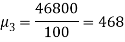
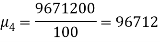
Key takeaways
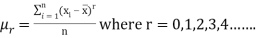
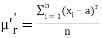
- Relation between moments about mean and moment about any point:
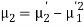
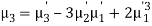
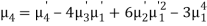
4. The sum of the coefficients of the various terms on the right-hand side is zero.
5. The dimension of each term on right hand side is the same as that of terms on the left.
6. The moment generating function of the variate 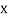 about
about 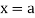 is defined as the expected value of
is defined as the expected value of 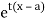 and is denoted
and is denoted 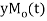 .
.
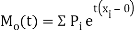
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- IGNOU
- Fundamentals of mathematical statistics by SC Gupta and VK kapoor