Unit - 5
Correlation and regression analysis
Basically, correlation is the measurement of the strength of a linear relationship between two variables.
In other words, we define the correlation as- if the change in one variable affects a change in other variable, then these two variables are said to be correlated.
For example:
- The correlation between a person’s income and expenditures.
- As the temperature goes up, the demand of ice cream also goes up.
Types of correlation
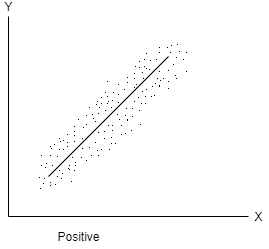
Positive correlation- When both variables move in the same direction, or if the increase in one variable results in a corresponding increase in the other one is called positive correlation.
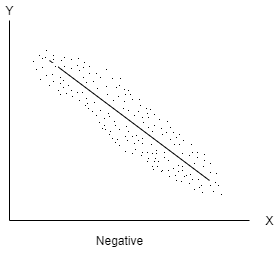
Negative correlation- When one variable increases and other decreases or vice-versa, then the variables said to be negatively correlated.
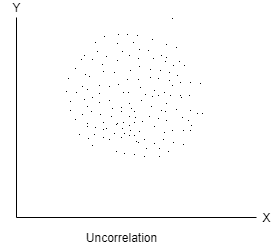
No correlation- When two variables are independent and do not affect each other then there will be no correlation between the two and said to be un-correlated.
Note- (Perfect correlation)- When a variable changes constantly with the other variable, then these two variables are said to be perfectly correlated.
Scatter plots or dot diagrams
Scatter or dot diagram is used to check the correlation between the two variables.
It is the simplest method to represent a bivariate data.
When the dots in diagram are very close to each other, then we can say that there is a fairly good correlation.
If the dots are scattered then we get a poor correlation.
Karl Pearson’s coefficient of correlation
Karl Person’s coefficient of correlation is also called product moment correlation coefficient.
It is denoted by ‘r’, and defined as-
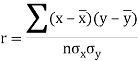
Here 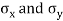 are the standard deviations of these series.
are the standard deviations of these series.
Alternate formula-
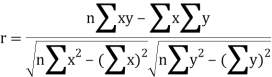
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Value of correlation coefficient (r) | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Example: The data given below is about the marks obtained by a student and hours she studied.
Find the correlation coefficient between hours and marks obtained.
Hours | 1 | 3 | 5 | 7 | 8 | 10 |
Marks | 8 | 12 | 15 | 17 | 18 | 20 |
Solution:
Let hours = x and marks = y
Hours(x) | Marks(y) | 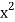 | 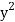 | Xy |
1 | 8 | 1 | 64 | 8 |
3 | 12 | 9 | 144 | 36 |
5 | 15 | 25 | 225 | 75 |
7 | 17 | 49 | 289 | 119 |
8 | 18 | 64 | 324 | 144 |
10 | 20 | 100 | 400 | 200 |
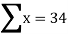 | 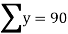 | 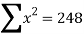 | 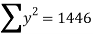 | 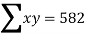 |
Karl Person’s coefficient of correlation is given by-
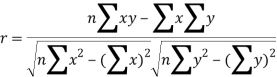
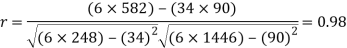
The correlation coefficient between hours and marks obtained is-
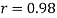
Example: Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
Sol.
x | y | 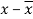 | 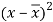 | 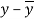 | 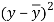 | ( 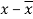 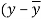 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
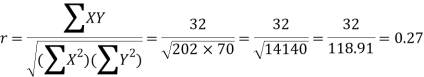
Here the correlation coefficient is 0.27. Which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Example: Ten students got the following percentage of marks in Economics and Statistics
Calculate the 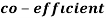 of correlation.
of correlation.
Roll No. |  |  |  | 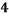 | 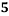 | 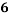 | 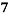 |  | 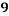 | 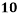 |
Marks in Economics | 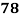 | 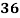 | 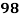 | 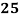 | 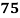 | 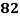 | 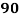 | 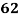 | 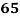 | 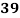 |
Marks in 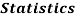 | 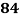 | 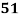 | 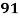 | 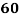 | 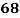 | 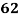 | 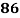 | 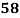 | 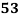 | 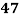 |
Solution:
Let the marks of two subjects be denoted by 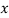 and
and 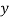 respectively.
respectively.
Then the mean for 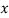 marks
marks 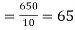 and the mean ofy marks
and the mean ofy marks 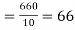
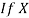 and
and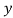 are deviations of x’s and
are deviations of x’s and 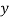 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
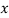 | 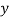 | 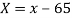 | 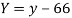 | 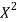 | 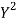 | 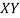 |
78 36 98 25 75 82 90 62 65 39 | 84 51 91 60 68 62 86 58 53 47 | 13 -29 33 -40 10 17 25 -3 0 -26 | 18 -15 25 -6 2 -4 20 -8 -13 -19 | 169 841 1089 1600 100 289 625 9 0 676 | 324 225 625 36 4 16 400 64 169 361 | 234 435 825 240 20 -68 500 24 0 494 |
650 | 660 | 0 | 0 | 5398 | 2224 | 2704 |
Here 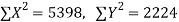
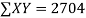
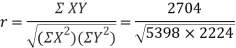
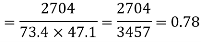
Short-cut method to calculate correlation coefficient-
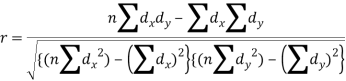
Here,
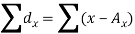
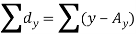
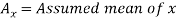
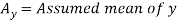
Example: Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
Sol.
X | Y | 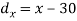 | 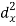 | 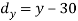 | 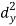 | 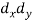 |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
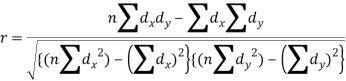
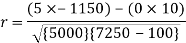
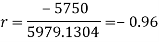
Regression-
If the scatter diagram indicates some relationship between two variables 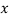 and
and 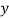 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve ofregression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve ofregression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Or in other words, Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Note- regression line is the best fit line which expresses the average relation between variables.
LINE OF REGRSSION
When the curve is a straight line, it is called a line of regression. A line of regression is the straight line which gives the best fit in the least square sense to the given frequency.
Equation of the line of regression-
Let
y = a + bx …………. (1)
Is the equation of the line of y on x.
Let 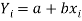 be the estimated value of
be the estimated value of 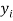 for the given value of
for the given value of 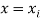 .
.
So that, according to the principle of least squares, we have the determined ‘a’ and ‘b’ so that the sum of squares of deviations of observed values of y from expected values of y,
That means-
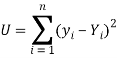
Or
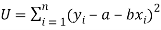 …….. (2)
…….. (2)
Is minimum.
Form the concept of maxima and minima, we partially differentiate U with respect to ‘a’ and ‘b’ and equate to zero.
Which means
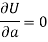
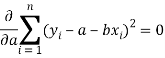
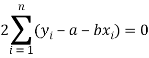
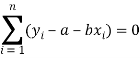
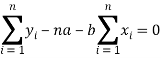
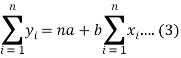
And
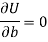
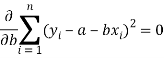
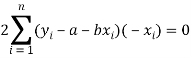
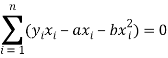
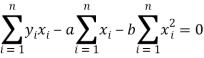
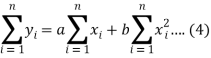
These equations (3) and (4) are known as normal equation for straight line.
Now divide equation (3) by n, we get-
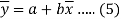
This indicates that the regression line of y on x passes through the point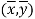 .
.
We know that-
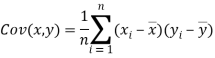
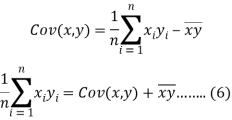
The variance of variable x can be expressed as-
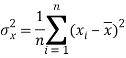
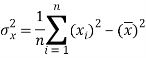
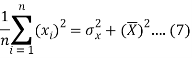
Dividing equation (4) by n, we get-
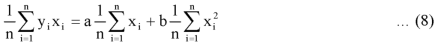
From the equation (6), (7) and (8)-
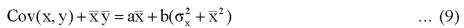
Multiply (5) by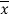 , we get-
, we get-
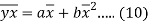
Subtracting equation (10) from equation (9), we get-
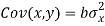
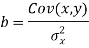
Since ‘b’ is the slope of the line of regression y on x and the line of regression passes through the point (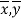 ), so that the equation of the line of regression of y on x is-
), so that the equation of the line of regression of y on x is-
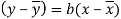
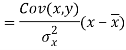
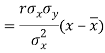
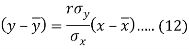
This is known as regression line of y on x.
Note-
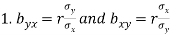 are the coefficients of regression.
are the coefficients of regression.
2. 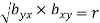
Example: Two variables X and Y are given in the dataset below, find the two lines of regression.
X | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
Y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
Sol.
The two lines of regression can be expressed as-
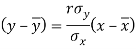
And
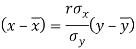
X | y | 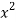 | 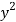 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
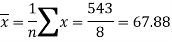
And
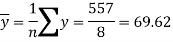
Standard deviation of x-
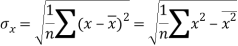

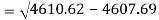
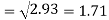
Similarly-
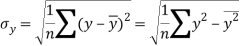
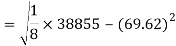
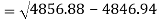
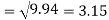
Correlation coefficient-
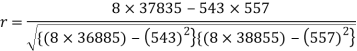
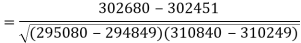
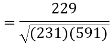
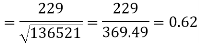
Put these values in regression line equation, we get
Regression line y on x-
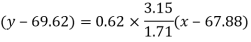
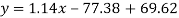
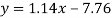
Regression line x on y-
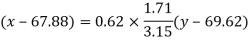
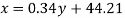
Regression line can also be found by the following method-
Example: Find the regression line of y on x for the given dataset.
X | 4.3 | 4.5 | 5.9 | 5.6 | 6.1 | 5.2 | 3.8 | 2.1 |
Y | 12.6 | 12.1 | 11.6 | 11.8 | 11.4 | 11.8 | 13.2 | 14.1 |
Sol.
Let y = a + bx is the line of regression of y on x, where ‘a’ and ‘b’ are given as-
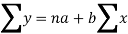
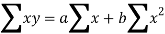
We will make the following table-
x | Y | Xy | 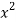 |
4.3 | 12.6 | 54.18 | 18.49 |
4.5 | 12.1 | 54.45 | 20.25 |
5.9 | 11.6 | 68.44 | 34.81 |
5.6 | 11.8 | 66.08 | 31.36 |
6.1 | 11.4 | 69.54 | 37.21 |
5.2 | 11.8 | 61.36 | 27.04 |
3.8 | 13.2 | 50.16 | 14.44 |
2.1 | 14.1 | 29.61 | 4.41 |
Sum = 37.5 | 98.6 | 453.82 | 188.01 |
Using the above equations we get-
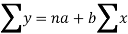
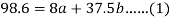
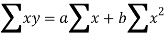
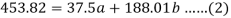
On solving these both equations, we get-
a = 15.49 and b = -0.675
So that the regression line is –
y = 15.49 – 0.675x
Note – Standard error of predictions can be found by the formula given below-
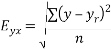
Difference between regression and correlation-
1. Correlation is the linear relationship between two variables while regression is the average relationship between two or more variables.
2. There are only limited applications of correlation as it gives the strength of linear relationship while the regression is to predict the value of the dependent varibale for the given values of independent variables.
3. Correlation does not consider dependent and independent variables while regression consider one dependent variable and other indpendent variables.
Key takeaways-
- Karl Pearson’s coefficient of correlation-
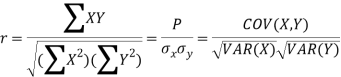
2. Perfect Correlation: If two variables vary in such a way that their ratio is always constant, then the correlation is said to be perfect.
3. Short-cut method to calculate correlation coefficient-
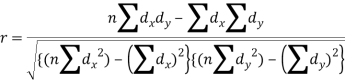
4. Spearman’s rank correlation-
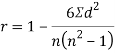
5. The variable which is used for prediction is called independent variable. It is known as predictor or regressor.
6. Regression line is the best fit line which expresses the average relation between variables.
7. Regression line of y on x.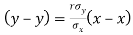
Spearman’s rank correlation-
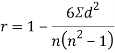
Solution. Let 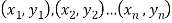 be the ranks of
be the ranks of 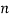 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 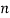 and hence their arithmetic means are, each
and hence their arithmetic means are, each
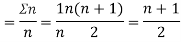
Let 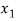 ,
, 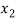 ,
, 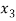 ,
, 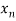 be the values of variable
be the values of variable 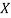 and
and 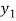 ,
, 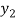 ,
, 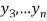 those of
those of 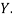
Then 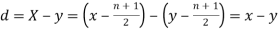
Where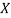 and y are deviations from the mean.
and y are deviations from the mean.
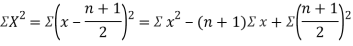
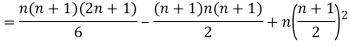
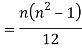
Clearly, 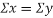 and
and 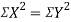
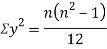
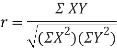
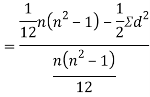
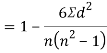
SPEARMAN’S RANK CORRELATION COEFFICIENT:
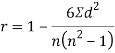
Where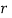 denotes rank coefficient of correlation and
denotes rank coefficient of correlation and 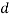 refers to the difference ofranks between paired items in two series.
refers to the difference ofranks between paired items in two series.
Example: Compute the Spearman’s rank correlation coefficient of the dataset given below-
Person | A | B | C | D | E | F | G | H | I | J |
Rank in test-1 | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in test-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Sol.
Person | Rank in test-1 | Rank in test-2 | d = 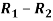 | 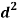 |
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
Sum |
|
|
| 280 |
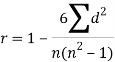
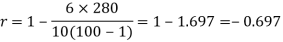
Example: If X and Y are uncorrelated random variables, 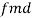 the
the 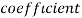 of correlation between
of correlation between  and
and 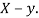
Solution.
Let 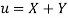 and
and 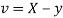
Then 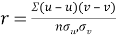
Now 
Similarly, 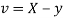
Now 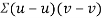
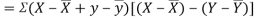
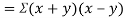
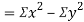
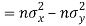
Also 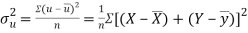
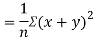
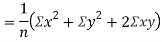
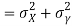 (As
(As 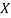 and
and 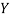 are not correlated, we have
are not correlated, we have 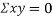 )
)
Similarly, 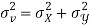
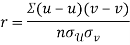
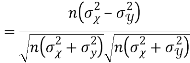
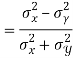
Maximum likelihood estimate is the method of estimation which was formulated by C.F. Gauss.
First, we will define likelihood function-
Likelihood function- Let 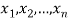 be a random sample of size n from a population with density function f (x.
be a random sample of size n from a population with density function f (x. 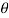 ). Then the likelihood function of the sample values
). Then the likelihood function of the sample values 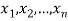 . Usually denoted by L = L (
. Usually denoted by L = L (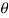 ) is their joint density function; given-by
) is their joint density function; given-by
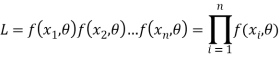
L gives the relative likelihood that the random variables assume a particular set of values 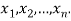 For a given sample
For a given sample 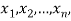 L becomes a function of the variable
L becomes a function of the variable 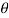 , the parameter.
, the parameter.
The principle of maximum likelihood consists in finding an estimator for the unknown parameter 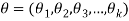 say, which maximizes the likelihood function L (
say, which maximizes the likelihood function L (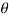 ) for variations in parameter.
) for variations in parameter.
It means we have to find
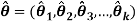
So that
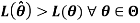
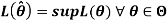
1bus if there exists a function 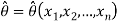 of the sample values which maximizes L for variations in
of the sample values which maximizes L for variations in 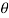 , then
, then 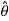 is to be taken as an estimator of
is to be taken as an estimator of 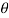 .
.
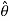 is usually called maximum likelihood estimator (MLE).
is usually called maximum likelihood estimator (MLE).
Thus 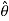 is the solution, if any of the following
is the solution, if any of the following
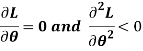
Since L > 0, and lQg L is a non-decreasing function of L; L and log L attain their extreme values (maxima or minima) 'at the same value of 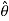
The first of the above equations can be written as
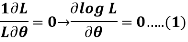
If 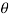 is vector valued parameter. Then
is vector valued parameter. Then 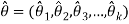 , is given by the solution of simultaneous equations
, is given by the solution of simultaneous equations
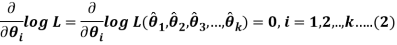
Equations 1 and 2 are usually referred to as the Likelihood equations for estimating the parameters.
Important notes of MLE
1. Cramer-Rao theorem- With probability approaching unity as n tends to infinity, the likelihood equation 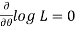 , has a solution which converges in probability to the true value
, has a solution which converges in probability to the true value 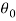 . In other words, we can say that MLE’s are consistent.
. In other words, we can say that MLE’s are consistent.
2. MLE's are always consistent estimators but need not be unbiased.
3. Variance of MLE is–
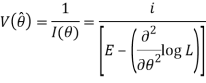
4. If ML.E exists, it is the most efficient in the class of such estimators.
5. If a sufficient estimator exists, it is a function of the Maximum Likelihood Estimator.
Properties of Maximum Likelihood Estimators
1. A ML estimator is not necessarily unique.
2. A ML estimator is not necessarily unbiased.
3. A ML estimator may not be consistent in rare case.
4. If a sufficient statistic exists, it is a function of the ML estimators.
5. When ML estimator exists, then it is most efficient in the group of such estimators.
Example: Prove that the. Maximum likelihood estimates of the parameter a of a population having density function:
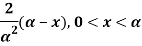
For a sample of, unit size is 2x. x being the sample value. Show also that the estimate is biased.
Sol:
For a random sample of unit size (n = 1). The likelihood function is-
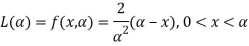
Likelihood equation gives-
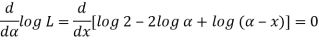
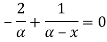
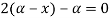
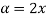
Hence MLE of 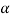 is given by
is given by 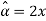
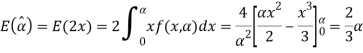
Since 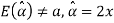 is not an unbiased estimate of
is not an unbiased estimate of 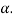
Method of moments
The method of moments was discovered by Karl Pearson.
The principle of this method consists of equating the sample moments to the corresponding moments of the population, which are the function of unknown population parameter.
Here we will equate as many sample moments as there are unknown parameters and solve these simultaneous equations for estimating unknown parameter(s). This method of obtaining the estimate(s) of unknown parameter(s) is called “Method of Moments”.
Suppose 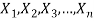 be a random sample of size n taken from a population whose probability density (mass) function is f(x,
be a random sample of size n taken from a population whose probability density (mass) function is f(x, ) with k unknown parameters, say,
) with k unknown parameters, say, 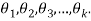
Then the r’th sample moment about origin is
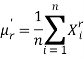
And about mean is
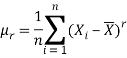
While the rth population moment about origin is
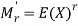
And about mean is
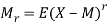
Generally, the first moment about origin (zero) and rest central moments (about mean) are equated to the corresponding sample moments. Thus, the equations are
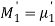
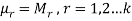
By solving these k equations for unknown parameters, we get the moment estimators.
Properties of Moment Estimators
- The moment estimators are not necessarily unbiased.2
- The moment estimators are generally less efficient than maximum likelihood estimators.
- The moment estimators are asymptotically normally distributed.
- The moment estimators may not be function of sufficient statistics.
- The moment estimators are not unique.
Example: Find the estimator for λ by the method of moments for the exponential distribution whose probability density function is given by
f (x, λ) = (1/λ)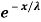 ; x>0 and λ>0
; x>0 and λ>0
Sol:
Let 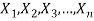
Be a random sample of size n taken from exponential distribution whose probability density function is given by
f (x, λ) = (1/λ)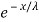 ; x>0 and λ>0
; x>0 and λ>0
We know that the first moment about origin, that is, population mean of
Exponential distribution with parameter λ is
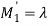
And the corresponding sample moment about origin is
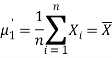
Therefore, by the method of moments, we equate population moment with
Corresponding sample moment. Thus,
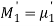
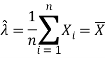
Hence, moment estimator for 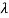 is X.
is X.
Key takeaways
1. Cramer-Rao theorem- With probability approaching unity as n tends to infinity, the likelihood equation 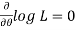 , has a solution which converges in probability to the true value
, has a solution which converges in probability to the true value 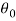 . In other words, we can say that MLE’s are consistent.
. In other words, we can say that MLE’s are consistent.
2. MLE's are always consistent estimators but need not be unbiased.
3. If ML.E exists, it is the most efficient in the class of such estimators.
4. If a sufficient estimator exists, it is a function of the Maximum Likelihood Estimator.
5. When ML estimator exists, then it is most efficient in the group of such estimators.
6. If a sufficient statistic exists, it is a function of the ML estimators.
Confidence interval is an important concept in estimation. There are many problems which need to obtain the confidence interval for population mean.
For example, an investigator may interest to find the interval estimate of average income of the people living in a particular region.
Confidence Interval for Population Mean when Population Variance is Known
Let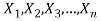 be a random sample of size n taken from normal population N (
be a random sample of size n taken from normal population N (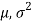 ) when
) when 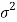 is known.
is known.
To find out the confidence interval for population mean, first of all we search the statistic for estimating μ whose distribution is known.
We know that when parent population is normal N (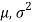 ) then sampling distribution of sample mean
) then sampling distribution of sample mean 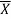 is normally distributed with mean
is normally distributed with mean 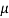 and variance
and variance 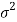 /n.
/n.
The variate
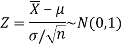
Follows the normal distribution with mean 0 and variance unity. Therefore, the probability density function of Z is
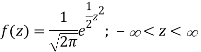
Here we will introduce two constants, 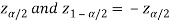
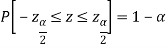
Where, 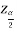 is the value of the variate Z having an area of
is the value of the variate Z having an area of  under the right tail of the probability curve of Z
under the right tail of the probability curve of Z
By putting the value of Z in above equation, we get-
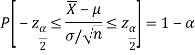
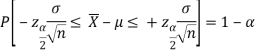
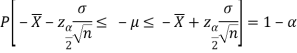
Multiplying each term by (-1) in above inequality, we get
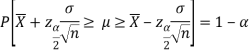
This can be rewritten as
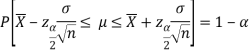
Hence, (1-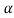 ) 100% confidence interval of population mean is given by
) 100% confidence interval of population mean is given by
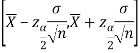
For example, if we take a large sample from a normal population with mean 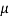 and standard deviation
and standard deviation 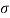 , then
, then
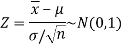
And
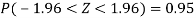
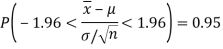
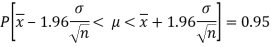
Thus, 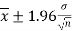 are 95% confidence limits for the unknown parameter
are 95% confidence limits for the unknown parameter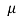 , the population mean and the interval
, the population mean and the interval 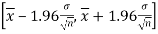 is called the 95% confidence interval.
is called the 95% confidence interval.
Similarly,
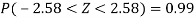
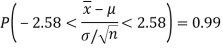

Thus, 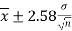 are 99% confidence limits for the unknown parameter
are 99% confidence limits for the unknown parameter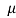 , the population mean and the interval
, the population mean and the interval
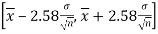 is called the 99% confidence interval.
is called the 99% confidence interval.
Example: The mean life of the bulbs manufactured by a company follows normal distribution with standard deviation 3200 hrs. A sample of 250 bulbs is taken and it is found that the average life of the bulbs is 50000 hrs. With a standard deviation of 3500 hrs. Establish the 99% confidence interval within which the mean life of bulbs of the company is expected to lie.
Sol:
Here, we have
n = 250 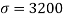 ,
, 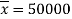 and S = 3500
and S = 3500
Since population standard deviation i.e., population variance 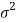 is known,
is known,
Therefore, we use (1-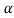 ) 100% confidence limits for population mean when population variance is known which are given by
) 100% confidence limits for population mean when population variance is known which are given by
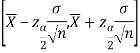
Where 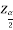 is the value of the variate Z having an area of
is the value of the variate Z having an area of  under the right tail of the probability curve of Z and for 99% confidence interval, we have
under the right tail of the probability curve of Z and for 99% confidence interval, we have
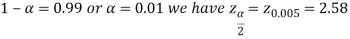
Therefore, the 99% confidence limits are
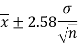
By putting the values of n, 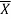 and σ, the 99% confidence limits are
and σ, the 99% confidence limits are
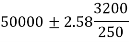
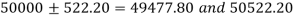
Hence, 99% confidence interval within which the mean life of bulb of the company is expected to lie is [49477.80, 50522.20].
Key takeaways
(1-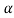 ) 100% confidence interval of population mean is given by
) 100% confidence interval of population mean is given by
Nowadays the concept of p-value became very important part of inferential statistics. It is very important concept as most of the statistical software provides p-value rather than critical value.
p-value provides more information compared to critical value as far as rejection or do not rejection of null hypothesis.
The p-value is the smallest value of level of significance (α) at which a null hypothesis can be rejected using the obtained value of the test statistic and it is defined as below-
The p-value is the probability of obtaining a test statistic equal to or more extreme (in the direction of sporting H1) than the actual value obtained when null hypothesis is true.
While testing a hypothesis, pre-selection of a significance level α does not account for values of test statistics that are “close” to the critical region.
Thus, a test statistic value that is non-significant say for α = 0.05 may become significant for α = 0.01.
p-value approach is designed to give the user an alternative (in terms of probability) to a mere “reject” or “do not reject” conclusion.
P-Value is the lowest level (of significance) at which the observed value of the test statistic is significant.
The p-value also depends on the type of the test.
For right-tailed test:
p-value = P [Test Statistic (T) ≥ observed value of the test statistic]
For left-tailed test:
p-value = P [Test Statistic (T) ≤ observed value of the test statistic]
If test is two-tailed then the p-value is defined as:
For two-tailed test:
p-value = 2P [ T ≥ | observed value of the test statistic|]
How do we take decision about the null hypothesis on the basis of p-value?
We take the decision as mentioned below-
The p-value is compared with level of significance (α) and if p-value is equal or less than, then we reject the null hypothesis and if the p-value is greater than we do not reject the null hypothesis.
Note- Many computers software’s or packages like SPSS, SAS, MINITAB, STATA,
MS-Excel, R programming, Python present the p-value as part of the output for testing of hypotheses.
Key takeaways
- The p-value is the smallest value of level of significance (α) at which a null hypothesis can be rejected using the obtained value of the test statistic
- p-value approach is designed to give the user an alternative (in terms of probability) to a mere “reject” or “do not reject” conclusion.
Chi-square distribution as a test of goodness of fit
When a fair coin is tossed 80 times, we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity 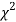 (pronounced as chi squares). If
(pronounced as chi squares). If 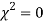 the observed and theoretical frequencies completely agree. As the value of
the observed and theoretical frequencies completely agree. As the value of 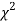 increases, the discrepancy between the observed and theoretical frequencies increases.
increases, the discrepancy between the observed and theoretical frequencies increases.
Definition.
If 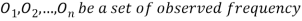 and
and 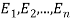 be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then 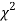 is defined by the relation
is defined by the relation
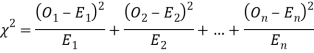
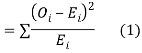
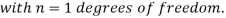
Chi – square distribution
If 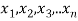 be n independent normal variates with mean zero and s.d. Unity, then it can be shown that
be n independent normal variates with mean zero and s.d. Unity, then it can be shown that  is a random variate having
is a random variate having 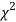 distribution with ndf.
distribution with ndf.
The equation of the 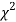 curve is
curve is
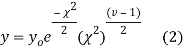
(1) Properties of 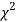 distribution
distribution
- If v = 1, the
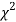 curve (2) reduces to
curve (2) reduces to 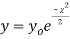 which is the exponential distribution.
which is the exponential distribution. - If
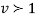 this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2.
this curve is tangential to x – axis at the origin and is positively skewed as the mean is at v and mode at v-2. - The probability P that the value of
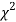 from a random sample will exceed
from a random sample will exceed 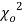 is given by
is given by
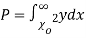
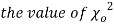 have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
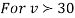 , the
, the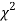 curve approximates to the normal curve and we should refer to normal distribution tables for significant values of
curve approximates to the normal curve and we should refer to normal distribution tables for significant values of 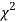 .
.
IV. Since the equation of 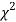 curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
V. Mean = 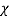 and variance =
and variance = 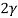
Goodness of fit
The values of 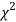 is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution
is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit given distribution 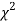 therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory and fact.
This is a nonparametric distribution free test since in this we make no assumptions about the distribution of the parent population.
Procedure to test significance and goodness of fit
(i) Set up a null hypothesis and calculate
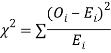
(ii) Find the df and read the corresponding values of 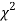 at a prescribed significance level from table V.
at a prescribed significance level from table V.
(iii) From 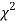 table, we can also find the probability P corresponding to the calculated values of
table, we can also find the probability P corresponding to the calculated values of 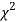 for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of 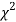 is significant at 5% level of significance
is significant at 5% level of significance
If P<0.01 the value is significant at 1% level.
If P>0.05, it is a good faith and the value is not significant.
Example. A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Solution. For v = 5, we have 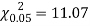
P, probability of getting a head=1/2; q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 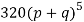
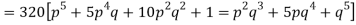
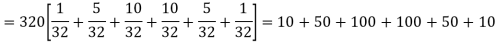
Thus, the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 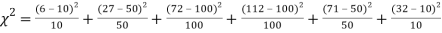
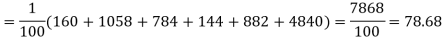
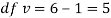
Since the calculated value of 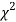 is much greater than
is much greater than 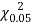 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Example. Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05.
x | 0 | 1 | 2 | 3 | 4 |
f | 419 | 352 | 154 | 56 | 19 |
Solution. Mean m 
Hence, the theoretical frequency is 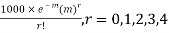
X | 0 | 1 | 2 | 3 | 4 | Total |
F | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 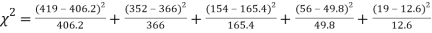
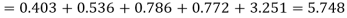
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 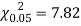
Since the calculated value of 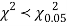 the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
Example. In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
Solution. The corresponding frequencies are
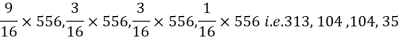
Hence,
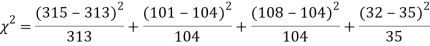
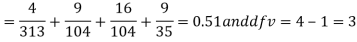
For v = 3, we have 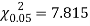
Since the calculated value of 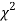 is much less than
is much less than 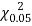 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Key takeaways-
- For testing the null hypothesis, the test statistic t is given by-
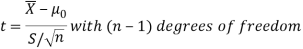
2.
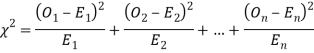
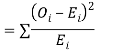
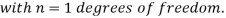
Population-
The population is the collection or group of observations under study.
The total number of observations in a population is known as population size and it is denoted by N.
Types of population-
- Finite population – the population contains finite numbers of observations is known as finite population
- Infinite population- it contains infinite number of observations.
- Real population- the population which comprises the items which are all present physically is known as real population.
- Hypothetical population- if the population consists the items which are not physically present but their existence can be imagined, is known as hypothetical population.
Sample –
To get the information from all the elements of a large population may be time consuming and difficult. And also, if the elements of population are destroyed under investigation, then getting the information from all the units is not make a sense. For example, to test the blood, doctors take very small amount of blood. Or to test the quality of certain sweet we take a small piece of sweet in such situations, a small part of population is selected from the population which is called a sample
Complete survey-
When each and every element of the population is investigated or studied for the characteristics under study then we call it complete survey or census.
Sample Survey-
When only a part or a small number of elements of population are investigated or studied for the characteristics under study then we call it sample survey or sample enumeration Simple Random Sampling or Random Sampling
The simplest and most common method of sampling is simple random sampling. In simple random sampling, the sample is drawn in such a way that each element or unit of the population has an equal and independent chance of being included in the sample. If a sample is drawn by this method, then it is known as a simple random sample or random sample
Simple Random Sampling without Replacement (SRSWOR)
In simple random sampling, if the elements or units are selected or drawn one by one in such a way that an element or unit drawn at a time is not replaced back to the population before the subsequent draws is called SRSWOR.
Suppose we draw a sample from a population, the size of sample is n and the size of population is N, then total number of possible sample is 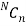
Simple Random Sampling with Replacement (SRSWR)
In simple random sampling, if the elements or units are selected or drawn one by one in such a way that a unit drawn at a time is replaced back to the population before the subsequent draw is called SRSWR.
Suppose we draw a sample from a population, the size of sample is n and the size of population is N, then total number of possible sample is 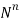 .
.
Parameter-
A parameter is a function of population values which is used to represent the certain characteristic of the population. For example, population mean, population variance, population coefficient of variation, population correlation coefficient, etc. are all parameters. Population parameter mean usually denoted by μ and population variance denoted by 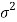
Sample mean and sample variance-
Let 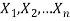 be a random sample of size n taken from a population whose pmf or pdf function f (x,
be a random sample of size n taken from a population whose pmf or pdf function f (x, 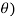
Then the sample mean is defined by-
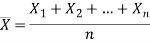
And sample variance-
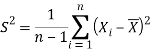
Statistic-
Any quantity which does not contain any unknown parameter and calculated from sample values is known as statistic.
Suppose 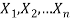 is a random sample of size n taken from a population with mean μ and variance
is a random sample of size n taken from a population with mean μ and variance 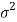 then the sample mean-
then the sample mean-
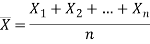
Is a statistic.
Estimator and estimate-
If a statistic is used to estimate an unknown population parameter, then it is known as estimator and the value of the estimator based on observed value of the sample is known as estimate of parameter.
Standard error-
The standard deviation of the sampling distribution is known as standard error.
When we increase the sample size then standard increases.
It plays an important role in large sample theory.
Note- The reciprocal of the standard error is called ‘precision’.
If the size of the sample is less than 30, it is considered as small sample otherwise it is called large sample.
The sampling distribution of large samples is assumed to be normal.
Testing of hypothesis
Hypothesis-
A hypothesis is a statement or a claim or an assumption about the value of a population parameter.
Similarly, in case of two or more populations a hypothesis is comparative statement or a claim or an assumption about the values of population parameters.
For example-
If a customer of a car wants to test whether the claim of car of a certain brand gives the average of 30km/hr is true or false.
Simple and composite hypotheses-
If a hypothesis specifies only one value or exact value of the population parameter then it is known as simple hypothesis. And if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.
Null and alternative hypothesis
The hypothesis which is to be tested as called the null hypothesis.
The hypothesis which complements to the null hypothesis is called alternative hypothesis.
In the example of car, the claim is 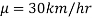 and its complement is
and its complement is 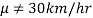 .
.
The null and alternative hypothesis can be formulated as-
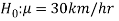
And
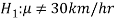
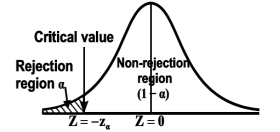
Critical region-
Let 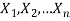 be a random sample drawn from a population having unknown population parameter
be a random sample drawn from a population having unknown population parameter 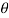 .
.
The collection of all possible values of 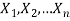 is called sample space and a particular value represent a point in that space.
is called sample space and a particular value represent a point in that space.
In order to test a hypothesis, the entire sample space is partitioned into two disjoint sub-spaces, say, 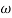 and S –
and S – 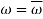 . If calculated value of the test statistic lies in, then we reject the null hypothesis and if it lies in
. If calculated value of the test statistic lies in, then we reject the null hypothesis and if it lies in 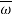 then we do not reject the null hypothesis. The region is called a “rejection region or critical region” and the region
then we do not reject the null hypothesis. The region is called a “rejection region or critical region” and the region 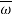 is called a “non-rejection region”.
is called a “non-rejection region”.
Therefore, we can say that
“A region in the sample space in which if the calculated value of the test statistic lies, we reject the null hypothesis then it is called critical region or rejection region.”
The region of rejection is called critical region.
The critical region lies in one or two tails on the probability curve of sampling distribution of the test statistic it depends on the alternative hypothesis.
Therefore, there are three cases-
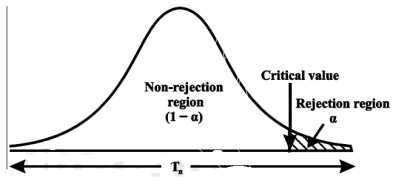
CASE-1: if the alternative hypothesis is right sided such as 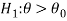 then the entire critical region of size
then the entire critical region of size 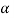 lies on right tail of the probability curve.
lies on right tail of the probability curve.
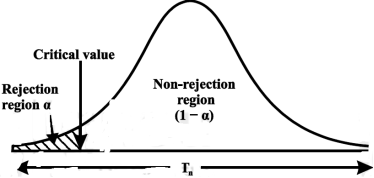
CASE-2: if the alternative hypothesis is left sided such as  then the entire critical region of size
then the entire critical region of size  lies on left tail of the probability curve.
lies on left tail of the probability curve.
CASE-3: if the alternative hypothesis is two sided such as 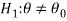 then the entire critical region of size
then the entire critical region of size 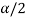 lies on both tail of the probability curve
lies on both tail of the probability curve
Type-1 and Type-2 error-
Type-1 error-
The decision relating to rejection of null hypo. When it is true is called type-1 error.
The probability of type-1 error is called size of the test, it is denoted by 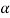 and defined as-
and defined as-
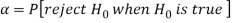
Note-
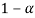 is the probability of correct decision.
is the probability of correct decision.
Type-2 error-
The decision relating to non-rejection of null hypo. When it is false is called type-1 error.
It is denoted by 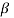 and defined as-
and defined as-
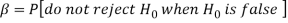
Decision |
 | 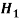 |
Reject 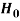 | Type-1 error | Correct decision |
Do not reject 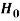 | Correct decision | Type-2 error |
One tailed and two tailed tests-
A test of testing the null hypothesis is said to be two-tailed test if the alternative hypothesis is two-tailed whereas if the alternative hypothesis is one-tailed then a test of testing the null hypothesis is said to be one-tailed test.
For example, if our null and alternative hypothesis are-
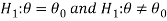
Then the test for testing the null hypothesis is two-tailed test because the
Alternative hypothesis is two-tailed.
If the null and alternative hypotheses are-
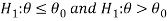
Then the test for testing the null hypothesis is right-tailed test because the alternative hypothesis is right-tailed.
Similarly, if the null and alternative hypotheses are-
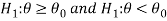
Then the test for testing the null hypothesis is left-tailed test because the alternative hypothesis is left-tailed
Procedure for testing a hypothesis-
Step-1: first we set up null hypothesis 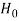 and alternative hypothesis
and alternative hypothesis 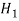 .
.
Step-2: after setting the null and alternative hypothesis, we establish a
Criteria for rejection or non-rejection of null hypothesis, that is,
Decide the level of significance (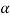 ), at which we want to test our
), at which we want to test our
Hypothesis. Generally, it is taken as 5% or 1% (α = 0.05 or 0.01).
Step-3: The third step is to choose an appropriate test statistic under H0 for
Testing the null hypothesis as given below
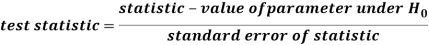
Now after doing this, specify the sampling distribution of the test statistic preferably in the standard form like Z (standard normal), 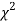 , t, F or any other well-known in literature
, t, F or any other well-known in literature
Step-4: Calculate the value of the test statistic described in Step III on the basis of observed sample observations.
Step-5: Obtain the critical (or cut-off) value(s) in the sampling distribution of the test statistic and construct rejection (critical) region of size 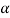 .
.
Generally, critical values for various levels of significance are putted in the form of a table for various standard sampling distributions of test statistic such as Z-table, 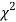 -table, t-table, etc
-table, t-table, etc
Step-6: After that, compare the calculated value of test statistic obtained from Step IV, with the critical value(s) obtained in Step V and locates the position of the calculated test statistic, that is, it lies in rejection region or non-rejection region.
Step-7: in testing the hypothesis we have to reach at a conclusion, it is performed as below-
First- If calculated value of test statistic lies in rejection region at 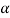 level of significance, then we reject null hypothesis. It means that the sample data provide us sufficient evidence against the null hypothesis and there is a significant difference between hypothesized value and observed value of the parameter
level of significance, then we reject null hypothesis. It means that the sample data provide us sufficient evidence against the null hypothesis and there is a significant difference between hypothesized value and observed value of the parameter
Second- If calculated value of test statistic lies in non-rejection region at 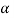 level of significance, then we do not reject null hypothesis. Its means that the sample data fails to provide us sufficient evidence against the null hypothesis and the difference between hypothesized value and observed value of the parameter due to fluctuation of sample
level of significance, then we do not reject null hypothesis. Its means that the sample data fails to provide us sufficient evidence against the null hypothesis and the difference between hypothesized value and observed value of the parameter due to fluctuation of sample
Procedure of testing of hypothesis for large samples-
The sample size more than 30 is considered as large sample size. So that for large samples, we follow the following procedure to test the hypothesis.
Step-1: first we set up the null and alternative hypothesis.
Step-2: After setting the null and alternative hypotheses, we have to choose level of significance. Generally, it is taken as 5% or 1% (α = 0.05 or 0.01). And accordingly, rejection and non-rejection regions will be decided.
Step-3: Third step is to determine an appropriate test statistic, say, Z in case of large samples. Suppose Tn is the sample statistic such as sample
Mean, sample proportion, sample variance, etc. for the parameter 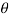
Then for testing the null hypothesis, test statistic is given by
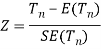
Step-4: the test statistic Z will be assumed to be approximately normally distributed with mean 0 and variance 1 as
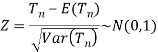
By putting the values in above formula, we calculate test statistic Z.
Suppose z be the calculated value of Z statistic
Step-5: After that, we obtain the critical (cut-off or tabulated) value(s) in the sampling distribution of the test statistic Z corresponding to 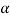 assumed in Step II. We construct rejection (critical) region of size α in the probability curve of the sampling distribution of test statistic Z.
assumed in Step II. We construct rejection (critical) region of size α in the probability curve of the sampling distribution of test statistic Z.
Step-6: Take the decision about the null hypothesis based on the calculated and critical values of test statistic obtained in Step IV and Step V.
Since critical value depends upon the nature of the test that it is one tailed test or two-tailed test so following cases arise-
Case-1 one-tailed test- when 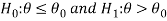 (right-tailed test)
(right-tailed test)
In this case, the rejection (critical) region falls under the right tail of the probability curve of the sampling distribution of test statistic Z.
Suppose 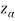 is the critical value at
is the critical value at 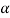 level of significance so entire region greater than or equal to
level of significance so entire region greater than or equal to 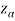 is the rejection region and less than
is the rejection region and less than
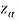 is the non-rejection region
is the non-rejection region
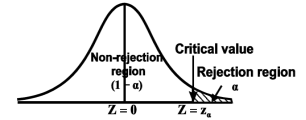
If z (calculated value) ≥ 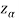 (tabulated value), that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
(tabulated value), that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at 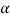 level of significance. Therefore, we conclude that sample data provides us sufficient evidence against the null hypothesis and there is a significant difference between hypothesized or specified value and observed value of the parameter.
level of significance. Therefore, we conclude that sample data provides us sufficient evidence against the null hypothesis and there is a significant difference between hypothesized or specified value and observed value of the parameter.
If z <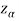 that means the calculated value of test statistic Z lies in non-rejection region, then we do not reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in non-rejection region, then we do not reject the null hypothesis H0 at 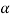 level of significance. Therefore, we conclude that the sample data fails to provide us sufficient evidence against the null hypothesis and the difference between hypothesized value and observed value of the parameter due to fluctuation of sample.
level of significance. Therefore, we conclude that the sample data fails to provide us sufficient evidence against the null hypothesis and the difference between hypothesized value and observed value of the parameter due to fluctuation of sample.
So, the population parameter 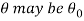
Case-2: when 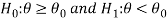 (left-tailed test)
(left-tailed test)
The rejection (critical) region falls under the left tail of the probability curve of the sampling distribution of test statistic Z.
Suppose -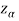 is the critical value at
is the critical value at 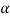 level of significance then entire region less than or equal to -
level of significance then entire region less than or equal to -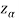 is the rejection region and greater than -
is the rejection region and greater than -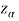 is the non-rejection region
is the non-rejection region
If z ≤-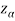 , that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
, that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at 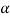 level of significance.
level of significance.
If z >-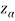 , that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at
, that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at 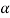 level of significance.
level of significance.
In case of two tailed test-
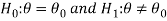
In this case, the rejection region falls under both tails of the probability curve of sampling distribution of the test statistic Z. Half the area (α) i.e., α/2 will lie under left tail and other half under the right tail. Suppose 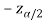 and
and 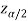 are the two critical values at the left-tailed and right-tailed respectively. Therefore, entire region less than or equal to
are the two critical values at the left-tailed and right-tailed respectively. Therefore, entire region less than or equal to 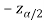 and greater than or equal to
and greater than or equal to 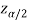 are the rejection regions and between -
are the rejection regions and between -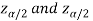 is the non-rejection region.
is the non-rejection region.
If Z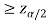 that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at 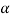 level of significance.
level of significance.
If 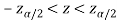 that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at 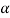 level of significance.
level of significance.
Testing of hypothesis for population mean using Z-Test
For testing the null hypothesis, the test statistic Z is given as-
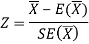
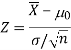
The sampling distribution of the test statistics depends upon variance 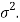
So that there are two cases-
Case-1: when 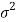 is known -
is known -
The test statistic follows the normal distribution with mean 0 and variance unity when the sample size is the large as the population under study is normal or non-normal. If the sample size is small then test statistic Z follows the normal distribution only when population under study is normal. Thus,
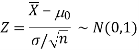
Case-1: when 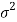 is unknown –
is unknown –
We estimate the value of 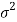 by using the value of sample variance
by using the value of sample variance
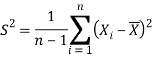
Then the test statistic becomes-
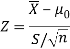
After that, we calculate the value of test statistic as may be the case (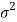 is known or unknown) and compare it with the critical value at prefixed level of significance α.
is known or unknown) and compare it with the critical value at prefixed level of significance α.
Example: A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
Sol.
It is given that-
Specified value of population mean = 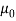 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
The null and alternative hypothesis will be-
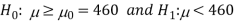
Also, the alternative hypothesis left-tailed so that the test is left tailed test.
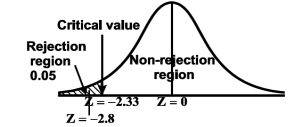
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So, we should use t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by
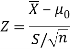
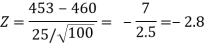
We get the critical value of left tailed Z test at 1% level of significance is 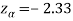
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Example: A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?
Sol.
Here we have-
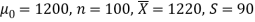
The company may accept the new CFL light when average life of
CFL light is greater than 1200 hours. So, the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So, our claim is 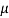 > 1200 and its complement is
> 1200 and its complement is 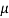 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
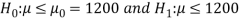
Since the alternative hypothesis is right-tailed so the test is right-tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.
Therefore, test statistic is given by
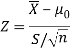
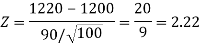
The critical values for right-tailed test at 5% level of significance is
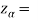 1.645
1.645
Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e., we support our claim at 5% level of significance
Thus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Significance test of difference between sample means
Given two independent examples 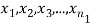 and
and 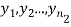 with means
with means 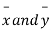 standard derivations
standard derivations 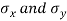 from a normal population with the same variance, we have to test the hypothesis that the population means
from a normal population with the same variance, we have to test the hypothesis that the population means 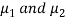 are same For this, we calculate
are same For this, we calculate
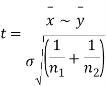
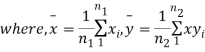
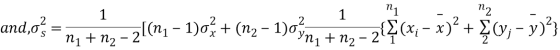
It can be shown that the variate t defined by (1) follows the t distribution with 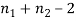 degrees of freedom.
degrees of freedom.
If the calculated value 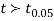 the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If 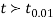 , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 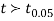 the data is said to be consistent with the hypothesis that
the data is said to be consistent with the hypothesis that 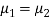 .
.
Cor. If the two samples are of same size and the data are paired, then t is defined by
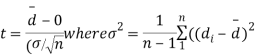
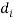 =difference of the ith member of the sample
=difference of the ith member of the sample
d=mean of the differences =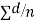 and the member of d.f.=n-1.
and the member of d.f.=n-1.
Example
Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Sol. We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
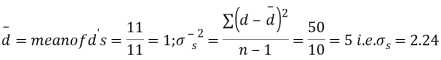
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.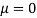
Then, 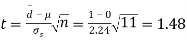 nearly and df v=11-1=10
nearly and df v=11-1=10
Students | 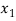 | 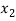 | 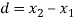 | 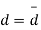 | 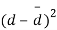 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| 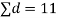 |
| 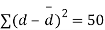 |
We find that 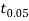 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 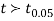 , the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefitted by extra coaching.
Example:
From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight?
Sol. We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
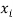 | 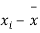 | 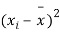 | 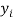 | 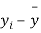 | 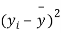 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |
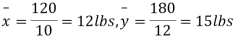
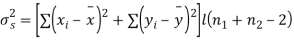
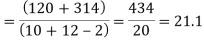
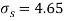
Assuming that the samples do not differ in weight so far as the two diets are concerned i.e., 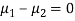
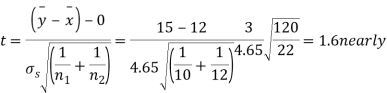
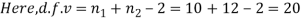
For v=20, we find 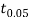 =2.09
=2.09
The calculated value of 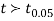
Hence the difference between the samples means is not significant i.e., thew two diets do not differ significantly as regards their effects on increase in weight.
Testing of hypothesis for difference of two population means using Z-Test-
Let there be two populations, say, population-I and population-II under study.
Also let 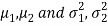 denote the means and variances of population-I and population-II respectively where both
denote the means and variances of population-I and population-II respectively where both 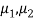 are unknown but
are unknown but 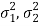 may be known or unknown. We will consider all possible cases here. For testing the hypothesis about the difference of two population means, we draw a random sample of large size n1 from population-I and a random sample of large size n2 from population-II. Let
may be known or unknown. We will consider all possible cases here. For testing the hypothesis about the difference of two population means, we draw a random sample of large size n1 from population-I and a random sample of large size n2 from population-II. Let 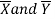 be the means of the samples selected from population-I and II respectively.
be the means of the samples selected from population-I and II respectively.
These two populations may or may not be normal but according to the central limit theorem, the sampling distribution of difference of two large sample means asymptotically normally distributed with mean 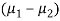 and variance
and variance 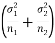
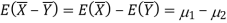
And
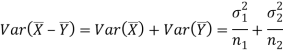
We know that the standard error = 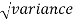
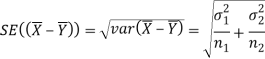
Here, we want to test the hypothesis about the difference of two population means so we can take the null hypothesis as
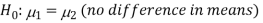
Or
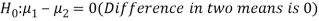
And the alternative hypothesis is-
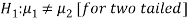
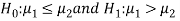
Or
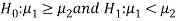
The test statistic Z is given by-
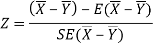
Or
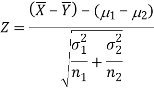
Since under null hypothesis we assume that 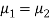 , therefore, we get-
, therefore, we get-
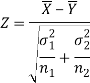
Now, the sampling distribution of the test statistic depends upon 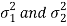 that both are known or unknown. Therefore, four cases arise-
that both are known or unknown. Therefore, four cases arise-
Case-1: When 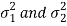 are known and
are known and 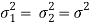
In this case, the test statistic follows normal distribution with mean
0 and variance unity when the sample sizes are large as both the populations under study are normal or non-normal. But when sample sizes are small then test statistic Z follows normal distribution only when populations under study are normal, that is,
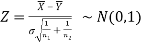
Case-2: When 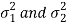 are known and
are known and 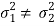
In this case, the test statistic also follows the normal distribution as described in case I, that is,
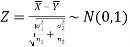
Case-3: When 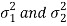 are unknown and
are unknown and 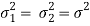
In this case, σ2 is estimated by value of pooled sample variance 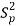
Where,
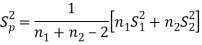
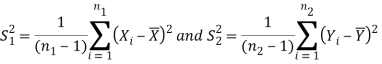
And test statistic follows t-distribution with (n1 + n2 − 2) degrees of freedom as the sample sizes are large or small provided populations under study follow normal distribution.
But when the populations are under study are not normal and sample sizes n1 and n2are large (> 30) then by central limit theorem, test statistic approximately normally distributed with mean
0 and variance unity, that is,
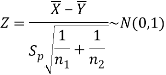
Case-4: When 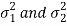 are unknown and
are unknown and 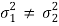
In this case, 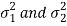 are estimated by the values of the sample variances
are estimated by the values of the sample variances 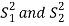 respectively and the exact distribution of test statistic is difficult to derive. But when sample sizes n1 and n2 are large (> 30) then central limit theorem, the test statistic approximately normally distributed with mean 0 and variance unity,
respectively and the exact distribution of test statistic is difficult to derive. But when sample sizes n1 and n2 are large (> 30) then central limit theorem, the test statistic approximately normally distributed with mean 0 and variance unity,
That is,
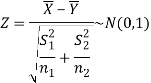
After that, we calculate the value of test statistic and compare it with the critical value at prefixed level of significance α.
Example: A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face-to-face mode yields examination results mean and SD respectively as-
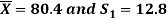
And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:
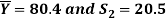
Are both educational methods statistically equal at 5% level?
Sol. Here we have-
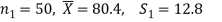
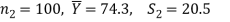
Here we wish to test that both educational methods are statistically equal. If 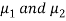 denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is 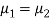 and its complement is
and its complement is 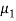 ≠
≠ 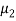 . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
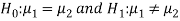
Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So, we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by
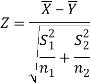
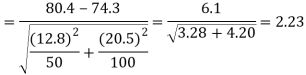
The critical (tabulated) values for two-tailed test at 5% level of significance are-
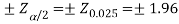
Since calculated value of Z (= 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
Reject the null hypothesis i.e., we reject the claim at 5% level of significance
Level of significance-
The probability of type-1 error is called level of significance of a test. It is also called the size of the test or size of the critical region. Denoted by 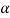 .
.
Basically, it is prefixed as 5% or 1% level of significance.
If the calculated value of the test statistics lies in the critical region, then we reject the null hypothesis.
The level of significance relates to the trueness of the conclusion. If null hypothesis does not reject at level 5% then a person will be sure “concluding about the null hypothesis” is true with 95% assurance but even it may false with 5% chance.
Student’s t distribution
General procedure of t-test for testing hypothesis-
Let X1, X2,…, Xn be a random sample of small size n (< 30) selected from a normal population, having parameter of interest, say,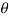
Which is actually unknown but its hypothetical value- then
Step-1: First of all, we setup null and alternative hypotheses
Step-2: After setting the null and alternative hypotheses our next step is to decide a criteria for rejection or non-rejection of null hypothesis i.e., decide the level of significance 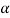 at which we want to test our null hypothesis. We generally take
at which we want to test our null hypothesis. We generally take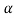 = 5 % or 1%.
= 5 % or 1%.
Step-3: The third step is to determine an appropriate test statistic, say, t for testing the null hypothesis. Suppose Tn is the sample statistic (may be sample mean, sample correlation coefficient, etc. depending upon 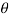 ) for the parameter
) for the parameter 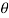 then test-statistic t is given by
then test-statistic t is given by
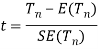
Step-4: As we know, t-test is based on t-distribution and t-distribution is described with the help of its degrees of freedom, therefore, test statistic t follows t-distribution with specified degrees of freedom as the case may be.
By putting the values of Tn, E(Tn) and SE(Tn) in above formula, we calculate the value of test statistic t. Let t-cal be the calculated value of test statistic t after putting these values.
Step-5: After that, we obtain the critical (cut-off or tabulated) value(s) in the sampling distribution of the test statistic t corresponding to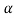 assumed in Step II. The critical values for t-test are corresponding to different level of significance (α). After that, we construct rejection (critical) region of size
assumed in Step II. The critical values for t-test are corresponding to different level of significance (α). After that, we construct rejection (critical) region of size 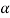 in the probability curve of the sampling distribution of test statistic t.
in the probability curve of the sampling distribution of test statistic t.
Step-6: Take the decision about the null hypothesis based on calculated and critical value(s) of test statistic obtained in Step IV and Step V respectively.
Critical values depend upon the nature of test.
The following cases arises-
In case of one tailed test-
Case-1: 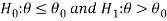 [Right-tailed test]
[Right-tailed test]
In this case, the rejection (critical) region falls under the right tail of the probability curve of the sampling distribution of test statistic t.
Suppose 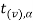 is the critical value at
is the critical value at 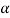 level of significance then entire region greater than or equal to
level of significance then entire region greater than or equal to 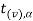 is the rejection region and less than
is the rejection region and less than 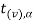 is the non-rejection region.
is the non-rejection region.
If 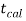 ≥
≥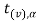 that means calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis
that means calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis 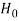 at
at 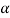 level of significance.
level of significance.
If 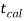 <
<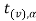 that means calculated value of test statistic t lies in non-rejection region, then we do not reject the null hypothesis
that means calculated value of test statistic t lies in non-rejection region, then we do not reject the null hypothesis 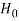 at
at 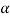 level of significance.
level of significance.
Case-2: 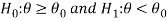 [Left-tailed test]
[Left-tailed test]
In this case, the rejection (critical) region falls under the left tail of the probability curve of the sampling distribution of test statistic t.
Suppose -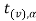 is the critical value at
is the critical value at 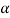 level of significance then entire region less than or equal to -
level of significance then entire region less than or equal to -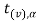 is the rejection region and greater than -
is the rejection region and greater than -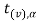 is the non-rejection region.
is the non-rejection region.
If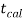 ≤ −
≤ −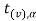 that means calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis
that means calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis 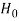 at
at 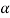 level of significance.
level of significance.
If 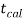 > −
> −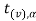 , that means calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis
, that means calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis 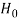 at
at 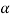 level of significance.
level of significance.
In case of two tailed test-
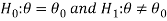
In this case, the rejection region falls under both tails of the probability curve of sampling distribution of the test statistic t. Half the area (α) i.e., α/2 will lie under left tail and other half under the right tail. Suppose -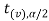 , and
, and 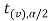 are the two critical values at the left- tailed and right-tailed respectively. Therefore, entire region less than or equal to -
are the two critical values at the left- tailed and right-tailed respectively. Therefore, entire region less than or equal to -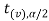 and greater than or equal to
and greater than or equal to 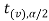 are the rejection regions and between -
are the rejection regions and between -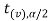 and
and 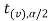 is the non-rejection region.
is the non-rejection region.
If 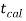 ≥
≥ 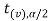 or
or 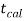 ≤ -
≤ -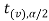 , that means calculated value of test statistic t lies in the rejection(critical) region, then we reject the null hypothesis
, that means calculated value of test statistic t lies in the rejection(critical) region, then we reject the null hypothesis 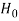 at
at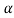 level of significance.
level of significance.
And if -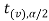 <
< 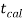 <
< 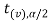 , that means calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis
, that means calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis 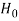 at
at 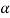 level of significance.
level of significance.
Testing of hypothesis for population mean using t-Test
There are the following assumptions of the t-test-
- Sample observations are random and independent.
- Population variance
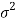 is unknown
is unknown - The characteristic under study follows normal distribution.
For testing the null hypothesis, the test statistic t is given by-
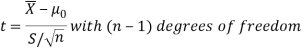
Example: A tube manufacturer claims that the average life of a particular category of his tube is 18000 km when used under normal driving conditions. A random sample of 16 tube was tested. The mean and SD of life of the tube in the sample were 20000 km and 6000 km respectively.
Assuming that the life of the tube is normally distributed, test the claim of the manufacturer at 1% level of significance using appropriate test.
Sol.
Here we have-
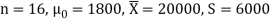
We want to test that manufacturer’s claim is true that the average life (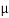 ) of tube is 18000 km. So, claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
) of tube is 18000 km. So, claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
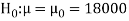
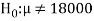
Here, population SD is unknown and population under study is given to be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-
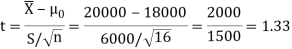
The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 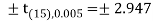
Since calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater that critical value (= − 2.947), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis. We conclude that sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
Key takeaways-
- Type-1 error-
The decision relating to rejection of null hypo. When it is true is called type-1 error.
The probability of type-1 error is called size of the test, it is denoted by 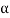 and defined as-
and defined as-
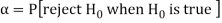
Note-
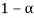 is the probability of correct decision.
is the probability of correct decision.
2. Type-2 error-
The decision relating to non-rejection of null hypo. When it is false is called type-1 error.
It is denoted by 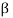 and defined as-
and defined as-

3. 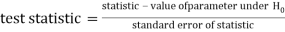
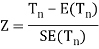
4. For testing the null hypothesis, the test statistic Z is given as-
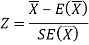
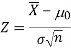
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- IGNOU
- Fundamentals of mathematical statistics by SC Gupta and VK kapoor