Unit - 4
Retaining Wall
Retaining structures are engineered to retain soil or rock from an area, building or any type of structure. The main functions of retaining structure are to stabilize hillsides and control erosion.
Several types of retaining structures are as follows
1. Gravity walls
2. Cantilever wall
3. Sheet pile wall
4. Anchored earth retaining wall
5. Mechanically stabilized earth wall. i.e., Reinforced concrete retaining wall.
Retaining wall is a structure which is constructed to retain the earth, coal, water etc.
Retaining walls are mainly provided in construction of roads, embankments bridge abutments, basement in building etc.
The material which is retained by the retraining wall is called as backfill. The slopping backfill is called as inclined surcharge.
The term surcharge means the rock fill above the level of the top of the wall.
The backfill exerts a push or lateral pressure on the retain ng wall which tries to overturn bends and slide the retaining wall.
Retaining walls should be designed to resist the lateral earth pressure from the sides and the soil pressure acting vertically on the footing slab integrally built with the vertical slab.
Functions and types of retaining walls
Types of Retaining Walls
Retaining walls are classified according to the shape and mode of resisting the pressure of backfills.
Following are the common types of retaining walls.
1. Gravity retaining wall.
2. Cantilever retaining wall.
3. Counter fort retaining wall.
4. Buttress retaining wall.
1. Gravity Retaining Wall
A gravity retaining wall in which the weight of the retaining wall provides stability against the pressure exerted by the backfill
It is made up of stone masonry or plain cement concrete. The principle of design of gravity retaining wall is that tension is not developed anywhere in the section. Therefore, it is designed by using "Middle Third Rule".
2. Cantilever Retaining Wall
The most common and widely used retaining wall is of the cantilever type. Vertical stem resisting earth pressure from one side and the slab bends like a cantilever
Depending upon the soil pressure the thickness of stem slab varies. i.e., larger at bottom and gradually decreased towards top.
The bottom slab is called as toe slab and heel slab both of them act as a horizontal cantilever
A cantilever type of retaining walls are adopted for small to medium height up to 6 m
The stem heel and toe all resist the earth pressure by bending. These walls can be L or inverted T shaped. The weight of the earth on the heel slab and the weight of the retaining wall together provided stability to the wall.
3. Counter fort retaining wall
For height more than 5 m of earth fill the bending moment developed in stem heel and toe slab are very large.
Resulting in larger thickness of structural of structural element and turns to uneconomical section. Hence in this case counter fort type retaining walls are adopted.
Following fig shows a typical counter retaining wall consisting of a stem toe slab heel slab and counter forts.
4. Buttress retaining wall
It is similar to the counter fort retaining wall but with the difference that in buttress retaining wall the counter fort called as buttress are provided on the opposite side of the backfill
It is economical and buttress are design as a compression member but still not preferred buttresses are visible and they occupy the space in front of the wall.
Weep holes are provided to draining the rain water from backfill
Structural behaviour of retaining wall
The retaining wall is a structure that is constructed and constructed to withstand the back pressure of the ground, where there is a desired change in ground height that exceeds the resting angle of the soil
- Gravity wall, cantilever retaining wall, sheet pile retaining wall, bored pile retaining wall, anchored retaining wall are the types of retaining wall are often the types of retaining wall are the types of retaining walls are commonly used.
- Strong storage walls that do not allow to be made are often made as gravity walls. These walls are large in size. However, large gravitational walls may not be operational due to economic and spatial constraints.
- Also, in some cases, adequate pouring of solid cantilever walls can be allowed due to site constraints, and these walls need to be built with higher ground pressures, rather than active ground pressures. One way to deal with these issues is to reduce the focus from the wall.
- There are many ways to reduce the pressure on the ground, such as using a small weight gain. An effort has been made to understand the function of the cantilever wall with auxiliary shelves and therefore to evaluate the performance of the shelves to reduce ground pressure and bending time on the wall.
- The pressure relief shelf is a small cantilever platform with a limited width, extending to the rear angles at right angles, throughout the length of the retaining wall, monolithically constructed with a retaining wall stem.
- The use of an aid shelf not only reduces the pressure on the outside world but also provides economic stability and increases overall stability.
- Klein provides two separate ground pressure distributions namely the non-expanded shelf in the split line (short shelf) and the extended shelf in the split line (long shelf).
- The parameters affecting the structure of a cantilever wall with shelves are the number of shelves, the shape of the shelves and the width of the shelves.
- This paper introduces a parametric study of these factors affecting the construction of a wall using shelves. An effort is being made to find the best shelf space and the right width of shelves by looking at the effect of a short shelf and a long shelf.
- The differences between the base pressure (Pmax) and the minimum pressure (Pmin) in the base are also investigated.
Key takeaways:
Retaining structures are engineered to retain soil or rock from an area, building or any type of structure. The main functions of retaining structure are to stabilize hillsides and control erosion.
The various force acting on retaining wall are shown in fig.
- Self-weight of stem, Toe slab and Heel slab (W4, W2, W3 respectively)
- Upward soil pressure
- Weight of backfill
- Horizontal and vertical earth pressure components
Hence above force is acting on the retaining walls.
The general relation for the coefficient for the coefficient of active earth pressure based on Rankine’s theory is given by the relation.
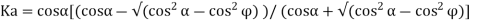
But for level backfill 
Ka = 1-sin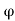 / 1+sin
/ 1+sin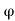
And
Kp 1+sin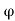 / 1-sin
/ 1-sin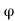
Where Ka and Kp are coefficient of active and passive earth pressure respectively.
5. Earth pressure for different backfill condition of soil
- Dry or moist soil
- Submerged soil
- Partly submerged soil
- Layered soil
- Uniform surcharge soil
- Inclined backfill
- Backfill is horizontal with uniform surcharge w/m at a distance a from stem.
Key takeaways:
- Dry or moist soil
- Submerged soil
- Partly submerged soil
- Layered soil
Stability of retaining wall against overturning and sliding
Overturning is one of the limitations of wall stability. In order to improve this post-rear-force analysis it must be tested against the surface of the allocated surface called the thrust surface, usually on the gravitational wall behind the wall, and on cantilever walls it is considered to be a vertical plane
Although Danilevsky (1982) examined the problem in terms of common terms, the stability of anti-displacement walls has been positively assessed by the safety type F, which is defined as the ratio between the resistance times and the number of turning times relative to the toe. So, with the simple cases of Fig. 1, the security item is provided by
F = Wx / Sa d
Where W = the weight of the wall and the soil between the wall and the focus area; Sa = active focus; and x and d = their arms, respectively.
Calculations are usually made using straight and vertical parts of the S, (called Sa and S, respectively). For this purpose, the upper part of the active focus can be considered in two different ways: such as reducing the moment of overturning
F = Wx / Sah ys – Sav X's
Or increasing the resisting moment
F = W x + S a v x s / S a h ys
Where y s and X's = arms of S a h and S a v respectively. Both of these formulas are used in the analysis of wall durability
(Huntington 1957). However, they are fundamentally different. The value of the security feature provided by (3) remains a positive number, and that (2) may divert or subtract negative numbers. Moreover, only (2) is the direct result of (1), while (3) corresponds to the incorrect change of one term from denominator to number.
The design of retaining wall should confirm to the stability requirement specified in IS 456:2000 which includes overturning and sliding
The factor of safety against overturning and sliding should be not less than 1.4
- Overturning
The overturning wall overturns with the toe as the center of rotation
FS (Overturning)= Total restoring moments/Total overturning Moments > 1.55
2. Sliding
The resistance developed against sliding of the retaining wall is mainly due to the frictional force generated between the base slab and supporting soil expressed as,
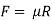
Where
R= Resultant soil pressure acting on the base slab
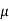 = Coefficient of friction between concrete and soil
= Coefficient of friction between concrete and soil
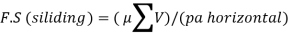
3. Shear key
In case of backfill with discharge the active pressure is relatively high and required factor of safety against sliding by frictional force will not be sufficient.
In such a case it is advantages to provide a shear key projecting below the slab as shown in fig.
Key takeaways:
Overturning is one of the limitations of wall stability. In order to improve this post-rear-force analysis it must be tested against the surface of the allocated surface called the thrust surface, usually on the gravitational wall behind the wall, and on cantilever walls it is considered to be a vertical plane
Design of cantilever retaining wall by Limit State Method
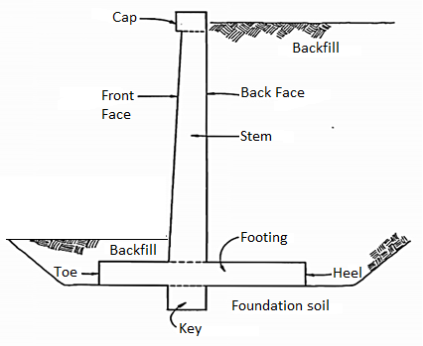
Fig: Cantilever retaining wall
Main Features -
- Calculate the coefficients of global pressure based on Rankine's theory and Coulomb's theory.
- Calculate the force of gravity on the side that works on the wall.
- Wall analysis to test various conditions of durability and calculate safety Factor
- Calculate the horizontal coefficients according to India's standard code IS: 1893.
- Calculate the coefficients of seismic pressure according to IS: 1893, cl. 8.1.
- Perform soil analysis using a simulated method of analyzing soil pressure.
- Design of reinforcement of various wall materials.
Assumption
- The granular regression is considered analysis, meaning that there is no cohesion in the regression soil.
- Appropriate pipes are considered to be provided by the designer so that no hydrostatic pressure is built up behind the wall.
- It is assumed that the distribution of the triangular pressure is formed behind the wall due to the filled earth.
- All ground pressure winds are considered to operate on a vertical plane, passing behind the base of the base slab.
- The inclination of the wall and the friction angle between the wall and the reverse, it is assumed that there is no zero in this
Design Parameters:
Height of earth to be retained, h (m)
Surcharge pressure on backfill, W s (kN/m2)
Soil Properties: ...
Angle of internal friction of soil, φ (°)
Slope of backfill, β (°) with the horizontal.
Unit weight of soil, in kN/m2
Soil-wall interface friction, δ (°)
Concrete density, in kN/m2
Proportioning of retaining wall and design approach
- Width of base slab(b)
Assume the width of base slab is in between
b = 0.5 H to 0.6 h for walls without surcharge
b = 0.6 H to 0.8 H for surcharge walls
Where H = Total height of retaining walls
b. Thickness of base slab
Assume thickness of slab in between H/14 to H/12
c. Thickness of stem at top is 200mm
d. Design approach
The stem heel and toe slab structurally behave as cantilever slabs and deforms as shown in fig. Hence the critical section XX XY ZZ are consider for design
Procedure:
- Design constants and coefficient of active earth pressure
Xu max = 0.46-Fe500
= 0.48-Fe415
= 0.53 –Fe 250
Ru max = 0.133 Fck -Fe500
= 0.138 Fck -Fe415
= 0.148 Fck –Fe 250
Coefficient of earth pressure
Ka = 1- Sin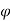 /1+Sin
/1+Sin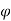
2. Preliminary dimensions
Using pressure diagram find Mu = Pa. H/3
Depth at bottom for stem = 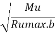
3. Determine horizontal pressure acting on retaining wall by using condition of backfill given
4. Determine self-weight of wall and soil on the heel slab
Where W1 W2 W3 and W4 are the weight of walls and soil on heel slab
X1, x2 X3 and X4 are the distance of centroid from 0
5. Check of retaining wall against
1) Overturning
2) Sliding
3) Bearing pressure
- Check for overturning
Find stabilizing/restoring moment developed due to self-weight and soil on the heel slab.
Ms = W1x1+W2x2+W3x3+W4x4
Overturning moment developed due to earth pressure based on backfill condition.
Factor of safety for overturning = Stabilizing moment /Overturning moment >1.55
2. Check for sliding
Factor of safety for sliding = 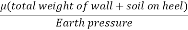
If factor of safety against sliding less than 1.55 then a shear key may be provided as shown in fig. This shear key increases the resistance against sliding as the passive earth pressure developed on the shear key provides additional resistance against sliding.
3. Design of shear key
- The wall should be safe for lateral pressure of 1.55 P
- Find maximum available friction =
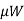
- Find unbalanced horizontal force = 1.55P-
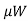
- Find depth of shear key y
Let y be the height of the key
Safe bearing strength of soil for
Horizontal loading = 0.7 x SBC of soil
e. Total moment = unbalanced moment x y
By using this moment design the reinforcement for shear key
F. Base width of slab
B/H = (0.75 Ka)/(1-K)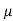
4. Check for Bearing pressure
Net moment = stabilizing moment – Overturning moment
Resultant of weight and earth pressure should i.e., in middle third of the base so that no tension will be developed.
Position of resultant (x) = net moment/Pa
Eccentricity e= h/2 –x
If e positive the pmax is below the toe and p min is below the toe.
If e is negative the P max is below the heel and P max is below the toe.
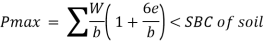
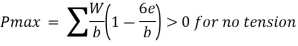
Step 6 Design of toe slab
Moment of x-x = moment due to earth pressure – moment due to self-weight of beam
Design of toe is same as slab design. Tension develops on bottom side so main steel in toe slab is at bottom side.
Step 7 Design of heel slab
Moment at X-x = + moment due to self-weight of slab+ moment due to soil on the heel slab- moment due to earth pressure
Design of heel slab is also same as slab design. Tension developed at top side so main steel in heel slab is at top side.
Step 8 Design of stem
To determine steel reinforcement moment due to earth pressure at the bottom of stem is used. Curtailment of reinforcement plays very important role as earth pressure is lower towards top At 0.79 h from top of the stem half curtailment provided towards top.
Step 9 Detailing
Retaining walls reinforcement details
Examples:
Design RCC retaining wall to retain earthen embankment 4.1 m high above the G.L The embankment is surcharge at an angle 20 degree with embankment unit weight of soil is 18 kN/m^3. Angle of repose is 30, good foundation for wall is available at a depth of 1.1 m below GL permissible SBC of soil is 160 KN/m^2 u= 0.62 M20 concrete and Fe500. Sketch the reinforcement details.
Solution:
Given data:
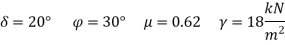
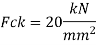
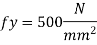
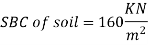
Height of backfill above GL = 4.1 depth of foundation= 1.1 m
Step 1 Calculation of design constant and coefficient of active pressure
X u max = 0.46 Rmax = 0.133 Fck
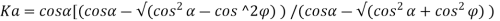
Step 2: Proportioning of retaining wall
- Total height of retaining wall
H= Height of backfill + depth of foundation
H= 4.1+1.1= 5.2 m = 5200 mm
b. Calculation of base width and toe length
B= 0.6 H to 0.8 H = 3.12 to 4.16
Assume b = 4 m = 4000mm
Minimum toe length = 1/3 b = 1.33 m = 1330 mm
c. Thickness of base slab = H/14 to H/12 = 0.4 mm = 400mm
d. Thickness of stem at top = 150 to 200
Assume thickness of stem at top = 200 mm
e. Height of stem
h= H-Thickness of base slab
h = 5200-400 = 4800 mm = 4.8 mm
f. Thickness of stem at base
Total active earth pressure acting on stem Ps = ½ Ka 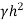
Pa horizontal = 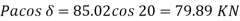
Ps Vertical
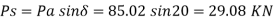
Horizontal components act as distant h/3 from base
Bending moment t the base of stem = Pa horizontal x 1.5
= 79.89 x 1.6 = 127.82 KN.m
Factored BM = 1.5 x 127.82 = 191.73 kN.m
For Fe500
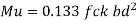
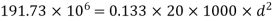
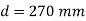
Overall thickness at the base of stem
D= d+C.C+
Assuming clear cover equal to50 mm and using 16 mm 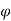 bars
bars
= 270 +50+16/2 = 328 mm
g) Heel height = b-toe length-thickness of stem at bottom
= 4000-1330-328 = 2342 mm= 2.34 m
h) Total active earth pressure considering surcharge
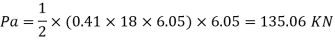
Pa horizontal = 135.06 x cos 20 = 126.91 KN
Acting at H/3 = 6.05/3 = 2.01 m
Pv= 135.06 sin 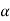 =135.06 x sin 20 = 46.19 KN
=135.06 x sin 20 = 46.19 KN
Step 3 Load calculation
Type of load | Magnitude | Distance from toe lever arm | BM kN. m | Remarks |
A Horizontal load Pa cos 20 | 126.91 | 2.01 | 255.08 | Over turning moment |
B Vertical load |
|
|
|
|
| ½ x 0.128 x 4.8 x 25 = 7.68 KN | = 1.33 +2/3 (0.128) = 1.41 | 10.82 | Restoring moment |
| = 0.2 x 4.8 x25 = 24 kN | = 1.33 +0.128 +0.2 /2 = 1.558 | 37.39 | Restoring moment |
| = 0.4 x 4x15 = 40 | 2.0 | 80 | Restoring moment |
Surcharge |
|
|
|
|
| = ½ (a+b) l = ½ (4.8 +5.65) x 2.35 x18 = 220.07 | = 1.33 +0.328+1.2 = 2.86 | 629.3 | Restoring moment |
PV vertical | 46.19 | 4 | 184.76 | Restoring moment |
Summary
Total horizontal load = 126.91 KN
Total vertical load = 7.68 +24+40+220+46.19 = 338 KN
Total vertical moment = 942.31 KN.m
Total horizontal moment = 255.08 KN
Step 4 Check for stability condition
- Check against overturning moment
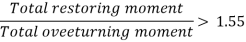
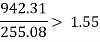
b. Check against sliding
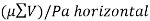 >1.55
>1.55
c. Check against pressure
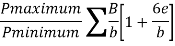
e = b/2 –x = 4/2 -2.03= -0.03 m
d. e < b/6
0.03 <0.06
e. P maximum = 338/4[1+(x0.03)/4)] = 88.30 KN/m^2
P minimum = 338/4 [1-(6x0.03)/4] =80.69 KN/m^2
Step 5 Design of toe slab
Toe Slab is act as cantilever because it’s one end is free and other end is fix.
Forces acts on toe slab
- Self-weight of toe slab
- Upward pressure intensity
Assume unit weight of concrete = 25 KN/m^2
Self-weight of toe slab = Area x 1 x25 = 1.33 x0.4x25= 13.3 KN
Act at 1.33/2 = 0.67 from fixed end.
By similarity of triangle
4/7.61 = 1.33/x
X= 2.53
Upward pressure intensity
0.5 (80.69+83.2) x 1.33= 109 KN
Act as [ {2a+b}/{a+b}] l/3 from fixed end
BM at fixed end = 63.029 KN.m
Mu = 1.5 x63.029 KN
Calculation of Ast =
Ast = 668.75 mm^2
Check for Ast min
For fe 500 Ast min = 0.12%bD
Ast min = 440 mm^< Ast
Spacing = ast /Ast = 300.5 mm
S= 300 mm
Provide 16 mm @ 300 mm c/c at bottom of toe slab and extending all the steel up to heel slab at length equal to development length
Distribution Steel
Provide distribution steel = Ast min = 480 mm^2
S= ast/Ast x 1000
Using 8 mm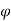
S= 100 mm
Provide 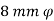 100 mm, perpendicular to main steel.
100 mm, perpendicular to main steel.
Check for shear
Consider a critical section distance d from the fixed end
SF at critical section: 80.65 KN
Pf of steel = -0.195
From table 19 IS 456-2000
By interpolation:
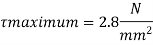
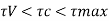
Hence no shear reinforcement is required
Step 6 Design of Heel slab
This member also acts as cantilever
Force act as heel slab
- Self-weight = 23.5 KN
- Weight of backfill = 220.07 KN
- Vertical components = 11.29 KN
Act at 2.35 /2 = 1.18 m
BM= 67.24 KN.m
Ast = 715.84 mm^2 >Ast minimum
S= 280 mm
Provide 16 mm @ 280 mm c/c at top of heel slab. As the tension is on top side.
Distribution Steel
Provide 8 mm @ 100 mm c/c perpendicular to main steel
Check for shear
Consider the critical section at fixed end
SF= 52.62
Factored SF = 78.93 KN
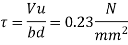
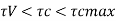
Step 7 Design of stem
Design as a cantilever slab fixed at one end and free at other end
Stem moment = 191. 73 KN
Calculation Ast
Ast min. 393.6 mm^2 <Ast
Spacing S = 135 mm
Ast provide = 1488.59 mm^2
Distribution steel
Provide 8 mm @ 125 mm c/c
Step 8 Detailing
Key takeaways:
Features
Calculate the coefficients of global pressure based on Rankine's theory and Coulomb's theory, force of gravity on the side, reinforcement of various wall materials, Coefficients of seismic pressure.
Case Study:
- Retaining Wall
Retaining walls are classified according to the shape and mode of resisting the pressure of backfills.
Following are the common types of retaining walls.
1. Gravity retaining wall.
2. Cantilever retaining wall.
3. Counter fort retaining wall.
4. Buttress retaining wall.
1. Gravity Retaining Wall
A gravity retaining wall in which the weight of the retaining wall provides stability against the pressure exerted by the backfill
It is made up of stone masonry or plain cement concrete. The principle of design of gravity retaining wall is that tension is not developed anywhere in the section. Therefore, it is designed by using "Middle Third Rule".
2. Cantilever Retaining Wall
The most common and widely used retaining wall is of the cantilever type. Vertical stem resisting earth pressure from one side and the slab bends like a cantilever
Depending upon the soil pressure the thickness of stem slab varies. i.e., larger at bottom and gradually decreased towards top.
The bottom slab is called as toe slab and heel slab both of them act as a horizontal cantilever
A cantilever type of retaining walls are adopted for small to medium height up to 6 m
The stem heel and toe all resist the earth pressure by bending. These walls can be L or inverted T shaped. The weight of the earth on the heel slab and the weight of the retaining wall together provided stability to the wall.
3. Counter fort retaining wall
For height more than 5 m of earth fill the bending moment developed in stem heel and toe slab are very large.
Resulting in larger thickness of structural of structural element and turns to uneconomical section. Hence in this case counter fort type retaining walls are adopted.
Following fig shows a typical counter retaining wall consisting of a stem toe slab heel slab and counter forts.
4. Buttress retaining wall
It is similar to the counter fort retaining wall but with the difference that in buttress retaining wall the counter fort called as buttress are provided on the opposite side of the backfill
It is economical and buttress are design as a compression member but still not preferred buttresses are visible and they occupy the space in front of the wall.
Weep holes are provided to draining the rain water from backfill
Structural behaviour of retaining wall
The retaining wall is a structure that is constructed and constructed to withstand the back pressure of the ground, where there is a desired change in ground height that exceeds the resting angle of the soil
- Gravity wall, cantilever retaining wall, sheet pile retaining wall, bored pile retaining wall, anchored retaining wall are the types of retaining wall are often the types of retaining wall are the types of retaining walls are commonly used.
- Strong storage walls that do not allow to be made are often made as gravity walls. These walls are large in size. However, large gravitational walls may not be operational due to economic and spatial constraints.
- Also, in some cases, adequate pouring of solid cantilever walls can be allowed due to site constraints, and these walls need to be built with higher ground pressures, rather than active ground pressures. One way to deal with these issues is to reduce the focus from the wall.
- There are many ways to reduce the pressure on the ground, such as using a small weight gain. An effort has been made to understand the function of the cantilever wall with auxiliary shelves and therefore to evaluate the performance of the shelves to reduce ground pressure and bending time on the wall.
- The pressure relief shelf is a small cantilever platform with a limited width, extending to the rear angles at right angles, throughout the length of the retaining wall, monolithically constructed with a retaining wall stem.
- The use of an aid shelf not only reduces the pressure on the outside world but also provides economic stability and increases overall stability.
- Klein provides two separate ground pressure distributions namely the non-expanded shelf in the split line (short shelf) and the extended shelf in the split line (long shelf).
- The parameters affecting the structure of a cantilever wall with shelves are the number of shelves, the shape of the shelves and the width of the shelves.
- This paper introduces a parametric study of these factors affecting the construction of a wall using shelves. An effort is being made to find the best shelf space and the right width of shelves by looking at the effect of a short shelf and a long shelf.
- The differences between the base pressure (Pmax) and the minimum pressure (Pmin) in the base are also investigated.
Various force acting on retaining wall
The various force acting on retaining wall are shown in fig.
Self-weight of stem, Toe slab and Heel slab (W4, W2, W3 respectively)
Upward soil pressure
Weight of backfill
Horizontal and vertical earth pressure components
Hence above force is acting on the retaining walls.
The general relation for the coefficient for the coefficient of active earth pressure based on Rankine’s theory is given by the relation.
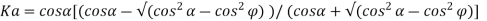
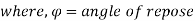
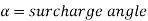
But for level backfill 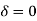
Ka = 1-sin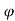 / 1+sin
/ 1+sin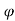
And
Kp 1+sin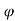 / 1-sin
/ 1-sin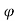
Where Ka and Kp are coefficient of active and passive earth pressure respectively.
Earth pressure for different backfill condition of soil
Dry or moist soil
Submerged soil
Partly submerged soil
Layered soil
Uniform surcharge soil
Inclined backfill
Backfill is horizontal with uniform surcharge w/m at a distance a from stem.
2. Stability requirement
Stability of retaining wall against overturning and sliding
Overturning is one of the limitations of wall stability. In order to improve this post-rear-force analysis it must be tested against the surface of the allocated surface called the thrust surface, usually on the gravitational wall behind the wall, and on cantilever walls it is considered to be a vertical plane
Although Danilevsky (1982) examined the problem in terms of common terms, the stability of anti-displacement walls has been positively assessed by the safety type F, which is defined as the ratio between the resistance times and the number of turning times relative to the toe. So, with the simple cases of Fig. 1, the security item is provided by
F = Wx / Sa d
Where W = the weight of the wall and the soil between the wall and the focus area; Sa = active focus; and x and d = their arms, respectively.
Calculations are usually made using straight and vertical parts of the S, (called Sa and S, respectively). For this purpose, the upper part of the active focus can be considered in two different ways: such as reducing the moment of overturning
F = Wx / Sah ys – Sav X's
Or increasing the resisting moment
F = W x + S a v x s / S a h ys
Where y s and X's = arms of S a h and S a v respectively. Both of these formulas are used in the analysis of wall durability
(Huntington 1957). However, they are fundamentally different. The value of the security feature provided by (3) remains a positive number, and that (2) may divert or subtract negative numbers. Moreover, only (2) is the direct result of (1), while (3) corresponds to the incorrect change of one term from denominator to number.
The design of retaining wall should confirm to the stability requirement specified in IS 456:2000 which includes overturning and sliding
The factor of safety against overturning and sliding should be not less than 1.4
- Overturning
The overturning wall overturns with the toe as the center of rotation
FS (Overturning)= Total restoring moments/Total overturning Moments > 1.55
2. Sliding
The resistance developed against sliding of the retaining wall is mainly due to the frictional force generated between the base slab and supporting soil expressed as,
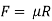
Where
R= Resultant soil pressure acting on the base slab
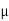 = Coefficient of friction between concrete and soil
= Coefficient of friction between concrete and soil
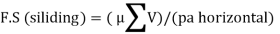
3. Shear key
In case of backfill with discharge the active pressure is relatively high and required factor of safety against sliding by frictional force will not be sufficient.
In such a case it is advantages to provide a shear key projecting below the slab
References:
1. Design of Reinforced Concrete Structure by N. Subramanian, Oxford University Press
2. Limit State Design by A.K. Jain, Neemchand & Bros
3. Reinforced Concrete Design by S U Pillai & D. Menon, McGraw Hill
4. Design of concrete structures by J.N. Bandyopadhyay, PHI
5. Limit State Design of Reinforced Concrete -P.C Verghese