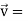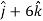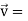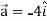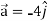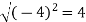Module-3

Vector differential calculus

3.1 Vector and scalar functions and fields, derivative

Vector function-

Suppose 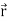be a function of a scalar variable t, then-

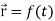
Here vector 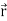varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.

Any vector 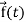 can be expressed as-

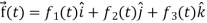
Here , , 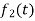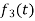are the scalar functions of t.

Differentiation of a vector-

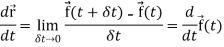
We can denote it as-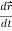

Similarly is the second order derivative of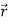

Note- gives the velocity and 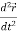gives acceleration.

Note-

1. Velocity =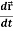

2. Acceleration =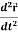

The derivative of the velocity vector V(t) is called acceleration A(t), and it is given as-

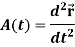
Rules for differentiation-

1.

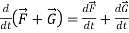
2.

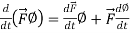
3.

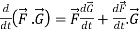
4.

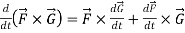
5.

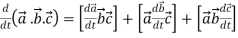
Example-1: A particle moves along the curve 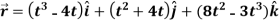, here ‘t’  is the time. Find its velocity and acceleration at t = 2.

Sol. Here we have-

Then, velocity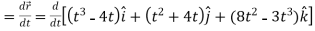

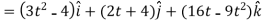
Velocity at t = 2,

=

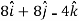
Acceleration =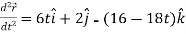

Acceleration at t = 2,

Example-2: If 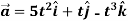and 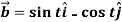then find-

1.

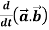
2.

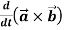
Sol 1. We know that-

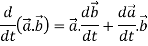
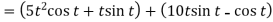
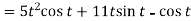
2.

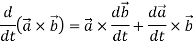
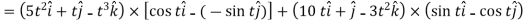
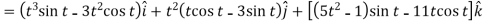
Example-3: A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. then find the velocity and acceleration at time t = 0 and t = π/2.

And find the magnitudes of the velocity and acceleration at time t.

Sol. suppose

Now,

Again acceleration-

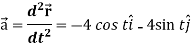
Now-

Scalar point function-

If for each point P of a region R, there corresponds a scalar denoted by f(P), in that case f is called scalar point function of the region R.

Note-

Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).

Vector point function-

If for each point P of a region R, then there corresponds a vector 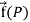then is called a vector point function for the region R.

Vector field-

Vector filed is a reason in space such that with every point P in the region, the vector function associates a vector (P).

Note-

Del operator-

The del operated is defined as-

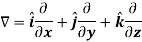
Example: show that 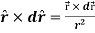 where

Sol. here it is given-

=

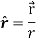
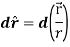
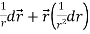
Therefore-

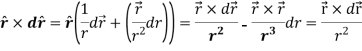
Note-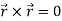

        Hence proved

Key takeaways-

Any vector 

can be expressed as-

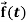
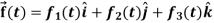
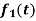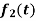Here , , are the scalar functions of t.

1. Velocity =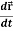

2. Acceleration =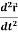

3. Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).

4. Vector field-

Vector filed is a reason in space such that with every point P in the region, the vector function 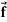associates a vector 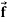(P).

3.2 Tangents and arc Length, curves

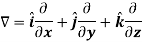
Tangential and normal accelerations-

It is very important to understand that the magnitude of acceleration is not always the rate of change of |V|.

Suppose 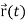be the vector-valued function which denotes the position of any object as a function of time.

Then

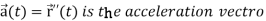
Then the tangential and normal component of acceleration are given as below-

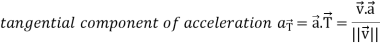
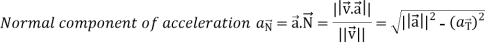
Example: A object move in the path where t is the time in seconds and distance is measured in feets.

Then fi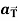nd and 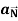as functions of t.

Sol.

We know that-

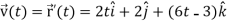
And

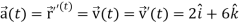
Now we will use-

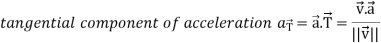
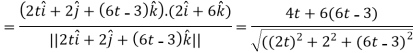
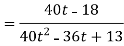
And now-

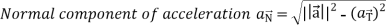
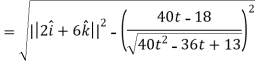
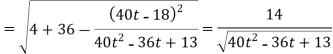
Key takeaways-

3.3           Gradient, divergence and curl

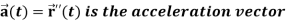
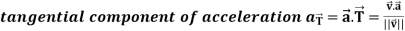
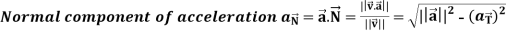
The vector differential operator is written as-

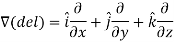
Gradient

Suppose f(x, y, z) be the scalar function and it is continuously differentiable then the vector-

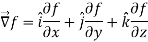
Is called gradient of f and we can write is as grad f.

So that-

Here 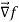is a vector which has three components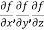

Properties of gradient-

Property-1: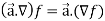

Proof:

First we will take left hand side

                                               L.H.S =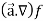

=

=

=

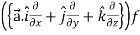
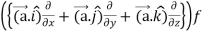
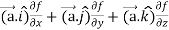
Now taking R.H.S,

                                       R.H.S. =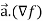

=

=

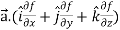
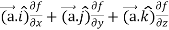
Here-                     L.H.S. = R.H.S.

Hence proved.

Property-2: Gradient of a constant (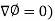

Proof:

Suppose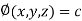

                                              Then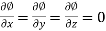

We know that the gradient-

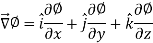
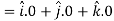
= 0

Property-3: Gradient of the sum and difference of two functions-

If f and g are two scalar point functions, then

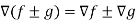
Proof:   

L.H.S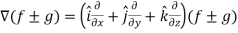                                

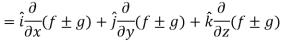
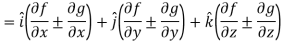
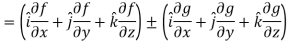
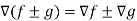
Hence proved

Property-4: Gradient of the product of two functions

If f and g are two scalar point functions, then

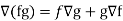
Proof:

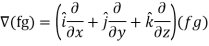
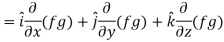
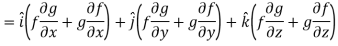
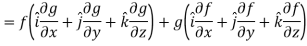
So that-

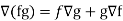
Hence proved.

Property-5: Gradient of the quotient of two functions-

If f and g are two scalar point functions, then-

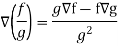
Proof:

So that-

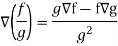
Example-1: If 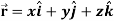, then show that

1.

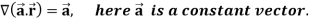
2.

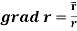
Sol.

Suppose 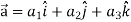  and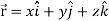

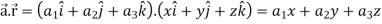
Now taking L.H.S,

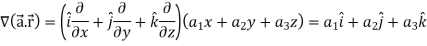
Which is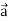

Hence proved.

2.

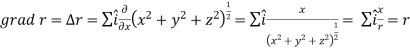
So that

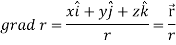
Example: If 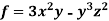then find grad f at the point (1,-2,-1).

Sol.

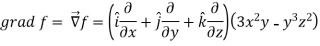
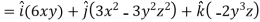
Now grad f at (1 , -2, -1) will be-       

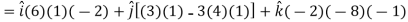
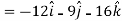
Example: If 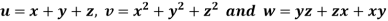then prove that grad u , grad v and grad w are coplanar.

Sol.

Here-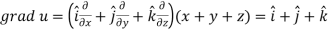                     

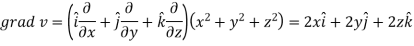
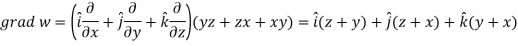
Now-

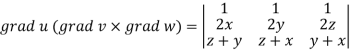
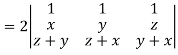
Apply

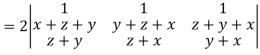
Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.

Divergence (Definition)-

Suppose is a given continuous differentiable vector function then the divergence of this function can be defined as-

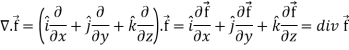
Curl (Definition)-

Curl of a vector function can be defined as-

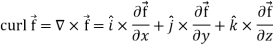
Note- Irrotational vector-

If 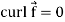then the vector is said to be irrotational.

Vector identities:

Identity-1:  grad uv = u grad v + v grad u

Proof: 

So that

graduv = u grad v + v grad u

Identity-2: 

Proof:

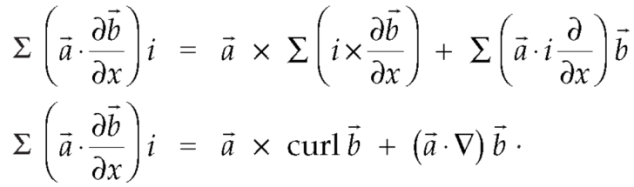
Interchanging 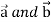, we get-

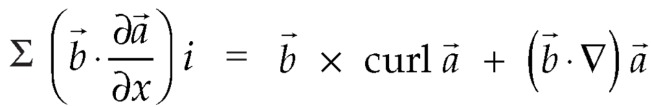
We get by using above equations-

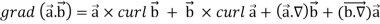
Identity-3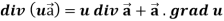

Proof: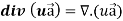   

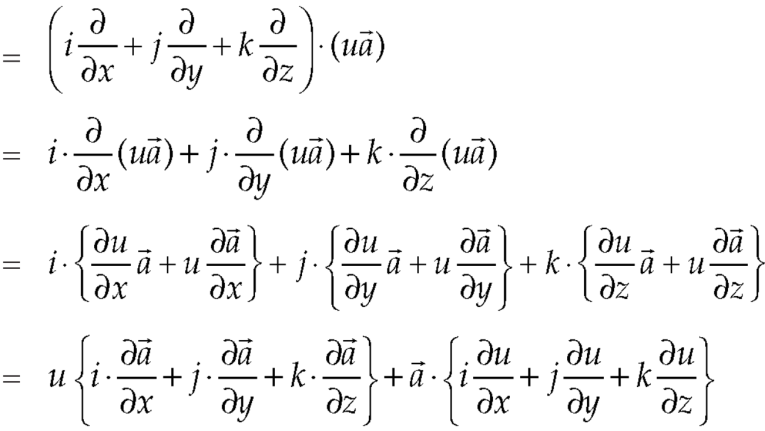
So that-

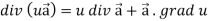
Identity-4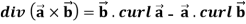

Proof:

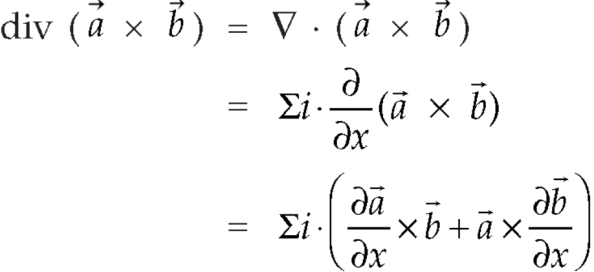
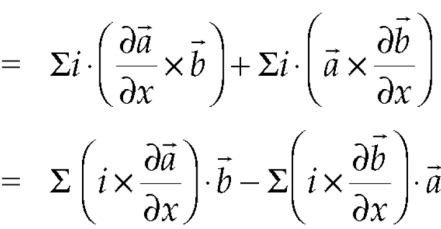
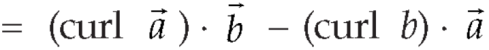
So that,

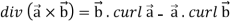
Identity-5       curl (u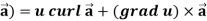

Proof:

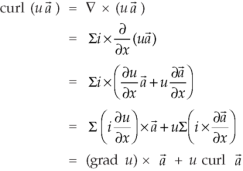
So that

curl (u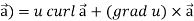

Identity-6: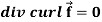

Proof:

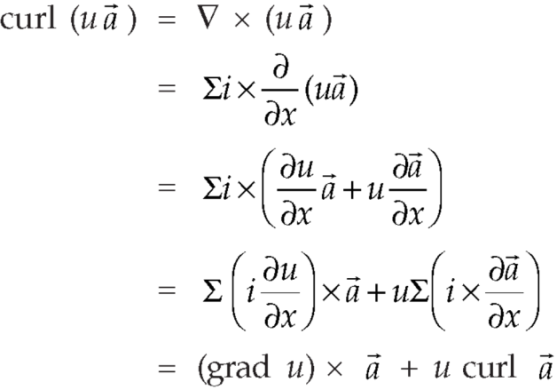
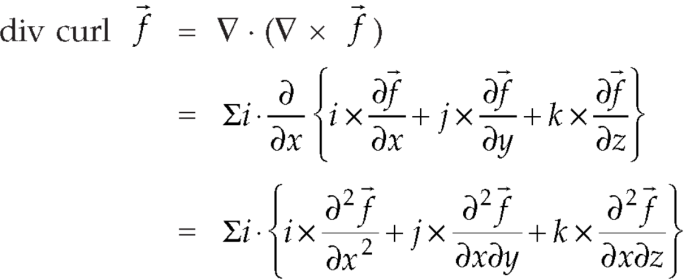
So that-

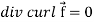
Identity-7: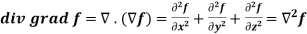

Proof:

So that-

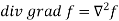
Example-1: Show that-

1.

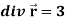
2.

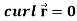
Sol. We know that-

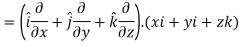
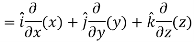
2. We know that-

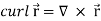
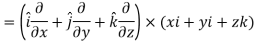
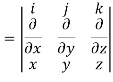
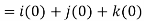= 0

Example-2: If 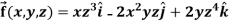then find the divergence and curl of .

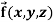Sol.  we know that-

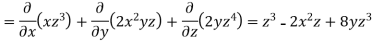
Now-

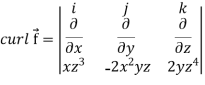
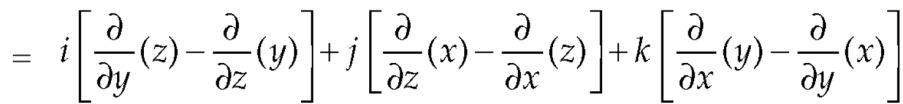
Example-3: Prove that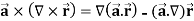

Note- here 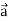is a constant vector and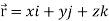

Sol. here    and

So that

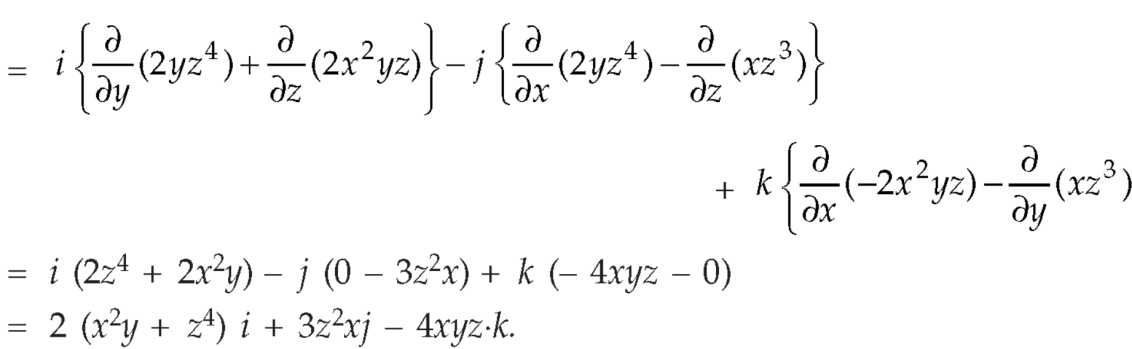
Now-

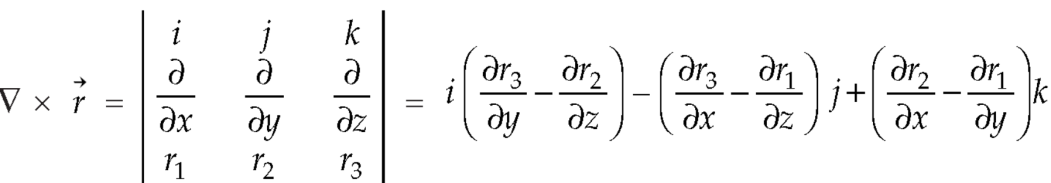
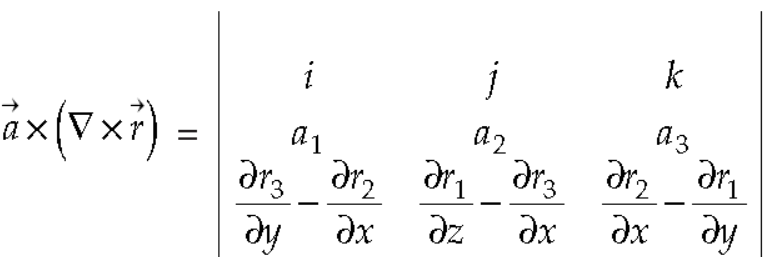
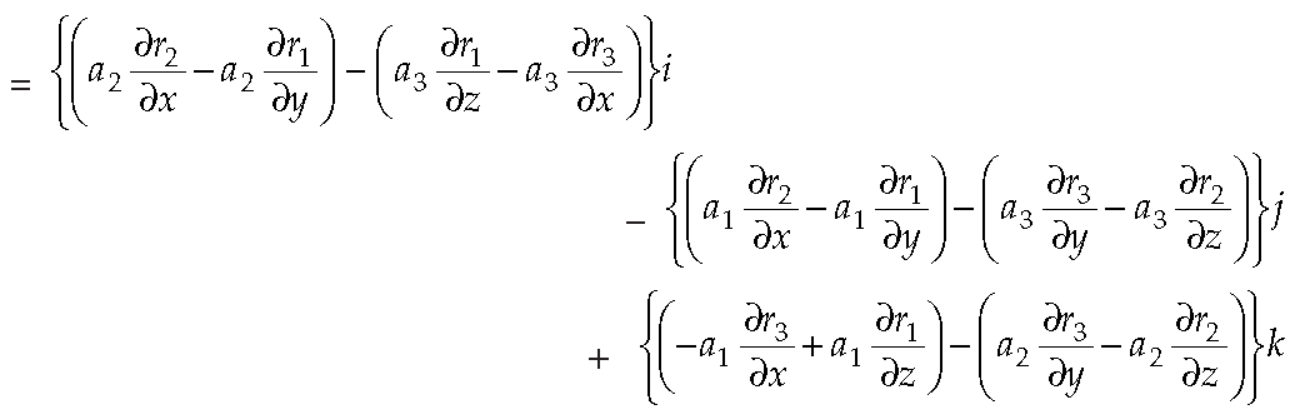
So that-

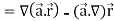
Key takeaways-

Gradient of a constant (

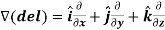
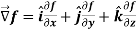
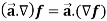
If f and g are two scalar point functions, then

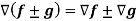
5.      If f and g are two scalar point functions, then

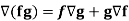
6.      If f and g are two scalar point functions, then-

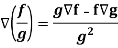
7.     

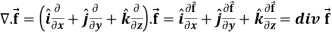
8.     

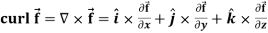
9.      If 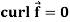then the vector is said to be irrotational.

10.  grad uv = u grad v + v grad u

11. 

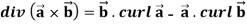
12.  curl (u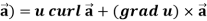

References