Unit - 3
Graph and Tree Algorithms
Traversing the graph means examining all the nodes and vertices of the graph. There are two standard methods by using which, we can traverse the graphs. Let’s discuss each one of them in detail.
Breadth first search is a graph traversal algorithm that starts traversing the graph from root node and explores all the neighbouring nodes. Then, it selects the nearest node and explore all the unexplored nodes. The algorithm follows the same process for each of the nearest node until it finds the goal.
The algorithm of breadth first search is given below. The algorithm starts with examining the node A and all of its neighbours. In the next step, the neighbours of the nearest node of A are explored and process continues in the further steps. The algorithm explores all neighbours of all the nodes and ensures that each node is visited exactly once and no node is visited twice.
for each node in G
and set its STATUS = 2
(waiting state)
QUEUE is empty
and set its STATUS = 3
(processed state).
N that are in the ready state
(whose STATUS = 1) and set
their STATUS = 2
(waiting state)
[END OF LOOP]
Consider the graph G shown in the following image, calculate the minimum path p from node A to node E. Given that each edge has a length of 1.
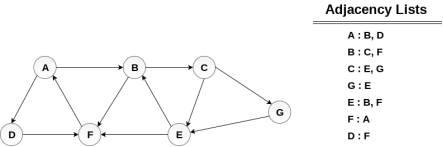
Minimum Path P can be found by applying breadth first search algorithm that will begin at node A and will end at E. the algorithm uses two queues, namely QUEUE1 and QUEUE2. QUEUE1 holds all the nodes that are to be processed while QUEUE2 holds all the nodes that are processed and deleted from QUEUE1.
Let’s start examining the graph from Node A.
1. Add A to QUEUE1 and NULL to QUEUE2.
2. Delete the Node A from QUEUE1 and insert all its neighbours. Insert Node A into QUEUE2
3. Delete the node B from QUEUE1 and insert all its neighbours. Insert node B into QUEUE2.
4. Delete the node D from QUEUE1 and insert all its neighbours. Since F is the only neighbour of it which has been inserted, we will not insert it again. Insert node D into QUEUE2.
5. Delete the node C from QUEUE1 and insert all its neighbours. Add node C to QUEUE2.
6. Remove F from QUEUE1 and add all its neighbours. Since all of its neighbours has already been added, we will not add them again. Add node F to QUEUE2.
7. Remove E from QUEUE1, all of E's neighbours has already been added to QUEUE1 therefore we will not add them again. All the nodes are visited and the target node i.e., E is encountered into QUEUE2.
Now, backtrack from E to A, using the nodes available in QUEUE2.
The minimum path will be A → B → C → E.
Depth first search (DFS) algorithm starts with the initial node of the graph G, and then goes to deeper and deeper until we find the goal node or the node which has no children. The algorithm, then backtracks from the dead end towards the most recent node that is yet to be completely unexplored.
The data structure which is being used in DFS is stack. The process is similar to BFS algorithm. In DFS, the edges that leads to an unvisited node are called discovery edges while the edges that leads to an already visited node are called block edges.
STATUS = 2 (waiting state)
[END OF LOOP]
Example:
Consider the graph G along with its adjacency list, given in the figure below. Calculate the order to print all the nodes of the graph starting from node H, by using depth first search (DFS) algorithm.
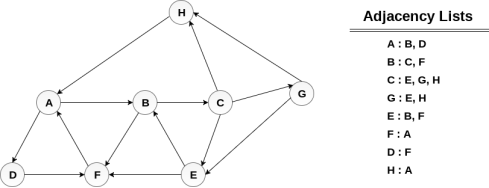
Solution:
Push H onto the stack
POP the top element of the stack i.e., H, print it and push all the neighbours of H onto the stack that are is ready state.
Pop the top element of the stack i.e. A, print it and push all the neighbours of A onto the stack that are in ready state.
Pop the top element of the stack i.e., D, print it and push all the neighbours of D onto the stack that are in ready state.
Pop the top element of the stack i.e., F, print it and push all the neighbours of F onto the stack that are in ready state.
Pop the top of the stack i.e., B and push all the neighbours
Pop the top of the stack i.e., C and push all the neighbours.
Pop the top of the stack i.e., G and push all its neighbours.
Pop the top of the stack i.e., E and push all its neighbours.
Hence, the stack now becomes empty and all the nodes of the graph have been traversed.
The printing sequence of the graph will be:
Solves single shortest path problem in which edge weight may be negative but no negative cycle exists.
This algorithm works correctly when some of the edges of the directed graph G may have negative weight. When there are no cycles of negative weight, then we can find out the shortest path between source and destination.
It is slower than Dijkstra's Algorithm but more versatile, as it capable of handling some of the negative weight edges.
This algorithm detects the negative cycle in a graph and reports their existence.
Based on the "Principle of Relaxation" in which more accurate values gradually recovered an approximation to the proper distance by until eventually reaching the optimum solution.
Given a weighted directed graph G = (V, E) with source s and weight function w: E → R, the Bellman-Ford algorithm returns a Boolean value indicating whether or not there is a negative weight cycle that is attainable from the source. If there is such a cycle, the algorithm produces the shortest paths and their weights. The algorithm returns TRUE if and only if a graph contains no negative - weight cycles that are reachable from the source.
distk [u] = [min [distk-1 [u], min [ distk-1 [i]+cost [i, u]]] as i except u.
k → k is the source vertex
u → u is the destination vertex
i → no of edges to be scanned concerning a vertex.
BELLMAN -FORD (G, w, s)
1. INITIALIZE - SINGLE - SOURCE (G, s)
2. for i ← 1 to |V[G]| - 1
3. do for each edge (u, v) ∈ E [G]
4. do RELAX (u, v, w)
5. for each edge (u, v) ∈ E [G]
6. do if d [v] > d [u] + w (u, v)
7. then return FALSE.
8. return TRUE.
Example: Here first we list all the edges and their weights.
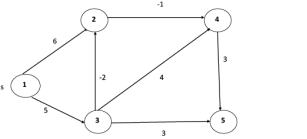
Solution:
distk [u] = [min [distk-1 [u], min [distk-1 [i]+cost [i, u]]] as i ≠ u.
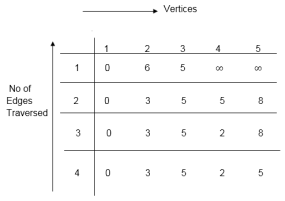
dist2 [2]=min[dist1 [2],min[dist1 [1]+cost[1,2],dist1 [3]+cost[3,2],dist1 [4]+cost[4,2],dist1 [5]+cost[5,2]]]
Min = [6, 0 + 6, 5 + (-2), ∞ + ∞ , ∞ +∞] = 3
dist2 [3]=min[dist1 [3],min[dist1 [1]+cost[1,3],dist1 [2]+cost[2,3],dist1 [4]+cost[4,3],dist1 [5]+cost[5,3]]]
Min = [5, 0 +∞, 6 +∞, ∞ + ∞ , ∞ + ∞] = 5
dist2 [4]=min[dist1 [4],min[dist1 [1]+cost[1,4],dist1 [2]+cost[2,4],dist1 [3]+cost[3,4],dist1 [5]+cost[5,4]]]
Min = [∞, 0 +∞, 6 + (-1), 5 + 4, ∞ +∞] = 5
dist2 [5]=min[dist1 [5],min[dist1 [1]+cost[1,5],dist1 [2]+cost[2,5],dist1 [3]+cost[3,5],dist1 [4]+cost[4,5]]]
Min = [∞, 0 + ∞,6 + ∞,5 + 3, ∞ + 3] = 8
dist3 [2]=min[dist2 [2],min[dist2 [1]+cost[1,2],dist2 [3]+cost[3,2],dist2 [4]+cost[4,2],dist2 [5]+cost[5,2]]]
Min = [3, 0 + 6, 5 + (-2), 5 + ∞ , 8 + ∞ ] = 3
dist3 [3]=min[dist2 [3],min[dist2 [1]+cost[1,3],dist2 [2]+cost[2,3],dist2 [4]+cost[4,3],dist2 [5]+cost[5,3]]]
Min = [5, 0 + ∞, 3 + ∞, 5 + ∞,8 + ∞ ] = 5
dist3 [4]=min[dist2 [4],min[dist2 [1]+cost[1,4],dist2 [2]+cost[2,4],dist2 [3]+cost[3,4],dist2 [5]+cost[5,4]]]
Min = [5, 0 + ∞, 3 + (-1), 5 + 4, 8 + ∞ ] = 2
dist3 [5]=min[dist2 [5],min[dist2 [1]+cost[1,5],dist2 [2]+cost[2,5],dist2 [3]+cost[3,5],dist2 [4]+cost[4,5]]]
Min = [8, 0 + ∞, 3 + ∞, 5 + 3, 5 + 3] = 8
dist4 [2]=min[dist3 [2],min[dist3 [1]+cost[1,2],dist3 [3]+cost[3,2],dist3 [4]+cost[4,2],dist3 [5]+cost[5,2]]]
Min = [3, 0 + 6, 5 + (-2), 2 + ∞, 8 + ∞ ] =3
dist4 [3]=min[dist3 [3],min[dist3 [1]+cost[1,3],dist3 [2]+cost[2,3],dist3 [4]+cost[4,3],dist3 [5]+cost[5,3]]]
Min = 5, 0 + ∞, 3 + ∞, 2 + ∞, 8 + ∞ ] =5
dist4 [4]=min[dist3 [4],min[dist3 [1]+cost[1,4],dist3 [2]+cost[2,4],dist3 [3]+cost[3,4],dist3 [5]+cost[5,4]]]
Min = [2, 0 + ∞, 3 + (-1), 5 + 4, 8 + ∞ ] = 2
dist4 [5]=min[dist3 [5],min[dist3 [1]+cost[1,5],dist3 [2]+cost[2,5],dist3 [3]+cost[3,5],dist3 [5]+cost[4,5]]]
Min = [8, 0 +∞, 3 + ∞, 8, 5] = 5
It is a greedy algorithm that solves the single-source shortest path problem for a directed graph G = (V, E) with nonnegative edge weights, i.e., w (u, v) ≥ 0 for each edge (u, v) ∈ E.
Dijkstra's Algorithm maintains a set S of vertices whose final shortest - path weights from the source s have already been determined. That's for all vertices v ∈ S; we have d [v] = δ (s, v). The algorithm repeatedly selects the vertex u ∈ V - S with the minimum shortest - path estimate, insert u into S and relaxes all edges leaving u.
Because it always chooses the "lightest" or "closest" vertex in V - S to insert into set S, it is called as the greedy strategy.
Dijkstra's Algorithm (G, w, s)
1. INITIALIZE - SINGLE - SOURCE (G, s)
2. S←∅
3. Q←V [G]
4. while Q ≠ ∅
5. do u ← EXTRACT - MIN (Q)
6. S ← S ∪ {u}
7. for each vertex v ∈ Adj [u]
8. do RELAX (u, v, w)
Analysis: The running time of Dijkstra's algorithm on a graph with edges E and vertices V can be expressed as a function of |E| and |V| using the Big - O notation. The simplest implementation of the Dijkstra's algorithm stores vertices of set Q in an ordinary linked list or array, and operation Extract - Min (Q) is simply a linear search through all vertices in Q. In this case, the running time is O (|V2 |+|E|=O (V2).
Example:
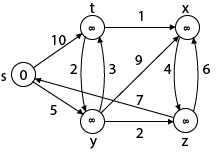
Solution:
Step1: Q = [s, t, x, y, z]
We scanned vertices one by one and find out its adjacent. Calculate the distance of each adjacent to the source vertices.
We make a stack, which contains those vertices which are selected after computation of shortest distance.
Firstly, we take's' in stack M (which is a source)
Step 2: Now find the adjacent of s that are t and y.

Case - (i) s → t
d [v] > d [u] + w [u, v]
d [t] > d [s] + w [s, t]
∞ > 0 + 10 [false condition]
Then d [t] ← 10
π [t] ← 5
Adj [s] ← t, y
Case - (ii) s→ y
d [v] > d [u] + w [u, v]
d [y] > d [s] + w [s, y]
∞ > 0 + 5 [false condition]
∞ > 5
Then d [y] ← 5
π [y] ← 5
By comparing case (i) and case (ii)
Adj [s] → t = 10, y = 5
y is shortest
y is assigned in 5 = [s, y]
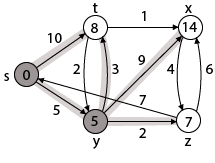
Step 3: Now find the adjacent of y that is t, x, z.
Case - (i) y →t
d [v] > d [u] + w [u, v]
d [t] > d [y] + w [y, t]
10 > 5 + 3
10 > 8
Then d [t] ← 8
π [t] ← y
Case - (ii) y → x
d [v] > d [u] + w [u, v]
d [x] > d [y] + w [y, x]
∞ > 5 + 9
∞ > 14
Then d [x] ← 14
π [x] ← 14
Case - (iii) y → z
d [v] > d [u] + w [u, v]
d [z] > d [y] + w [y, z]
∞ > 5 + 2
∞ > 7
Then d [z] ← 7
π [z] ← y
By comparing case (i), case (ii) and case (iii)
Adj [y] → x = 14, t = 8, z =7
z is shortest
z is assigned in 7 = [s, z]
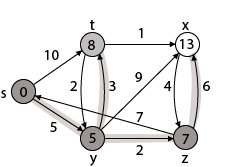
Step - 4 Now we will find adj [z] that are s, x
Case - (i) z → x
d [v] > d [u] + w [u, v]
d [x] > d [z] + w [z, x]
14 > 7 + 6
14 > 13
Then d [x] ← 13
π [x] ← z
Case - (ii) z → s
d [v] > d [u] + w [u, v]
d [s] > d [z] + w [z, s]
0 > 7 + 7
0 > 14
∴ This condition does not satisfy so it will be discarded.
Now we have x = 13.
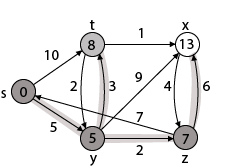
Step 5: Now we will find Adj [t]
Adj [t] → [x, y] [Here t is u and x and y are v]
Case - (i) t → x
d [v] > d [u] + w [u, v]
d [x] > d [t] + w [t, x]
13 > 8 + 1
13 > 9
Then d [x] ← 9
π [x] ← t
Case - (ii) t → y
d [v] > d [u] + w [u, v]
d [y] > d [t] + w [t, y]
5 > 10
∴ This condition does not satisfy so it will be discarded.
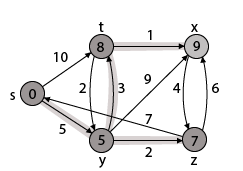
Thus, we get all shortest path vertex as
Weight from s to y is 5
Weight from s to z is 7
Weight from s to t is 8
Weight from s to x is 9
These are the shortest distance from the source's' in the given graph.
Disadvantage of Dijkstra's Algorithm:
in Dijkstra’s algorithm, two sets are maintained, one set contains list of vertices already included in SPT (Shortest Path Tree), other set contains vertices not yet included. With adjacency list representation, all vertices of a graph can be traversed in O(V+E) time using BFS. The idea is to traverse all vertices of graph using BFS and use a Min Heap to store the vertices not yet included in SPT (or the vertices for which shortest distance is not finalized yet). Min Heap is used as a priority queue to get the minimum distance vertex from set of not yet included vertices. Time complexity of operations like extract-min and decrease-key value is O(LogV) for Min Heap.
Following are the detailed steps.
1) Create a Min Heap of size V where V is the number of vertices in the given graph. Every node of min heap contains vertex number and distance value of the vertex.
2) Initialize Min Heap with source vertex as root (the distance value assigned to source vertex is 0). The distance value assigned to all other vertices is INF (infinite).
3) While Min Heap is not empty, do following
…...a) Extract the vertex with minimum distance value node from Min Heap. Let the extracted vertex be u.
…...b) For every adjacent vertex v of u, check if v is in Min Heap. If v is in Min Heap and distance value is more than weight of u-v plus distance value of u, then update the distance value of v.
Let us understand with the following example. Let the given source vertex be 0
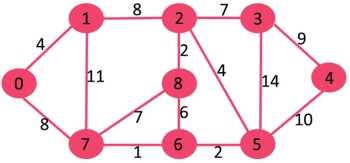
Initially, distance value of source vertex is 0 and INF (infinite) for all other vertices. So, source vertex is extracted from Min Heap and distance values of vertices adjacent to 0 (1 and 7) are updated. Min Heap contains all vertices except vertex 0.
The vertices in green color are the vertices for which minimum distances are finalized and are not in Min Heap
Since distance value of vertex 1 is minimum among all nodes in Min Heap, it is extracted from Min Heap and distance values of vertices adjacent to 1 are updated (distance is updated if a vertex is in Min Heap and distance through 1 is shorter than the previous distance). Min Heap contains all vertices except vertex 0 and 1.
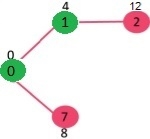
Pick the vertex with minimum distance value from min heap. Vertex 7 is picked. So, min heap now contains all vertices except 0, 1 and 7. Update the distance values of adjacent vertices of 7. The distance value of vertex 6 and 8 becomes finite (15 and 9 respectively).
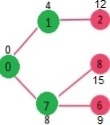
Pick the vertex with minimum distance from min heap. Vertex 6 is picked. So, min heap now contains all vertices except 0, 1, 7 and 6. Update the distance values of adjacent vertices of 6. The distance value of vertex 5 and 8 are updated.
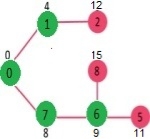
Above steps are repeated till min heap doesn’t become empty. Finally, we get the following shortest path tree.
// C / C++ program for Dijkstra's // shortest path algorithm for adjacency // list representation of graph #include <stdio.h> #include <stdlib.h> #include <limits.h>
// A structure to represent a // node in adjacency list struct AdjListNode { int dest; int weight; struct AdjListNode* next; };
// A structure to represent // an adjacency list struct AdjList {
// Pointer to head node of list struct AdjListNode *head; };
// A structure to represent a graph. // A graph is an array of adjacency lists. // Size of array will be V (number of // vertices in graph) struct Graph { int V; struct AdjList* array; };
// A utility function to create // a new adjacency list node struct AdjListNode* newAdjListNode( int dest, int weight) { struct AdjListNode* newNode = (struct AdjListNode*) malloc(sizeof(struct AdjListNode)); newNode->dest = dest; newNode->weight = weight; newNode->next = NULL; return newNode; }
// A utility function that creates // a graph of V vertices struct Graph* createGraph(int V) { struct Graph* graph = (struct Graph*) malloc(sizeof(struct Graph)); graph->V = V;
// Create an array of adjacency lists. // Size of array will be V graph->array = (struct AdjList*) malloc(V * sizeof(struct AdjList));
// Initialize each adjacency list // as empty by making head as NULL for (int i = 0; i < V; ++i) graph->array[i].head = NULL;
return graph; }
// Adds an edge to an undirected graph void addEdge(struct Graph* graph, int src, int dest, int weight) { // Add an edge from src to dest. // A new node is added to the adjacency // list of src. The node is // added at the beginning struct AdjListNode* newNode = newAdjListNode(dest, weight); newNode->next = graph->array[src].head; graph->array[src].head = newNode;
// Since graph is undirected, // add an edge from dest to src also newNode = newAdjListNode(src, weight); newNode->next = graph->array[dest].head; graph->array[dest].head = newNode; }
// Structure to represent a min heap node struct MinHeapNode { int v; int dist; };
// Structure to represent a min heap struct MinHeap {
// Number of heap nodes present currently int size;
// Capacity of min heap int capacity;
// This is needed for decreaseKey() int *pos; struct MinHeapNode **array; };
// A utility function to create a // new Min Heap Node struct MinHeapNode* newMinHeapNode(int v, int dist) { struct MinHeapNode* minHeapNode = (struct MinHeapNode*) malloc(sizeof(struct MinHeapNode)); minHeapNode->v = v; minHeapNode->dist = dist; return minHeapNode; }
// A utility function to create a Min Heap struct MinHeap* createMinHeap(int capacity) { struct MinHeap* minHeap = (struct MinHeap*) malloc(sizeof(struct MinHeap)); minHeap->pos = (int *)malloc( capacity * sizeof(int)); minHeap->size = 0; minHeap->capacity = capacity; minHeap->array = (struct MinHeapNode**) malloc(capacity * sizeof(struct MinHeapNode*)); return minHeap; }
// A utility function to swap two // nodes of min heap. // Needed for min heapify void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b) { struct MinHeapNode* t = *a; *a = *b; *b = t; }
// A standard function to // heapify at given idx // This function also updates // position of nodes when they are swapped. // Position is needed for decreaseKey() void minHeapify(struct MinHeap* minHeap, int idx) { int smallest, left, right; smallest = idx; left = 2 * idx + 1; right = 2 * idx + 2;
if (left < minHeap->size && minHeap->array[left]->dist < minHeap->array[smallest]->dist ) smallest = left;
if (right < minHeap->size && minHeap->array[right]->dist < minHeap->array[smallest]->dist ) smallest = right;
if (smallest != idx) { // The nodes to be swapped in min heap MinHeapNode *smallestNode = minHeap->array[smallest]; MinHeapNode *idxNode = minHeap->array[idx];
// Swap positions minHeap->pos[smallestNode->v] = idx; minHeap->pos[idxNode->v] = smallest;
// Swap nodes swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]);
minHeapify(minHeap, smallest); } }
// A utility function to check if // the given minHeap is ampty or not int isEmpty(struct MinHeap* minHeap) { return minHeap->size == 0; }
// Standard function to extract // minimum node from heap struct MinHeapNode* extractMin(struct MinHeap* minHeap) { if (isEmpty(minHeap)) return NULL;
// Store the root node struct MinHeapNode* root = minHeap->array[0];
// Replace root node with last node struct MinHeapNode* lastNode = minHeap->array[minHeap->size - 1]; minHeap->array[0] = lastNode;
// Update position of last node minHeap->pos[root->v] = minHeap->size-1; minHeap->pos[lastNode->v] = 0;
// Reduce heap size and heapify root --minHeap->size; minHeapify(minHeap, 0);
return root; }
// Function to decreasy dist value // of a given vertex v. This function // uses pos[] of min heap to get the // current index of node in min heap void decreaseKey(struct MinHeap* minHeap, int v, int dist) { // Get the index of v in heap array int i = minHeap->pos[v];
// Get the node and update its dist value minHeap->array[i]->dist = dist;
// Travel up while the complete // tree is not hepified. // This is a O(Logn) loop while (i && minHeap->array[i]->dist < minHeap->array[(i - 1) / 2]->dist) { // Swap this node with its parent minHeap->pos[minHeap->array[i]->v] = (i-1)/2; minHeap->pos[minHeap->array[ (i-1)/2]->v] = i; swapMinHeapNode(&minHeap->array[i], &minHeap->array[(i - 1) / 2]);
// move to parent index i = (i - 1) / 2; } }
// A utility function to check if a given vertex // 'v' is in min heap or not bool isInMinHeap(struct MinHeap *minHeap, int v) { if (minHeap->pos[v] < minHeap->size) return true; return false; }
// A utility function used to print the solution void printArr(int dist[], int n) { printf("Vertex Distance from Source\n"); for (int i = 0; i < n; ++i) printf("%d \t\t %d\n", i, dist[i]); }
// The main function that calulates // distances of shortest paths from src to all // vertices. It is a O(ELogV) function void dijkstra(struct Graph* graph, int src) {
// Get the number of vertices in graph int V = graph->V;
// dist values used to pick // minimum weight edge in cut int dist[V];
// minHeap represents set E struct MinHeap* minHeap = createMinHeap(V);
// Initialize min heap with all // vertices. dist value of all vertices for (int v = 0; v < V; ++v) { dist[v] = INT_MAX; minHeap->array[v] = newMinHeapNode(v, dist[v]); minHeap->pos[v] = v; }
// Make dist value of src vertex // as 0 so that it is extracted first minHeap->array[src] = newMinHeapNode(src, dist[src]); minHeap->pos[src] = src; dist[src] = 0; decreaseKey(minHeap, src, dist[src]);
// Initially size of min heap is equal to V minHeap->size = V;
// In the followin loop, // min heap contains all nodes // whose shortest distance // is not yet finalized. while (!isEmpty(minHeap)) { // Extract the vertex with // minimum distance value struct MinHeapNode* minHeapNode = extractMin(minHeap);
// Store the extracted vertex number int u = minHeapNode->v;
// Traverse through all adjacent // vertices of u (the extracted // vertex) and update // their distance values struct AdjListNode* pCrawl = graph->array[u].head; while (pCrawl != NULL) { int v = pCrawl->dest;
// If shortest distance to v is // not finalized yet, and distance to v // through u is less than its // previously calculated distance if (isInMinHeap(minHeap, v) && dist[u] != INT_MAX && pCrawl->weight + dist[u] < dist[v]) { dist[v] = dist[u] + pCrawl->weight;
// update distance // value in min heap also decreaseKey(minHeap, v, dist[v]); } pCrawl = pCrawl->next; } }
// print the calculated shortest distances printArr(dist, V); }
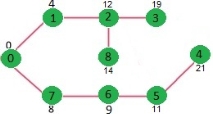
// Driver program to test above functions int main() { // create the graph given in above fugure int V = 9; struct Graph* graph = createGraph(V); addEdge(graph, 0, 1, 4); addEdge(graph, 0, 7, 8); addEdge(graph, 1, 2, 8); addEdge(graph, 1, 7, 11); addEdge(graph, 2, 3, 7); addEdge(graph, 2, 8, 2); addEdge(graph, 2, 5, 4); addEdge(graph, 3, 4, 9); addEdge(graph, 3, 5, 14); addEdge(graph, 4, 5, 10); addEdge(graph, 5, 6, 2); addEdge(graph, 6, 7, 1); addEdge(graph, 6, 8, 6); addEdge(graph, 7, 8, 7);
dijkstra(graph, 0);
return 0; } |
Output:
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14
Time Complexity: The time complexity of the above code/algorithm looks O(V^2) as there are two nested while loops. If we take a closer look, we can observe that the statements in inner loop are executed O(V+E) times (similar to BFS). The inner loop has decrease Key () operation which takes O(Log V) time. So overall time complexity is O(E+V) *O(Log V) which is O((E+V) *Log V) = O(E Log V)
Note that the above code uses Binary Heap for Priority Queue implementation. Time complexity can be reduced to O (E + VLogV) using Fibonacci Heap. The reason is, Fibonacci Heap takes O (1) time for decrease-key operation while Binary Heap takes O(Logn) time.
Notes:
Let the vertices of G be V = {1, 2........n} and consider a subset {1, 2........k} of vertices for some k. For any pair of vertices i, j ∈ V, considered all paths from i to j whose intermediate vertices are all drawn from {1, 2.......k}, and let p be a minimum weight path from amongst them. The Floyd-Warshall algorithm exploits a link between path p and shortest paths from i to j with all intermediate vertices in the set {1, 2.......k-1}. The link depends on whether or not k is an intermediate vertex of path p.
If k is not an intermediate vertex of path p, then all intermediate vertices of path p are in the set {1, 2........k-1}. Thus, the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k-1} is also the shortest path i to j with all intermediate vertices in the set {1, 2.......k}.
If k is an intermediate vertex of path p, then we break p down into i → k → j.
Let dij(k) be the weight of the shortest path from vertex i to vertex j with all intermediate vertices in the set {1, 2.......k}.
A recursive definition is given by
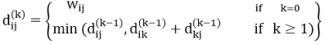
FLOYD - WARSHALL (W)
n ← rows [W].
D0 ← W
for k ← 1 to n
do for i ← 1 to n
do for j ← 1 to n
do dij(k) ← min (dij(k-1), dik(k-1) +dkj(k-1))
return D(n)
The strategy adopted by the Floyd-Warshall algorithm is Dynamic Programming. The running time of the Floyd-Warshall algorithm is determined by the triply nested for loops of lines 3-6. Each execution of line 6 takes O (1) time. The algorithm thus runs in time θ (n3).
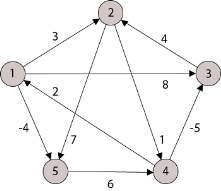
Example: Apply Floyd-Warshall algorithm for constructing the shortest path. Show that matrices D(k) and π(k) computed by the Floyd-Warshall algorithm for the graph.
Solution:
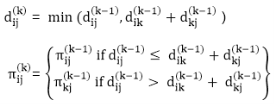
Step (i) When k = 0

Step (ii) When k =1
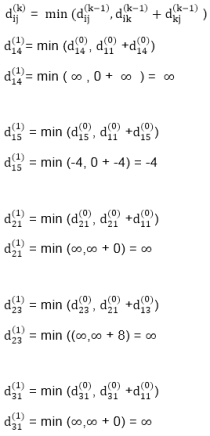
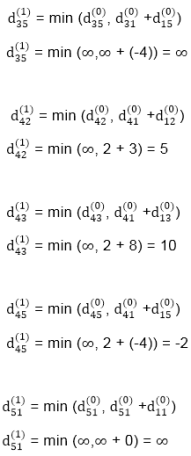

Step (iii) When k = 2
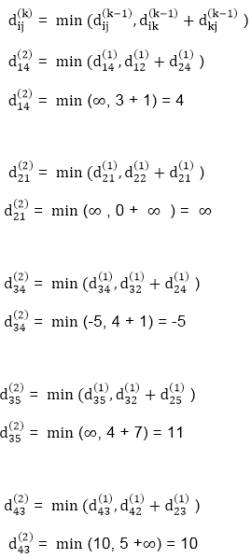

Step (iv) When k = 3
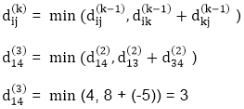
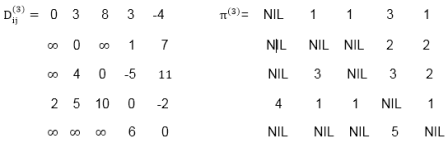
Step (v) When k = 4
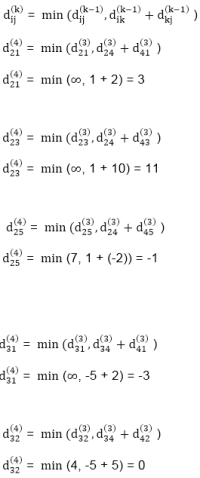
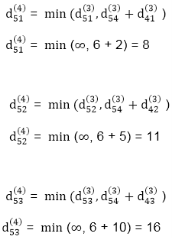

Step (vi) When k = 5
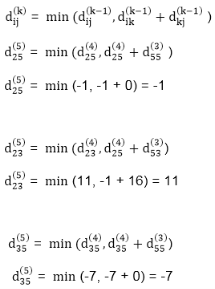
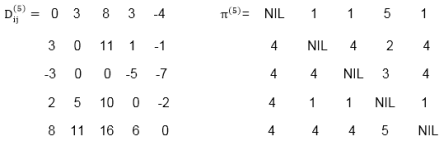
TRANSITIVE- CLOSURE (G)
1. n ← |V[G]|
2. for i ← 1 to n
3. do for j ← 1 to n
4. do if i = j or (i, j) ∈ E [G]
5. the 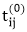 ← 1
← 1
6. else 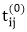 ← 0
← 0
7. for k ← 1 to n
8. do for i ← 1 to n
9. do for j ← 1 to n
10. dod ij(k) ← 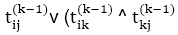
11. Return T(n).
Key takeaways:
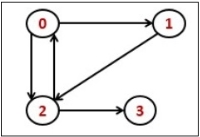
Transitive Closure it the reachability matrix to reach from vertex u to vertex v of a graph. One graph is given, we have to find a vertex v which is reachable from another vertex u, for all vertex pairs (u, v).
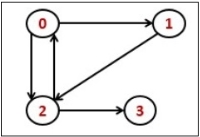
Fig 4 - Transitive Closure
The final matrix is the Boolean type. When there is a value 1 for vertex u to vertex v, it means that there is at least one path from u to v.
Input:
1 1 0 1
0 1 1 0
0 0 1 1
0 0 0 1
Output:
The matrix of transitive closure
1 1 1 1
0 1 1 1
0 0 1 1
0 0 0 1
transColsure(graph)
Input: The given graph.
Output: Transitive Closure matrix.
Begin
copy the adjacency matrix into another matrix named transMat
for any vertex k in the graph, do
for each vertex i in the graph, do
for each vertex j in the graph, do
transMat[i, j] := transMat[i, j] OR (transMat[i, k]) AND transMat[k, j])
done
done
done
Display the transMat
End
<2>Example
#include<iostream>
#include<vector>
#define NODE 4
using namespace std;
/* int graph[NODE][NODE] = {
{0, 1, 1, 0},
{0, 0, 1, 0},
{1, 0, 0, 1},
{0, 0, 0, 0}
}; */
int graph[NODE][NODE] = {
{1, 1, 0, 1},
{0, 1, 1, 0},
{0, 0, 1, 1},
{0, 0, 0, 1}
};
int result[NODE][NODE];
void transClosure() {
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
result[i][j] = graph[i][j]; //initially copy the graph to the result matrix
for(int k = 0; k<NODE; k++)
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
result[i][j] = result[i][j] || (result[i][k] && result[k][j]);
for(int i = 0; i<NODE; i++) { //print the result matrix
for(int j = 0; j<NODE; j++)
cout << result[i][j] << " ";
cout << endl;
}
}
int main() {
transClosure();
}
1 1 1 1
0 1 1 1
0 0 1 1
0 0 0 1
Key takeaways:
Transitive Closure it the reachability matrix to reach from vertex u to vertex v of a graph. One graph is given, we have to find a vertex v which is reachable from another vertex u, for all vertex pairs (u, v).
The final matrix is the Boolean type. When there is a value 1 for vertex u to vertex v, it means that there is at least one path from u to v.
The topological sorting for a directed acyclic graph is the linear ordering of vertices. For every edge U-V of a directed graph, the vertex u will come before vertex v in the ordering.
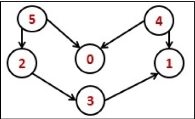
Fig 5 - Topological sorting
As we know that the source vertex will come after the destination vertex, so we need to use a stack to store previous elements. After completing all nodes, we can simply display them from the stack.
Input:
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
1 1 0 0 0 0
1 0 1 0 0 0
Output:
Nodes after topological sorted order: 5 4 2 3 1 0
topoSort (u, visited, stack)
Input − The start vertex u, an array to keep track of which node is visited or not. A stack to store nodes.
Output − Sorting the vertices in topological sequence in the stack.
Begin
mark u as visited
for all vertices v which is adjacent with u, do
if v is not visited, then
topoSort(c, visited, stack)
done
push u into a stack
End
performTopologicalSorting(Graph)
Input − The given directed acyclic graph.
Output − Sequence of nodes.
Begin
initially mark all nodes as unvisited
for all nodes v of the graph, do
if v is not visited, then
topoSort(i, visited, stack)
done
pop and print all elements from the stack
End.
#include<iostream>
#include<stack>
#define NODE 6
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0},
{0, 1, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void performTopologicalSort() {
stack<int> stk;
bool vis[NODE];
for(int i = 0; i<NODE; i++)
vis[i] = false; //initially all nodes are unvisited
for(int i = 0; i<NODE; i++)
if(!vis[i]) //when node is not visited
topoSort(i, vis, stk);
while(!stk.empty()) {
cout << stk.top() << " ";
stk.pop();
}
}
main() {
cout << "Nodes after topological sorted order: ";
performTopologicalSort();
}
Key takeaways:
The topological sorting for a directed acyclic graph is the linear ordering of vertices. For every edge U-V of a directed graph, the vertex u will come before vertex v in the ordering.
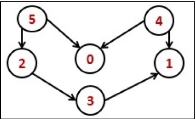
As we know that the source vertex will come after the destination vertex, so we need to use a stack to store previous elements. After completing all nodes, we can simply display them from the stack.
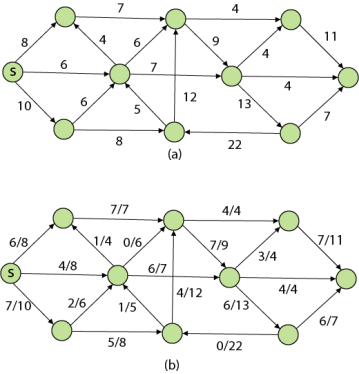
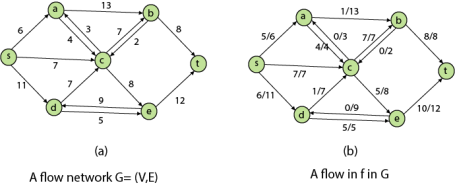
Flow Network is a directed graph that is used for modeling material Flow. There are two different vertices; one is a source which produces material at some steady rate, and another one is sink which consumes the content at the same constant speed. The flow of the material at any mark in the system is the rate at which the element moves.
Some real-life problems like the flow of liquids through pipes, the current through wires and delivery of goods can be modeled using flow networks.
Definition: A Flow Network is a directed graph G = (V, E) such that
Let G = (V, E) be a flow network. Let s be the source of the network, and let t be the sink. A flow in G is a real-valued function f: V x V→R such that the following properties hold:
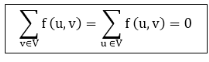
The quantity f (u, v), which can be positive or negative, is known as the net flow from vertex u to vertex v. In the maximum-flow problem, we are given a flow network G with source s and sink t, and we wish to find a flow of maximum value from s to t.
The three properties can be described as follows:
The value of the flow is the net flow from the source,
The positive net flow entering a vertex v is described by
The positive net flow leaving a vertex is described symmetrically. One interpretation of the Flow-Conservation Property is that the positive net flow entering a vertex other than the source or sink must equal the positive net flow leaving the vertex.
A flow f is said to be integer-valued if f (u, v) is an integer for all (u, v) ∈ E. Clearly, the value of the flow is an integer is an integer-valued flow.
The most obvious flow network problem is the following:
Problem1: Given a flow network G = (V, E), the maximum flow problem is to find a flow with maximum value.
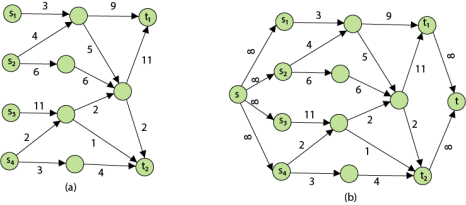
Problem 2: The multiple sources and sink maximum flow problem is similar to the maximum flow problem, except there is a set {s1, s2, s3.......sn} of sources and a set {t1, t2, t3..........tn} of sinks.
Fortunately, this problem is no solid than regular maximum flow. Given multiple sources and sink flow network G, we define a new flow network G' by adding
Figure shows multiple sources and sinks flow network and an equivalent single source and sink flow network
Residual Networks: The Residual Network consists of an edge that can admit more net flow. Suppose we have a flow network G = (V, E) with source s and sink t. Let f be a flow in G, and examine a pair of vertices u, v ∈ V. The sum of additional net flow we can push from u to v before exceeding the capacity c (u, v) is the residual capacity of (u, v) given by
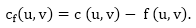
When the net flow f (u, v) is negative, the residual capacity cf (u, v) is greater than the capacity c (u, v).
For Example: if c (u, v) = 16 and f (u, v) =16 and f (u, v) = -4, then the residual capacity cf (u, v) is 20.
Given a flow network G = (V, E) and a flow f, the residual network of G induced by f is Gf = (V, Ef), where
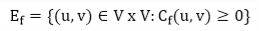
That is, each edge of the residual network, or residual edge, can admit a strictly positive net flow.
Augmenting Path: Given a flow network G = (V, E) and a flow f, an augmenting path p is a simple path from s to t in the residual network Gf. By the solution of the residual network, each edge (u, v) on an augmenting path admits some additional positive net flow from u to v without violating the capacity constraint on the edge.
Let G = (V, E) be a flow network with flow f. The residual capacity of an augmenting path p is
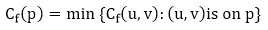
The residual capacity is the maximal amount of flow that can be pushed through the augmenting path. If there is an augmenting path, then each edge on it has a positive capacity. We will use this fact to compute a maximum flow in a flow network.
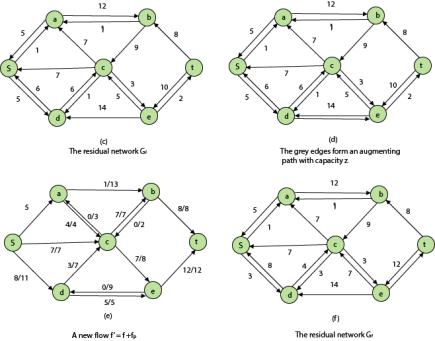
Key takeaways:
Definition: A Flow Network is a directed graph G = (V, E) such that
For each edge (u, v) ∈ E, we associate a nonnegative weight capacity c (u, v) ≥ 0. If (u, v) ∉ E, we assume that c (u, v) = 0.
4. There are two distinguishing points, the source s, and the sink t;
5. For every vertex v ∈ V, there is a path from s to t containing v.
Let G = (V, E) be a flow network. Let s be the source of the network, and let t be the sink. A flow in G is a real-valued function f: V x V→R such that the following properties hold:
References:
1. Introduction to Algorithms, 4TH Edition, Thomas H Cormen, Charles E Lieserson, Ronald L Rivest and Clifford Stein, MIT Press/McGraw-Hill.
2. Fundamentals of Algorithms – E. Horowitz et al.
3. Design and Analysis of Algorithms, M.R.Kabat, PHI Learning
4. Algorithm Design, 1ST Edition, Jon Kleinberg and ÉvaTardos, Pearson.
5. Algorithm Design: Foundations, Analysis, and Internet Examples, Second Edition, Michael T Goodrich and Roberto Tamassia, Wiley.
6. Algorithms—A Creative Approach, 3RD Edition, UdiManber, Addison-Wesley,
Reading, MA.