Unit - 4
Tractable and Intractable Problems
COMPUTABILITY Could the task be computed by an algorithm?
Is the assignment I want impossible?
A difficult mission can be conceived.
What are the implications for other algorithms?
Computability Vs Complexity
● Computability refers to whether it is possible to test f(n) by following a set of instructions, not in theory.
● For the moment, we are not worried whether 1,000,000 or more consecutive steps are required for this measurement.
● The above applies to the uncertainty we will later return to.
● The P class solves the problem of deterministic computation.
● P class is used to solve the problems that are solvable in polynomial run time.
● The problem belongs to class P if it’s easy to find a solution for the problem.
● This problem can be solved by the worst case in O(nK) where k is constant.
● The problems which are solved by P class are known as tractable problems and others are known as intractable or super polynomial.
● If polynomial time is P(n) then the algorithm can solve in time O (P(n)) with input size n.
● The advantage of the class of polynomial time algorithms is that all reasonable deterministic single processor models of computation can be simulated on each other with at most polynomial slow-d.
● The NP class solves the problem of non-deterministic computation.
● The problem belongs to NP, if it’s easy to check a solution that may have been very tedious to find.
● It solves the problem which is verifiable by polynomial time.
● It is a class of decision problems.
● For using this class, it is easy to check the correctness of the claimed answer even if it has extra information added in it.
● Hence it is used to verify the solution is correct, not for finding the solution.
● If there is a problem in this class then it can be solved by exhaustive search in exponential time.
● NP complete class is used to solve the problems of no polynomial time algorithm.
● If a polynomial time algorithm exists for any of these problems, all problems in NP would be polynomial time solvable. These problems are called NP-complete.
● The phenomenon of NP-completeness is important for both theoretical and practical reasons.
● Following are the no polynomial run time algorithm:
Application of NP complete class
● A clique is a complete sub graph which is made by given undirected graph.
● All the vertices are connected to each other i.e.one vertex of undirected graph is connected to all other vertices in graph.
● There is the computational problem in clique where we can find the maximum clique of graph this known as max clique.
● Max’s clique is used in many real-world problems and in many applications.
● Assume a social networking where peoples are the vertices and they all are connected to each other via mutual acquaintance that becomes edges in graph.
● In the above example clique represents a subset of people who know each other.
● We can find max clique by taking one system which inspect all subsets.
● But the brute force search is too time consuming for a network which has more than a few dozen vertices present in the graph.
Example:
● Let's take an example where 1, 2, 3, 4, 5, 6 are the vertices that are connected to each other in an undirected graph.
● Here subgraph contains 2,3,4,6 vertices which form a complete graph.
● Therefore, subgraph is a clique.
● As this is a complete subgraph of a given graph. So, it’s a 4-clique.
Analysis of Clique Algorithm
● Non-deterministic algorithms use max clique algorithms to solve problems.
● In this algorithm we first find all the vertices in the given graph.
● Then we check if the graph is complete or not i.e., all vertices should form a complete graph.
● The no polynomial time deterministic algorithm is used to solve this problem which is known as NP complete.
2. Vertex Cover
● A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.
● In a given undirected graph we need to find the maximum size of vertex cover.
● It is the optimization version of NP complete problems.
● It is easy to find vertex cover.
Example:
Given graph with set of edges are
{(1,6), (1,2), (1,4), (2,3), (2,4), (6,7), (4,7), (7,8), (3,8), (3,5), (8,5)}
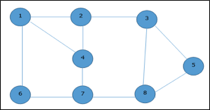
Now, start by selecting an edge (1, 6).
Eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1, 6) to cover.
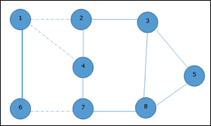
In the next step, we have chosen another edge (2, 3) at random
Now we select another edge (4, 7).
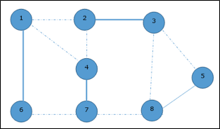
We select another edge (8, 5).
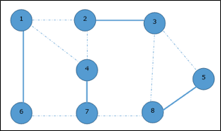
Hence, the vertex cover of this graph is {1, 2, 4, 5}.
Analysis of Vertex Cover Algorithm
● In this algorithm, by using an adjacency list to represent E it is easy to see the running time of this algorithm is O (V+E).
● A problem is in the class NPC if it is in NP and is as hard as any problem in NP.
● A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.
● The problem in NP-Hard cannot be solved in polynomial time, until P = NP.
● If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it.
● Instead, we can focus on design approximation algorithms.
● Following are the NP hard class problems:
In his paper "The Complexity of Theorem Proving Procedures," Stephen Cook proposed four theorems. Below are these theorems mentioned.
The four theorems by Stephen Cook follow:
If a set S of strings is accepted by some non-deterministic Turing machine within polynomial time, then S is P-reducible to {DNF tautologies}.
The following sets are P-reducible to each other in pairs (and hence each has the same polynomial degree of difficulty): {tautologies}, {DNF tautologies}, D3, {sub-graph pairs}.
● For any TQ(k) of type Q,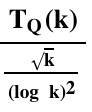 
is unbounded.
● There is a TQ(k) of type Q such that TQ (K) ≤ 2K (log K)2
Theorem-4
If the set S of strings is accepted by a non-deterministic machine within time T(n) = 2n, and if TQ(k) is an honest (i.e., real-time countable) function of type Q, then there is a constant K, so S can be recognized by a deterministic machine within time TQ(K8n).
● First, he emphasizes the importance of polynomial time reducibility. This implies that if we have a reduction in polynomial time from one problem to another, it guarantees that for the first problem, every polynomial time algorithm from the second problem can be translated into a corresponding polynomial time algorithm.
● Second, he centred attention on the class NP of decision problems that a non-deterministic machine can solve in polynomial time. This class, NP, belongs to most of the intractable issues.
● Third, he showed that one unique problem in NP has the property that it can be polynomially reduced to any other problem in NP. If a polynomial time algorithm can solve the satisfactoriness problem, then every problem in NP can also be solved in polynomial time. If any NP problem is intractable, then the problem of satisfaction must be intractable. Thus, in NP, the most difficult problem is the problem of satisfaction.
● Fourth, Cook suggested that NP's other issues could share this property of being the hardest member of NP with the satisfaction issue.
NP Completeness Benefits
A clique is a subgraph of a graph in which all of the vertices are bound to one another, making the subgraph a complete graph. The aim of the Maximal Clique Problem is to find the largest clique in a given graph G, which is a complete graph that is a subgraph of G that has the most vertices. This is a topic in optimization. The Clique Decision Problem, on the other hand, is to determine whether or not a clique of size k exists in the given graph.
If a problem belongs to the NP class, it should have polynomial-time verifiability, which means that given a credential, we should be able to check whether it is a solution to the problem in polynomial time
The Clique Decision Problem belongs to NP-Hard
If any NP problem can be reduced to L in polynomial time, the problem L is NP-Hard. Let's take a look at the Clique Decision Problem by C. To demonstrate that C is NP-Hard, we take an existing NP-Hard problem, such as S, and reduce it to C for a specific case. C is also an NP-Hard problem if this reduction can be achieved in polynomial time.
According to Cook's theorem, the Boolean Satisfiability Problem (S) is an NP-Complete problem. As a result, in polynomial time, any NP problem can be reduced to S. As a result, if S is polynomially reducible to C, any NP problem can be reduced to C in polynomial time, proving C to be NP-Hard.
References:
1. Introduction to Algorithms, 4TH Edition, Thomas H Cormen, Charles E Lieserson, Ronald L Rivest and Clifford Stein, MIT Press/McGraw-Hill.
2. Fundamentals of Algorithms – E. Horowitz et al.
3. Design and Analysis of Algorithms, M.R.Kabat, PHI Learning
4. Algorithm Design, 1ST Edition, Jon Kleinberg and ÉvaTardos, Pearson.
5. Algorithm Design: Foundations, Analysis, and Internet Examples, Second Edition, Michael T Goodrich and Roberto Tamassia, Wiley.
6. Algorithms—A Creative Approach, 3RD Edition, UdiManber, Addison-Wesley,
Reading, MA.
