Unit - 2
Relations and Functions
We define a relation in terms of ordered pairs-
An ordered pair of elements of x and y, where x is the first element and y is the second element, it is denoted by (x, y),
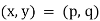
If and only if x = p and y = q
Thus (x, y)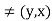
unless x = y
Product sets-
Suppose we have two sets X and Y. the set of all ordered pairs (x, y) where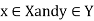 
is called the Cartesian product of X and Y.
It is represented as follows-
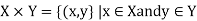
And it is read as X cross Y.
Relation-
Let X and Y are two sets, A relation from X to Y is a subset of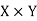 
.
Now suppose R is a relation form X to Y, then R is a set of ordered pairs where each first element comes from X and each second element comes from Y.
For each pair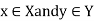 
, one the following rule is true-
1. 
2.
The domain of a relation R is the set of all first elements of the ordered pairs which belongs to R, and range is the second element.
Pictorial representation of relations-
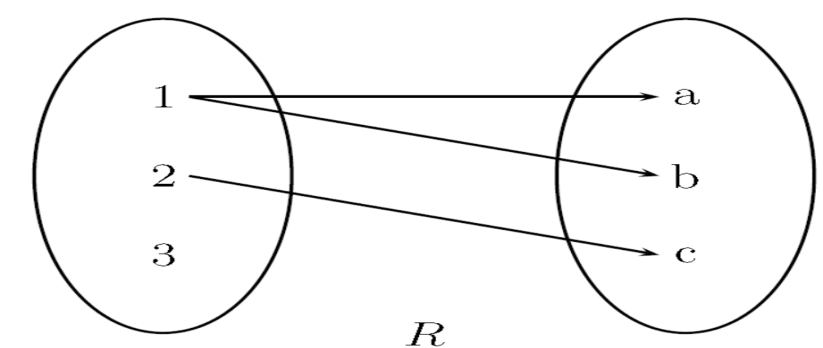
Let A = {1, 2, 3}, B = {a, b, c} and R = {(1, a), (1, b), (2, c)}
Then this relation can be represented as in picture format-
Inverse relation-
Let R be any relation from set X to set Y. the inverse of R is the relation form Y o X which consists of those ordered pairs which, when reversed, belong to R, such that-
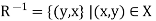
Example- If R = {(1, x), (1, y), (2, z)} then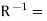 
{(x, 1), (y, 1), (z, 2)}
Composition of relations-
Let X, Y and Z are three sets and R be a relation from X to Y and S is a relation from Y to Z.
So that R is a subset of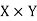 
and S is a subset of 
.
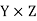Then R and S give a relation form X to Z which is denoted by RoS,
And can be defined as follows-
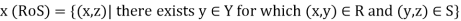
The relation RoS is called the composition of R and S.
Note- If R is a relation on a set A, that is, R is a relation from a set A to itself. Then the composition of R is RoR. Denoted by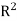 
.
Types of relations-
1. Reflexive relations
A relation R on a set X is reflexive if xRx for every x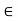
X. that is is (x, x)
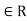for every x
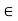X. thus R is not reflexive if there exists x
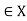such that (x, x) does not belongs to R.
2. Symmetric and anti-symmetric relations-
A relation R on a set X is said to be symmetric if whenever xRy then yRx, that is if whenever (x, y) ∈R then (y, x) ∈R
R is said to be anti-symmetric if (x, y) ∈X such that (x, y) ∈R but (y, x)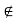
R
3. Transitive relation-
A relation R on a set X is said to be transitive if whenever xRy and yRz then xRz, that is, if whenever (x, y), (y, z) ∈R then (x, z) ∈R
Equivalence relation-
A relation in a set R is said to be an equivalence relation in A, If R is reflexive, symmetric and transitive.
Irreflexive relation
A relation R on a set A is irreflexive if aRa for every a ∈A
Example-
Let A = {1, 2, 3} and
R = {(1, 2), (2, 3), (3, 1), (2, 1)}
Then the relation R is irreflexive on A.
Asymmetric relation-
A relation R defined on a set A is asymmetric if whenever aRb, then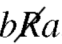 
.
Example:
Let A = {a, b, c} and R = {(a, b), (b, c)} be a relation on A. then R is a symmetric.
Compatible relation-
A relation R in A is said to be a compatible relation if it is reflexive and symmetric.
If R is an equivalence relation on A, then R is compatible relation on A.
Universal relation-
A relation R in a set A is said to be universal relation if
R = A × A
Example:
Let A = {1, 2, 3}, then
R = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
is a universal relation on A.
Complementary relation-
Let R be a relation from A to B, then the complement of R denoted by R′ and is
Expressed in terms of R as follows;
aRb if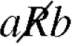 
The inverse of a relation-
Let R be a relation from A to B. Then the relation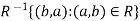 
from B to A is called the inverse of R.
Example-1: A = {2, 3}, B = {3, 4, 5, 6} and R is a relation from A to B defined as follows-
(a, b) ∈R if “a divides b” write the solution set of R.
Sol: 2 divides 4 and 2 divides 6
⇒ (2, 4) ∈R and (2, 6) ∈R
3 divides 3, 3 divides 6
⇒ (3, 3) ∈R and (3, 6) ∈R
4 divides 4 ⇒ (4, 4) ∈R
Thus R = {(2, 4), (2, 6), (3, 3), (3, 6), (4, 4)}
Example-2: Let Z denote the set of integers and the relation R in Z be defined by “aRb” iff a – b is an even integer”. Then show that R is an equivalence relation.
Sol.
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Key takeaways-
3. A relation R on a set X is reflexive if xRx for every x
X. that is is (x, x)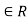
for every x
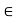X. thus R is not reflexive if there exists x
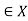such that (x, x) does not belongs to R.
4. A relation R on a set X is said to be transitive if whenever xRy and yRz then xRz, that is, if whenever (x, y), (y, z) ∈R then (x, z) ∈R
5. A relation R defined on a set A is asymmetric if whenever aRb, then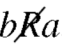 
.
Let R be a relation on the set A.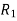 
denote the transitive extension of R, 
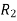denote the transitive extension of 
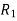and in general 
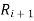denote the transitive extension of 
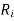then the transitive closure of R is defined as the set union of R, 
,
,
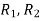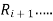It is denoted by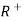 
Thus
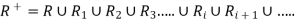
Example: Let A = {1, 2, 3, 4} and B = {a, b, c, d, e, f} consider the relation
R = {(1, a), (1, c), (1, e), (2, b), (2, d), (2, f), (3, c), (3, d), (4, a), (4, f)}
Let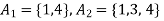 
then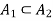 
And
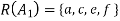
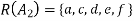
Clearly-
Thus,
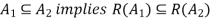
Warshall’s algorithm is used to find the transitive closure of a relation. It is considered to be the best method which is described below-
Let X= {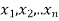
} and R is the relation on X. If 
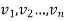is a path in R, then the Vertices 
,
...,
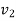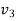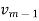are said to be internal vertices.
For 1 ≤r ≤n we define a Boolean matrix,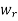 
as follows:
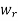has a 1 in position i, j if there is a path from 
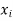to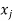 
in R whose internal vertices if any are the members of the set {
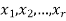}. Since all the vertices of the diagram are the elements of A, this follows that 
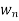has a 1 is position i, j if and only if some path in R connects 
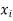with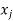 
. If we define 
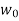tobe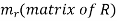 
then we will have a sequence 
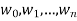where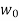 
= 
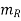and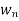 
=
.
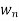Suppose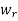 
= [
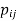] and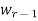 
= [
].
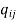If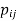 
= 1, then there must be a path from 
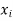to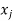 
whose interior vertices belong to the set {
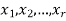}. If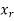 
is not an interior vertex of this path, then all the interior vertices must come from the set {
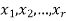}. such that 
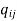= 1.
Hence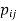 
= 1 iff
(i)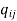 
= 1 or
(ii)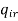 
= 1 and 
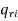= 1
If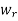 
– 1 has a 1 in position 
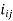then the matrix 
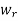and, a new 1 can be added in
Position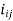 
of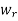 
if and only if rth column of 
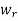– 1 has a 1 in position i. The following steps are involved in computing 
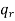from 
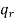– 1.
Step 1: Transfer all 1’s in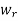 
–1 to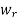 
Step 2: List the locations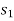 
, 
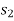, ... in column r of 
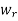–1 where the entry is 1 and the locations 
, 
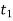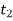, ..., in row r of 
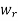–1 where the entry is 1.
Step 3: Put 1’s in all the positions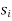 
, 
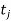of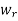 
(if there are 1’s in such positions).
Definition-
A relation R in a set A is said to be an equivalence relation in A, if R is reflexive, symmetric and transitive.
Example- Let A = {a, b, c}, and R = {(a, a), (a, b), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)} then R is an equivalence relation in A.
Example: Let Z denote the set of integers and the relation R in Z be defined by “aRb” iff a – b is an even integer”. Then show that R is an equivalence relation.
Sol.
1. R is reflexive; since
∅ = a −a is even, hence aRa for every a∈Z.
2. R is symmetric:
If a – b is even then b – a = – (a – b) is also even hence aRb⇒bRa
3. R is transitive: for if aRb and bRc then both a – b and b – c are even.
Consequently, a – c = (a – b) + (b – c) is also even.
∴aRb and bRc⇒aR c
Thus, R is an equivalence relation.
Key takeaways-
A relation R in a set A is said to be an equivalence relation in A, if R is reflexive, symmetric and transitive.
Partial orderings-
A relation R on a set Sis called a partial order relation in Sif R is, Reflexive Anti-symmetric and transitive.
A set S together with a partial ordering R is called a partially ordered set.
We denote a partial order relation by the symbol ≤.
Comparability-
Suppose R be a partial order on Sand a, b ∈S whenever aRb or bRa, we say that a A a and b are comparable otherwise a And b are non-comparable.
Dual order-
If ≤is a partial order on a set S, then the converse of R is also a partial order on S. that means if ≤is a partial ordering on S, then ≥is also a partial ordering on S. (S, ≥) is called the dual of (S, ≤).
Partitions-
Let S be a set which is non-empty. Then the collection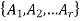 
of subset of S is said to be a partition of S if-
1. 
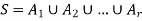
2. For any 
Either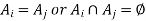 
Cross partition-
If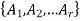 
and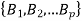 
both are partition of set S which is non-empty, then 
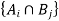forms a partition of S
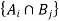is called a cross partition of S.
Ordered partition-
A partition a non-empty set is called an ordered partition of S if there is a specified order on the subsets of S.
An ordered t-tuple of sets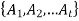 
is called a t-part ordered partition if the sets 
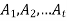form a partition of S.
Theorem-
The number ‘m’ of ordered partitions of a set S with ‘n’ elements into r cells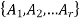 
, where for each ‘i’, n (
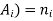– follows-
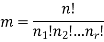
Example:
Find the number of ways to partition of 10 peoples into four groups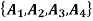 
So that two teams contain 3 persons and two teams contain 2 persons.
Sol.
By using above theorem, we get-
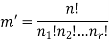
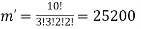ordered partitions
Here the group form an unordered partition so that we divide m’ by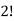 
Because of the two cells with three elements each and 
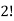Because of the two cells with two elements each.
So that-
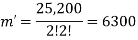
Example: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total -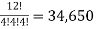 
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Hasse Diagram-
The elements in Hasse diagram are represented as vertices and it is pictorial representation of a finite order on a set.
Two related vertices of a partial order are connected by line if they are related.
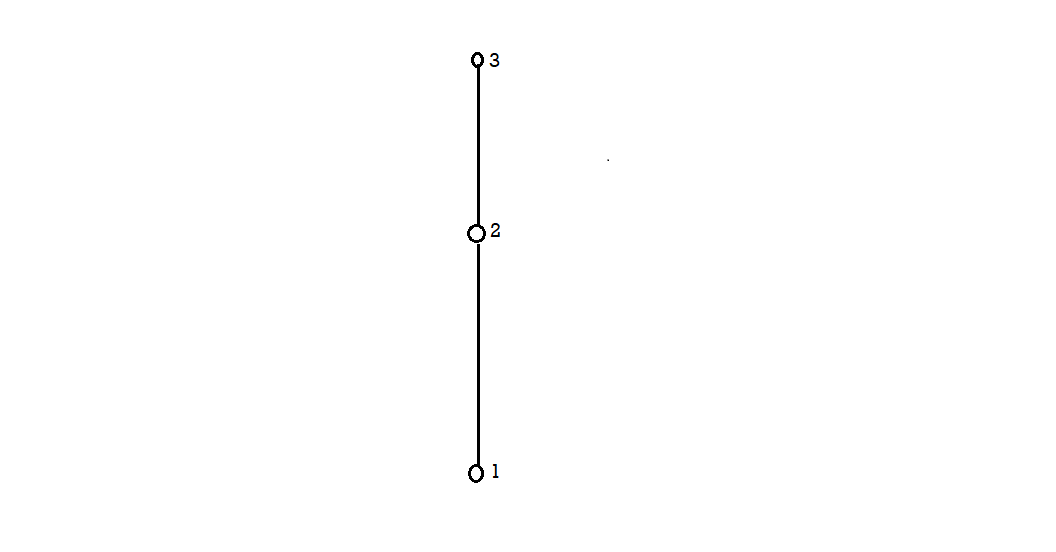
Example-1: If A = {1, 2, 3} and ≤ be a relation on A. the Hasse diagram will be-
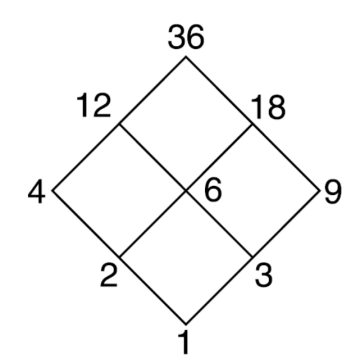
Example-2: Draw the Hasse diagram of positive division of 36.
Sol.
We have
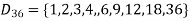
Suppose R is the partial order relation on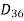 
The Hasse diagram will be-
Example-3: Let B = {a, b, c, d, e} then the Hasse diagram defines a partial order on B in the natural way. That is, d ≤ b, d ≤ a, e ≤ c and so on.
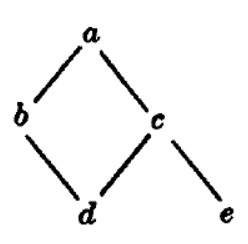
Key takeaways-
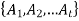
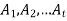
Lattices-
A lattice is a partially ordered set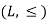 
in which every pair of elements a, b
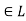has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S);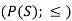 
that means (
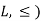is partially ordered.
If X and Y are two elements of L, then-
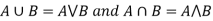
Hence (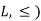
is a Lattice.
Axiomatic definition of Lattice-
Let L be a non-empty set closed under two binary operations denoted by ∧ and ∨.
Then L is said to be a Lattice if it follows the axioms given below, here a, b and c are the elements of L.
1. Commutative law-
(i) a∧b = b∧a (ii) a∨b = b∨a
2. Associative law-
(i) (a∧b) ∧ c = a∧(b∧c) (ii) (a∨b) ∨ c = a∨ (b∨c)
3. Absorption law-
(i) a∧ (a∨b) = a (ii) a∨(a∧b) = a
To show that which operation is involved we denote the Lattice by (L, ∧, ∨)
Theorem-Let (L, ≤) be a lattice in which ‘⋅’ And ‘+’ denote the operations of meet and join respectively.
Then
a≤b⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
Proof: Suppose a ≤b
As we know that a ≤a so that a ≤a. b but according to definition a. b≤a
So that- a ≤b ⇒a ⋅b = a
Let a ⋅b = a
But this is possible only if a ≤b which means a ⋅b = a ⇒a ≤b
∴a≤b⇒a⋅b = a and a ⋅b = a ⇒a ≤b
Combine these two, we get
a≤b⇔a ⋅b = a
Now let,
a⋅b= a,
Then we have
b + (a ⋅b) = b + a + a + b
But,
b + (a ⋅b) = b
Hence a + b = b
Similarly, by assuming a + b = b
We can show that a ⋅b = a
Hence a ≤b ⇔a ⋅b = a ⇔a + b = b = a
Isomorphic Lattice-
Two lattices L and L’ are said to be isomorphic if there is a one-to-one correspondence
f: L →L’
Such that
f (a ∧b) = f (a) ∧f (b) and f (a ∨b) = f (a) ∨f (b)
For any elements a, b in L.
Note-
1. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
2. A lattice L is complemented if it is bounded and if every element in L has a complement.
3. Let (L, ⋅, +, 0, 1) be a bounded lattice and a ∈L. If there exists an element b ∈L
Such that
a⋅b= 0 and a + b = 1
Then b is called the complement of a.
Sub Lattices and Direct products-
Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sub lattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sub lattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and 2 (L, ∧, ∨) be two lattices. The algebraic system (L1 × L2, +)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅ (a2, b2) = (a1 ∗a2, b1 ∧b2)
(a1, b1) + (a2, b2) = (a1 ⊕a2, b1 ∨b2)
For all (a1, b1) and (a2, b2) (a2, b2) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Note-
1. Let (L, ⋅, +, 0, 1) be a lattice L is said to complemented lattice if every element has at least one complement.
2. A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
3. Let (L, ≤) be a lattice, with an upper bound 1. An element a ∈L is said to be meet irreducible if a = x ⋅y implies a = x or a = y.
If a ≠0 then a is meet irreducible if and only if a has unique immediate successor
Chain-
Let (A, ≤) be a partially order set. If for every a, b ∈A, we have a ≤b or b ≤a,
Then ≤is called a simple ordering (or linear ordering) on A, and the set (A, ≤) is
Called a chain.
Chain is also called totally ordered set.
Key takeaways-
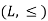
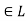
Then
a≤b⇔a ⋅b = a ⇔a + b = b ∀a, b, c ∈L
3. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
4. A lattice L is complemented if it is bounded and if every element in L has a complement.
5. Let (L, ≤) be a lattice. A non-empty subset A of L is called a sub lattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
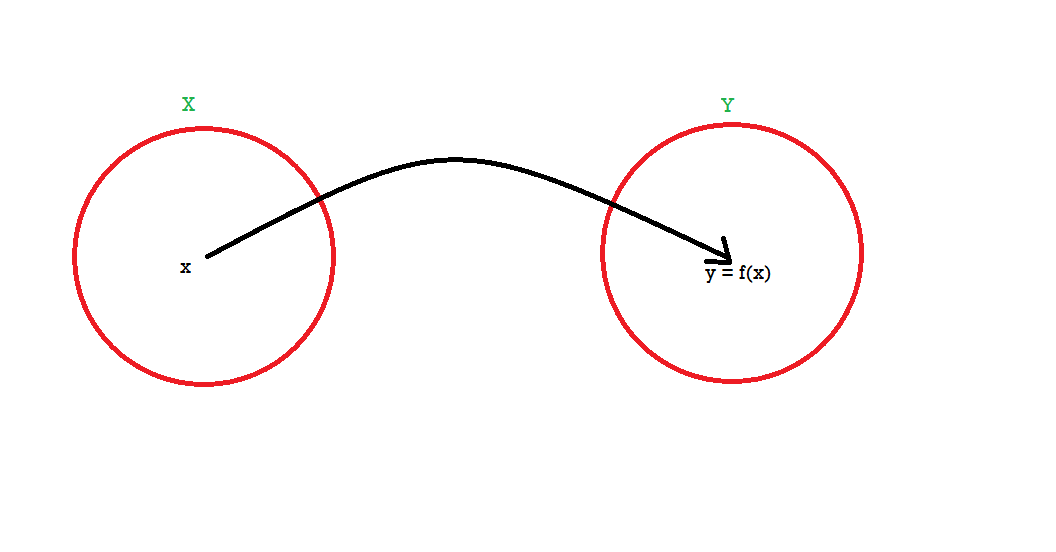
Let X and Y are two sets. A relation f from X to Y is said to be a function if for every x ∈ X there is a unique element y ∈ Y, such that (x, y) ∈ X
We denote it as f: X → Y, which means f is a function from X to Y.
We represent the function as-
Example: Let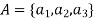 
and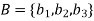 
And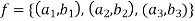 
Hence the function can be represented as-
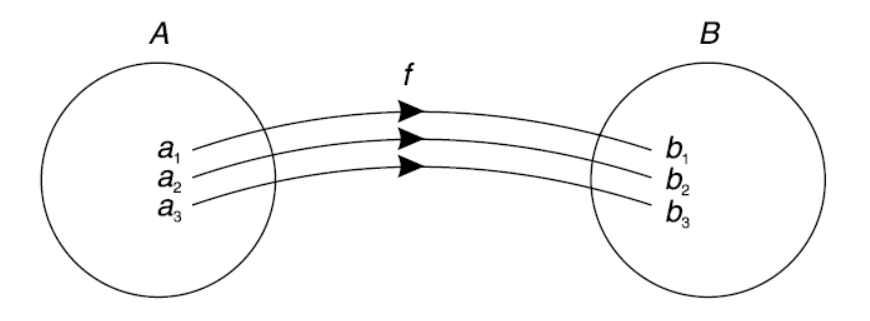
Here A is called the domain of f and B is called the co-domain of f
Surjective function (Onto-Mapping)-
A mapping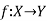 
is said to be onto-mapping if the range set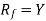 
If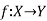 
is onto then each element of B if f-image of at least one element of X.
That means.
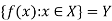
A mapping is said to be into if it is not onto.
Injective function (One-To-One Mapping)-
A mapping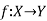 
is said to be one-to-one mapping if distinct elements of X are mapped into distinct elements of Y.
That means if f is a one-to-one mapping, then-
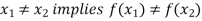
Or
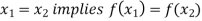
Bijective functions (One-To-One, Onto)-
A mapping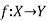 
is said to be bijective mapping if it is both one-to-one and onto.
Identity function (Identity Mapping)-
If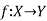 
is a function such that every element of X is mapped onto itself then f is said to be an identity mapping.
We denote identity mapping by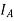 
.
If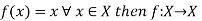 
is an identity mapping.
Partial functions-
Let X and Y be sets and A be a subset of X. A function f from A to Y is called a partial function from X to Y. The set A is a called the domain of f.
Constant function-
Let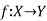 
then f is said to be a constant function if every element of X is mapped onto the same element of Y.
Inverse functions-
Let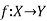 
is a one-one and onto mapping, then 
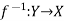is called the inverse mapping of f.
Inverse mapping can be defined as-
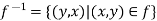
Example-1: Prove that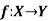 
is both one-one and onto then 
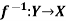is both one-one and onto.
Sol.
Let f: X→Y be both one-one and onto.
Then there exist elements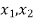 
∈X, and elements
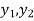∈Y
Such that
f (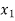
) = 
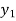, and f (
) =
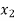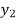
Or
= 
(
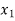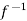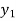) and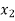 
= 
(
)
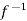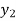Now,
Let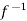 
(
) =
(
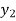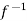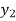), then
(
) =
(
)
⇒
= 
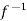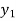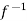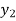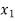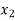
⇒f (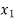
) = f (
)
⇒
= 
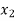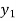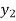
Thus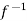 
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x=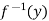 
So that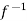 
is onto.
Hence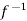 
is both one-one and onto.
Key takeaways
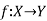
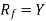
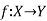
Let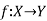 
and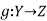
are two mappings, then the composition of these two mappings f and g is denoted by gof is the mapping from X into Z.
It is defined as-
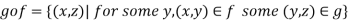
That means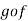 
is a mapping defined as below-
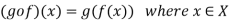
Example-1: Show that the inverse of an invertible mapping is unique.
Sol
Let 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
are two different inverse mapping of f.
Let y ∈ Y and
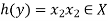
Now-
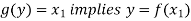
And
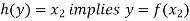
so that-
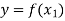and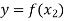
Now-
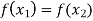
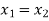
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Example-2: Prove that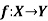 
is both one-one and onto then 
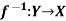is both one-one and onto.
Sol.
Let f: X→Y be both one-one and onto.
Then there exist elements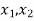 
∈X, and elements
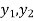∈Y
Such that
f (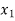
) = 
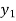, and f (
) =
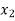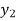
Or
= 
(
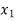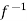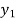) and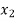 
= 
(
)
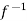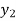Now,
Let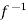 
(
) =
(
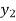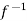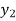), then
(
) =
(
)
⇒
= 
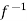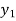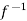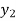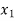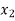
⇒f (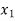
) = f (
)
⇒
= 
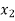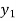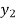
Thus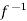 
is one-one
Since f is onto, for y∈Y, there is some element x∈X, such that f (x) = y.
Now
f(x) = y
⇒x=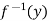 
So that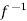 
is onto.
Hence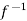 
is both one-one and onto.
Invertible function-
A function f from a set X to a set Y is said to be an invertible function if there exists a function g from Y to X, such that-
f(g(y)) = y
And
g(f(x)) = x
For every x ∈ X and y∈ Y
Example-1: Show that the inverse of an invertible mapping is unique.
Sol
Let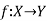 
By any invertible mapping,
Let,
g: Y→X
h: Y→X
are two different inverse mapping of f.
Let y ∈ Y and
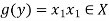
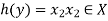
Now-
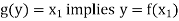
And
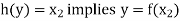
so that-
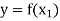and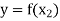
Now-
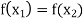
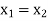
Which shows that g(y) = h(y)∀ y ∈ Y
So that the inverse of f is unique.
Recursive Functions
Definition-
A function f is said to be Primitive recursive if it can be obtained from the initial functions by a finite number of operations of composition and recursion.
Example: Show that addition is primitive recursive.
Sol.
Addition is defined by a + 0 = a, a + (b + 1) = (a + b) + 1 for all-natural numbers a, b.
We define f (a, b) = a + b such that
f (a, b + 1) = a + b + 1 = (a + b) + 1
= f (a, b) + 1
= S (f (a, b))
Also, f (a, 0) = a
We define f (a, b) as
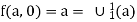
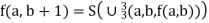
If follows that f comes from primitive recursion from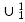 
and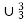 
so that f is primitive recursive.
Key takeaways
f(g(y)) = y
And
g(f(x)) = x
For every x ∈ X and y∈ Y
2. A function f is said to be Primitive recursive if it can be obtained from the initial functions by a finite number of operations of composition and recursion.
Pigeonhole principle (statement)-
If n pigeonholes are occupied by n + 1 or more pigeons, then at least one pigeonhole is occupied by more than one pigeon.
Example-1: Suppose a class contains 13 students, then two of the students (pigeons) were born in the same months (pigeonholes)
Example-2: Show that if seven numbers from 1 to 12 are chosen, then two of them will add up to 13.
Sol.
First, we will construct six different sets, each containing two numbers that add up to 13 as follows-
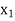= {1, 12}, 
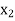= {2, 11}, 
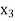= {3, 10}, 
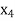= {4, 9}, 
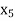= {5, 8}, 
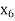= {6, 7}.
Each of the seven numbers belong to one of these six sets.
Since there are six sets, then according to the pigeonhole principle that two of the numbers chosen belong to the same set. These numbers add up to 13.
Generalized pigeonhole principle-
If n pigeonholes are occupied by kn+ 1 or more pigeons, where k is a positive integer, then at least one pigeonhole is occupied by k + 1 or more pigeons.
Example- Find the minimum number of persons in a group that three of them are born in the same month.
Sol.
Here the n = 12 months are the pigeonholes, and k + 1 = 3 so k = 2. Hence among any kn+ 1 = 25 students (pigeons), three of them are born in the same month.
Key takeaways
References:
