Unit - 3

Numeric Functions and Generating Functions

3.1 Discrete Numeric functions

All those functions whose domain is the set of natural numbers and whose range is the set of real numbers are called numeric function.

We use bold face lowercase letters to denote Numeric functions.

For example:

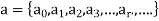
Is the numeric function where 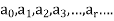denotes the values a at 0,1,2, 3…...r……

Note-

If a and b denote two numeric functions then their sum and product are also numeric functions. If k is a scalar and a is a numeric function. The k is also numeric function.

Forward and backward differences-

If

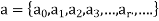
Then 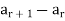is called its forward difference at r.

We denote it by .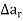

The backward difference is denoted by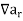

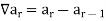
The convolution of two numeric function a and b is a numeric function c such that-

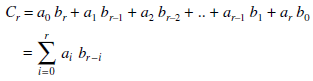
We denote the convolution of a and b by a * b

Asymptomatic behavior of numeric function-

Suppose a is a numeric function, then the meaning of asymptomatic behavior is that how the volume of the function a varies for large r.

Key takeaways

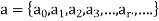
Then 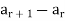is called its forward difference at r.

4.     The backward difference is denoted by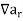

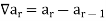
3.2 Generating Functions

For a numeric function-

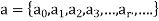
An infinite series is defined as-

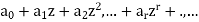 which is called the generating function of a.

We denote it by A(Z).

The coefficient of 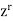is A (z) is the value of the numeric function a.

For example:

If the generating function is

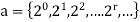
is

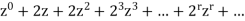
We can write the above series as below-

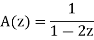
In 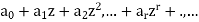  the term 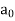is called the constant term.

Let

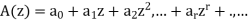
And

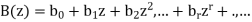
Are the generating functions.

A(z) and B(z) are equal if 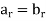, for each

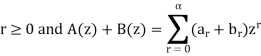
The product can be defined as-

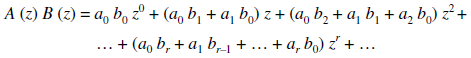
Note-

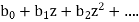
2.     the exponential generating function (egf) is the formal power series

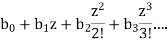
3.     If the sequence has finitely many elements, then the generating functions have finitely many terms.

3.3 Recurrence Relations and Recursive Algorithms

Recursion is a technique of defining a function, a set or an algorithm in terms of itself.

Suppose the set of natural numbers, we introduce the method of generating the set of natural numbers by recursion.

The natural numbers with zero are those objects which can be generated by starting with an initial object 0 and from any object “n” already generated passing to another uniquely determined object 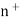, the successor of n. The objects differently generated are always distinct. Thus, the natural numbers appear as a set of objects 0,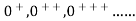

The transition to the usual notation is made upon introducing 1, 2, 3, 4, … to stand for 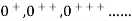and then employing the notation.

 The recursive formula for defining a sequence (or numeric function) is called a recurrence relation.

A recurrence relation is also called a difference equation.

The information accompanying a recursive formula about the beginning of the numeric function is called initial condition.

Example: Find a recurrence relation and initial conditions for 1, 5, 17, 53, 161, 485.

Sol.

Here 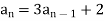is the recurrence relation and the initial condition is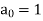

Example: Check whether 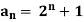is a solution to the recurrence relation 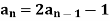with .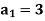

Sol.

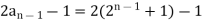
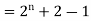
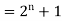
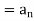
Key takeaways

3.4 Linear recurrence relations with constant coefficients

Suppose r and k are non-negative integers. A recurrence relation of the form

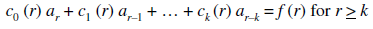
Here 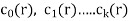and f(r) are the functions of r is said to be a recurrence relation.

If 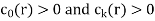 then it said to be a linear recurrence relation of degree k.

Linear recurrence relation with constant coefficient-

If 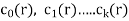are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.

A linear kth-order recurrence relation with constant coefficients is a recurrence relation of the form

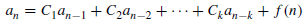
Where 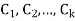are constant with 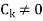and f(n) is a function of ’n’.

Example: Consider a following recurrence relation-

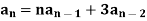
Sol.

It is a homogeneous linear second-order recurrence relation but it does not have constant coefficients because the coefficient of 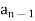is not a constant given initial conditions 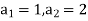, the next elements of the sequence follow-

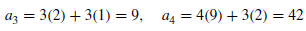
Note-

if follow f (r) = 0, then the recurrence relation is called a linear homogenous relation.

For example:

The following relations are linear recurrence relations with constant coefficients-

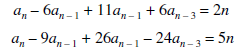
Key takeaways

If

are constants then the recurrence relation is called a linear recurrence relation with constant coefficients.

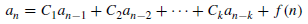
Where 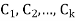are constant with 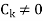and f(n) is a function of ’n’.

3.5 Solution of recurrence relations by the method of generating functions

Any numeric function that can be described by a recurrence relation together with an appropriate set of boundary conditions is called a solution of the recurrence relation.

If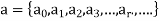
 

is a solution to a recurrence relation then it is said to satisfy the relation.

A given recurrence relation may or may not have a solution.

Method of generating functions-

Recurrence relations can also be solved by using generating functions. Some equivalent expressions used are given below-

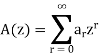
Then

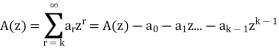
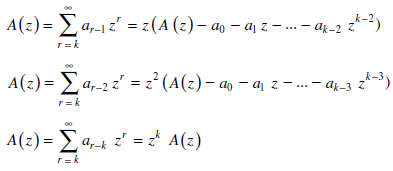
Example:  Solve the recurrence relation-

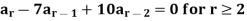
Sol.

Multiplying each term of the recurrence relation by 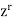, we find-

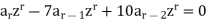
Now taking the sum to 2 to 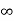, we get

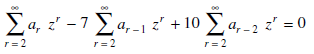
Replace each infinite sum by the corresponding equivalent expression given above, we obtain-

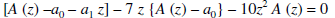
On simplifying, we obtain-

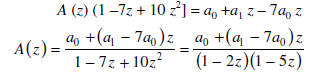
Decomposing A (z) as a sum of partial fractions, we can write

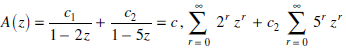
The solution is-

3.6 Divide and conquer algorithms

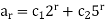
We divide this into three parts-

Divide/break- This includes the dividing the problem into some smaller sub problems and each problem solved independently  

Conquer/solve- Sub problem by calling recursively until sub problem solved.

Combine/merge- The sub problem solved and we get solution of the problem.

Let’s understand the by the following problem-

Here we will sort an array by using the divide and conquer approach-

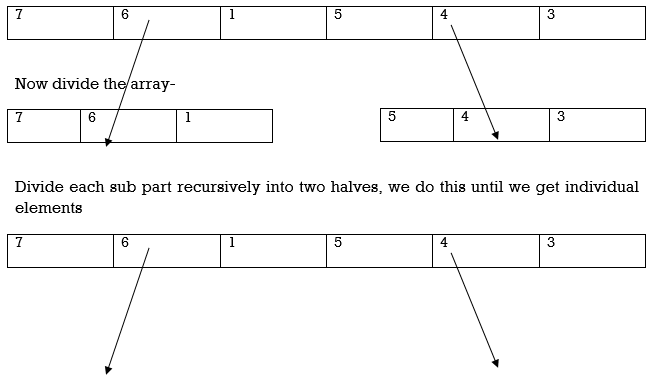
Now divide the array-

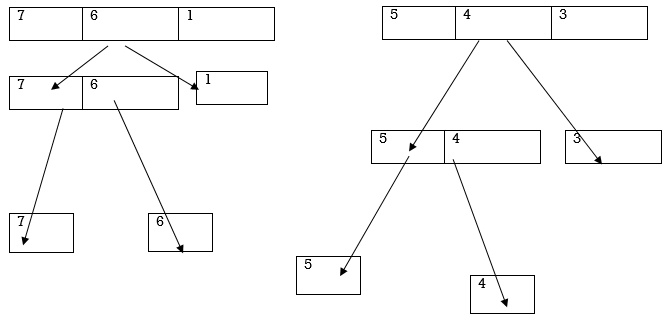
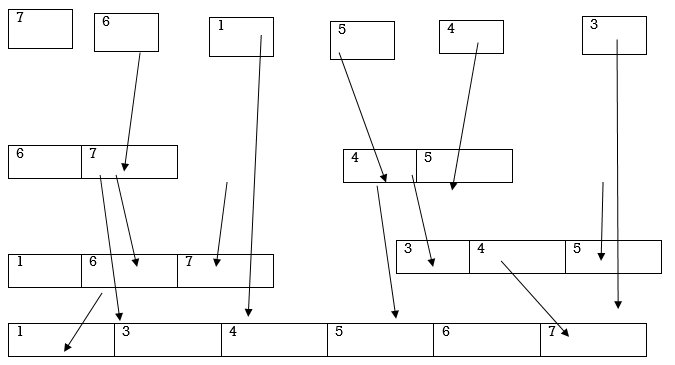
Combine the individual element in sorted way

Key takeaways

References: