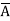Unit - 4
Groups and Rings
A group is an algebraic structure (G, *) in which the binary operation * on G satisfies the following conditions:
Condition-1: For all a, b, c, ∈ G
a* (b * c) = (a * b) * c (associativity)
Condition-2: There exists an elements e ∈G such that for any a ∈G
a* e= e * a = a (existence of identity)
Condition-3: For every a ∈G, there exists an element denoted by 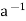 in G such that
in G such that
a* 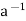 =
= 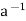 * a = e
* a = e
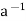 is called the inverse of a in G.
is called the inverse of a in G.
Example: (Z, +) is a group where Z denote the set of integers.
Example: (R, +) is a group where R denote the set of real numbers.
Abelian group-
Let (G, *) be a group. If * is commutative that is
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
Finite group-
A group G is said to be a finite group if the set G is a finite set.
Infinite group-
A group G, which is not finite is called an infinite group.
Order of a finite group-
The order of a finite group (G, *) is the number of distinct elements in G. The order of
G is denoted by O (G) or by |G|.
Example: If G = {1, -1, i, -i} where i = 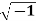 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First, we will construct a composition table-
. | 1 | -1 | i | -i |
1 | 1 | -1 | i | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | I | 1 | -1 |
It is clear from the above table that algebraic structure (G,.) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅ (b ⋅c)
Since
1 ⋅ (−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅ (−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties hold.
∴ Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅ (−1) = 1 = (−1) ⋅ (−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus, all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied.
Hence (G, ⋅) is an abelian group.
Example-
Prove that the set Z of all integers with binary operation * defined by a * b = a + b + 1 ∀a, b ∈G is an abelian group.
Sol: Sum of two integers is again an integer; therefore a +b ∈Z ∀a, b ∈Z
⇒a +b + 1 ⋅∈Z ∀a, b ∈Z
⇒Z is called with respect to *
Associative law for all a, b, a, b ∈G we have (a * b) * c = a * (b * c) as
(a* b) * c = (a + b + 1) * c
= a + b + 1 + c + 1
= a + b + c + 2
Also
a* (b * c) = a * (b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
Hence (a * b) * c = a * (b * c) ∈a, b ∈Z.
Key takeaways-
a* b = b * a for all a, b ∈G then (G, *) is called an Abelian group.
2. A group G is said to be a finite group if the set G is a finite set.
3. The order of a finite group (G, *) is the number of distinct elements in G. The order of G is denoted by O (G) or by |G|.
Subgroup
Let (G, *) be a group and H, be a non-empty subset of G. If (H, *) is itself is a group, then (H, *) is called sub-group of (G, *).
Example-Let a = {1, –1, i, –i} and H = {1, –1}
G and H are groups with respect to the binary operation, multiplication.
H is a subset of G, therefore (H, X) is a sub-group (G, X).
Theorem-
If (G, *) is a group and H ≤G, then (H, *) is a sub-group of (G, *) if and only if
(i) a, b ∈H ⇒a * b ∈H;
(ii) a ∈ H ⇒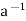 ∈H
∈H
Proof:
If (H, *) is a sub-group of (G, *), then both the conditions are obviously satisfied.
We, therefore prove now that if conditions (i) and (ii) are satisfied then (H, *) is a sub-group of (G, *).
To prove that (H, *) is a sub-group of (G, *) all that we are required to prove is: * is associative in
H and identity e ∈ H.
That * is associative in H follows from the fact that * is associative in G.
Also,
A ∈ H ⇒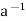 ∈H by (ii) and e ∈H and
∈H by (ii) and e ∈H and 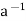 ∈H ⇒a *
∈H ⇒a * 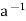 = e ∈H by (i)
= e ∈H by (i)
Hence, H is a sub-group of G.
Cosets-
Let (H, *) be a sub-group (G, *) and a ∈G
Then the sub-set:
a* H = {a * h: h ∈H}is called a left coset of H in G, and the subset
H * G = {h * a: h ∈H}is called a right coset of H in G.
Theorem: If (H, *) is a sub-group (G, *), then a * H = H if and only if a ∈H.
Proof: Let a * H = H
Since e ∈H then a = a * e ∈a * H
Hence a ∈H
Conversely
Let a ∈H then a * H ⊆H
(H, *) is a sub-group.
∴a ∈ H, h ∈ H ⇒ 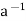 * h ∈ H.
* h ∈ H.
Now h ∈H
⇒h = a * (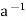 * h) ∈a * H
* h) ∈a * H
∴h ∈ H ⇒h ∈a * H
⇒H ⊆ a * H
Hence a * H = H
Homomorphism-
Let (G, *) and (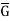 ,
,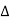 ) be any two groups. A mapping f: G →
) be any two groups. A mapping f: G →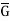 is called ahomomorphism of G to
is called ahomomorphism of G to 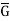 if.
if.
f (a * b) = f (a) 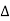 f (b) ∀a, b ∈G
f (b) ∀a, b ∈G
Example: Let G = R, the set of real numbers and 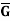 = R – {u)
= R – {u)
(G, +) and (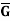 , ⋅) are groups. Define a mapping f: G →G by
, ⋅) are groups. Define a mapping f: G →G by
f(a) = 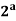 ∀a ∈G
∀a ∈G
Clearly f (a + b) = 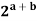 =
= 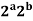 = f (a) ⋅f (b)
= f (a) ⋅f (b)
⇒f is a homomorphism of G into G.
Kernel of homomorphism-
Let G and G be any two groups and f: G →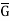 be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) =
be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = 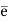 ).
).
Where e is the identity of 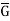 .
.
Example: Let G be (Z, +) i.e., the group of integers under addition and let f: G → G defined by
∅(x) = 3x ∀x ∈G. Prove that f is homomorphism, determine its Kernel.
Solution: We have ∅(x) = 3x ∀x ∈G
∀x, y ∈G ⇒x + y ∈G (∴G is a group under addition)
Now
f (x + y) = 3 (x + y)
= 3x + 3y
= f (x) + f (y)
Hence f is homomorphism.
Kernel of homomorphism consists of half of zero i.e., the integers whose double is zero.
Thus K = {0}
Key takeaways
Then the sub-set:
a* H = {a * h: h ∈H}is called a left coset of H in G, and the subset
H * G = {h * a: h ∈H}is called a right coset of H in G.
3. Let G and G be any two groups and f: G →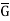 be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) =
be a homomorphism. Then Kernel of f denoted by Ker f the set K = (a ∈G: f (a) = 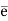 ).
).
Where e is the identity of 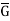 .
.
A word is a sequence of letters carrying some meaning. Suppose we decide to send a message in terms of 0 and 1 by using code.
A | by | 00 |
B | by | 01 |
C | by | 10 |
D | by | 11 |
Then the word ‘cad’ can be written as “100011”.
Encoding Function:
If an integers n>m and if there is one to one correspondence e: Bm Bn then e is called an (m, n) encoding function. In this way every word in Bm is represented b y a words in Bn.
Group codes:
An (m, n) coding function
E: Bm Bn is called a group code if
E(Bm) = {e(b)/ b EBM}
= Range (e)
Q.1) Show that (2, 5) encoding function e B2 B5 defined by
e (00) = 00000 e(10) = 10101
e (01) = 01110 e(11) = 11011
is a group code.
Let N = {00000, 01110, 10101, 11011}
We have that N is a sub group of B5
We shall prepare table for B5
0 + 0 = 0 0 + 1 = 1 1 + 0 = 0 1 + 1 = 0
e.g., 11011+01110=10101.
+ | 00000 | 01110 | 10101 | 11011 |
00000 | 00000 | 01110 | 10101 | 11011 |
01110 | 01110 | 00000 | 11011 | 10101 |
10101 | 10101 | 11011 | 00000 | 01110 |
11011 | 11011 | 10101 | 01110 | 00000 |
From the diagonal element true see that identity (00000) of B5 is N.
x, y belongs to N then n + y also belongs to N
Every element is it inverse.
It a group code.
 Example 3: Consider the following (3, 8) encoding function e: B3 B8 defined by
Example 3: Consider the following (3, 8) encoding function e: B3 B8 defined by
 e (000) =00000000
e (000) =00000000
e (001) =10110000
e (010) =00101101
 e (011) =10010101
e (011) =10010101
e (100) =10100100
e (101) =10001001
e (110) =00011100
e (111) =00110001
How many errors can e detect?
Sol: There will be 8C2 = 28 pairs of code words. The minimum distance is 3. By the above theorem if minimum distance is k + 1 = 3, then the coding function can detect 2 = k or less errors.
Example 4: Show that (3, 7) encoding function e defined below is a group code.
e (000) =0000000 e (001) =0010110 e (010) =0101000
e (011) =0111110 e (100) =1000101 e (101) =1010011
e (110) =1101101 e (111) =1111011
How many errors can it detect?
Sol.:
| 0000000 | 0010110 | 0101000 | 0111110 | 1000101 | 1010011 | 1101101 | 1111011 |
0000000 | 0000000 | 0010110 | 0101000 | 0111110 | 1000101 | 1010011 | 1101101 | 1111011 |
0010110 | 0010110 | 0000000 | 0111110 | 0101000 | 1010011 | 1000101 | 1111011 | 1101101 |
0101000 | 0101000 | 0111110 | 0000000 | 0010110 | 1101101 | 1111011 | 1000101 | 1010011 |
0111110 | 0111110 | 0101000 | 0010110 | 0000000 | 1111011 | 1101101 | 1010011 | 1000101 |
1000101 | 1000101 | 1010011 | 1101101 | 1111011 | 0000000 | 0010110 | 0101000 | 0111110 |
1010011 | 1010011 | 1000111 | 1111011 | 1101101 | 0010110 | 0000000 | 0111110 | 0101000 |
1101101 | 1101101 | 1111011 | 1000101 | 1010011 | 0101000 | 0111110 | 0000000 | 0010110 |
1111011 | 1111011 | 1101101 | 1010011 | 1000101 | 0111110 | 0101000 | 0010110 | 0000000 |
From the diagonal elements of the above table, we see that (0000000) is an identity and it belongs to N.
From the table we also see that if x, y belongs to N then x y belongs to N.
Every element is its inverse.
N is a subgroup of B7 and the given encoding function is a group code.
The minimum distance is 2. Hence, the code can detect 1 or less errors.
Question bank
Prove that set A (0,1,2,3,4,5) is a finite abelian group under addition modulo 6.
Let S = (a, b, c, d) and R= (p, q, r, s) consider following operation.
* | a | b | c | d |
A | a | b | c | d |
B | b | a | a | c |
C | b | d | d | c |
d | a | b | c | d |
* | p | q | r | s |
p | p | q | r | s |
q | q | p | p | r |
r | q | s | s | r |
s | p | q | r | s |
Let f(a)= p, f(b)=q, f(c)=r, f(d)=s. Show that f is isomorphism.
Let g be set of all n zero real numbers and let a*b= ab\2. Show that (G, *) is an abelian group.
Show that (2, 5) encoding function e B2 B5 defined by
e (00) = 00000 e (10) = 10101
e (01) = 01110 e (11) = 11011
is a group code.
Find the minimum distance f (2,4) encoding function
E (00) =0000
E (10) =0110
E (01) =1011
E (11) =1100
Key takeaways
E: Bm Bn is called a group code if
E(Bm) = {e(b)/ b EBM}
= Range (e)
Let (s, *) and (S’, *) be two semi group. A function f: S S’ is called an isomorphism if s is one to one and onto and if
f(a+b) =f(a)*f(b). for all a, b in S
Procedure to find the isomorphism
 Step 1: we define the function f: S S’ with domain of f=S
Step 1: we define the function f: S S’ with domain of f=S
Step 2: We shall show that f is one to one.
Step 3: We shall show that f is onto.
Step 4: We shall show that f(a*b) = f(a)*’ f(b).
Q1. Let S be the set of all even integers. Show that the smi groups (Z, +) and (S, +) are isomorphic
 Step 1: we define the function f: Z S where f(a)=2a
Step 1: we define the function f: Z S where f(a)=2a
Step 2: suppose f(a1) =f(a2). Then 2a1=2a2. Hence f is one to one
Step 3: Suppose b is an even integer. Then a=b/2 € Z and f(a)= f(b/2) = 2(b/2) =b. hence fits onto.
Step 4: We have f (a+b) = 2(a+b) = 2a+2b= f(a)+f(b)
Hence (Z, +) and (S, +) are isomorphic.
An isomorphism from a semi group (S, *) to (S, *) itself is called an automorphism (auto=self) on (S, *)
Key takeaways
Let (s, *) and (S’, *) be two semi group. A function f: S S’ is called an isomorphism if s is one to one and onto and if
f(a+b) =f(a)*f(b). for all a, b in S
Homomorphism: In mathematics, an algebra homomorphism is a homomorphism between two associative algebras, more precisely, if A and B, are algebras over a field (or commutative ring) K, it is a function F: A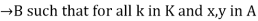
The first two conditions say that F is a module homomorphism.
If F admits an inverse homomorphism, or equivalently if it is bijective, F is said to be an isomorphism between A and B.
Normal Sub Group: A Subgroup N of a group G is called a Normal Subgroup of G if it is invariant under conjugation that is the conjugation of an element of N by an element of G is always in N. The usual notation for this relation is N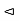 G, and the definition may be written in symbol as
G, and the definition may be written in symbol as
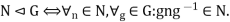
Congruence Relations: If a and b are integers and m is a positive integer, them a is congruent to b modulo m if m divides a-b.
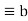
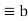
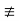
Example 1: Let 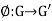 be a group homomorphism, and let H=ker (
be a group homomorphism, and let H=ker (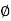 ). Let a
). Let a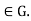 Then, the set
Then, the set 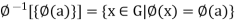 is the left coset aH of H, and is also the right coset Ha of H, Consequently, the two partitions of G into left cosets and into right cosets of H are the same.
is the left coset aH of H, and is also the right coset Ha of H, Consequently, the two partitions of G into left cosets and into right cosets of H are the same.
Proof: (a) It is a homomorphism, because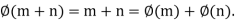
(b) It is not a homomorphism, because 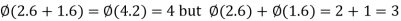 .
.
(c) It is a homomorphism, because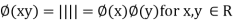 *
*
(d) It is a homomorphism, because 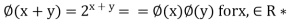
Example 2: The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.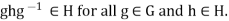
2.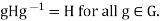
3.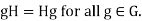
Proof: (1)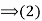 Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that 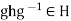 for all g
for all g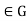 and all h
and all h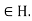 Then
Then 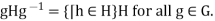
We claim that actually 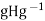 =H.We must show that H
=H.We must show that H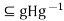 for all g
for all g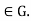
Let h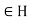 . Replacing g by
. Replacing g by 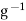 in the relation
in the relation 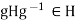 , we obtain
, we obtain 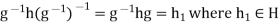 .
.
Consequently,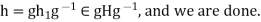
(3) Suppose that gH=Hg for all g
Suppose that gH=Hg for all g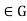 . Then
. Then 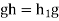 , So
, So 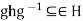 for all g
for all g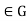
And all 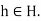 By the preceding paragraph, this means that
By the preceding paragraph, this means that 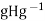 =H for all g
=H for all g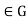 .
.
(2)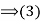 Conversely, if
Conversely, if 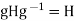 for all g
for all g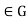 then
then 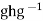 =
=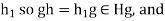 gH
gH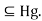 But also,
But also, 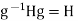 giving
giving 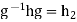 ,so that hg=g
,so that hg=g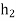 and Hg
and Hg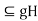 .
.
Example:3 Prove that congruence modulo n is an equivalence relation on Z.
Solution:
1) Reflexivity: For any a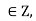 we have
we have 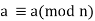 because a-a = 0 is divisible by n. hence relation is reflexive.
because a-a = 0 is divisible by n. hence relation is reflexive.
2) Symmetry: suppose a  b (mod n)
b (mod n)
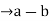 is divisible by n
is divisible by n 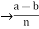 = k, for some k
= k, for some k 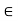 z
z  a-b = nk
a-b = nk
Therefore, b-a = -(a-b) = -nk= n(-k)
Thus, the relation is symmetric.
3) Transitivity: Suppose a  b (mod n) and b
b (mod n) and b  c (mod n), then
c (mod n), then 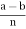 = k and
= k and 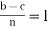
By adding these two equations we get, a-c = n(k+1) 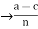 = k+l
= k+l
So, a-c is divisible by n as k+1 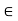 Z, i.e., a
Z, i.e., a  c (mod n)
c (mod n)
Thus, the relation is transitive.
Hence this is an equivalence relation on Z.
Ring: A Ring 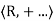 is a set R together with two binary operations + and ..., called addition and mication, defined on R such that the following axioms are satisfied
is a set R together with two binary operations + and ..., called addition and mication, defined on R such that the following axioms are satisfied
(1)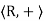 is an abelian group,
is an abelian group,
(2) Multiplication is associative,
(3) For all a, b, c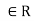 ,the left distributive law, a.(b+c) =a. b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
,the left distributive law, a.(b+c) =a. b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
Integral Domains: We know that the product of any two non-zero integers is always nonzero. But this may not be the case of arbitrary rings. For example, consider the ring 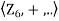 . Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in
. Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in 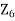 . We call these type of elements as 0 divisors.
. We call these type of elements as 0 divisors.
Field: A nonzero commutative ring in which every nonzero element has a multiplicative inverse is called a field.
Example1: The cancellation laws hold in a ring R if and only if R has no divisors of 0.
Proof: Assume that R is a ring in which the cancellation laws hold and let ab=0 for some a, b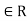 .If a
.If a by right cancellation law. Thus, R has no divisors of 0, if the cancellation laws hold in R.
by right cancellation law. Thus, R has no divisors of 0, if the cancellation laws hold in R.
Conversely, suppose that R has no divisors of 0, and suppose that ab=ac, with a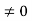 . Since a
. Since a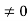 and since R has no divisors of 0, we have 0=ab-ac=a(c)
and since R has no divisors of 0, we have 0=ab-ac=a(c) 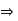 b-c =0
b-c =0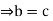 .In similar way, b a=ca with a
.In similar way, b a=ca with a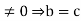 . Thus, if R has no divisors of 0, the cancellation laws hold in R.
. Thus, if R has no divisors of 0, the cancellation laws hold in R.
Example 2: Every field F is an integral domain.
Proof: Let 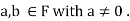 Assume that ab=0. Since
Assume that ab=0. Since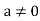 ,the multiplicative we
,the multiplicative we
Inverse 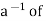 a exists, multiplying the above equation on both sides by
a exists, multiplying the above equation on both sides by 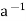 , weget
, weget
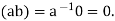 Hisimplies, 0=
Hisimplies, 0=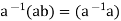 b=eb=b, which shows that F has
b=eb=b, which shows that F has
No divisors of 0. Since F is a field, in particular F is a commutative ring with unity, and we showed that F has no divisors of 0. Hence F is an integral domain.
We know that Z is an integral domain, but not a field. We next prove that finite integral domains are fields.
Example 3: Consider the map det of 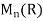 into R where det(A) is the determinant of the matrix A for A
into R where det(A) is the determinant of the matrix A for A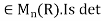 a ring homomorphism? Justify your answer.
a ring homomorphism? Justify your answer.
Solution: Because det(A+B) need not equal det(A)+det(B), we say that det is not a ring homomorphism. For example,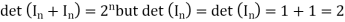
Key takeaways-
(1)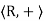 is an abelian group,
is an abelian group,
(2) Multiplication is associative,
(3) For all a, b, c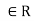 ,the left distributive law, a.(b+c) =a. b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
,the left distributive law, a.(b+c) =a. b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
Definition-
A Boolean algebra is a distributed complemented lattice having at least two members as well as 0 and 1.
A Boolean algebra is denoted by 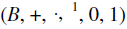 .
.
Here (B, +,.) is a lattice which has two binary operations + and., called the join and meet respectively is a unary operation in B.
The following axioms are satisfied-
2. For every for all, 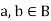
(i) 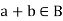
(ii) 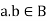
3. For all 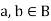 [commutative laws]
[commutative laws]
(i) 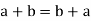
(ii) 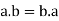
4. For all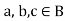 [associative law]
[associative law]
(i) 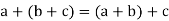
(ii) 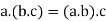
5. For all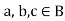 [distributive law]
[distributive law]
(iii) 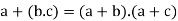
(iv) 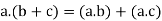
6. There exists of B such that-
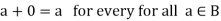
Element 0 is called the zero elements.
7. There exists 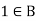 sum that-
sum that-
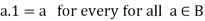
1 is called the unit element.
8. Existence of complement- for every for all 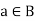 there exists an element
there exists an element 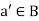 such that-
such that-
(i) a + a’ = 1 and (ii) a.a’ = 0
Note- in Boolean algebra-
0’ = 1
1’ = 0
Theorem-1- 
Proof:
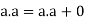
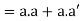
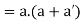
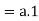
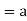
Theorem- for any 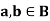
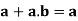
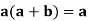
Proof:
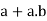
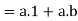
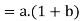
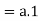
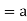
we have-
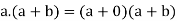
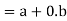
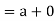
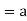
Key takeaways
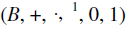
0’ = 1
1’ = 0
4. 
Lattices-
A lattice is a partially ordered set 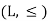 in which every pair of elements a, b
in which every pair of elements a, b 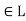 has a greatest lower bound and a least upper bound
has a greatest lower bound and a least upper bound
For example-
Suppose S be a non-empty set and L = P(S); 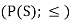 that means (
that means (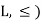 is partially ordered.
is partially ordered.
If X and Y are two elements of L, then-
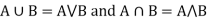
Hence (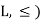 is a Lattice.
is a Lattice.
Bounded lattice-
If L is a lattice, then every pair of elements of L has a least upper bound and a greatest lower bound. If A is a finite subset of A, then A has both the least upper bound and greatest lower bound. This property may not hold if A is not a finite subset of L, we find the greatest lower bound and least upper bound of a subset of a lattice as follows.
Let (L, ⋅, +) be a lattice and A ≤L be a finite subset of L. The greatest and least upper bound of Aare defined as
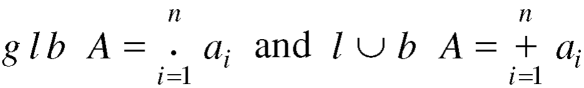
Where A = {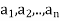 }.
}.
Note-
1. A lattice is called complete if each of its non-empty subsets has a least upper bound and a greatest lower bound.
2. Let (L, ⋅, +, 0, 1) be a bounded lattice and a ∈L. If there exists an element b ∈L
Such that
a⋅b= 0 and a + b = 1
Then b is called the complement of a
3. Let A be a non-empty set and L = P (A). Then every element of L has a complement.
Sub lattice
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Example: Let 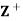 be the set of all positive integers and let D denote the relation “division” in
be the set of all positive integers and let D denote the relation “division” in 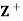 such that for any a, b ∈
such that for any a, b ∈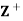 , a D b if a divide 6. Then (
, a D b if a divide 6. Then (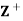 , D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
, D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
The direct product of the lattices-
Let (L1, *, +) and 2 (L, ∧, ∨) be two lattices. The algebraic system (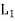 ×
× 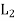 , ..., +) in which the binary operation + and ‘.’are on
, ..., +) in which the binary operation + and ‘.’are on 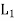 ×
× 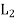 defined as
defined as
(a1, b1) ⋅ (a2, b2) = (a1 ∗a2, b1 ∧b2)
(a1, b1) + (a2, b2) = (a1 ⊕a2, b1 ∨b2) for all (a1, b1) and (a2, b2) (a2, b2) ∈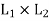 is called the direct product of the lattices
is called the direct product of the lattices 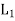 and
and 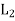
Distributive lattice-
A lattice (L, ⋅, +) is called a distributive lattice if for any a, b, c ∈L
a⋅ (b + c) = (a ⋅b) + (a ⋅c) and
a + (b ⋅c) = (a + b) ⋅ (a + c)
Note- The power set of a non-empty set A is a lattice under the operation ∩and ∪is a distributive lattice.
The dual of any expression E is obtained by interchanging the operation + and * and also interchanging the corresponding identity elements 0 and 1, in original expression E.
Truth Tables for the Laws of Boolean
Boolean | Description | Equivalent | Boolean Algebra |
A + 1 = 1 | A in parallel with |
| Annulment |
A + 0 = A | A in parallel with |
| Identity |
A. 1 = A | A in series with |
| Identity |
A. 0 = 0 | A in series with |
| Annulment |
A + A = A | A in parallel with |
| Idempotent |
A. A = A | A in series with |
| Idempotent |
NOT A = A | NOT NOT A |
| Double Negation |
A + A = 1 | A in parallel with |
| Complement |
A. A = 0 | A in series with |
| Complement |
A+B = B+A | A in parallel with B = |
| Commutative |
A.B = B. A | A in series with B = |
| Commutative |
A+B = A. B | invert and replace OR with AND |
| de Morgan’s Theorem |
A.B = A+B | invert and replace AND with OR |
| de Morgan’s Theorem |
Key takeaways
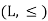
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
A Boolean algebra is a distributed complemented lattice having at least two members as well as 0 and 1.
A Boolean algebra is denoted by 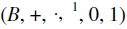 .
.
Here (B, +,.) is a lattice which has two binary operations + and., called the join and meet respectively is a unary operation in B.
The following axioms are satisfied-
There exist at least two elements a, b in B, and that ‘a’ is not equals to ‘b’.
For every for all, 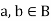
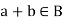
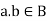
For all 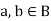 [commutative laws]
[commutative laws]
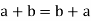
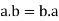
For all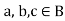 [associative law]
[associative law]
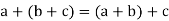
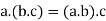
For all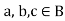 [distributive law]
[distributive law]
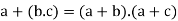
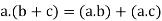
There exists of B such that-
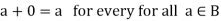
Element 0 is called the zero elements.
There exists 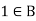 sum that-
sum that-
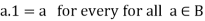
1 is called the unit element.
Existence of complement- for every for all 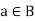 there exists an element
there exists an element 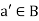 such that-
such that-
(i) a + a’ = 1 and (ii) a.a’ = 0
Note- in Boolean algebra-
0’ = 1
1’ = 0
Theorem-1- 
Proof:
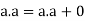
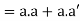
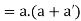
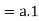
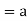
Theorem- for any 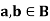
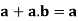
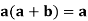
Proof:
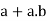
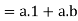
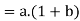
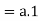
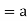
we have-
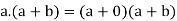
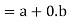
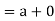
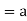
Boolean function-
Suppose (B, +,., ‘, 0, 1) be a Boolean algebra.
A function 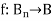 which is associated with a Boolean expression in ‘n’ variables is called a Boolean function.
which is associated with a Boolean expression in ‘n’ variables is called a Boolean function.
To transform Boolean expression E into a sums-of-products form- first, we use
De Morgan’s laws and involution law, to convert E into a form which contains only sum and products of literals then we use distributive law to transform E into a sums-of-products form. Again, to transform each product in E into 0 or a fundamental product. This is done by using the commutative, idempotent, and complement laws. Finally, we use the absorption law to get the sums-of-product form of E.
To obtain a complete sum-of-product form of E. We involve all the variables in each product of the sum of- product form of E.
Example: Express-
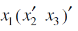
in an equivalent sum-of-products canonical form in three variables 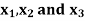
Sol.
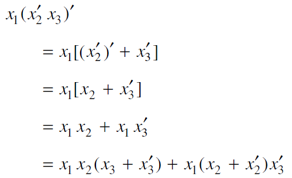
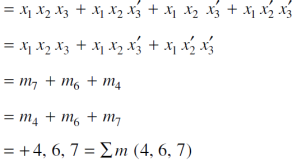
Boolean Expression
Example: Simplify z (y+z) ((x + y + z).
Sol.
z (y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Example: Simplify Y = (P + Q) (P + Q′) (P′+ Q)
Sol.
Y = (P + Q) (P + Q′) (P′+ Q)
= (P P+ P Q′+ P Q + Q Q′) (P′+ Q)
= (P + P Q′+ P Q + 0) (P′+ Q)
= (P + P Q′+ P Q) (P′+ Q)
= P P1 + P Q + P Q′P′+ P Q′Q + P Q P′+ P Q Q
= 0 + P Q + 0 + 0 + 0 + P Q
= P Q + P Q
= P Q
Example: Minimize the expression 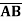 +
+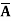 + A B
+ A B
Sol.
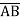 +
+ 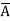 + A B
+ A B
= 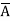 +
+ 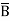 +
+ 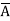 + A B
+ A B
= 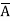 +
+ 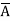 +
+ 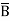 + A B
+ A B
= 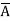 +
+ 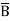 + A B
+ A B
= 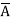 + A B +
+ A B + 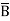
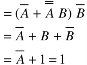
Hence
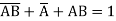
Key takeaways
A function  which is associated with a Boolean expression in ‘n’ variables is called a Boolean function
which is associated with a Boolean expression in ‘n’ variables is called a Boolean function
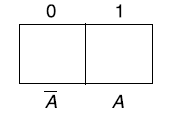
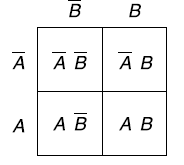
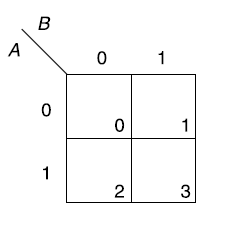
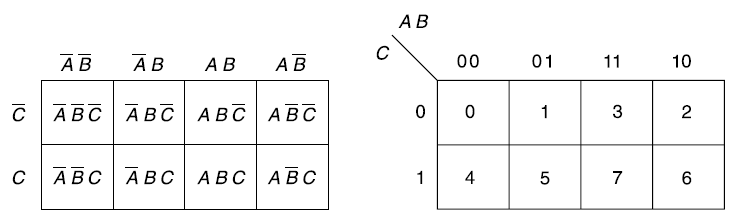
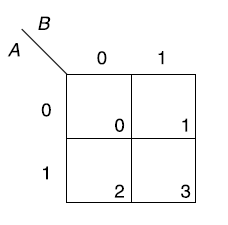
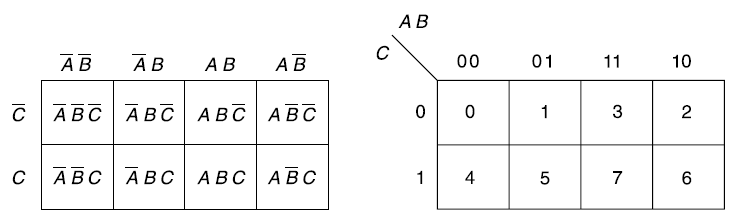
The Karnaugh method is a systematic method for simplifying Boolean function.
It is a graphical representation of the truth table with a square representing each min term.
If a function has ‘n’ variables then the Karnaugh map will have 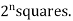
One variable Karnaugh map is-
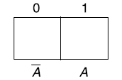
Two variable Kanaugh map representing min term-
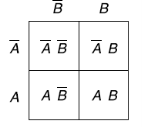
Or
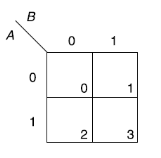
Karnaugh map for three variables-
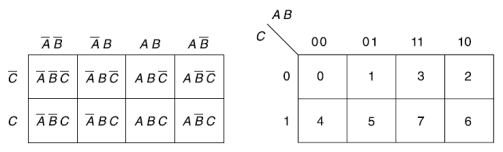
The Boolean algebra is the system of mathematical logics. Here we will discuss the logic gates which are electronic circuits that can be used to actually implement the most elementary logical expressions, called as logic gates.
The three basic gates are-
Other logic gates that are derived from these three basic gates are NAND-gate, the NOR gate, the EX-OR- gate and the EX-NOR gate.
Here we will start form OR-gate-
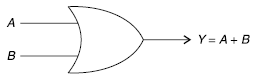
OR-gate-
This is a logic circuit with two or more than two inputs and outputs.
The output is 0 only when all of its inputs are at logic 0.
We symbolize OR-gate with the following symbol-
And the truth table is given as-
P | Q | Y |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
The operation of an OR-gate which is explained by the expression Y = A + B is read as Y equal to A OR B.
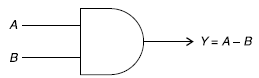
AND-gate
An AND-gate is a logic circuit having two or more than two inputs and one output. The output of an
AND-gate is logic ‘1’, only when all of its inputs are in ‘1’ state. In all other possible combination, the output is ‘0’.
We symbolize AND-gate with the following symbol-
And the truth table is given as-
A | B | Y |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
The operation of an AND-gate is given by:
Y = A + B
NOT-gate
NOT-gate is one input and one output logic gate. The output of a NOT-gate is always the complement of the input. It is also known as an inverter or a complementing circuit
We symbolize NOT-gate with the following symbol-
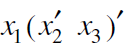
And the truth table is given as-
A |
|
0 | 1 |
1 | 0 |
NOR-gate
It has two or more input, but produces only are output.
We symbolize NOR-gate with the following symbol-
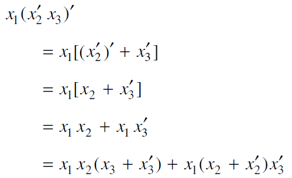
And the truth table is given as-
A | B | Z |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
NAND- gate
NAND-gate function is a composite function. In this case an AND function is complemented to produce a NAND function placing an N in front of AND. The NAND-gate has two or more input signals but only one output signal. The NAND-gate is a contraction of NOT AND. It can have many inputs.
We symbolize NOR-gate with the following symbol-
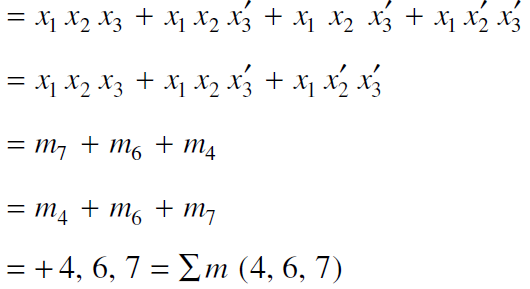
And the truth table is given as-
A | B | Z |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
EX-OR gate
It differs from an OR gate in only is of the entries in the truth table.
The EX-OR gate can also L are having two or more inputs but produces one output signal.
We symbolize NOR-gate with the following symbol-
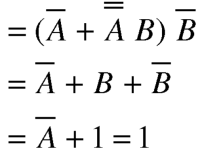
And the truth table is given as-
A | B | Z |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
EX-NOR gate
The EX-NOR gate is logically equivalent to an inverted EX-OR gate.
We symbolize NOR-gate with the following symbol-
And the truth table is given as-
A | B | Z |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
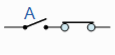
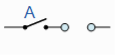
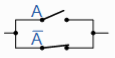
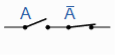
Example: What will be logic circuit of the input-output Boolean expression-
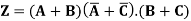
Sol.
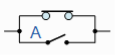
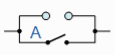
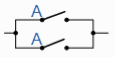
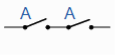
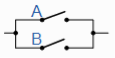
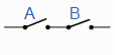
Example: Show that the following logic circuits are equivalent.
And
Sol.
Here we will use logic tables in order to prove the above logic gates are equivalent.
Hence the tables will be-
Logic table for first circuit
A | B | Y |
1 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
And
Logic table for second circuit
A | B | Y |
1 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
Hence the circuits are equivalent.
Key takeaways
This is a logic circuit with two or more than two inputs and outputs.
The output is 0 only when all of its inputs are at logic 0.
2. AND-gate
An AND-gate is a logic circuit having two or more than two inputs and one output. The output of an
AND-gate is logic ‘1’, only when all of its inputs are in ‘1’ state. In all other possible combination, the output is ‘0’.
3. NOT-gate
NOT-gate is one input and one output logic gate. The output of a NOT-gate is always the complement of the input. It is also known as an inverter or a complementing circuit
References: