Unit - 5
Graphs and Trees
Basic Terminology:
Graph:
A graph (V, E) is an ordered pair, whose V is finite non-empty set elements are called vertices and ‘E’ is a set of un-ordered pair of distinct vertices of ‘V’.
i.e. (V, E) – where V is Finite non-empty set
where is E is unordered pairs (edges)
Example 1: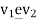 
2: V =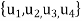 
, E =
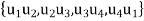
Note 1: Vertices is also known as points, nodes and functions
2: Edge is also as line, are branch and link
3. If the edge e =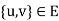
then u and v are both said to be incident with ‘e’ and adjacent to each other u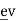
4.If e=u, v and e’=v, w are edges is G, then we say that edges e and e’ are adjacent edges
Simple graph:
Multi Graph:
A multi graph G= (V, E) is an ordered pair of sets, where ‘V’ is finite and non-empty set and ‘E’ is set of un-ordered pairs of distinct elements of v and repetitions are allowed in the classes.
Pseudo Graph:
A Pseudo graph G= (V, E) is ordered pairs, where ‘v’ is finite and non-empty E is set of un-ordered pairs of distinct elements of V and repetitions are allowed in the classes.
Note: Multi-graph and Pseudo-graph same but self-loop in the pseudo.
Dia –Graph:
A dia-graph G= (V, E) is an ordered pair, where ‘v’ is non-empty finite set and E is the set of unordered pairs of distinct vertices of V.
Weight –Graph:
A graph or dia-graph G= (V, E) is said to be weighted graph if there-exist a functions w: E
which assign a real number to each edge.
Note: If u=u. v is an edge in a weighted graph then its weight is denoted by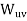 
.
Source: Let G= (V, E) be a dia-graph. A vertex which has no arcs directed towards it is called source.
Sink:
A vertex which has no arcs directed away from it. Then it is called sink.
Network:
A network is a dia-graph which possess exactly one source and one sink, the vertices of a network are called nodes.
Label –Graph:
A graph is which all the vertices are distinct variables one from other (or) another is called Label graph
Isomorphic Graph:
Let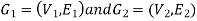 
be two graphs then 
,
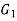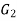are said to be isomorphic if they have same number of vertices and same number of edges.
Non-Isomorphic Graphs:
Connected –Graphs: A graph is said to be connected-graph if every pair vertices in G are joined by a path.
Dis-Connected Graph:
A graph which is not connected is called dis-connected graph.
A Cyclic-Graph:
A Graph without cycles is called as A-cyclic graph.
Sub Graph:
A Graph is said to be Sub-graph of G if all the vertices and all the edges of g are on G, and each edge of g has same and vertices in g as in G.
Null-graph:
A graph G= (V, E) is said to be a null-graph if it has no edges.
Complete graph:
A Graph G= (V, E) is said to be complete graph if every pair of vertices are directly connected by single edge.
Bipartite Graphs-
A graph G (V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subsets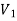 
and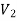 
such that each edge is G had end vertex is 
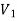and other end vertex in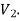 
There is no edge between two vertices of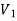 
as well as there is no edge between two vertices of 
.
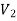Here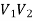 
bipartition of V.
Regular Graphs-
If all vertices of a graph G have same degree, then G is called as a regular graph.
Note- In any graph the number of vertices with odd degree must be even.
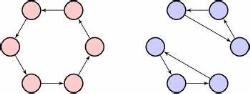
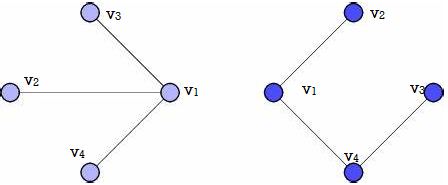
Example: Consider the graphs given below-
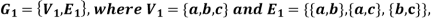
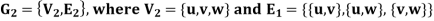
Check whether these graphs are same or not?
Sol.
As we can see that these graphs are not same because here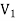 
and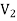 
are not same since 
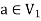but a does not belongs to 
.
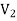These two graphs look same but not equal.
We can draw these graphs as below-
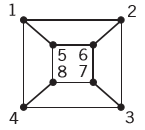
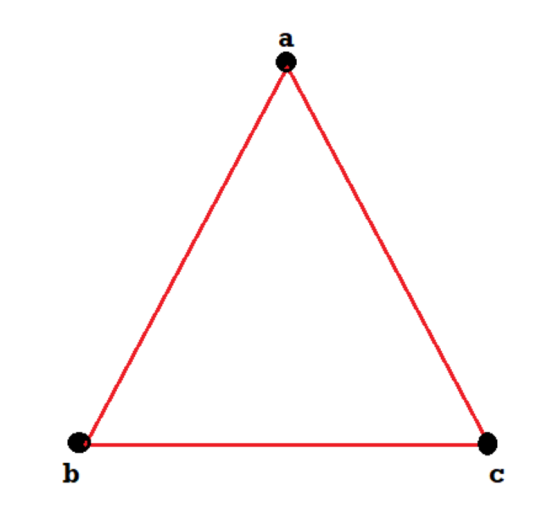
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.
Key takeaways
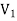
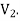
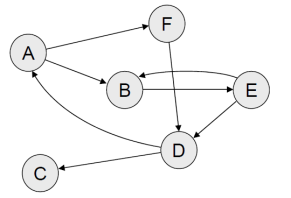
Digraphs are the directed graph.
Definition-
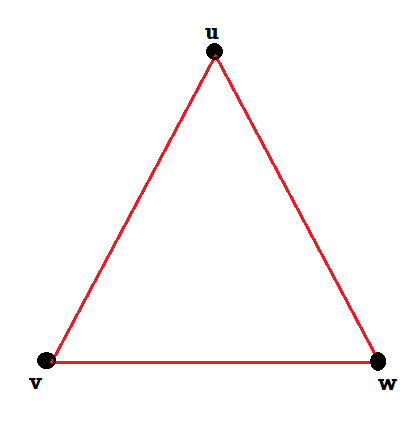
Let G = (V, E) be a graph. If the elements of E are ordered pairs of vertices, then the graph G is called a directed graph.
The vertex u is called the origin or initial point of the directed edge e and v is called the destination or terminal point of e.
The example of the digraph is-
Note-
Graph representation of relation-
A relation can be represented by drawing graph. Suppose R is a relation on the set A = {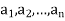
}.
Then elements of are represented by points called nodes.
If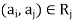 
then we connect the vertices 
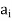and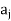 
by means of an arc and put an arrow in the direction from 
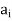to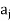 
.
If (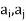
) ∈R and (
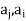) ∈R then we draw two arcs between 
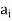and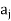 
(sometimes by one arc which starts from node ai and relatives to node xi (such an arc is called a loop). When all the nodes corresponding to the ordered pairs in R are connected by arcs with proper arrows, we get a graph of the relation R. If Ris reflexive, then there must be a loop at each node in the graph of R. If R is symmetric, then (
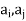) ∈R implies (
, 
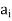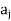) ∈R and the nodes ai and aj will be connected by two arcs (edges) one from ait o aj and the other from aj to ai.
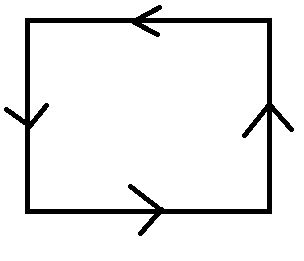
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4), (4, 1), (4, 4)}
Represent the relation by graph.
Sol.
The diagraph of R can be made as-
Key takeaways
A directed graph (V, E) is said to be finite if its set V of vertices and its set E of edges are finite
3. If the edges and/or vertices of a directed graph G are labeled with some type of data, then G is called a labeled directed graph.
Graph isomorphism:
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H
f: V(G)
V(H)
such that any two vertices u and v of G are adjacent in G iff f(u) and f(v) are adjacent in H. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection
If an isomorphism exists between two graphs, then the graphs are called isomorphic and denoted as G
. In the case when the bijection is a mapping of a graph onto itself, i.e., when G and H are one and the same graph, the bijection is called an auto morphism of G.
Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to each other is called an isomorphism class of graphs.
The two graphs shown below are isomorphic, despite their different looking drawings.
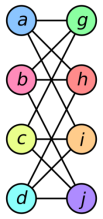
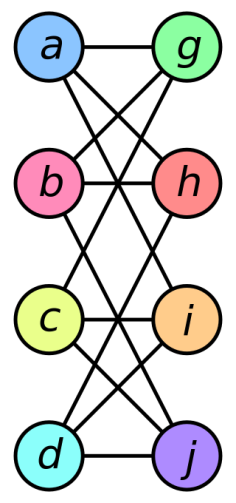
EXAMPLE 1:
SOLUTION: The isomorphism for the above is,
f(a)=1, f(b)=6, f(c)=8, f(d)=3, f(g)=5, f(h)=2, f(i)=4, f(j)=7.
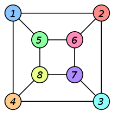
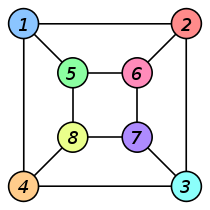
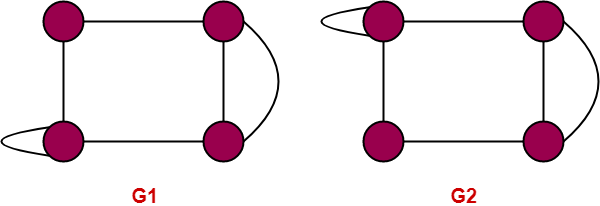
Example 2: Are the two following graphs are isomorphic?
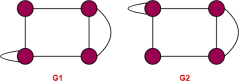
Solution:
We check the necessary and sufficient conditions for the given graphs to be isomorphic
Condition 1: number of vertices in G1 =4
Number of vertices in G2= 4
Here both G1 and G2 have same number of vertices hence the condition satisfied.
Condition 2: number of edges in G1 = 5
Number of edges in G2 = 6
Here they are not equal, therefore the condition is not satisfied.
Hence the given graphs are not isomorphic.
Connectivity:
A graph is a connected graph if, for each pair of vertices, there exists at least one single path which joins them. A connected graph may demand a minimum number of edges or vertices which are required to be removed to separate the other vertices from one another. The graph connectivity is the measure of the robustness of the graph as a network.
In a connected graph, if any of the vertices are removed, the graph gets disconnected. Then the graph is called a vertex-connected graph. On the other hand, when an edge is removed, the graph becomes disconnected. It is known as an edge-connected graph.
There are different types of connected graphs explained in Maths. They are:
Let us learn them one by one.
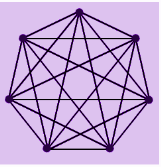
Example.1: If a complete graph has a total of 20 vertices, then find the number of edges it may contain.
Solution: The formula for the total number of edges in a k15 graph is given by;
Number of edges =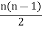 
=
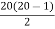
=10(19)
=190
Hence, it contains 190 edges.
Example.2: If a graph has 40 edges, then how many vertices does it have?
Solution: As we know,
Number of edges = =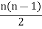 
40 =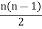 
n(n-1) = 80
n2 – n – 80 = 0
On solving the above quadratic equation, we get;
n ≈ 9.45, -8.45
Since, the number of vertices cannot be negative.
Therefore, n ≈ 9
Following are basic operations of a Graph −
Add Vertex − Adds a vertex to the graph.
Add Edge − Adds an edge between the two vertices of the graph.
Display Vertex − Displays a vertex of the graph.
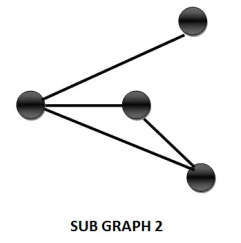
Sub graph
Getting a sub graph out of a graph is an interesting operation. A sub graph of a graph G (V, E) can be obtained by the following means:
1. Removing one or more vertices from the vertex set.
2. Removing one or more edges from the edge family.
3. Removing either vertices or edges from the graph.
4. The vertices of sub graphs are subsets of the original vertices
5. The edges of sub graphs are subsets of the original edges
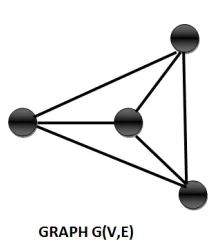
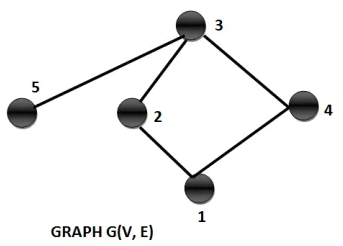
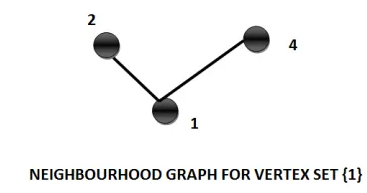
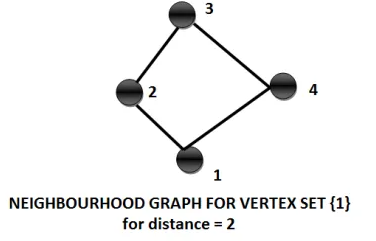
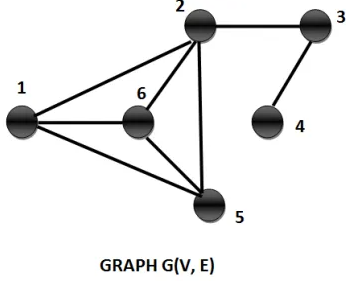
Neighbourhood graph
The neighbourhood graph of a graph G (V, E) only makes sense when we mention it with respect to a given vertex set. For e.g., if V = {1,2,3,4,5} then we can find out the Neighbourhood graph of G (V, E) for vertex set {1}.
So, the neighbourhood graphs contain the vertices 1 and all the edges incident on them and vertices connected to these edges.
Example:
Example:
Spanning Tree
A spanning tree of a connected graph G (V, E) is a sub graph that is also a tree and connects all vertices in V. For a disconnected graph the spanning tree would be the spanning tree of each component respectively.
There is an interesting set of problems related to finding the minimum spanning tree (which we will be discussing in upcoming posts). There are many algorithms available to solve this problem, for e.g.: Kruskal’s, Prim’s etc. Note that the concept of minimum spanning tree mostly makes sense in case of weighted graphs. If the graph is not weighted, we consider all the weights to be one and any spanning tree becomes the minimum spanning tree.
We can use traversals like Breadth First Scan and Depth First Scan to fight the Spanning Tree. We can find spanning tree for undirected graphs, directed graphs, multi graphs as well.
Example:
Conversion from Directed Graph to Undirected graph
This is the simplest conversions possible. A directed graph has directions represented by arrows, in this conversion we just remove all the arrows and do not store the direction information.
Example:
Conversion from Undirected Graph to Directed graph
This conversion gives a directed graph given an undirected graph G (V, E). It is the exact reverse of the above. The trick to achieve this is to add one edge for each existing edge in the edge family E. Once the extra edges are added, we just assign opposite direction to each pair of edges between connecting vertices.
Example:
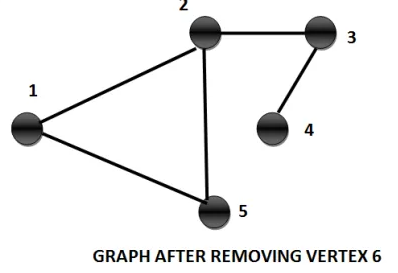
Delete Vertex
What happens when we delete a vertex from a given Graph G (V, E)?
We cannot successfully remove a vertex if we do not remove all the edges incident on the vertex. Once we remove the vertex then the adjacency matrix will not contain the row and column for the corresponding vertex.
This operation changes the vertex set and the edge family of the graph.
Example:
Key takeaways
Path-
A path is a walk that does not repeat any vertices (or edges) except perhaps the first and last. If a path starts and ends at the same vertex, it is called a cycle.
Circuit-
A Hamiltonian circuit is a closed walk in a graph which visits each vertex exactly once. The start and end vertex (which happens to be the same) is visited twice.
In a Hamiltonian Circuit of N vertices, there would be exactly N edges. Since a Hamiltonian Circuit cannot visit the same vertex twice, hence there cannot be any loops or parallel edges. Thus, all such circuits are simple graphs. And to connect each of the N vertex we need N-1 edges, to connect the first and the last vertex and close the walk, we need one more edge. Hence, N vertex Hamiltonian circuit will have exactly N edges.
If you remember from our last post, we proved that the necessary and sufficient condition for Euler Lines is that each vertex must have even degree. On the same lines if we try to establish a necessary and sufficient condition for existence of Hamiltonian Circuit in a graph we will miserably fail.
Key takeaways
A multigraph is said to be traversable if it “can be drawn without any breaks in the curve and without repeating any edges,” that is, if there is a path which includes all vertices and uses each edge exactly once.
Or in other words-
A graph G is said to be traversable, if it has a path.
If G is connected graph and u and v are any two vertices of G, the length of the shortest path between u and v is called the distance between u and v and is denoted by d (u, v).
The distance function on defined above has the following properties. If u, v and w are any three vertices of a connected graph then.
(i) d (u, v) ≥ and d (u, v) = 0 if and only if u = v
(ii) d (u, v) = d (v, u)
(iii) d (u, v) ≤ d (u, w) + d (w, v)
The radius of a connected graph G is defined as the maximum eccentricity among all vertices of the graph. It is denoted by r.
Thus r = radius of G = min {e(v): v 
V}
Euler’s Path
An Euler’s path contains each edge of ‘G’ exactly once and each vertex of ‘G’ atleast once A conncected graph G is said to be traversible if it contains an Euler’s path.
Example
Euler’s Path=d-c-a-b-d-e.
Euler’s Circuit
In a Euler’s path, if the starting vertex is same as its ending vertex, then it is called an Euler’s circuit.
Example
Euler’s Circuit Theorem
A connected graph ‘G’ is traversable if and only if the number of vertices with odd degree in G is exactly 2 or 0. A connected graph G can contain an Euler’s path, but not an Euler’s circuit if it has exactly two vertices with an odd degree.
Note: This Euler path begins with a vertex odd degree and ends with other vertex of odd degree.
Euler’s path – b-e-a-b-d-c-a is not an Euler’s circuit, but it is an Euler’s path. Clearly it has exactly 2 odd degree vertices.
Note: In a connected graph G, if the number of vertices with odd degree=0, then Euler’s circuit exists.
Key takeaways
Hamiltonian Graph
A connected graph G is said to be Hamiltonian graph, if there exists a cycle which contains all the vertices of G.
Every cycle is a circuit but a circuit may contain multiple cycles. Such a cycle is called a Hamiltonian cycle of G.
Hamiltonian graph- A closed path that visits every vertex in G exactly once and if G admit a Hamiltonian circuit, then G is called Hamiltonian graph.
Note- A Eulerian circuit traverses every edge exactly once, but many repeats’ vertices.
While a Hamiltonian circuit visits each vertex exactly once but many repeats’ edges.
Following are the examples of Hamiltonian and Eulerian graph respectively-
Note:
Example:
Take a look at the following graph-
For the graph shown above-
G has four vertices with odd degree, hence it is not traversable. By skipping the internal edges, the graph has a Hamiltonian cycle passing through all the vertices.
The “Traveling-salesman” problem refer to finding a Hamiltonian circuit for G of minimum weight.
Theorem-The complete graph Kn with n ≥ 3 vertices has H = (n −1)! /2 Hamiltonian circuits (where we do not distinguish between a circuit and its reverse).
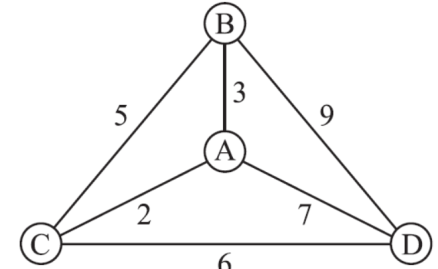
Consider the complete weighted graph G in Fig. 8-35(a). It has four vertices, A, B, C, D. By Theorem 8.13 it has H = 3! /2 = 3 Hamiltonian circuits. Assuming the circuits begin at the vertex A, the following are the three circuits and their weights:
|ABCDA| = 3 + 5 + 6 + 7 = 21
|ACDBA| = 2 + 6 + 9 + 3 = 20
|ACBDA| = 2 + 5 + 9 + 7 = 23
Thus, ACDBA with weight 20 is the Hamiltonian circuit of minimum weight.
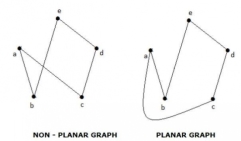
A graph 'G' is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Euler’s formula for planar graph-
For any planar graph with v vertices, e edges and f faces, we have-
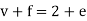
Example
Regions
Every planar graph divides the plane into connected areas called regions.
Example 1:
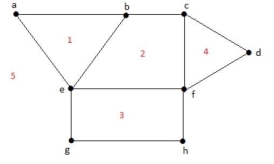
Solution: Degree of a bounded region r = deg(r) = Number of edges enclosing the regions r.
deg (1) =3
deg (2) =4
deg (3) =4
deg (4) =3
deg (5) =8
example 2:
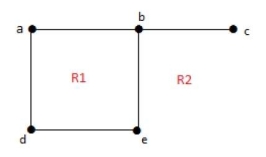
Solution: Degree of an unbounded region r = deg(r) = Number of edges enclosing the regions r.
deg (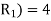
deg (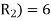
In planar graphs, the following properties hold good −
n ∑ i=1 deg (Vi) = 2|E|
n ∑ i=1 deg(ri) = 2|E|
Based on the above theorem, you can draw the following conclusions −
In a planar graph,
K|R| = 2|E|
K|R| ≤ 2|E|
K|R| ≥ 2|E|
Note− Assume that all the regions have same degree.
3. According to Euler's Formulae on planar graphs,
|V| + |R| = |E| + 2
|V| + |R|=|E| + (K+1)
Where, |V| is the number of vertices, |E| is the number of edges, and |R| is the number of regions.
4. Edge Vertex Inequality
If 'G' is a connected planar graph with degree of each region at least 'K' then,
|E| ≤ 
- 2{|v|-2}
You know, |V| + |R| = |E| + 2
K.|R| ≤ 2|E|
K (|E| - |V| + 2) ≤ 2|E|
(K - 2) |E| ≤ K (|V| - 2)
|E| ≤ 
- 2{|V| - 2}
5. If 'G' is a simple connected planar graph, then
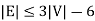
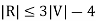
There exists at least one vertex V∈ G, such that deg(V) ≤ 5
6. If 'G' is a simple connected planar graph (with at least 2 edges) and no triangles, then
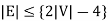
Key takeaways
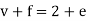
2. A graph 'G' is said to be planar if it can be drawn on a plane or a sphere so that no two edges cross each other at a non-vertex point.
Graph colouring problem is to assign colours to certain elements of a graph subject to certain constraints.
Vertex colouring is the most common graph colouring problem. The problem is, given m colours, find a way of colouring the vertices of a graph such that no two adjacent vertices are coloured using same colour.
The other graph colouring problems like Edge Colouring (No vertex is incident to two edges of same colour) and Face Colouring (Geographical Map Colouring) can be transformed into vertex colouring.
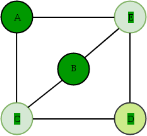
Chromatic Number:
The smallest number of colours needed to colour a graph G is called its chromatic number. For example, the following can be coloured minimum 3 colours.
Trees-
A graph T is called a tree if T is connected and T has no cycles.
A graph without cycle is said to be a cycle-free.
The tree consisting of a single vertex with no edges is called the degenerated tree.
One thing to keep in mind is that while the trees we study in graph theory are related to trees you might see in other subjects, the correspondence is not exact. For instance, in anthropology, you might study family trees, like the one below
So far so good, but while your grandparents are (probably) not blood relatives, if we go back far enough, it is likely that they did have some common ancestor. If you trace the tree back from you to that common ancestor, then down through your other grandparent, you would have a cycle, and thus the graph would not be a tree.
You might also have seen something called a decision tree (such as the algorithm for deciding whether a series converges or diverges). Sometimes these too contain cycles, as the decision for one node might lead you back to a previous step.
Both the examples of trees above also have another feature worth mentioning: there is a clear order to the vertices in the tree. In general, there is no reason for a tree to have this added structure, although we can impose such a structure by considering rooted trees, where we simply designate one vertex as the root.
Graph G is called a tree if G is connected and contains no cycles.
Graph whose connected components are trees: forest
A tree is a connected undirected graph with no simple circuits.
A (not-necessarily-connected) undirected graph without simple circuits is called a forest.
Key takeaways
A rooted tree is a tree in which one vertex has been designated as the root and every edge is directed away from the root.
Suppose that T is a rooted tree. If v is a vertex in T other than the root, the parent of v is the unique vertex u such that there is a directed edge from u to v.
If u is the parent of v, then v is called a child of u.
Vertices with the same parent are called siblings.
The ancestors of a vertex other than the root are the vertices in the path from the root to this vertex, excluding the vertex itself and including the root.
The descendants of a vertex v are those vertices that have v as an ancestor.
A vertex of a tree is called a leaf if it has no children.
Vertices that have children are called internal vertices.
If a is a vertex in a tree, the sub tree with a as its root is the sub graph of the tree consisting of a and its descendants and all edges incident to these descendants.
A rooted tree is called an m-ary tree if every internal vertex has no more than m children. The tree is called a full m-ary tree if every internal vertex has exactly m children.
Example- consider the tree below-
If we designate vertex f as the root, then e, h, and i are the children of f, and are siblings of each other. Among the other things we can say are that a is a child of c, and a descendant of f. The vertex g is a descendant of f, in fact, is a grandchild of f. Vertices g and d are siblings, since they have the common parent e.
Notice how these changes if we pick a different vertex for the root. If a is the root, then its lone child is c, which also has only one child, namely e. We would then have f the child of e (instead of the other way around), and f is the descendant of a, instead of the ancestor. fand g are now siblings.
Example: Explain why every tree is a bipartite graph.
Solution.
To show that a graph is bipartite, we must divide the vertices into two sets A and B so that no two vertices in the same set are adjacent. Here is an algorithm that does just this.
Designate any vertex as the root. Put this vertex in set A. Now put all of the children of the root in set B. None of these children are adjacent (they are siblings), so we are good so far. Now put into A every child of every vertex in B (i.e., every grandchild of the root). Keep going until all vertices have been assigned one of the sets, alternating between A and B every “generation.” That is, a vertex is in set B if and only if it is the child of a vertex in set A.
Spanning trees-
Given a connected graph G, a spanning tree of G is a sub-graph of G which is a tree and includes all the vertices of G.
Every connected graph has a spanning tree.
Example: Find two different spanning trees of the graph.
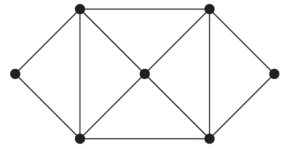
Sol-
Two spanning trees are-
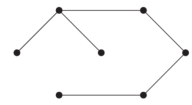
And
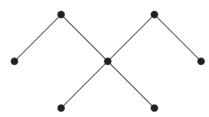
Binary Tree
An m-ary tree with m = 2 is called a binary tree.
Ordered Root Tree
An ordered rooted tree is a rooted tree where the children of each internal vertex are ordered.
Left and Right Child
In an ordered binary tree, the first child is called the left child and the second child is called the
Right child.
Left and Right Sub tree
The tree rooted at the left child is called the left sub tree and the tree rooted at the right child is
Called the right sub tree.
Example 1: Every binary tree has an odd no. Of vertices.
Solution: let T = (V, E) be a binary tree.
A part from the root every vertex in a binary tree is an odd degree.
w.k.t., there must be an even no. of vertices such odd degree.
When the root which of odd degree is added to this even no. Of vertices i.e.,
Even no. of vertices and one root vertex, we have odd no. Of vertices.
Therefore, every binary tree has odd no. of vertices
Note: let a tree has ‘n’ vertices and ‘m’ pendent vertices, then the no. of internal vertices of degree 3 is n-(m+1)
Example 2: prove that there are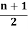 
pendent vertices in any binary tree with ‘n’ vertices.
Solution: suppose T = (V, E) be a binary tree with ‘n’ vertices. Let ‘m’ be the two no. of pendent vertices in T. Then T has (n-(m+1)) no. of internal vertices of degree 3
So, the sum of degree of all vertices in T is 3(n-m-1) + m+2…. (1)
Since T is tree with ’n’ vertices then it has (n-1) edges.
So, the degree sum of ‘n’ vertices in T is given by
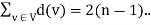(2)
From (1) and (2)
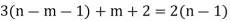
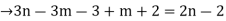
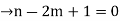
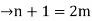
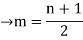
The no. of pendent vertices in binary tree is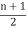 
Let G be a simple graph A spanning tree of G is a sub graph of G that is a tree containing every vertex of G.
Find the Spanning Tree.
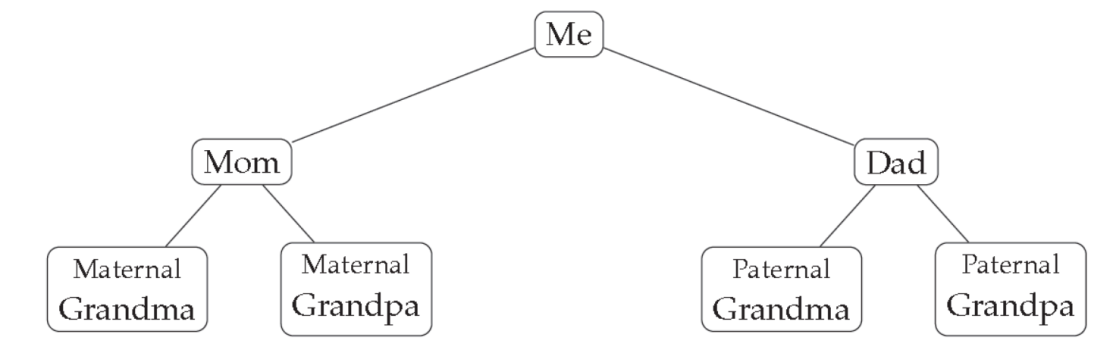
It is not a tree, because it contains simple circuit.
This subgraph is spanning tree, because it is a tree that contain vertex of G.
Minimum spanning tree
A minimum spanning tree is a connected weighted graph is a spanning tree that has the smallest possible sum of it edges.
Definition-
Let G be a connected weighted graph. A minimal spanning tree of G is a spanning tree of G whose total weight is as small as possible.
Algorithm to generate minimum spanning tree-
A connected weighted graph with n vertices.
Step 1- Arrange the edges of G in the order of decreasing weights.
Step 2- Proceed sequentially, and delete each edge of G, that does not disconnect the graph G until n – 1 edge remain.
Step 3: Exit.
KRUSKAL’S ALGORITHM:
An algorithm that is used for finding the minimum spanning tree of a connected weighted graph is known as Kruskal’s algorithm. A tree among the graph is identified which includes every vertex and where the total weight of all the edges in the tree is less than or equal to the spanning tree.
Algorithm
Step 1– All the edges of the given graph G (V, E) are arranged in the non-decreasing order in accordance with the weight of the edge.
Step 2 – The smallest weighted edge from the graph is chosen and is checked if it forms a spanning tree earlier.
Step 3 – This edge is included to the spanning tree if there is no cycle, or else it is discarded.
Step 4− Repeat Step 2 and Step 3 until (V−1) number of edges are left in the spanning tree.
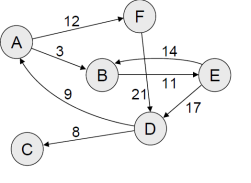
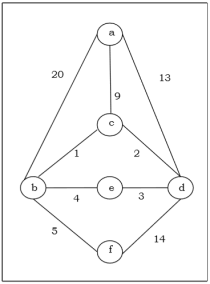
Example 1: For instance, identify the minimum spanning tree from the following graph G by using the Kruskal’s algorithm.
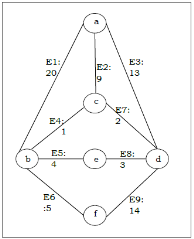
Solution
The following table is constructed from the above graph:
Edge No. | Vertex Pair | Edge Weight |
E1 | (a, b) | 20 |
E2 | (a, c) | 9 |
E3 | (a, d) | 13 |
E4 | (b, c) | 1 |
E5 | (b, e) | 4 |
E6 | (b, f) | 5 |
E7 | (c, d) | 2 |
E8 | (d, e) | 3 |
E9 | (d, f) | 14 |
In accordance with the weight of the Edge, the table is rearranged in ascending order.
Edge No. | Vertex Pair | Edge Weight |
E4 | (b, c) | 1 |
E7 | (c, d) | 2 |
E8 | (d, e) | 3 |
E5 | (b, e) | 4 |
E6 | (b, f) | 5 |
E2 | (a, c) | 9 |
E3 | (a, d) | 13 |
E9 | (d, f) | 14 |
E1 | (a, b) | 20 |
We get the required minimal spanning tree
Step-1:
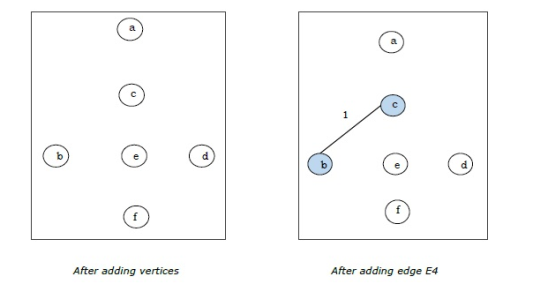
Step-2:
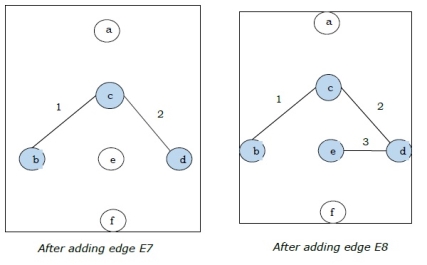
Step-3:
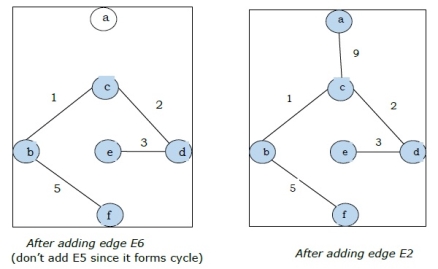
As all the edges are covered in the last figure, the algorithm is stopped and this is considered as the minimal spanning tree and the total weight of the spanning tree is (1+2+3+5+9) =20.
The minimum spanning tree for a connected weighted graph by Prim’s algorithm, developed by the mathematicians VojtechJarnik and Robert C. Prim. In the Graph, the tree that includes every vertex and total weight of all the edges in the tree is less than or equal to every possible spanning tree. Prim’s algorithm works faster on dense graphs.
Algorithm:
Example 2: For instance, consider the following graph G and identify the minimum spanning tree using Prim’s algorithm
Solution:
It is started with vertex ‘a’.
Step-1:
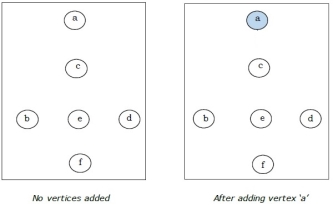
Step-2:
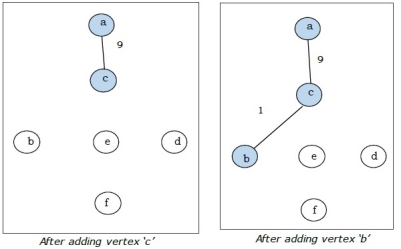
Step-3:
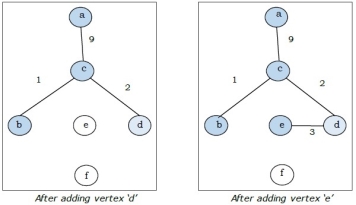
Step-4:
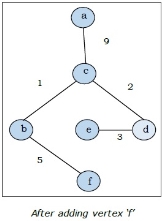
The above graph is the minimum spanning tree and the total weight is
(1+2+3+5+9) =20
References:
