Unit - 1

Introduction

1.1 Alphabet

Definition − An alphabet is any finite set of symbols.

Example − ∑ = {a, b, c, d} is an alphabet set where ‘a’, ‘b’, ‘c’, and ‘d’ are symbols.

1.2 String

●      Definition − A string is a finite sequence of symbols taken from ∑.

●      Example − ‘cabcad’ is a valid string on the alphabet set ∑ = {a, b, c, d}

1.3 Languages

●      Definition − A language is a subset of ∑* for some alphabet ∑. It can be finite or infinite.

●      Example − If the language takes all possible strings of length 2 over ∑ = {a, b}, then

L1 = {ab, aa, ba, bb} finite language

L2 = {a, aa, aaa, abb, abab} infinite language

1.4 Automata

●      It is the analysis of abstract machines and the problems of computation that can be solved by these machines.

●      The automaton is called the abstract machine.

●      The primary reason behind the development of the automata theory was the development of methods to explain and analyze the complex behaviour of separate systems.

1.5 Grammar

Simplifying Context Free Grammars

A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:

●        A non-terminal generating a terminal (e.g.; X->x)

●        A non-terminal generating two non-terminals (e.g.; X->YZ)

●        Start symbol generating ε. (e.g.; S->ε)

Consider the following grammars,

G1 = {S->a, S->AZ, A->a, Z->z}

G2 = {S->a, S->aZ, Z->a}

The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Note –

●        CNF is a pre-processing step used in various algorithms.

●        For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.

How to convert CFG to CNF?

Step 1. Remove start from RHS. If start symbol S is at the RHS of any production in the grammar, create a new production as: S0->S where S0 is the new start symbol.

Step 2. Remove null, unit and useless productions. If CFG comprises of any production rules, remove them.

Step 3. Remove terminals from RHS. For e.g.; production rule X->xY can be decomposed as: X->ZY Z->x

Step 4. Remove RHS with more than two non-terminals. e.g., production rule X->XYZ can be decomposed as:

X->PZ
P->XY

1.6 Deterministic finite automation (DFA): Formal Definition

In this, for each input symbol, the state to which the machine will move can be determined. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.

An automaton can be represented by a 5-tuple (Q, ∑, δ, q 0, F), where −

❖      Q is a finite set of states.

❖      ∑ is a finite set of symbols, called the alphabet of the automaton.

❖      δ is the transition function.

❖      q0 is the initial state from where any input is processed (q 0 ∈ Q).

❖      F is a set of final state/states of Q (F ⊆ Q).

Transition function can be defined as:

δ: Q x ∑→Q 

Representation

A DFA can be represented by digraphs called state diagram. In which:

1. The state is represented by vertices.
2. The arc labeled with an input character shows the transitions.
3. The initial state is marked with an arrow.
4. The final state is denoted by a double circle.

Advantages and disadvantages

❖      DFAs are used to model a Turing machine.

❖      They are used as++ models of computation.

❖      The union/intersection of the languages recognized by two given DFAs.

❖      The complement of the language recognized by a given DFA.

Example

1. Q = {q0, q1, q2} 
2. ∑ = {0,1} 
3. q0 = {q0} 
4. F = {q2} 

Solution:

Transition Diagram :

Transition Table:

1.7 Simplified notation: State transition graph

A DFA A = (Q, Σ , δ, q0 ,F ) transition diagram is a graph that looks like this:

a. In Q, there is a node for each state.

b. Let q a p for each state q in Q and each input symbol a in ∑, let δ(q, a) = p.

The transition diagram thus displays a labeled arc from node q to node p. a If a number of input symbols induce transitions from q to p, the transition diagram can have a single arc labeled with the list of these symbols.

c. There is a labeled arrow into the initial state q0. Start This arrow does not start at any of the nodes.

d. A double circle denotes nodes that correspond to accepting states in F. There is just one c in states that are not in F.

A transition diagram, also known as a state transition diagram, is a directed graph that looks like this:

•    Each state in Q has a node, which is represented by the circle.

•    If δ (q, a) = p, there is a directed edge from node q to node p designated a.

•    There is an arrow with no source in the initial state.

•    A double circle indicates accepting states or final states.

Example: A string of letters and digits that starts with a letter can be defined as an identifier.

•    Token letter stands for any of the symbols a, . . . , z, A, . . . , Z.

•    The token digit represents 0, 1,..., 9.

The state-transition diagram in Figure defines the set of identifiers.

Fig: State -diagram for specifying identifiers

Example: The transition diagram for the DFA that we built in Example is shown in Figure. The three nodes that correspond to the three states can be seen in that diagram. The start state q1 is represented by a Start arrow, while the acceptance state q1 is represented by a double circle. Each state has one identified arc 0 and one labeled arc 1 (although the two arcs are combined into one with a double label in the case of q1). Each of the arcs corresponds to one of the facts that have been developed.

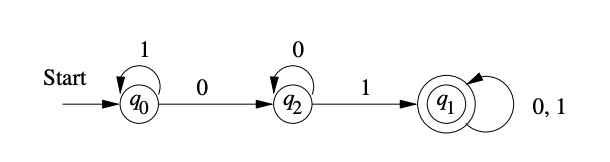
Fig: Transition diagram for DFA

1.8 Transition table

A transition table is a tabular representation of a function δ that accepts two inputs and returns a value, such as. The states are represented by the table's rows, while the inputs are represented by the table's columns. The state is the entry for the row that corresponds to state q and the column that corresponds to input δ (q, a).

The transition table is a table that shows how the transition function works. It takes two inputs (a state and a symbol) and outputs a state (the "next state").

The following elements make up a transition table:

•    The input symbols are represented by columns.

•    States are represented by rows.

•    The next state corresponds to the entries.

•    An arrow with no source denotes the initial state.

•    A star indicates the accept state.

Example: consider the below diagram

Solution: The following is the transition table for the given NFA:

The first row of the transition table reads: When the current state is q0, the next state on input 0 is q0, and the following state on input 1 is q1.

When the current state is q1, the next state will be either q1 or q2, and when the current state is q2, the following state will be q2.

When the current state is q2 on input 0, the following state is q1, and when the current state is q3 on input 1, the next state is q3.

When the current state is q3 on input 0, the following state is q2, and when the current state is q3 on input 1, the next state is q2.

1.9 Language of DFA

We can now define the notion of acceptance of a string, and thus acceptance of a language, in terms of a DFA.

If ˆδ (q0, x) ∈ F, a string x is said to be accepted by a DFA A = (Q, Σ, δ, q0, F). That is, the DFA will achieve a final state if the string x ∈ Σ ∗ is applied in the initial state.

The language accepted by A is defined as the set of all strings accepted by the DFA A and is denoted by L (A). That is to say,

L(A ) = {x ∈ Σ* | ˆδ(q0, x) ∈ F}

Example: Take into account the following DFA:

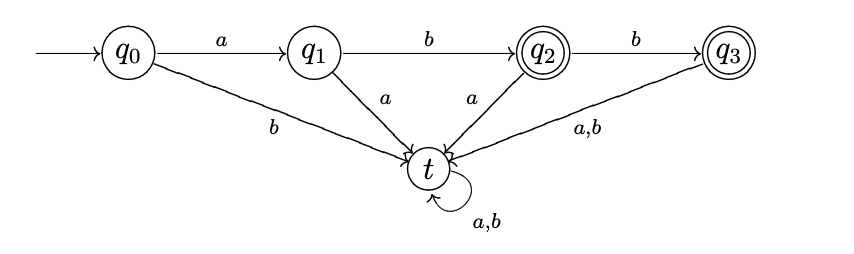The string ab is the only way to get from the beginning state q0 to the final state q2, and abb is the only way to get to another final state q3. As a result, the DFA's approved language is

{ab, abb}.

Example: Let us recollect the DFA's transition diagram, as given below.

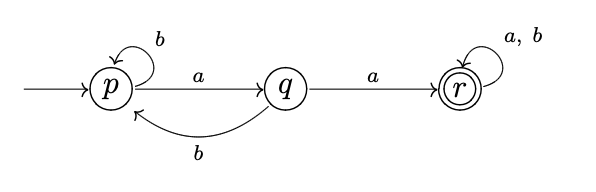
1. It’s important to remember that if the input contains aa, the DFA will take us from the starting state p to the final state r. Due to the fact that r is also a trap state, we will remain at r on any future input.

2. If there is no aa in the input, we will shuffle between p and q but never reach the ultimate state r.

As a result, the DFA accepts the set of all strings over a, b that have aa as a substring, i.e.

{xaay | x, y ∈ {a, b} *}.

1.10 Non-Deterministic Finite Automation (NFA)

In NDFA, the machine can move to any combination of the states. Hence, it is

Called Non-deterministic Automaton.

It has a finite number of states.

❖      Q → Finite non-empty set of states.

❖      ∑ → Finite non-empty set of input symbols.

❖      ∂ → Transitional Function.

❖      q0 → Beginning state.

❖      F → Final State

Transition function can be defined as:

δ: Q x ∑ →2Q

Graphical Representation of NFA

An NFA can be represented by digraphs called state diagram. In which:

1. The state is represented by vertices.
2. The arc labeled with an input character show the transitions.
3. The initial state is marked with an arrow.
4. The final state is denoted by the double circle.

Example

1. Q = {q0, q1, q2} 
2. ∑ = {0, 1} 
3. q0 = {q0} 
4. F = {q2}

Solution:

Transition Diagram:

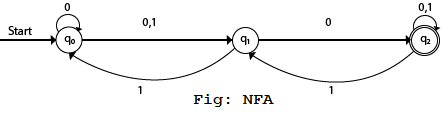
Transition table:

In this figure, we can see that the current state is q0 (input 0), and the next state will be q0, q1 (input 1) so the next state is q1. When the current state is q1 (input 0), the next state will be q2 (input 1), the next state is q0. When the current state is q2 (input 0), the next state is q2 (input 1), the next state will be q1 or q2.

1.11 NFA with epsilon transition

Epsilon closure for a given state X is a set of states which can be reached from the states X with only (null) or ε moves including the state X itself.  In other words, ε - closure for a state can be obtained by union operation of the ε - closure of the states which can be reached from X with a single ε move in recursive manner.

For the above example ∈ closures are as follows:

∈closure(A): {A, B, C}

∈closure(B): {B, C}

∈closure(C): {C}

Deterministic Finite Automata (DFA): DFA is a finite automata where, for all cases,

When a single input is given to a single state, the machine goes to a single state, i.e., all

The moves of the machine can be uniquely determined by the present state and the

Present input symbol.

Steps to Convert NFA with ε-move to DFA:

Step 1: Take ∈ closure for the beginning state of NFA as beginning state of DFA.

Step 2: Find the states that can be traversed from the present for each input symbol

(Union of transition value and their closures for each state of NFA present in current

State of DFA).

Step 3: If any new state is found take it as current state and repeat step 2.

Step 4: Do repeat Step 2 and Step 3 until no new state present in DFA transition table.

Step 5: Mark the states of DFA which contains final state of NFA as final states of DFA.

Transition state table for DFA corresponding to above NFA

DFA State diagram

1.12 Language of NFA

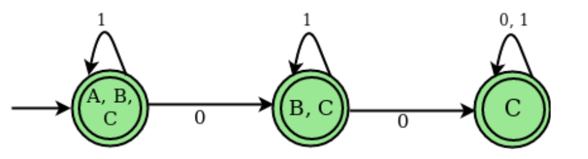
After reading the string entirely, a string is accepted by a DFA and the DFA, beginning at the initial state, ends in an accepting state (any of the final states).

A string S is accepted, if any, by the DFA (Q, ∑, δ, q0, F)

δ*(q0, S) ∈ F

The DFA-accepted language L is

{S | S ∈ ∑* and δ*(q0, S) ∈ F}

A DFA (Q, ∑ , δ, q0, F) does not accept a string S, if . .

δ*(q0, S′) ∉ F

The language L not recognized by the DFA/NDFA (Accepted language L complement) is.

{S | S ∈ ∑* and δ*(q0, S) ∉ F}

Example:

Let us take the DFA for consideration. The acceptable strings can be derived from the DFA.

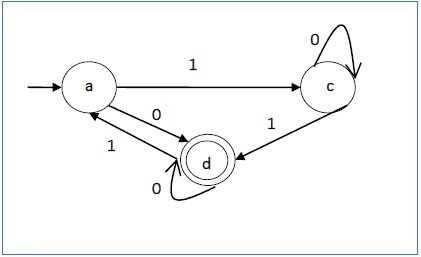
Strings that are approved by the above DFA: {0, 00, 11, 010, 101, ...........}

Strings which were not approved by the above DFA: {1, 011, 111, ........}

1.13 Equivalence of DFA and NFA

It would seem superficially that deterministic and non-deterministic finite state automata are totally distinct beasts. However, it turns out that they are equivalent. There is a DFA for every language recognized by an NFA that recognizes that language and vice versa.

The NFA to DFA conversion algorithm is relatively simple, even though the resulting DFA is substantially more complicated than the original NFA. I will illustrate this equivalence after the hop and also go through a brief example of converting an NFA to an equivalent DFA.

DFA and NFA Theorem proof -

Let's formally state the theorem we are proving before continuing:

Theorem:

Let the language L ⊆ Σ* be recognized by NFA N = (Σ, Q, q0, F, δ) and assume L.

A DFA D= (Σ, Q ', q'0, F', δ ') exists that also accepts L. (L(N)= L(D)).

We are able to prove by induction that D is equal to N by allowing each state in the DFA D to represent a set of states in the NFA N. Let's define the parameters of D: before we start proofing,

It's worth more explaining, I think δ '. Note that in the set of states Q 'in D, each state is a set of states from Q in N itself. Determine the transition δ (p, a) for each state p in state q in Q 'of D (p is a single state from Q). The union of all δ(q, a) is δ(q,a) .

Now we will demonstrate δ’(q0’, x) =δ’(q0 , x) that for every x  i.e. L(D) = L (N)

1.14 Minimization of Finite Automata

It is possible to create infinitely many finite state automata for a given regular language L to accept L. The answer is that there will be a loop in the transition diagram centered on a given DFA M1. To have more states and L(M1) = L(M2) = L, we can create a new DFA M2. And we can create a DFA M3 with even more states and L(M3) = L from DFA M2.

For instance, given a DFA M1, we can create a DFA M2 to have more states and

L(M1) = L(M2) = L.

Example: The following two DFA's are identical to M1 and M2. The collection above the alphabet Σ = {0,1} is accepted by {0n | n>0} both machines.

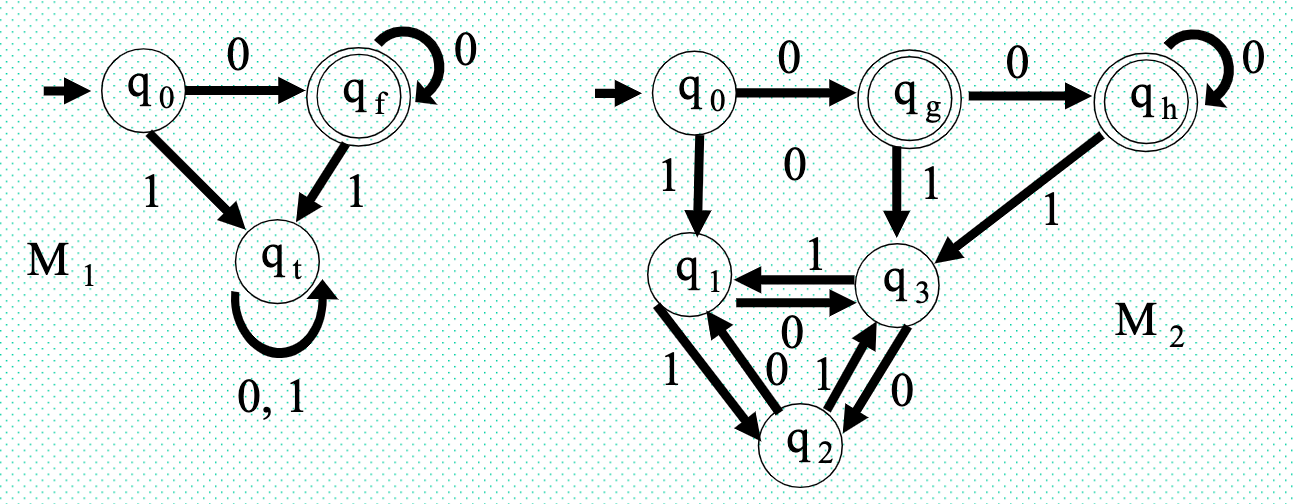
Machine M2 states q1, q2 and q3 are identical, we can combine these three states in one state as qt in machine M1.

The state qg and qh of the M2 machine are identical, these two states can be combined in one state as qf in the M1 machine.

1.15 Distinguishing one string from other

Consider the standard automaton, which accepts even-length strings over the alphabet {1} as an example. The transition function simply swaps states every time a character is read, and we have states qe (which is the start state and is accepting) and qo (which is not accepting). Every string greater than {1}*, including the empty string, distinguishes the two states for this automaton. Even-length strings (including) identify themselves because they are accepted by qe and refused by qo, but odd-length strings are the opposite.

1.16 Myhill- Nerode Theorem

The Myhill- Nerode language non-regularity test is based on the following theorem, which is in the contrapositive form of the theorem used for the non-regularity test. The Myhill- Nerode theorem is also a consequence:

Theorem: A language L over alphabet   is regular if and only if the set of equivalence classes of IL is finite.

Proof of Theorem -

Suppose L is a regular language and two strings, such as x and y, can be separated with respect to L. Then a string z is given so that xz is in L and yz is not in L (or xz is not in L and yz is in L). This means that the DFA enters various states if x and y are read by a DFA that recognizes L. If there are three strings that are separated with respect to L, then after reading those three strings, the DFA enters three distinct states....

Therefore, with respect to L, if there are infinitely many strings to be separated, then the DFA must have infinitely many states, which it cannot since a DFA must have a finite number of states.

Therefore, if there is an infinite set of strings that can be distinguished pairwise with regard to a language, then the language is not natural.

If, on the other hand, the number of string classes that are pairwise indistinguishable with respect to the L language is finite, the L language is normal.

To prove this, let [x] denote a class of strings that, with respect to L, are indistinguishable from string x. Note that 'indistinguishable from L' is an equivalence relationship over the   string set (refer to IL) and that [x]'s equivalence classes. We can demonstrate that using these equivalence groups, a DFA that accepts L can be built.

Myhill-Nerode Theorem

Let us state the Myhill-Nerode theorem here. Any terminology first.

For every x, y ∈  *, if x R y, then for every z ∈   *, xR y, then for every z ∈  *, xz R yz, an equivalence relationship R on  * is said to be the correct invariant.

If the set of its equivalence classes is finite, an equivalence relation is often said to be of a finite index.

With these words, it is now possible to state the Myhill-Nerode Theorem as follows:

The three sentences that follow are equivalent:

(1)  A language L is regular.

(2)  L is the union of some of the equivalence classes of a right invariant equivalent relation of finite index.

(3)   IL is of finite index.

References:

1.Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.

2.Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI

3.Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.