Unit - 2
Regular Expression (RE)
● Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.
● Regular languages are referred to as the languages recognized by certain regular expressions.
● A regular expression may also be defined as a pattern sequence that defines a series.
● For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.
A Regular Expression can be recursively defined as follows -
● ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})
● φ is a Regular Expression denoting an empty language. (L (φ) = { })
● x is a Regular Expression where L = {x}
● If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then
➢ X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
➢ X. Y is a Regular Expression corresponding to the language L(X). L(Y) where L (X.Y) = L(X). L(Y)
➢ R* is a Regular Expression corresponding to the language L(R*) where L(R*) = (L(R)) *
Example:
Write the regular expression beginning with a but not including consecutive b's for the language.
Sol: The regular expression has to be created for the language:
L = {a, aba, aab, aba, aaa, abab, ……}
Key takeaway
Simple expressions called Regular Expressions can readily define the language adopted by finite automata.
This is the most powerful way of expressing any language.
Regular expressions are used to produce patterns of strings, much as finite automata are used to recognize patterns of strings. A regular expression is an algebraic formula whose value is a pattern made up of a collection of strings known as the expression's language.
In a regular expression, the operands can be:
• The alphabetic characters that the regular expression is defined over.
• Any pattern defined by a regular expression can be used as a value for variables.
• epsilon, which stands for an empty string with no characters.
• The empty set of strings is denoted by null.
Regular expressions use the following operators:
Union - R1 | R2 (sometimes written as R1 U R2 or R1 + R2) is a regular expression if R1 and R2 are regular expressions.
L(R1|R2) = L(R1) U L(R2).
Concatenation - R1R2 (sometimes written as R1.R2) is a regular expression if R1 and R2 are regular expressions.
L(R1R2) = L(R1) concatenated with L(R2).
Kleene closure - R1* (the Kleene closure of R1) is a regular expression if R1 is a regular expression.
L(R1*) = epsilon U L(R1) U L(R1R1) U L(R1R1R1) U ...
Closure takes precedence over concatenation, which takes precedence over union.
Precedence
The regular-expression operators, like any algebra, have an assumed order of "precedence," which means that operators are associated with operands in a specific order. The following is the sequence of events:
1. The star operator is the most important.
2. The dot or concatenation operator is next.
3. Finally, all the unions (+) with their operands are gathered. (0(1) *) +1 is the grouping for the expression 01* +1.
In set notation, write the language L (a*. (a+b)).
L (a*. (a+b)) = L(a*) L(a+b)
= (L(a)) *(L(a)∪L(b))
= {ε, a, aa, aaa,….}{a,b}
= {a, aa, aaa, …, b, ab, aab, aaab,..}
Create a regular expression for the collection of strings that alternate between 0s and 1s.
Let's start by creating a single string 01. Regular expression for the language. The star operator may then be used to get an expression of all strings of the form 0101....0.
The RE base rule says that 0 and 1 are expressions that denote the languages 0 and 1, respectively. We get a regular expression for the language 01 by concatenating the two phrases; this is the expression 01.
Now we use the regular expression (01) * to get all strings with zero or more instances of 01, and we get L (01) *. However, because it only includes strings beginning with 0, this isn't exactly what we want. To account for strings beginning with 1 and strings ending with 0 or 1:
(01) * +(10) *+ 0 (10) *+ 1(01) *
Key takeaway
Regular expressions are used to produce patterns of strings, much as finite automata are used to recognize patterns of strings. A regular expression is an algebraic formula whose value is a pattern made up of a collection of strings known as the expression's language.
Let's look at the Regular Expression Algebraic Laws.
Associativity law
Let's look at the Regular Expression Associativity Laws.
A + (B + C) = (A + B) + C and A.(B.C) = (A.B).C.
Commutativity for regular expression
Let's look at the Regular Expression Commutativity Laws.
A + B = B + A. However, A.B 6= B.A in general.
Identity for regular expression
Let's look at the Regular Expression Identity.
∅ + A = A + ∅ = A and ε.A = A.ε = A
Distributivity
Let's look at the Regular Expression Distributivity.
Left distributivity: A.(B + C) = A.B + A.C.
Right distributivity: (B + C).A = B.A + C.A.
Idempotent A + A = A.
Closure laws
Let's look at the Regular Expression Closure laws.
(A*)* = A*, ∅* = ε, ε* = ε, A+ = AA* = A*A, and A* = A + + ε.
DeMorgan Type law
Let's look at the Regular Expression DeMorgan laws.
(L + B)* = (L*B*)*
Kleen’s theorem states that an FA accepts any regular language and, conversely, that any language that an FA accepts is regular.
Theorem 1: A finite automatic acknowledges every normal language.
Proof: The general induction following the recursive description of regular language would prove this.
Common step: The languages , {} and {a} for any symbol a in are accepted by an FA.
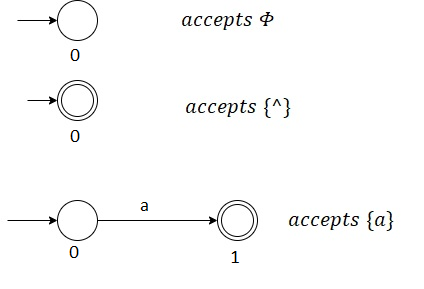
Example:
An NFA- that accepts the language represented by the regular expression is given - (aa + b)*
Sol: The given regular expression can be constructed using the operation, as below-
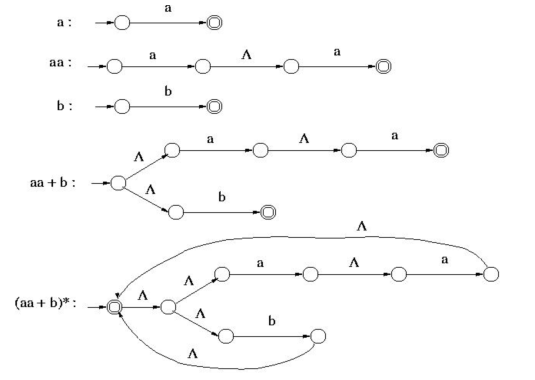
Fig: construction of (aa + b)*
Key takeaway
Kleen’s theorem states that an FA accepts any regular language and, conversely, that any language that an FA accepts is regular.
Regular expressions and finite automata have equivalent expressive power:
For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
For every FA, there is a corresponding regular expression that generates the
Set of strings accepted by A.
The proof is in two parts:
1. An algorithm that, given a regular expression R, produces an FA A such that L(A) == L(R).
2. An algorithm that, given an FA A, produces a regular expression R such that L(R) == L(A).
Our construction of FA from regular expressions will allow “epsilon transitions” (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols.
We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular expression.
If the operand is a character c, then our FA has two states, s0 (the start state)
And sF (the final, accepting state), and a transition from s0 to sF with label c.
If the operand is epsilon, then our FA has two states, s0 (the start state) and sF
(The final, accepting state), and an epsilon transition from s0 to sF.
If the operand is null, then our FA has two states, s0 (the start state) and sF (the
Final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and
R1*.
Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).
❏ The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.
❏ The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.
❏ The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.
Key takeaway
Regular expressions and finite automata have equivalent expressive power:
For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
Regular expressions and finite automata have equivalent expressive power:
● For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.
● For every FA, A there is a corresponding regular expression that generates the set of strings accepted by A.
The proof is in two parts:
1. An algorithm that, given a regular expression R, produces an FA A such that
L(A) == L(R).
2. An algorithm that, given an FA A, produces a regular expression R such that
L(R) == L(A).
Our construction of FA from regular expressions will allow “epsilon transitions” (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols. We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.
Constructing an FA from an RE
We begin by showing how to construct an FA for the operands in a regular
Expression.
● If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.
● If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.
● If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions.
Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and
R1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).
● The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.
● The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.
● The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.
Key takeaway
Our construction of FA from regular expressions will allow “epsilon transitions” (a transition from one state to another with epsilon as the label).
★ The Arden's Theorem is useful both for testing the equivalence of two regular phrases and for converting the DFA to a regular phrase.
★ In the conversion of DFA to a regular expression, let us see its use.
★ There are some algorithms used to build the regular expression form given in the DFA.
1. Let q1 be the initial state.
2. There are q2, q3, q4 .... Qn number of states. The final state may be some qj where j<= n.
3. Let αji represents the transition from qj to qi.
4. Calculate qi such that
qi = αji * qj
If qj is a start state then we have:
qi = αji * qj + ε
5. Similarly, compute the final state which ultimately gives the regular expression ‘r'.
Key takeaway
The Arden's Theorem is useful both for testing the equivalence of two regular phrases and for converting the DFA to a regular phrase.
The fact that regular languages of any alphabet are countable, and we know that the set of all subsets of strings is not countable, ensures the existence of non-regular languages. Nonetheless, the purpose of developing non-regular languages is to demonstrate that some languages that are "computable" in some sense are not regular.
Example: This is the non-regular example we'd want to show:
L = {w ∈ {a, b} *: w = aibi, for some i ≥ 0}
What is it about this language that makes it out of the ordinary? Consider the following string: w L. We'd have to keep track of how many a's we've seen and use that number to match off b's and accept if the numbers are equivalent. If we knew there were no more than 5 a's, we could use the following DFA (missing transitions lead to dead states):
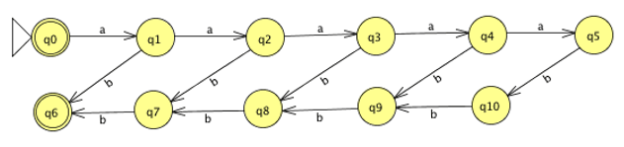
The difficulty is that we only have a finite amount of memory, thus we will eventually run out of a's to remember. The goal is to pinpoint the finite memory constraint. The traditional Pumping Lemma is used to do this.
Theorem -
Let L be a regular language. Then a constant c' exists such that for every string w in L
|w| ≥ c
We are able to split w into three strings, w=xyz, so that
● |y| > 0
● |xy| ≤ c
● For all k ≥ 0, the string xyKz is also in L.
Application of Pumping Lemma
It is important to apply Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.
● If L is regular, it satisfies Pumping Lemma.
● If L does not satisfy Pumping Lemma, it is non-regular.
Method for demonstrating that a language L is not regular
● We have to assume that L is regular.
● The pumping lemma should hold for L.
● Use the pumping lemma to obtain a contradiction −
● Select w such that |w| ≥ c
● Select y such that |y| ≥ 1
● Select x such that |xy| ≤ c
● Assign the remaining string to z.
● Select k such that the resulting string is not in L.
Therefore, L is not regular.
Example:
Prove that L = {aibi | i ≥ 0} is not regular.
Sol:
● At first, we assume that L is regular and n is the number of states.
● Let w = anbn. Thus |w| = 2n ≥ n.
● By pumping lemma, let w = xyz, where |xy| ≤ n.
● Let x = ap, y = aq, and z = arbn, where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.
● Let k = 2. Then xy2z = apa2qarbn.
● Number of as = (p + 2q + r) = (p + q + r) + q = n + q
● Hence, xy2z = an+q bn. Since q ≠ 0, xy2z is not of the form anbn.
● Thus, xy2z is not in L.
Hence L is not regular.
Regular languages are closed under a wide variety of operations.
Union and intersection –
Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection.
Set complement –
Pick a DFA recognizing the language, then swap the accept/non-accept markings on its states.
Set difference –
Rewrite set difference using a combination of intersection and set complement
Concatenation and Star –
Pick an NFA recognizing the language and modify it
Homomorphism –
A homomorphism is a function from strings to strings. What makes it a homomorphism is that it’s output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w: w = h(x) for some x in S}.
To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So, h(L) must also be regular.
Notice that regular languages are not closed under the subset/superset relation. For example, 0 * 1 * is regular, but its subset {O n 1 n: n > = 0} is not regular, but its subset {01,0011, 000111} is regular again.
If the language L of all yes instances to P is decidable, a decision problem P is said to be decidable (i.e., have an algorithm).
Example -
● (DFA acceptance problem) Provided that a DFA accepts a given problem, Word?
● Given a DFA, does it accept any word? (Emptiness problem for DFA)
● (DFA equivalence issue) Given two DFAs, do they accept the DFA problem? Language of the same?
Problem: Some of regular L1 and L2 languages, the problem is whether or not there is a string 'w' in both L1 and L2, a deciding problem.
Sol: Firstly, two Turing TM1 and TM2 machines simulate the DFAs of the L1 and L2 languages, respectively. We know a DFA always stops, so a Turing machine that simulates a DFA will always stop, too. In TM1 and TM2 we join the string 'w'. The two Turing machines are going to halt and give us an answer.
We may connect the Turing machine outputs to a modified 'AND' gate that will only output 'yes' when both Turing machines respond to 'yes'. Otherwise, 'no' is production.
This problem is a deciding problem, as this system of two Turing machines and a changed AND gate will always stop.
Key takeaway
If the language L of all yes instances to P is decidable, a decision problem P is said to be decidable (i.e., have an algorithm).
● A Finite Automation has a finite number of states and is also called as Finite State Machine (FSM).
● FA (finite automata) is used for recognition patterns.
● FA have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reaches its final state, then it will accept.
Moore Machine
The Moore machine is a finite state machine in which the current state and the current input symbol define the next state. At a given time, the output symbol depends only on the machine's current state.
Moore machine can be described by 6 tuples (Q, q0, ∑, O, δ, λ) where,
- Q: finite set of states
- q0: initial state of machine
- ∑: finite set of input symbols
- O: output alphabet
- δ: transition function where Q × ∑ → Q
- λ: output function where Q → O
Example:
The state diagram for Moore Machine is-
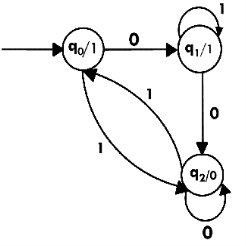
Transition Table for MM (Moore Machine) is
Current State | Next State(δ) | Output(λ) | |
0 | 1 | ||
q0 | q1 | q2 | 1 |
q1 | q2 | q1 | 1 |
q2 | q2 | q0 | 0 |
Mealy Machine
A Mealy Machine is a machine in which the output symbol depends on the machine's current input symbol and current state. The output is expressed in the Mealy machine with each input symbol for each state, separated by /.
The Mealy machine can be described by 6 tuples (Q, q0, ∑, O, δ, λ') where
- Q: finite set of states
- q0: initial state of machine
- ∑: finite set of input alphabet
- O: output alphabet
- δ: transition function where Q × ∑ → Q
- λ': output function where Q × ∑ →O
Key takeaway
The Moore machine is a finite state machine in which the current state and the current input symbol define the next state. At a given time, the output symbol depends only on the machine's current state.
A Mealy Machine is a machine in which the output symbol depends on the machine's current input symbol and current state. The output is expressed in the Mealy machine with each input symbol for each state, separated by /.
Moore and the Mealy machine appear differently from each other. Designing a Moore machine with a mealy machine is often possible. Designing a mealy machine with a Moore machine is often possible. It is possible to transform any Moore machine into a mealy machine. Moore machine or mealy machine may be used to describe each standard language. All languages specified by a mealy machine or Moore machine are standard.
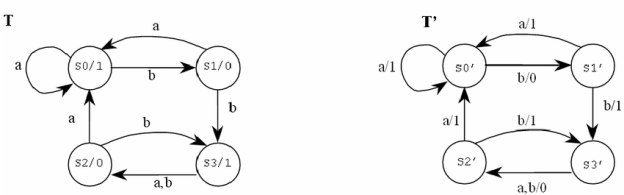
Fig: Example of equivalent Moore and mealy machine
A Moore machine M can never be correctly equal to a mealy machine M 'since one greater than that of the mealy machine M' on the same input is the length of the output string of a Moore machine M.
We can, however, overlook the reaction of the Moore machine to input λ and say for all inputs w, Moore machine M and a mealy machine M 'are equivalent if
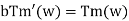
Where b for its initial state is the output of the Moore machine M
Theorem: If M1= (Q, Σ, Δ, δ, λ, q0) is a Moore machine then there is an M2 equivalent to M1 mealy machine.
Proof: Create a mealy machine M2 as (Q, Σ, Δ, δ, λ’, q0)
λ’ is describe as-
λ’(q, a) = λ(δ (q, a)) For q and input symbols of all states a
Moore machine is on input 1010 output
0 1 2 2 1
Although the output from the mealy machine constructed is
1 2 2 1
By the equivalence state
In the beginning of output of Mealy machine, we can add output of q0 0 of Moore machine.
The machine generated is therefore equivalent to the Moore machine defined.
Key takeaway
Moore and the Mealy machine appear differently from each other. Designing a Moore machine with a mealy machine is often possible. Moore machine or mealy machine may be used to describe each standard language.
Application of FA
• For the creation of a compiler's lexical analysis.
• Regular expressions are used to recognize the pattern.
• Mealy and Moore Machines are used to design combination and sequential circuits.
• In text editors, this term is used.
• In order to install spell checkers.
Limitation of FA
• Only finite input can be counted by FA.
• There is no finite auto ma that can locate and recognize a set of binary strings containing the same number of Os and 1s.
• Set of strings with balanced parenthesis over "(" and ")".
• The input tape is read-only, and the only memory available is state-to-state.
• Only a string pattern is allowed.
• There is just one way to move your head.
References:
1.Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.
2.Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI
3.Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.