Unit – 3

Context Free Grammar (CFG) and Context Free Languages (CFL)

3.1 Definition

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

It consists of:

❏      A set of terminal symbols,

❏      A set of non-terminal symbols,

❏      A set of productions,

❏      A start symbol.

Context-free grammar G can be defined as:

G = (V, T, P, S)

Where 

G - grammar, used for generate string,

V - final set of non-terminal symbol, which are denoted by capital letters,

T - final set of terminal symbols, which are denoted be small letters,

P - Set of production rules, it is used for replacing non terminal symbol of a string in both side (left or right)

S - Start symbol, which is used for derive the string

A CFG for Arithmetic Expressions -

An example grammar that generates strings representing arithmetic expressions with the four operators +, -, *, /, and numbers as operands is:

1. <expression> --> number

2. <expression> --> (<expression>)

3.<expression> --> <expression> +<expression>

4. <expression> --> <expression> - <expression>

5. <expression> --> <expression> * <expression>

6. <expression> --> <expression> / <expression>

The only non-terminal symbol in this grammar is <expression>, which is also the

Start symbol. The terminal symbols are {+, -, *, /, (,), number}

❏      The first rule states that an <expression> can be rewritten as a number.

❏      The second rule says that an <expression> enclosed in parentheses is also an <expression>

❏      The remaining rules say that the sum, difference, product, or division of two <expression> is also an expression.

Key takeaway

Context-free grammar (CFG) is a collection of rules (or productions) for recursive rewriting used to produce string patterns.

3.2 Examples

Example 1:

Construct a CFG for a language with any number of a's in the set ∑= {a}.

Solution:

The regular expression for the above language is, as we know:

r.e. = a*     

The following is the Regular expression's production rule:

S → aS    rule 1  

S → ε     rule 2  

We may now start with start symbols to derive the string “aaaaaa”:

S  

AS   

AaS          rule 1  

AaaS         rule 1  

AaaaS        rule 1  

AaaaaS       rule 1  

AaaaaaS      rule 1  

Aaaaaaε      rule 2  

Aaaaaa  

The r.e. = a* can generate a set of string {ε, a, aa, aaa,.....}. We can have a null string because S is a start symbol and rule 2 gives S → ε.

Example 2:

Construct a CFG for a language L = {wcwR | where w € (a, b)*}.

Solution:

The string that can be generated for a given language is {aacaa, bcb, abcba, bacab, abbcbba, ….}

The grammar could be as follows:

S → aSa     rule 1  

S → bSb     rule 2  

S → c       rule 3  

We may now start with start symbols to generate the string "abbcbba."

S → aSa   

S → abSba       from rule 2  

S → abbSbba     from rule 2  

S → abbcbba     from rule 3  

As a result, any string of this type can be produced from the stated production rules.

3.3 Derivation

Derivation is the collection of rules for development. Via these production laws, it is used to get the input string. We have to take two decisions during parsing.

These are as follows:

We have two options to decide which non-terminal to be placed with production rule

1. Leftmost Derivation:

The input is scanned and replaced by the production rule from left to right in the left-most derivation. So, we read the input string from left to right in the left-most derivation.

Example:

➢      Produle rule -

P = P + P

P = P - P

P = a | b

➢      Input -

a - b + a

➢      Leftmost derivation is:

P = P + P 

P = P - P + P

P = a - P + P

P = a - b + P 

P = a - b + a

2.     Rightmost Derivation:

The input is scanned and replaced by the production rule from right to left in the right-most derivation. So, we read the input string from right to left in the right-most derivation.

Example:

➢      Produle rule -

P = P + P

P = P - P

P = a | b

➢      Input -

a - b + a

➢      Rightmost Derivation is -

P = P - P 

P = P - P + P 

P = P - P + a 

P = P - b + a 

P = a - b + a 

We can receive the same string when we use the leftmost derivation or rightmost derivation.

Note -

The reception of a string does not affect this method of derivation.

3.4 Derivation Trees and Ambiguity

The tree of derivation is a graphical representation of the derivation for a given CFG of the development rules given. It is the easy way to explain how to extract any string from a given set of production rules to obtain the derivation.

The parse tree follows the operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.

A parse tree contains the following properties:

1. The root node is always a node indicating start symbols.
2. The derivation is read from left to right.
3. The leaf node is always terminal nodes.
4. The interior nodes are always the non-terminal nodes.

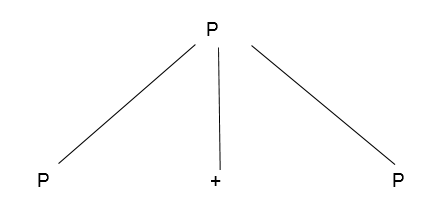
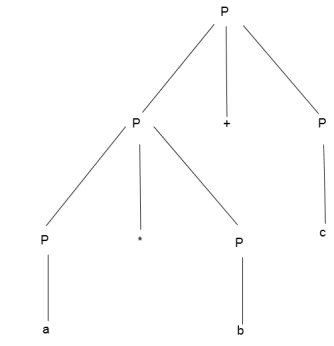
Example:

Production rule:

1. P = P + P 
2. P = P * P 
3. P = a | b | c

Input:

a * b + c 

Step 1 -   

Step 2 -

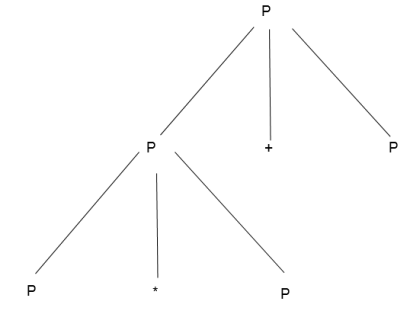
Step 3 -

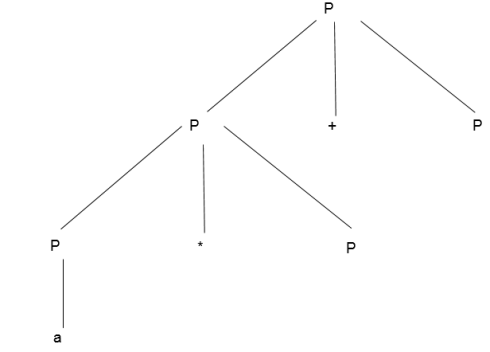
Step 4 -

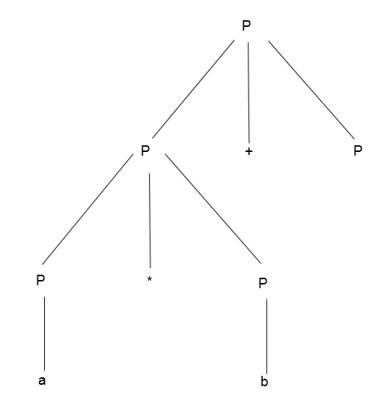
Step 5 -

Ambiguous Context Free Languages:

If there is no unambiguous grammar to describe the language and it is often called necessarily ambiguous Context Free Languages, a context free language is called ambiguous.

Key takeaways:

❖      Language generated by grammar L(G) may or may not be ambiguous if a context-free grammar G is ambiguous.

❖      Ambiguous CFG will not always be translated to unambiguous CFG. It is possible to convert just some ambiguous CFG to unambiguous CFG.

❖      There is no algorithm to convert ambiguous CFG to unambiguous CFG.

❖      There always exists an unambiguous CFG corresponding to unambiguous CFL.

❖      Deterministic CFL are always unambiguous.

3.4 Inherent ambiguity

Rohit Parikh proved the existence of intrinsically ambiguous languages using Parikh's theorem in an MIT research report in 1961.

While certain context-free languages (the set of strings that a grammar can create) have both ambiguous and unambiguous grammars, there are some context-free languages for which there is no unambiguous context-free grammar. The union of {an bm cm dn | n,m  > 0} with {an bn cm dm | n,m  > 0} is an example of intrinsically confusing language.

Because the union of two context-free languages is always context-free, this set is context-free. However, Hopcroft and Ullman (1979) show that there is no method to parse strings in the (non-context-free) common subset {an bn cn dm | n > 0} unambiguously.

3.5 Ambiguous to Unambiguous CFG

We may eliminate ambiguity merely based on the following two characteristics –

1. Precedence

If multiple operators are employed, the precedence of the operators will be taken into account. The following are the three most crucial characteristics:

1. The priority of the operator used is determined by the level at which the production is present.
2. Operators with lower priority will be assigned to higher-level production. The lower priority operators will be found in the top layers or near to the root node of the parse tree.
3. Operators with higher priority will be assigned to lower-level production. The higher priority operators will be found in the nodes at lower levels or near to the leaf nodes in the parse tree.

2. Associativity

If the same precedence operators are used in production, the associativity must be considered.

1. If the associativity is left to right, the production must urge a left recursion. The parse tree will be recursive and grow on the left side as well. +, -, *, / are left associative operators.

b.   If the associativity is right to left, the right recursion in the productions must be prompted. The parse tree will grow on the right side and be right recursive. ^ is a right associative operator.

Example:

Take a look at the unclear grammar.

E -> E-E | id

The language in the grammar will contain {id, id-id, id-id-id, ….}

Let's say we're trying to deduce the string id-id-id. To gain further insight, consider a single value of id=3. As a result, you should be able to say:

3 - 3 - 3 = - 3

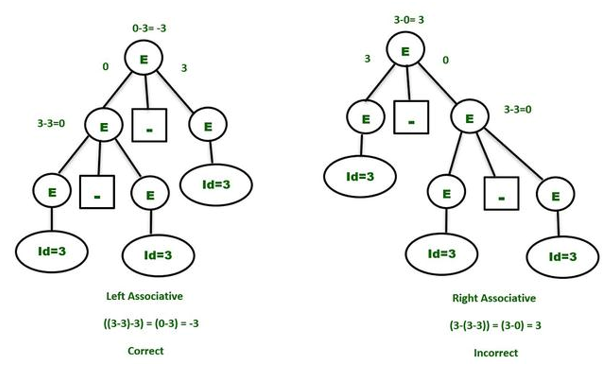
We must consider associativity, which is left to right, because the priority operators are the same.

Parse tree - In order to make the grammar unambiguous, the parse tree that grows on the left side of the root will be the correct parse tree.

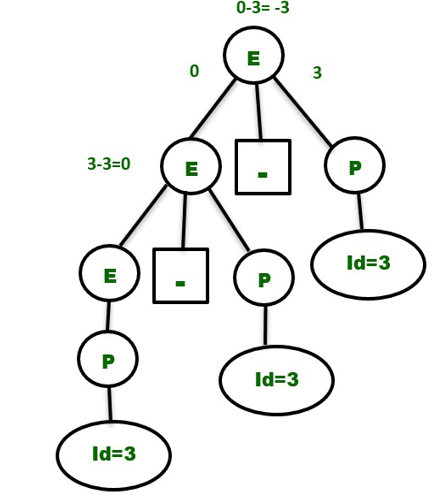
Simply make the grammar Left Recursive by substituting the left most non-terminal E in the right side of the production with another random variable, say P, to make the above grammar clear. The grammar is changed to:

E -> E – P | P

P -> id

The above grammar is now clear, and the above phrase will only have one Parse Tree, as seen below —

Similarly, given the expression: 2^3^2, the unambiguous grammar will be –

E -> P ^ E | P         // Right Recursive as ^ is right associative.

P -> id

3.6 Useless symbols

If a variable X in a context-free grammar does not appear in any derivation of a word from that grammar, it is said to be useless.

This is a simple algorithm for removing superfluous variables from CFGs.

If a variable generates a string of terminals, call it generating. It's worth noting that a context-free grammar accepts language that isn't empty if and only if the start sign is generated. An algorithm for locating the generating variables in a CFG is as follows:

1. If a variable X has a production X -> w, where w is a string of solely terminals and/or variables already tagged "producing," mark it as “generating."
2. Repeat the previous step until no more variables are designated as “producing.”

All variables that aren't labeled "generating" are non-generating variables (by a simple induction on the length of derivations).

If the start symbol yields a string containing the variable, call it accessible. Here's how to identify the variables that can be reached in a CFG:

Assign the status "reachable" to the start variable.

1. If there is a production X -> w, where X is a variable previously tagged as "reachable" and w is a string containing Y, mark a variable Y as “reachable."

2.  Repeat the last step until no more variables are identified as "reachable."

All variables that aren't labeled "reachable" are unavailable (by a simple induction on the length of derivations).

Keep in mind that a CFG only has no useless variables if and only if all of its variables are reachable and producing.

As a result, it is possible to remove unnecessary variables from a grammar in the following way:

1. Find and eliminate all non-generating variables, as well as any productions involving non-generating variables.

2.  Find and delete any non-reachable variables in the resulting grammar, as well as all products that use non-reachable variables.

Step 1 does not make other variables non-generating or non-reachable, and step 2 does not make other variables non-generating or non-reachable. As a result, the end result is a grammar that is reachable and generates all variables, making it usable.

Key takeaway

If a variable X in a context-free grammar does not appear in any derivation of a word from that grammar, it is said to be useless.

This is a simple algorithm for removing superfluous variables from CFGs.

3.7 Simplification of CFG

As we have included a context-free grammar can effectively represent different languages. Not all grammar is always optimized, which means that there might be some extra symbols in the grammar (non-terminal). Unnecessary change in the length of grammar with additional symbols.

Here are the properties of reduced grammar:

1. Every parameter (i.e., non-terminal) and every terminal of G occurs in the derivation of any word in L.
2. As X→Y where X and Y are non-terminal, there should not be any output.
3. If ε is not in the L language, then the X→ ε output does not have to be.

Let’s see the simplification process

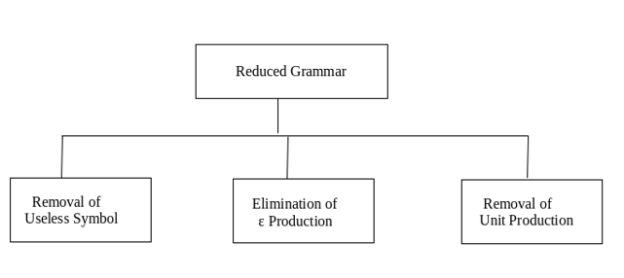
Fig: Simplification process

• Removal of Useless Symbols - A symbol can be useless if it does not appear on the right-hand side of the production rule and is not involved in the derivation of any string.  The symbol is regarded as a symbol which is useless. Likewise, if it does not participate in the derivation of any string, a variable may be useless. That variable is called a useless symbol.
• Elimination of ε Production - The Type S → ε productions are called ε productions. Only those grammars which do not produce ε can be excluded from these types of output.

Step 1: First find out all nullable non-terminal variables which derive ε.

Step 2: Create all output A → x for each production A →a where x is extracted from a by removing one or more non-terminals from step 1.

Step 3: Now combine with the original output the outcome of step 2 and delete ε productions.

Example:  Remove the production from the given CFG

1. E → XYX 
2. X → 0X | ε 
3. Y → 1Y | ε

Solution:

Now, we remove the rules X → ε and Y → ε while removing ε production. In order to maintain the sense of CFG, whenever X and Y appear, we actually position ε on the right-hand side.

Let’s see

If the 1st X at right side is ε, then

E → YX

Similarly, if the last X in right hand side is ε, then

E → XY

If Y = ε, then

E → XX

If Y and X are ε then,

S → X

If both X are replaced by ε

E → Y 

Now,

E → XY | YX | XX | X | Y

Now let us consider

X → 0X 

If we then put ε for X on the right-hand side,

X → 0

X → 0X | 0 

Similarly, Y → 1Y | 1

Collectively, with the ε output excluded, we can rewrite the CFG as

E → XY | YX | XX | X | Y 

X → 0X | 0 

Y → 1Y | 1

Removing unit production - Unit productions are those productions in which another non-terminal generates a non-terminal one.

To remove production unit, follow given steps: →

Step 1: To delete X → Y, when Y→ a occurs in the grammar, apply output X → a to the grammar law.

Step 2: Remove X → Y from the grammar now.

Step 3: Repeat steps 1 and 2 until all unit output is deleted.

Example:

1. E → 0X | 1Y | Z 
2. X → 0E | 00 
3. Y → 1 | X 
4. Z → 01

Sol:

E → Z is a unit production. But while removing E → Z, we have to consider what Z gives. So, we can add a rule to E.

E → 0X | 1Y | 01 

Similarly, Y → X is also a unit production so we can modify it as

Y → 1 | 0S | 00 

Finally, then without unit manufacturing, we can write CFG as

E → 0X | 1Y | 01 

X → 0E | 00 

Y → 1 | 0S | 00 

Z → 01 

Key takeaways:

-         Grammar simplification means reducing grammar by the elimination of useless symbols.

-         Simplification process contains three major parts.

-         Removal of useless symbol, Elimination of ε production, Removing unit production

3.8 Normal forms for CFGs: CNF and GNF

Chomsky Normal Form (CNF)

The Chomsky normal form (CNF) is a context free grammar (CFG) if all output rules satisfy one of the conditions below:

Consider the following grammars,

G1 = {S->a, S->AZ, A->; a, Z->z}

G2 = {S->a, S->aZ, Z->a}

As production rules comply with the rules defined for CNF, the grammar G1 is in CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Greibach Normal Form (GNF)

If the productions are in the following forms, a CFG is in the Greibach Normal Form -

A → b

A → bD 1 …D n

S → ε

Where A, D 1, ...., D n are non-terminals and b is a terminal.

Algorithm to Convert a CFG into Greibach Normal Form

Step 1 − If the starting symbol S is on the right side, create a new starting symbol.

S 'symbol and a new S'→ S output.

Step 2 − Remove Null productions.

Step 3 − Remove unit productions.

Step 4 − Delete both left-recursion direct and indirect.

Step 5 − To transform it into the proper form of GNF, make proper output substitutions.

Example:

Convert the following CFG into CNF

S → XY | Xn | p

X → mX | m

Y → Xn | o

Sol:

Here, S does not appear on the right side of any production and in the production rule collection, there is no unit or null output. So, we'll be able to bypass step 1 to step 3.

Step 4 -Now after replacing

X in S → XY | Xo | p

With

MX | m

We obtain

S → mXY | mY | mXo | mo | p.

And after replacing

X in Y → X n | o

With the right side of

X → mX | m

We obtain

Y → mXn | mn | o.

The production set is added to two new productions O → o and P → p and then we arrived at the final GNF as the following -

S → mXY | mY | mXC | mC | p

X → mX | m

Y → mXD | mD | o

O → o

P → p

Key takeaway –

CNF is a pre-processing step used in various algorithms.

For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.

3.9 Closure properties of CFLs

They are closed under −

●      Union

●      Concatenation

●      Kleene Star operation

Union of the languages A1 and A2, A = A1 A2 = {anbncmdm}

The additional development would have the corresponding grammar G, P:  S → S1 S2

Union

Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.

Example

Let A1 = {xn yn, n ≥ 0}. Corresponding grammar G 1 will have P: S1 → aAb|ab

Let A2 = {cm dm, m ≥ 0}. Corresponding grammar G 2 will have P: S2 → cBb| ε

Union of A1 and A2, A = A1 ∪ A2 = { xn yn } ∪ {  cm dm  }

The corresponding grammar G will have the additional production S → S1 | S2

Note - So under Union, CFLs are closed.

Concatenation

If A1 and A2 are context free languages, then A1 A2 is also context free.

Example

Union of the languages A 1 and A 2, A = A 1 A 2 = {an bn cm dm}

The corresponding grammar G will have the additional production S → S1 S2

Note - So under Concatenation, CFL are locked .

Kleene Star

If A is a context free language, so that A* is context free as well.

Example

Let A = {xn yn, n ≥ 0}. G will have corresponding grammar P: S → aAb| ε

Kleene Star L 1  = { xn yn  }*

The corresponding grammar G 1 will have additional productions S1 → SS 1 | ε

Note - So under Kleene Closure, CFL's are closed .

Context-free languages are not closed under −

●      Intersection − If A1 and A2 are context free languages, then A1 ∩ A2 is not necessarily context free.

●      Intersection with Regular Language − If A1 is a regular language and A2 is a context free language, then A1 ∩ A2  is a context free language.

●      Complement − If A1  is a context free language, then A1’ may not be context free.

3.10 Decision Properties of CFLs: Emptiness, Finiteness and Membership

•    It is possible to determine whether or not a CFG G is empty.

•    The following questions are undecidable?

•    Testing the membership of a string w in a CFG G is also decidable.

1. Is there any ambiguity in a particular G?

2. Is a CFL by definition ambiguous?

3. Is the point where two CFLs meet empty?

4. Is there a difference between two CFLs?

3.11 Pumping lemma for CFLs

Lemma: The language L = 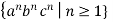 is not context free.

Proof (By contradiction)

Assuming that this language is context-free; hence it will have a context-free grammar.
Let K be the constant of the Pumping Lemma.

Considering the string 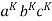, where L is length greater than K.
By the Pumping Lemma this is represented as 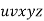, such that all 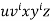are also in L, which is not possible, as:

Eithe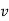r  nor 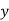   cannot contain many letters from 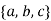; else they are in the wrong order.

If 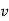 or 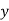   consists of a's, b's or c's, then 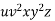cannot maintain the balance amongst the three letters.

Lemma: The language L = 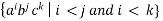is not context free.

Proof (By contradiction)

Assuming that this language is context-free; hence it will have a context-free grammar.

Let K be the constant of the Pumping Lemma.

Considering the string 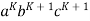, which is L > K.

By the Pumping Lemma this must be represented as 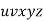, such that all  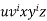are also in L.

-As mentioned previously neither  nor   may contain a mixture of symbols.

-Suppose 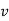 consists of a's.

Then there is no way 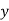 cannot have b's and c's.  It generates enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
Similarly 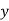 cannot consist of just a's.

-So suppose then that 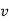 or 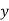 contains only b's or only c's.
Consider the string 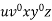 which must be in L. Since we have dropped both  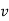and 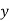, we must have at least one b' or one c' less than we had in 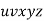, which was 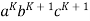. Consequently, this string no longer has enough of either b's or c's to be a member of L.

References:

1.Introduction to Automata Theory, Languages, and Computation, 2e by John E, Hopcroft, Rajeev Motwani, Jeffery D. Ullman, Pearson Education.

2.Theory of Computer Science (Automata, Languages and Computation), 2e by K. L. P. Mishra and N. Chandrasekharan, PHI

3.Harry R. Lewis and Christos H. Papadimitriou, Elements of the Theory of Computation, Pearson Education Asia.