Unit – 2
Intermediate Code Generation
A simple block DAG is a directed acyclic graph containing the following labels on nodes:
● DAGs are a type of structure for data. It is used on simple blocks to execute transformations.
● A good way to decide a common sub-expression is given by DAG.
● This provides an image of how the value determined by the argument is used in subsequent statements.
Algorithm for construction of DAG
Input: It contains a basic block
Output: It contains the details given below:
● A label is embedded in every node. For leaves, an identifier is the name.
● A list of attached identifiers for keeping the computed values is stored in each node.
Case (i) x: = y OP z
Case (ii) x: = OP y
Case (iii) x: = y
Method
Step 1:
If the operand of y is undefined, create a node (y).
If z operand is undefined, build a node for Case(i) (z).
Step 2:
Construct node (OP) for case(i), whose right child is node(z) and whose left child is node(y).
Check if there is a node (OP) with one child node (y) for case(ii).
Node n will be the node (y) for case(iii).
Output
For node(x), remove x from the ID list. Append x to the list of attached identifiers for the n node listed in step 2. Third, set node(x) to n.
Example:
Find the following three statements of address:
S1: = 4 * i
S2: = a[S1]
S3: = 4 * i
S4: = b[S3]
S5: = s2 * S4
S6: = prod + S5
Prod: = s6
S7: = i+1
i: = S7
if i<= 20 goto (1)
Stages in DAG Construction:
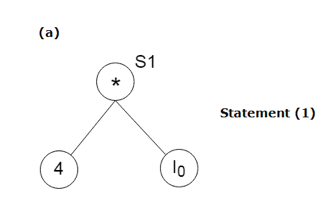
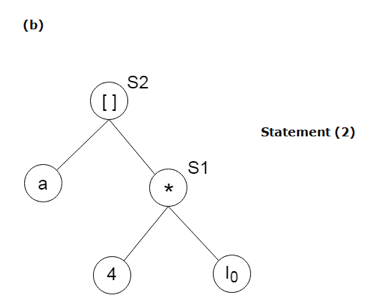
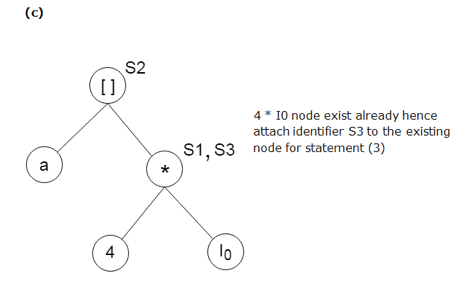
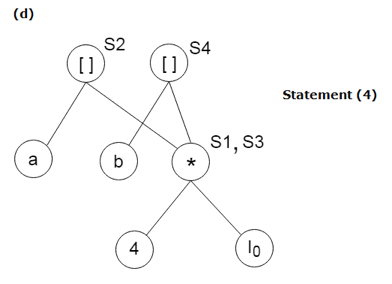
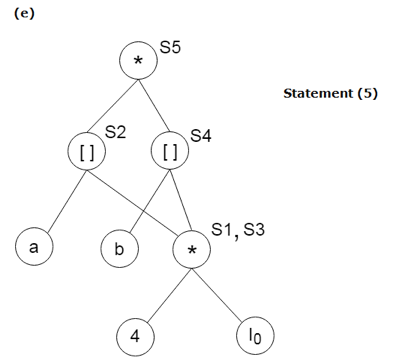
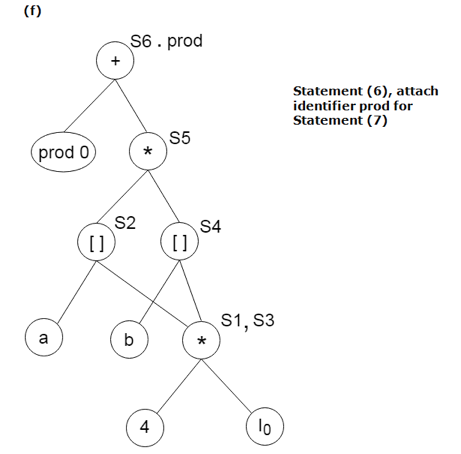
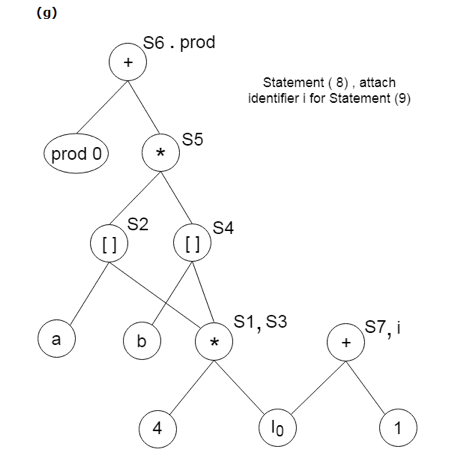
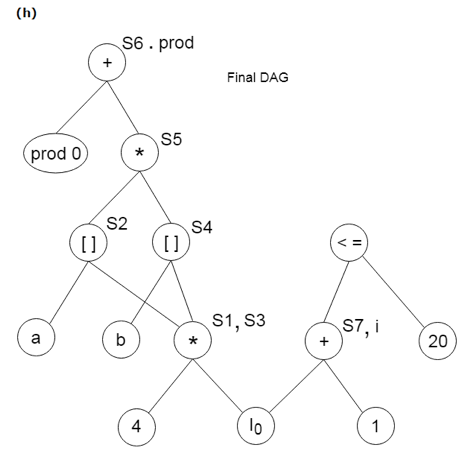
Key takeaway:
An intermediate code is a three-address code. It is used by the compilers that optimize it. The provided expression is broken down into multiple separate instructions in the three-address code. Such instructions can be easily translated into the language of assembly.
Any instruction for the three address codes has three operands at most. It is a combination of a binary operator and a mission
The compiler defines the order of operation generated by three code addresses.
General representation:
x = y op z
Where x, b or c represents temporary generated operations such as names, constants or compiler and op represents the operator.
Example
Given expression:
w: = (-y * x) + (-y * z)
The code with three addresses is as follows:
t1: = -y
t2: = x *t1
t3: = -y
t4: = z * t3
t5: = t2 + t4
w: = t5
It is used as registers in the target programme.
It is possible to represent the three address codes in two forms: quadruples and triples.
Quadruple & triples
Quadruple
For the implementation of the three address codes, the quadruples have four fields. The quadruple field includes the name of the generator, the first operand source, the second operand source, and the output, respectively
Operator |
Argument 1 |
Argument 2 |
Destination |
Fig: quadruple field
Example
w: = -x * y + z
The code with three addresses is as follows:
t1: = -x
t2: = y + z
t3: = t1 * t2
w: = t3
These statements are expressed as follows by quadruples:
| Operator | Source 1 | Source 2 | Destination |
(0) | uminus | x |
| t1 |
(1) | + | y | z | t2 |
(2) | * | t1 | t2 | t3 |
(3) | := | t3 |
| w |
Triples
For the implementation of the three-address code, the triples have three fields. The area of triples includes the name of the operator, the first operand of the source and the second operand of the source.
The outcomes of the respective sub-expressions are denoted by the expression location in triples. Although describing expressions, Triple is equal to DAG.
Operator |
Argument 1 |
Argument 2 |
Fig: Triples field
Example:
w: = -x * y + z
The three code addresses are as follows:
t1: = -x
t2: = y + zM
t3: = t1 * t2
w: = t3
Triples represent these statements as follows:
| Operator | Source 1 | Source 2 |
(0) | uminus | x |
|
(1) | + | y | z |
(2) | * | (0) | (1) |
(3) | := | (2) |
|
Key takeaway:
We need to lay out storage for the declared variables when we encounter declarations.
You can manage declaration with a list of names as follows:
D T id; D | ε
T B C | record ‘{‘D’}’
B int | float
C ε | [ num] C
We create a ST (Symbol Table) entry for every local name in a procedure, containing:
Production:
D → integer, id
D → real, id
D → D1, id
For declarations, an appropriate transformation scheme would be:
Production rule | Semantic action |
D → integer, id | ENTER (id.PLACE, integer) D.ATTR = integer |
D → real, id | ENTER (id.PLACE, real) D.ATTR = real |
D → D1, id | ENTER (id.PLACE, D1.ATTR) D.ATTR = D1.ATTR |
ENTER is used to enter the table of symbols and ATTR is used to trace the form of data.
Key takeaway:
In the syntax directed translation, the assignment statement mainly deals with expressions. The expression can be of type real, integer, array and records.
Consider the grammar
The translation scheme of above grammar is given below:
Production rule | Semantic actions |
S → id: =E | {p = look_up(id.name); If p ≠ nil then Emit (p = E.place) Else Error; } |
E → E1 + E2 | {E.place = newtemp(); Emit (E.place = E1.place '+' E2.place) } |
E → E1 * E2 | {E.place = newtemp(); Emit (E.place = E1.place '*' E2.place) } |
E → (E1) | {E.place = E1.place} |
E → id | {p = look_up(id.name); If p ≠ nil then Emit (p = E.place) Else Error; } |
● The p returns the entry for id.name in the symbol table.
● The Emit function is used for appending the three-address code to the output file. Otherwise, it will report an error.
● The newtemp () is a function used to generate new temporary variables.
● E.place holds the value of E.
● Array elements can be accessed easily if elements are stored in a sequential position block.
● Elements are numbered 0,1,.........,n-1(n elements) for an array.
● If the width of each element of an array is w, the ith element of array A starts at position
Base + i * w
Where base - relative address, define storage allocation.
(Base is relatively address of A [0])
● The array may be one- or two-dimensional.
For one - dimensional array:
A: array [low. high] of the ith elements is at:
base + (i-low) *width → i*width + (base - low*width)
For multi - dimensional array:
Row major or column major forms
● Row major: a [1,1], a [1,2], a [1,3], a [2,1], a [2,2], a [2,3]
● Column major: a [1,1], a [2,1], a [1, 2], a [2, 2], a [1, 3], a [2,3]
● In row major form, the address of a [i1, i2] is
● Base+((i1-low1) *(high2 - low2+1) +i2-low2) *width
Layout for 2D array:

Fig 3: two-dimensional array
Key takeaway:
A compiler must check that the source program follows both syntactic and semantic conventions of the source language. This checking, called static checking, detects and reports programming errors.
Some examples of static checks:
1. Type checks - A compiler should report an error if an operator is applied to an incompatible operand. Example: If an array variable and function variable are added together.
2. Flow-of-control checks - Statements that cause flow of control to leave a construct must have some place to which to transfer the flow of control. Example: An enclosing statement, such as break, does not exist in switch statements.
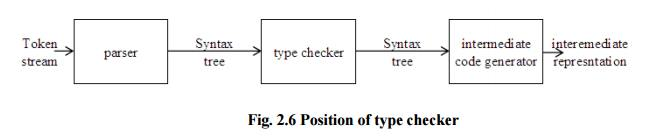
Fig: position of type checker
A type checker verifies that the type of a construct matches that expected by its context. For example: arithmetic operator mod in Pascal requires integer operands, so a type checker verifies that the operands of mod have type integer. Type information gathered by a type checker may be needed when code is generated.
Type Systems
The design of a type checker for a language is based on information about the syntactic constructs in the language, the notion of types, and the rules for assigning types to language constructs.
For example: “if both operands of the arithmetic operators of +, - and * are of type integer, then the result is of type integer”
Type Expressions
The type of a language construct will be denoted by a “type expression.” A type expression is either a basic type or is formed by applying an operator called a type constructor to other type expressions. The sets of basic types and constructors depend on the language to be checked. The following are the definitions of type expressions:
1. Basic types such as boolean, char, integer, real are type expressions.
A special basic type, type_error, will signal an error during type checking; void denoting “the absence of a value” allows statements to be checked.
2. Since type expressions may be named, a type name is a type expression.
3. A type constructor applied to type expressions is a type expression.
4. Type expressions may contain variables whose values are type expressions.
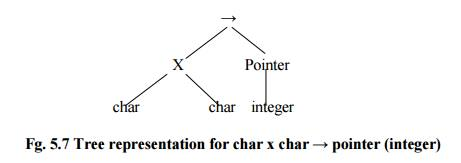
Fig: tree representation for char x char → pointer (integer)
Type systems
A type system is a collection of rules for assigning type expressions to the various parts of a program. A type checker implements a type system. It is specified in a syntax-directed manner. Different type systems may be used by different compilers or processors of the same language.
Static and Dynamic Checking of Types
Checking done by a compiler is said to be static, while checking done when the target program runs is termed dynamic. Any check can be done dynamically, if the target code carries the type of an element along with the value of that element.
Conversions
● Expression X + I (The X is real and I is int type)
● First compiler check both of the operand are of same type or not
● Usually convert int type into real type and perform real operand operation
How to Convert
● X + I (int convert into real)
● X I intoreal real +
● Intoreal operation convert I intoreal
● Or real+ operation perform real addition in between both real operands
Coercions
● Convert one type to another automatically called implicit or coercions like ASCII
● It is limited in many languages in case of no information loss
● Integer convert into real but no vice versa because of some memory loss
● When programmer write something to convert called Explicit
Overloading Functions
● The same name is used for several different operations over several different types.
● Type checker is used to detect the error while creating overloading functions
Polymorphic Functions
● A piece of code that can be executed with arguments of different types
Key takeaway:
Boolean expressions have two primary purposes.
1. They are used for computing the logical values.
2. They are also used as conditional expressions that alter the flow of control, such as if-then-else or while-do.
Boolean expressions are composed of the boolean operators (and, or, and not) applied to elements that are boolean variables or relational expressions. Relational expressions are of the form E1 relop E2, where E1 and E2 are arithmetic expressions.
Consider the grammar
E → E or E
E → E and E
E → not E
E → (E)
E → id relop id
E → TRUE
E → id
E → FALSE
The relop is any of <, ≤, =, ≠, >, or ≥. We assume that or and are left associative. or has lowest precedence, then and, then not.
Methods of Translating Boolean Expressions:
There are two methods of representing the value of a Boolean.
1.To encode true or false numerically
• 1 is used to denote true.
• 0 is used to denote false.
2.To evaluate a boolean expression analogously to an arithmetic expression.
• Flow of control –representing the value of a boolean expression by a position reached in a program.
• Used in flow of control statements such as if-then-else or while-do statements.
Numerical Representation of Boolean Expressions:
First consider the implementation of boolean expressions using 1 to denote TRUE and 0 to denote FALSE. Expressions will be evaluated from left to right.
Example 1:
A or B and C Three address sequence:
T1 = B and C
T2 = A or T1
Example 2:
A relational expression A< B is equivalent to the conditional statement. if A < B then 1 else 0
Three address sequence:
(1) if A < B goto (4)
(2) T=0
(3) goto (5)
(4) T=1
(5) ---
Semantic Rules for Boolean Expression:
The Semantic rules for Boolean expression are given as below:

Example: Code for a < b or c < d and e <f
100: if a < b goto 103
101: t1 = 0
102: goto 104
103: t1 = 1
104: if c < d goto 107
105: t2 =0
106: goto 108
107: t2 = 1
108: if e < f goto 111
109: t3 =0
110: goto 112
111: t3 = 1
112: t4 = t2 and t3
113: t5 = t1 or t4
Control Flow Representation:
Short Circuit Evaluation of Boolean Expressions: Flow of control statements with the jump method.
Consider the following: (short circuit code)
S → if E then S | if E then S1 else S2
S → while E do S1
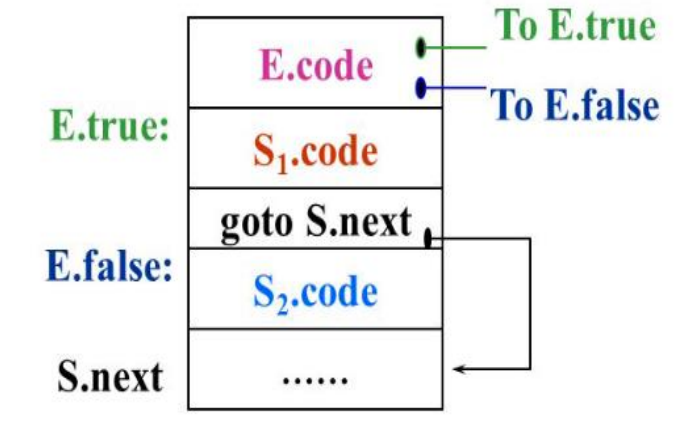
Fig: attribute used for if E then S1 else S2
E is associated with two attributes:
1. E.true: label which controls if E is true
2. E.false : label which controls if E is false
S.next - is a label that is attached to the first three address instruction to be executed after the code for S (S1 or S2)
The Semantic rule for flow of control statements is given by:
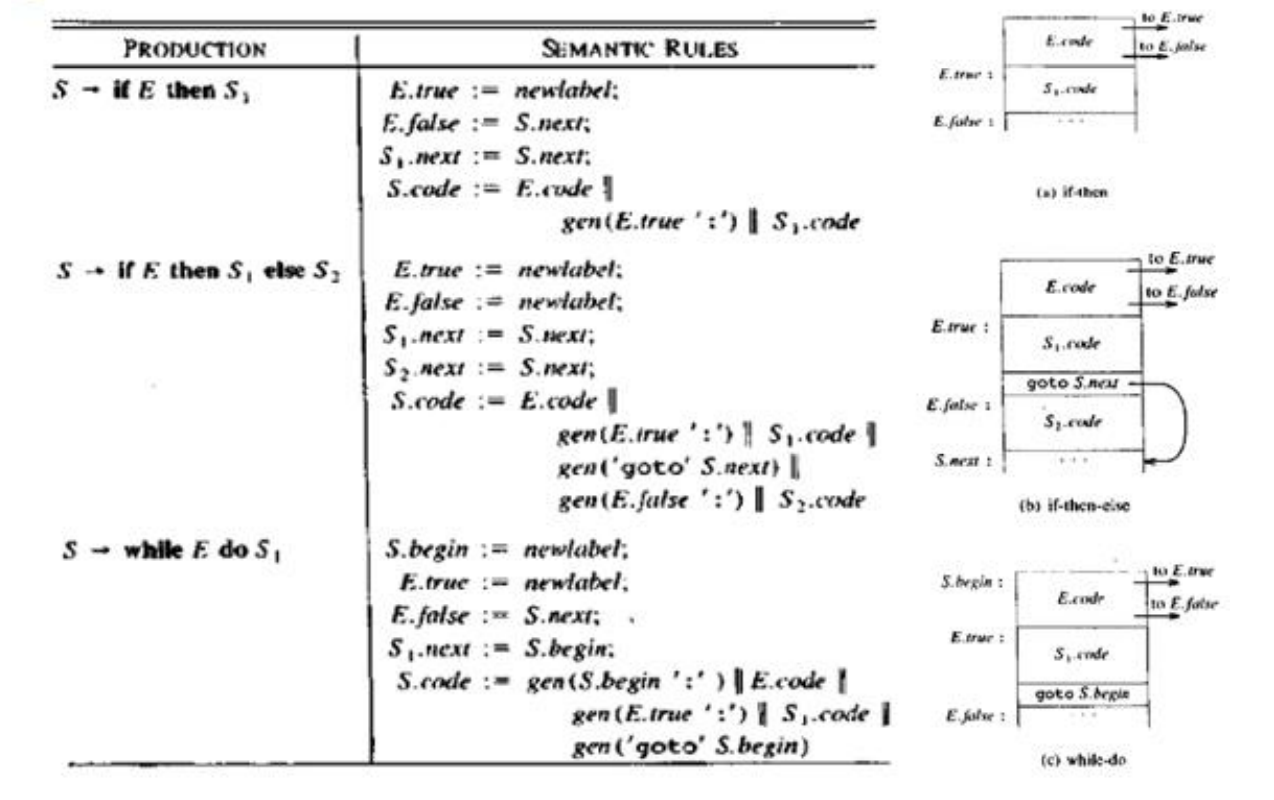
Fig: semantic rule for control statements
Key takeaway:
All labels cannot be recognized in a single pass in the code generation process (primarily, 3 Address Code), so we use a technique called Backpatching.
Backpatching is the task of filling in unspecified label information during the code generation process using acceptable semantic behaviour.
Three functions are used to implement the backpatching technique. The three functions performed in two passes to create code using backpatching are Makelist(), merge() and backpatch().
Three kinds of operations are carried out by Backpatching Algorithms
Here ‘p’ is the pointer to any statement say p=> “if a<b goto ____”.
Initially, we don’t know the label to fill just after goto.
After backpatch(p,i)
p=>“if a<b goto i”
Key takeaway:
In order to convert the source code into the computer code, intermediate code is used. Between the high-level language and the computer language lies the intermediate code.

Fig: position of intermediate code generator
● If the compiler converts the source code directly into the machine code without creating intermediate code, then each new machine needs a complete native compiler.
● For all compilers, the intermediate code holds the research section the same, which is why it does not require a complete compiler for each specific machine.
● Input from its predecessor stage and semantic analyzer stage is obtained by the intermediate code generator. This takes feedback in the form of an annotated tree of syntax.
● The second stage of the compiler synthesis process is modified according to the target machine by using the intermediate code.
Intermediate representation:
It is possible to represent the intermediate code in two ways:
The intermediate code of the high level can be interpreted as the source code. We can easily add code modifications to boost the performance of the source code. Yet there is less preference for optimizing the goal machine.
2. Low level intermediate code:
The low-level intermediate code is similar to the target computer, making it ideal for registering and allocating memory, etc. It is used for optimizations depending on the machine.
Key takeaway:
References: