Unit - 2
Standard test signals
The Impulse signal, Ramp signal, unit step and parabolic signals are used as the standard test signals. All these signals are explained below.
Impulse Signal: -
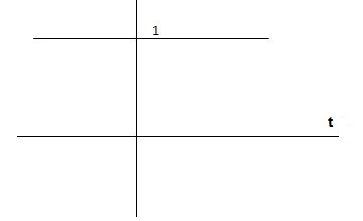
This signal has zero amplitude everywhere except at the origin. Fig below shown the representation of Impulse signal.
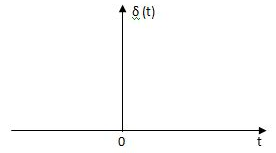
Fig 1 Unit Impulse Signal
The mathematical representations
A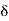 (t) = 0 for t ≠0
(t) = 0 for t ≠0
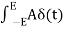 dt = A e
dt = A e 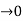
Where A represent energy or area of the Laplace Transform of Impulse signal is
L [A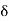 (t)] = A
(t)] = A
UNIT IMPULSE SIGNAL: -
If A = 1
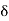 (t) = 0 for t ≠0
(t) = 0 for t ≠0
L [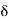 (t)] = 1
(t)] = 1
The transfer function of a linear time invariant
System is the Laplace transform of the impulse response of the system. If a unit impulse signal is applied to system, then Laplace transform of the output c(s) is the transfer function G(s)
As we know G(s) = c(s)/R(S)
r(t) = 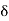 (t)
(t)
R(s) = L [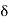 (t)] = 1
(t)] = 1
:. G(S) = C(s)
(b) Step signal: -
Step signal of size A is a signal that change from zero level to A in zero time and stays there forever.
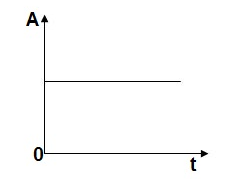
Fig 2 Unit Step Signal
r(t)= A t >=0
=0 t<0
L[r(t)] = R(s) = A/s
UNIT STEP SIGNAL: - If the magnitude of the slip signal is I then it is called unit step signal.
u(t) = 1
t>=0
t<0
L[u(t)] = 1/s
(c) Ramp Signal: -
The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
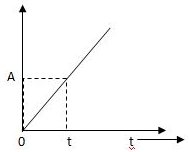
Fig 3 Ramp Signal
r(t) = At t>=0
=0 t<0
A is the slope of the line The Laplace transform of ramp signal is
L[r(t)] = R(s) = A/s2
(d) Parabolic Signal: -
The instantaneous value of a parabolic signal varies as square of the time from an initial value of zero t=0. The signal representation in fig 14 below.
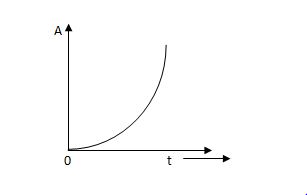
Fig 4 Parabolic Signal
r(t) At2 t>=0
=0 t<0
Then Laplace Transform is given as
R(s) = L[At2] = 2A/s3
If no error then E(t) =0, R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 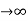 )
)
Ess = t 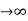 e(t)
e(t)
Using final values, the theorem
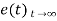 = ess =
= ess = 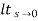 S.E (s)
S.E (s)
ess= 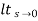 S[R(s)/1+G/(s)]
S[R(s)/1+G/(s)]
Key takeaway
If no error then E(t) =0, R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 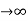 )
)
Ess = t 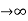 e(t)
e(t)
Using final values, the theorem
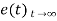 = ess =
= ess = 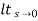 S.E (s)
S.E (s)
Transient Analysis of First Order System:
OLTF G(s) = 1/TS
CLTF c(s)/R(s) = 1/1+TS
CE: HTS = 0
S= -1/T
C(s) = R(s) [G(S)/1+G(s)]
C(s) = R(s)/1+TS
So, Calculating value of c(s), c(t) for different input
a) Unit Step:
R(t) = u(t)
R(s) = 1/s
C(s) = 1/s(1+ST)
1/s(1+ST) = A/s + o/1+TS
1/s(1+ST) = A/S + 0/1+TS
1= A(1+ST) + BS
AT +B =0
A = 1
B= -T
C(s) = 1/s + (-T)/1+TS
= 1+ (-T)/1-(-T) s = 1-I/n/1+ass+1/T =e-t/s
C(t) = [ 1-e-t/T]
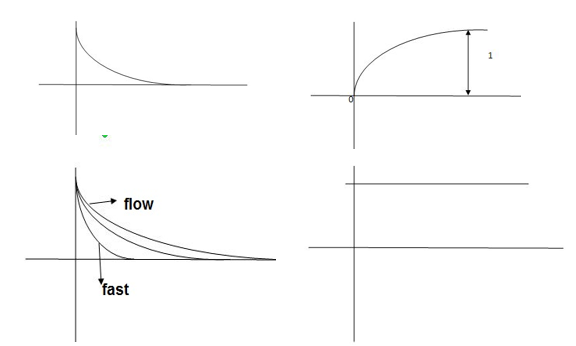
Fig 5 Output response for Unit Step input
Ramp:
R(t) = t
R(s) = 1/s2
C(s) = R(s) [G(s)/1+G(s)]
C(s) = 1/s2 1/(1+TS) + c
1/s2 (1+TS) = A/(s) + B/s2 + c(1+TS)
1 = A (s+s2. T) + B(1+TS) +cs2
TA +c = 0
A+TB =0
B =1
A = -T
C = T2
C(s) = -T/s + 1/s2 +T2/1+ST
=(-T) u(t) + t(u) + T e-t/T u(t)
= [ -T + t +Te-t/T u(t)
= [ -T+ t+Te-t/T] u(t)
C(s) = t- T+ Te-t/T
ess = 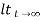 R(t) – c(t)
R(t) – c(t)
=  [ t- t+ 7-Te –t/T]
[ t- t+ 7-Te –t/T]
= 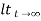 T( 1-e-t/T]
T( 1-e-t/T]
ess = The less the value of T the less in the errors.
Fig 6 Output response for ramp input
From both the Cases input unit step, ramp Unit step
Unit Step Ramp
c(t) = 1-e-t/T r(t) = t
ess = e-t/T (r/t)-(t) c(t) = t- T+te-t/T
ess= e-t/T (r/t) (t) ess = T- Te-t/T
For :- for
:- for :-
:-
ess =0 ess = T
1) In both the vases (values of T) must be as small as possible (so, that e-t/T) must be as small as possible which gives us
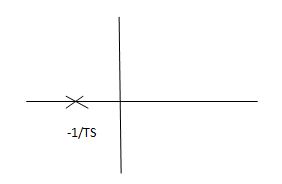
Fig 7 Location of poles
G(s) = 1/Ts
ATf = 1/1+TS
1st order system
Poles must be situated as far as possible from origin i.e., deeper and deeper into the left half of s-place. Thus, we get less errors.
Transient Analysis of Second Order System:
OLTF G(s) = k/s(1+TS)
CLTFC(s)/R(s) = k/k+s(1+Ts)
= k/s2+ s/T +k/T
Comparing above equation with standard 2nd order eqn
CLTF = wn2/s2+2rs wns+wn2
CEs2+2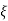 wn s+wn2= 0
wn s+wn2= 0
S= -2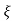 wn±
wn±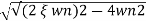 /2
/2
=2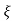 wn±2wn
wn±2wn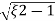 /2
/2
S=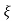 wn±wn
wn±wn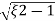
S= -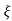 wn±wn
wn±wn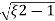
S= -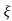 wn ±wn
wn ±wn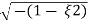
S= -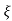 wn ±gwn
wn ±gwn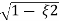
Standard eqn:
T(s) = wn2/s2+2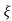 wns+wn2
wns+wn2
Our eqn T(s) = K/T/s2+1/T s+ K/T
Wn2 = k/T
2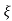 wn = 1/T
wn = 1/T
2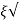 k/T = 1/T
k/T = 1/T
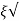 k/T = 1/2T
k/T = 1/2T
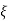 = 1/2T
= 1/2T 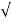 T/K
T/K
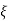 = 1
= 1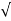 2KT
2KT
Graphically showing the position of loops s1, s2 for offered of
As the characteristic Eqn. (location of poles) is dependent only on (wn constant for a given system)
S1 = -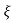 wn + jwn
wn + jwn 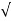 1-
1-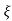 2
2
S2= -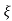 wn - jwn
wn - jwn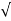 1-
1-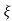 2
2
CASE 1: (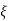 =0)
=0)
S1=jwn, S2, = -jwn
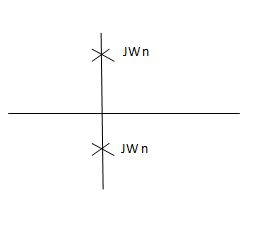
Fig 8 Location of poles for 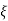 =0
=0
Undamped
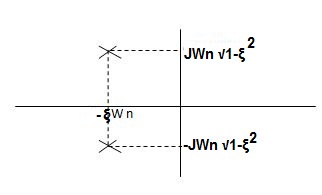
CASE 2:(0<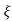 <1)
<1)
S1= -wn + jwn 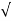 0.75
0.75
=-wn/2 +jwn (0.26)
S2 = -wn/2 – jwn (0.86)
Fig 9 Location of poles for  <1
<1
CASE:3 ( =1)
=1)
S1= S2 = -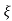 wn = -wn
wn = -wn
Fig 10 Location of poles for  =1
=1
CASE4: ( =-2)
=-2)
S1 = -2wn +jwn 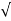 -3
-3
=-2wn – jwn (1.73)
S1= -3.73wn
S2 = -2wn –jwn 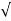 -3
-3
= -2wn + jwn (1.73)
= -0.27 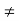 wn
wn
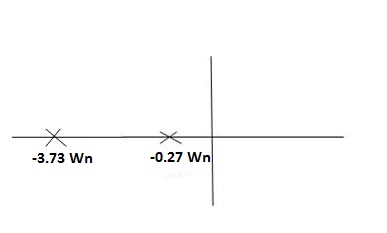
Fig 11 Location of poles for 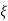 >1
>1
Overdamped
Key takeaway
All practical systems are 2 order to, if R(e) = 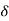 (t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
(t) R(s) = 1. CLTF = 2nd order st eqn and hence already the system is possible.
CLTF = e(s)/ R(s) = wn2/s2+2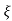 wns+wn2
wns+wn2
Now calculating c(s), c(t) for different values of input
1) Impulse I/p
R(t) = 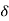 (t)
(t)
R(s) = 1
C(s) = R(s) wn2/s2+2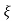 wns+wn2
wns+wn2
C(s) = wn2/s2 +2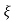 wn+wn2
wn+wn2
Under this i/p (R(t) = 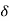 (t)) the output varies with different values of
(t)) the output varies with different values of 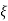 . So,
. So,
CONDITION 1: (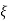 =0)
=0)
C(s) =wn2/s2 +wn2
Os2 +wn2 =0
S=+-jwn
C(t) = wn sinwnt
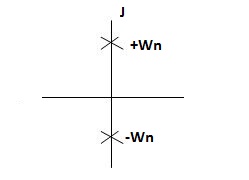
Sinwnt
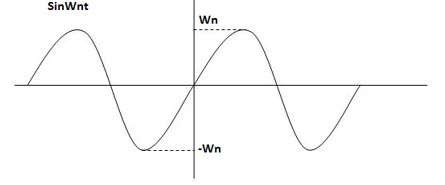
Fig 12 Undamped oscillations
As there in no damping i.e. oscillations at t= 0 are some at t  so, called UNDAMPED
so, called UNDAMPED
CONDITION 2: 0<<1
c(s) = R(s) wn2/s22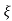 wn+wn2 R(t) =
wn+wn2 R(t) = 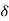 (t)
(t)
R(s) =1
C(s) = wn2/s2+2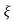 wns+wn2
wns+wn2
CE
S2+2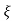 wns +wn2 =0
wns +wn2 =0
S2, S1 = -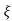 wn ±jwn
wn ±jwn 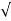 1-
1-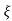 2
2
C(t) = e-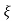 wnt sin (wn
wnt sin (wn 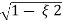 )t
)t
Wd=wn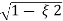 )
)
C(t)=e-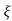 wnt sin (wdt)
wnt sin (wdt)
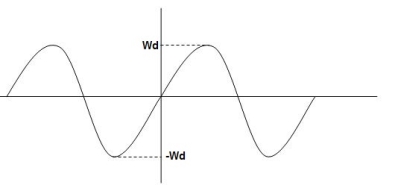
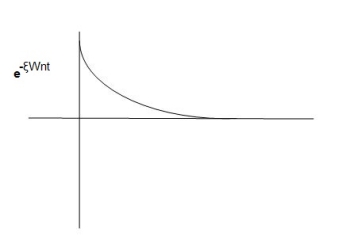
Fig 13 Underdamped oscillations
The oscillations are present but at t- infinity the Oscillations are 0 so, it is UNDERDAMPED
CONDITION 3: 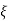 =1
=1
C(s) = R(s) wn2/s2+2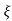 wns+wn2
wns+wn2
C(s)=wn2/S2 +2wns+wn2
=wn2/(s +wn)2
CE S= -Wn
Diagram
C(t)=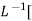 w2n /(
w2n /(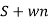 )2
)2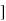
C(t)=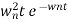
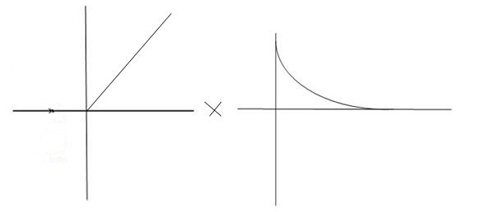
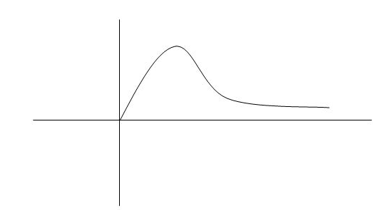
Fig 14 Critically damped oscillations
No damping obtained at 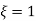 so is called CRITICALLY DAMPED.
so is called CRITICALLY DAMPED.
CONDITIONS 4: >1
>1
C(s) = wn2/s22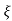 wnS+Wn2
wnS+Wn2
S1, s2 = 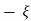 WN+-jwn
WN+-jwn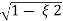
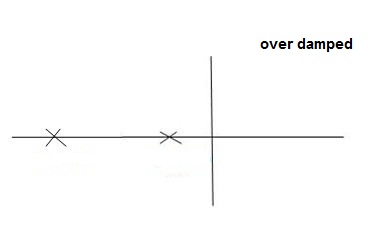
Fig 15 location of poles for over damped oscillations
b) UNIT Step Input:
R(s) = 1/s
C(s)/R(s) = wn2/s2+2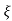 wns+wn2
wns+wn2
C(s) = R(s) wn2 /s2 +2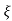 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2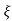 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2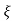 wns+wn2
wns+wn2
C(s) = wn2s(s2+2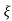 wns+wn2)
wns+wn2)
C(t) = 1- e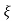 wnt/
wnt/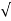 1-es2 sin (wdt + ø)
1-es2 sin (wdt + ø)
Wd = wn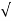 1-
1-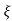 2
2
Ø= 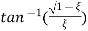
Where
Wd = Damping frequency of oscillations
Wn = natural frequency of oscillations
 wn = damping coefficient.
wn = damping coefficient.
T= Time constant
Condition 1 = 0
= 0
C(s) = wn2 /s(s2+wn2)
C(t) = 1- e° sin wdt +ø
C(t)= 1- sin(wn +90)
C(t) = 1+cos wnt
Constant
C(t) = 1+constant
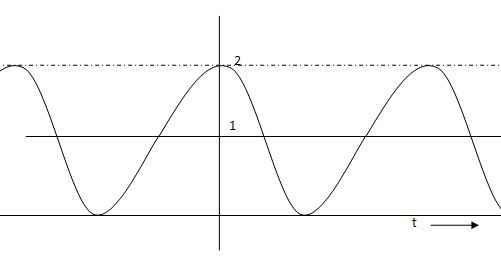
Fig 16 C(t) = 1+cos wnt
Condition 2: 0<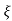 <1
<1
C(s) = 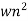 /s2+
/s2+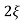 wns +wn2
wns +wn2
C(s) =1/s – s+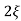 wn/s2+
wn/s2+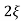 wns +wn2
wns +wn2
=1/s – s+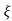 wn/(s+
wn/(s+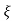 wn)2+wd2-
wn)2+wd2- 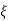 wn/(s+
wn/(s+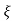 wn2) +wd2
wn2) +wd2
Wd = wn 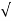 1-
1-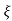 2
2
Taking Laplace inverse of above equation
L --1 s+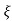 wn/(s+
wn/(s+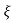 wn) +wd2= e-
wn) +wd2= e-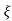 wnt cos wdt
wnt cos wdt
L-1 s+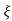 wn/(s+
wn/(s+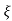 wn)2+wd2 = e-
wn)2+wd2 = e-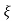 wnt sinWdt
wnt sinWdt
C(t) = 1-e-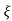 wnt [coswdt +
wnt [coswdt +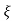 /
/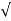 1-
1-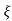 2 sinwdt]
2 sinwdt]
= 1-e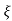 wnt /
wnt /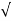 1-
1-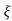 2 sin [wdt +
2 sin [wdt + 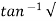 1-
1-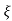 2/
2/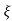 ] t>=0
] t>=0
C(t) = 1-e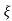 wnt/
wnt/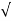 1-
1-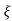 2 sin(wdt+ø)
2 sin(wdt+ø)
Ø = 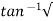 1+
1+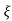 2/
2/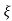
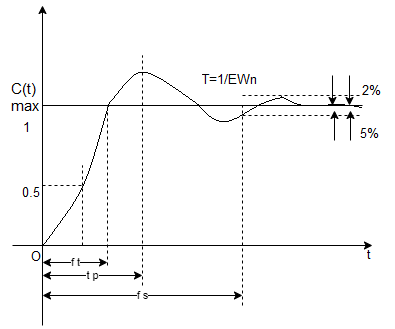
Fig 17 Transient Response of second order system
Q1) Find the initial value for the function f(t) = 2u(t)+3cost u(t)?
Sol:
f(t) = 2u(t)+3cost u(t)
F(s) = 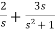
SF(s) = 2+ 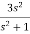
By initial value theorem
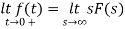 = f(0+)
= f(0+)
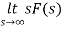 =
= 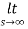 2+
2+ 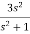 = 5 = f(0+)
= 5 = f(0+)
Hence, initial value of the function is 5
Q2) Find final value of the function F(s) = 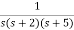
Sol:
F(s) = 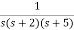
SF(s) = 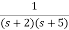
By final value theorem
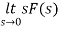 =
= 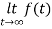
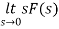 =
= 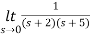 = 0.1
= 0.1
So, final value of the function is 0.1
Key takeaway
By initial value theorem
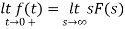 = f(0+)
= f(0+)
By final value theorem
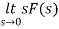 =
= 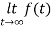
Specifications:
1) Rise Time (tp): The time taken by the output to reach the already status value for the first time is known as Rise time.
C(t) = 1-e-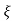 wnt/
wnt/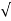 1-
1-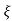 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n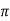
tr =n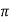 -ø/wd
-ø/wd
For first time so, n=1.
tr = 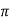 -ø/wd
-ø/wd
T=1/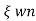
Peak Time (tp)
The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n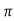 /wd for n=1
/wd for n=1
tp = 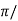 wd
wd
3) Peak Overshoot Value:
Maximum deviation of output from steady state value is called peak overshoot value (Mp).
(ltp) = 1 = Mp
(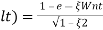 Sin(Wat + φ )
Sin(Wat + φ )
(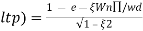 Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2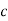
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
(4). Settling Time (ts) :
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Key takeaway
Rise Time tr = 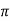 -ø/wd
-ø/wd
Peak Time tp = n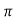 /wd for n=1
/wd for n=1
tp = 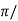 wd
wd
Peak Overshoot Value
Mp% = e-∏ξ / √1 –ξ2
Settling Time
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Examples
Q.1. The open loop transfer function of a system with unity feedback gain G(S) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Soln: Finding closed loop transfer function,
C( S ) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Settling time (v) Peak overshoot.
Sol: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by
G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Soln: C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
Forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Soln:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
Stability of system from pole locations
A) Real and negative G(s)= 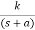
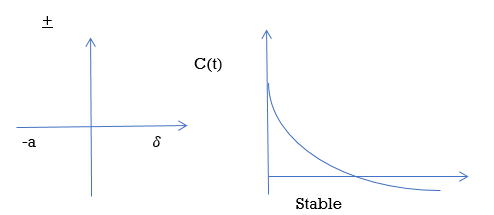
Fig 18 Output for G(s)= 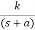
B) Poles on right half of S- plane
G(s) = 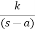
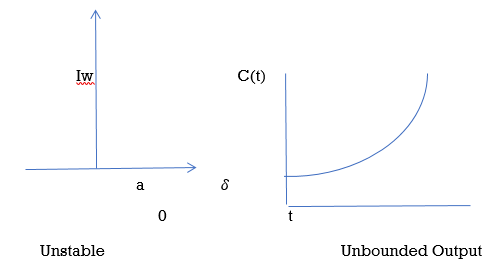
Fig 19 Input and Output for G(s) = 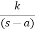
(C)Poles at origin
G(s)=
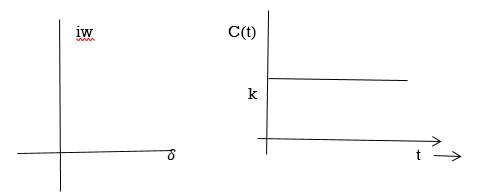
Marginally stable
Fig 20 Input and output for G(s)=
4) Complex poles on left half of S-plane
S1, S2= -α ± iw
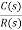 =
= 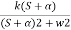
C(t) = k e- αt Cos wt
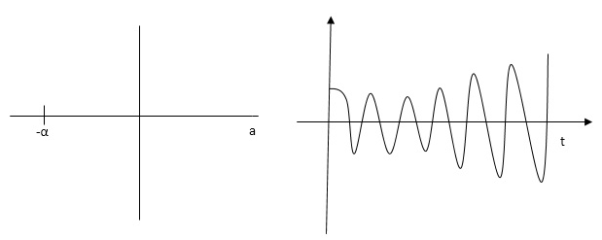
Fig 21 Input and output of C(t) = k e- αt Cos wt
At t - ∞ C(t) – 0 so, system stable
5) Complex poles on right half of S-plane
S1, S2 = α ± iw.
C(t) = k eαt COSwt
 C(t) increases exponentially with t ∞
C(t) increases exponentially with t ∞
So, unstable.
6) Poles on iw axis:
S1, S2 = ± iw.
C(t) = k COS wt.
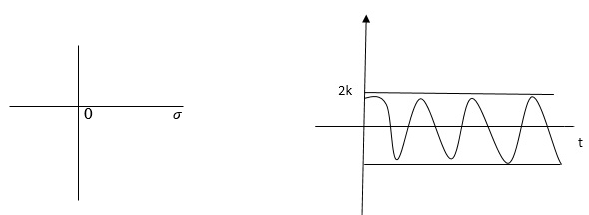
Fig 22 Output of C(t) = k COS wt
The system is marginally stable than sustained so illations.
Key takeaway
Consider a system with characteristic equation
aoSm + a1 Sm-1 ……………..am=0.
1) All the coefficients of above equation should have same sign.
2) There should be no missing term.
The above two condition are necessary but not sufficient condition for stability
Routh Hurwitz stability criterion
It states that the system is stable if and only if all the elements is the first column have the same algebraic sign. If all elements are not of the same sign then the number of sign changes of elements in first column equals the number of roots of the characteristic equation in the right half of S-plane.
Consider the following characteristic equation:
a0 Sn + a1 Sn-1 ………….an = 0 where a0,a1,,,,,,,,,,,,,,,,,,,,an have same sign and are non-zero.
Step1 Arrange coefficients in rows
Row1 ao a2 a4
Row2 a1 a3 a5
Step2 Find third row from above two rows
Row1 a0 a2 a4
Row2 a1 a3 a5
Row3 a1 a3 a5
a1 = 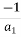
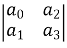 =
= 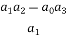
a3 = 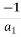
 =
= 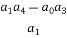
Continue the same procedure to find new rows.
Q1) for the given polynomials below determine the stability of the system
S4+2S3+3S2+4S+5=0
1) Arranging Coefficient in Rows.
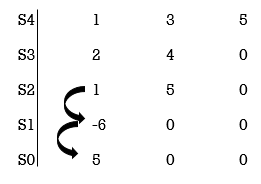
For row S2 first term
S2 = 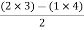 = 1
= 1
For row S2 Second term
S2 = 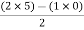 = 5
= 5
For row S1:
S1 = 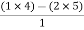 = -6
= -6
For row S0
S0 = 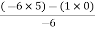 = 5
= 5
As there are two sign change in the first column, So there are two roots or right half of S-plane making system unstable.
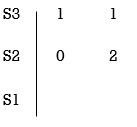
Q2. Using Routh criterion determine the stability of the system with characteristic equation S4+8S3+18S2+16S+S = 0
Sol: Arrange in rows.
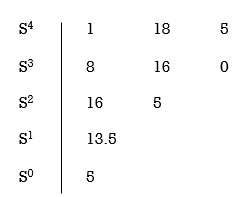
For row S2 first element
S1 = 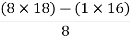 = 16
= 16
Second terms = 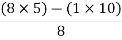 = 5
= 5
For S1
First element = 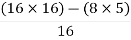 = 13.5
= 13.5
For S0
First element = 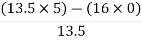 = 5
= 5
As there is no sign change for first column so all roots are is left half of S-plane and hence system is stable.
Special Cases of Routh Hurwitz Criterions
- When first element of any row is zero.
In this case the zero is replaced by a very small positive number E and rest of the array is evaluated.
Eg.(1) Consider the following equation
S3+S+2 = 0
Replacing 0 by E
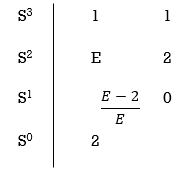
Now when E  0, values in column 1 becomes
0, values in column 1 becomes
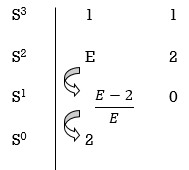
Two sign changes hence two roots on right side of S-plans
II) When any one row is having all its terms zero.
When array one row of Routh Hurwitz table is zero, it shown that the X is attests one pair of roots which lies radially opposite to each other in this case the array can be completed by auxiliary polynomial. It is the polynomial row first above row zero.
Consider following example
S3 + 5S2 + 6S + 30
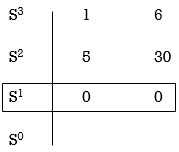
For forming auxiliary equation, selecting row first above row hang all terms zero.
A(s) = 5S2 e 30
 = 10s e0.
= 10s e0.
Again forming Routh array
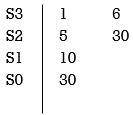
No sign change in column one the roots of Auxiliary equation A(s)=5s2+ 30-0
5s2+30 = 0
S2 α 6= 0
S = ± j 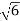
Both lie on imaginary axis so system is marginally stable.
Q3. Determine the stability of the system represent by following characteristic equations using Routh criterion
1) S4 + 3s3 + 8s2 + 4s +3 = 0
2) S4 + 9s3 + 4S2 – 36s -32 = 0
1) S4+3s3+8s2+4s+3=0
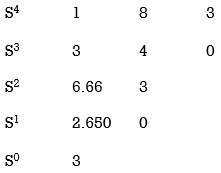
No sign change in first column to no rows on right half of S-plane system stable.
S4+9S3+4S2-36S-32 = 0
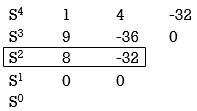
Special case II of Routh Hurwitz criterion forming auxiliary equation
A1 (s) = 8S2 – 32 = 0
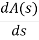 = 16S – 0 =0
= 16S – 0 =0
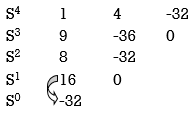
One sign change so, one root lies on right half S-plane hence system is unstable.
Q4. For using feedback open loop transfer function G(s) = 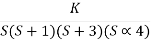
Find range of k for stability
Soln: Findlay characteristics equation.
CE = 1+G (s) H(s) = 0
H(s) =1 using feedback
CE = 1+ G(s)
1+ 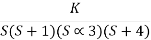 = 0
= 0
S(S+1)(S+3)(S+4)+k = 0
(S2+5)(S2+7Sα12)αK = 0
S4α7S3α1252+S3α7S2α125αK = 0
S4+8S3α19S2+125+k = 0
By Routh Hurwitz Criterion
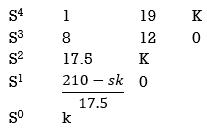
For system to be stable the range of K is 0< K < 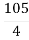 .
.
Q5. The characteristic equation for certain feedback control system is given S4 +4S3+ 12S2+36S+K. Find range of K for system to be stable.
Sol:

S4+4S3α12S2+36SαK = 0
For stability K>0
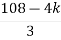 > 0
> 0
K < 27
Range of K will be 0 < K < 27
Relative Stability:
Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.
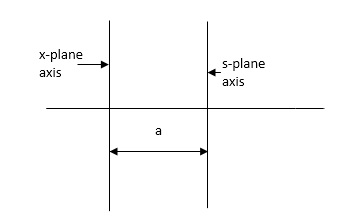
Fig 23 Location of Pole for relative stability
The above fig 10 shows the characteristic equation is modified by shifting the origin of S-plane to S1= -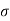 .
.
S = Z-S1
After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane
Q6. Check if all roots of equation
S3+6S2+25S+38 = 0, have real poll more negative than -1.
Soln:

No sign change in first column, hence all roots are in left half of S-plane.
Replacing S = Z-1. In above equation
(Z-1)3+6(Z-1)2+25(Z-1)+38 = 0
Z3+ Z23+16Z+18=0
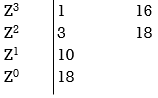
No sign change in first column roots lie on left half of Z-plane hence all roots of original equation in S-domain lie to left half 0f S = -1
Key takeaway
Special Cases of Routh Hurwitz Criterions
- When first element of any row is zero.
In this case the zero is replaced by a very small positive number E and rest of the array is evaluated.
II) When any one row is having all its terms zero.
When array one row of Routh Hurwitz table is zero, it shown that the X is attests one pair of roots which lies radially opposite to each other in this case the array can be completed by auxiliary polynomial. It is the polynomial row first above row zero.
Relative Stability:
Routh stability criterion deals about absolute stability of any closed loop system. For relative stability we need to shift the S-plane and the apply the Routh criterion.
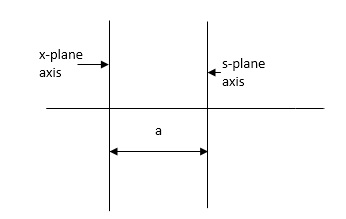
Fig 24 Location of Pole for relative stability
The above fig 10 shows the characteristic equation is modified by shifting the origin of S-plane to S1= -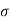 .
.
S = Z-S1
After substituting new valve of S =(Z-S1) applying Routh stability criterion, the number of sign changes in first column is the number of roots on right half of S-plane
The root locus is a graphical produce for determining the stability of a control system which is determined by the location of the poles. The poles are nothing but the roots of the characteristic equation.
Features of Root Locus
- It is symmetrical to the real axis.
- Number of branches of root locus is equal to number of max (poles or zero).
- Starting point (k=0) End point(k—>∞)
(open loop poles) (open loop zeros)
4. A point on the real axis lies on the root locus if number of open loop poles or zero to the right side of that point is odd in number.
5. Value of K anywhere on the root locus is given as
K = 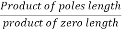
6. I)If poles > zeros then (Þ-z) branches will terminate at ∞ (where k=∞)
II)If Z > P, then (Z-P) branches will start from ∞ (K = 0)
7. When P>Z, (P-Z) branches will terminate at ∞ (open loop zeros). But by which path. So the path is shown by asymptotes and this asymptotes is given by
Asymptote = 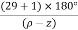 q = o,1,2……(P-Z-1)
q = o,1,2……(P-Z-1)
8. There asymptotes intersect the real axis at a single point and this point is known as centroid.
Centroid = 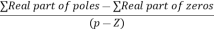
9. Break away and break in point when root locus lie between two poles its called break in point.
Centroid and Breakaway points are not same
Differentials the characteristic equation and equate to zero 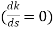
10. Angle of arrival and angle of departure this print is used when the roots are complex.
Angle of departure - for complex poles
Angle of arrival – for complex zero.
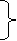 øD =(2q+1) 180° + ø
øD =(2q+1) 180° + ø
øA = (2q+1) 180° - ø ø = ∠Z– ∠P.
11. Intersection of root locus with imaginary axis can be calculated by Routh Hurwitz. By calculating valve of k at intersection point (we can comment about system stability) so by knowing values of k at intersection point (imaginary axis) the valve of s at that point can also be calculated.
Absolutely stable: If the root low (all the branches) lies within the left side of S-plane.
Conditionally Stable: If some part of the root locus lies on the left half and same
Part on the right of S-plane then it is conditionally stable.
Unstable: If the root locus lies completely on right side of S-plane then it is unstable.
The values of S which satisfy both the angle and magnitude conditions are the roots of the characteristic equation.
Angle condition:
LG(S)H(S) = +-1800(2 KH) (K = 1,2,3, --)
If angle is odd multiple of 1800 it satisfies above condition.
Magnitude condition:
| G(S)H(S) = 1 | at any point on root locus. The magnitude condition can be applied only if angle condition is satisfied.
Q1. Sketch the root locus for given open loop transfer function G(S) = 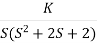 .
.
Soln: 1) G(s) = 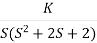
Number of Zeros = 0
Number of polls S = (0, -1+j, -1-j) = (3).
1) Number of Branches = max (P, Z) = max (3, 0) = 3.
2) As there are no zeros in the system so, all branches terminate at infinity.
3) As P>Z, branches terminate at infinity through the path shown by asymptotes
Asymptote = 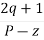 × 180° q = 0, 1, 2………..(p-z-1)
× 180° q = 0, 1, 2………..(p-z-1)
P=3, Z=0.
q= 0, 1, 2.
For q=0
Asymptote = 1/3 × 180° = 60°
For q=1
Asymptote =  × 180°
× 180°
= 180°
For q=2
Asymptote =  × 180° = 300°
× 180° = 300°
Asymptotes = 60°,180°,300°.
4) Asymptote intersects real axis at centroid
Centroid =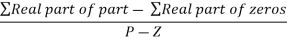
= 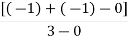
Centroid = -0.66
5) As poles are complex so angle of departure
øD = (2q+1)×180°+ø
ø = ∠Z –∠P.
Calculating ø for S=0
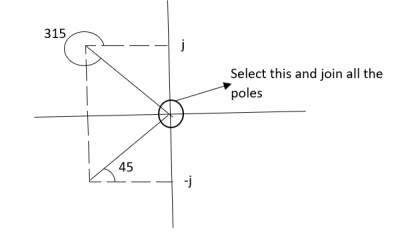
Join all the other poles with S=0
ø = ∠Z –∠P.
= 0-(315°+45°)
= -360°
ØD = (2q + 1)180 + ø.
= 180° - 360°
ØD = -180° (for q=0)
= 180° (for q=1)
=540° (for q=2)
Calculation ØD for pole at (-1+j)
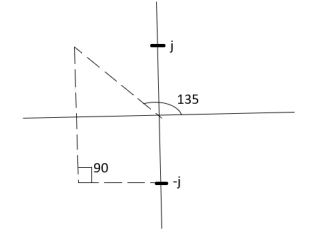
ø = ∠Z –∠P.
= 0 –(135°+90°)
= -225°
ØD = (2q+1) 180°+ø.
= 180-225°
= -45°
ØD = -45° (for q = 0)
= 315° (for q = 1)
= 675° (for q =2)
6) The crossing point on imaginary axis can be calculated by Routh Hurwitz the characteristic equation is.
1+G(s) H (s) = 0
1+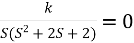
S (S2+2s+2)+k = 0
S3+2s2+2s+K = 0
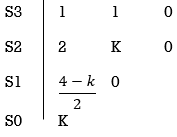
For stability 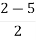 > 0. And K > 0.
> 0. And K > 0.
0<K<2.
So, when K=2 root locus crosses imaginary axis
S3 + 2S2 + 2S + 2 =0
For k
Sn-1 = 0 n: no. Of intersection
S2-1 = 0 at imaginary axis
S1 = 0
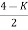 = 0
= 0
K<4
For Sn = 0 for valve of S at that K
S2 = 0
2S2 + K = 0
2S2 + 2 = 0
2(S2 +1) = 0
32 = -2
S = ± j 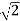
The root locus plot is shown in figure.
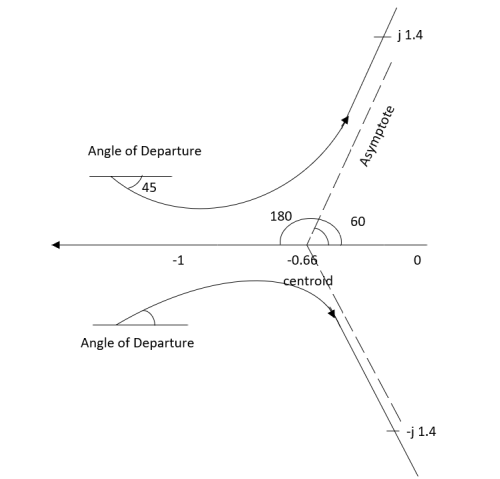
Fig 25 Root Locus for G(S) = 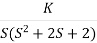
Q2. Sketch the root locus plot for the following open loop transfer function
G(s) = 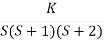
- Number of zero = 0, number of poles = 3
- As P>Z, branches will terminate at infinity
- There are no zeros so all branches will terminate at infinity.
- The path for the branches is shown by asymptote
Asymptote = 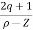 ×180°. q=0,1,………p-z-1
×180°. q=0,1,………p-z-1
P=3, Z=0
q= 0,1,2.
For q = 0
Asymptote =  × 180° = 60.
× 180° = 60.
For q=1
Asymptote =  × 180° = 180°
× 180° = 180°
For q=2
Asymptote =  × 180° = 300°
× 180° = 300°
5. Asymptote intersect real axis at centroid
Centroid = 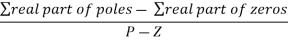
= 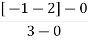 = -1
= -1
6. As root locus lies between poles S= 0, and S= -1
So, calculating breakaway point.
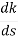 = 0
= 0
The characteristic equation is
1+ G(s) H (s) = 0.
1+ 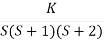 = 0
= 0
K = -(S3+3S2+2s)
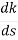 = 3S2+6s+2 = 0
= 3S2+6s+2 = 0
3s2+6s+2 = 0
S = -0.423, -1.577.
So, breakaway point is at S=-0.423
Because root locus is between S= 0 and S= -1
7. The intersection of root locus with imaginary axis is given by Routh criterion.
Characteristics equation is
S3+3S3+2s+K = 0
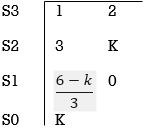
For k
Sn-1= 0 n: no. Of intersection with imaginary axis
n=2
S1 = 0
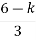 = 0
= 0
K < 6 Valve of S at the above valve of K
Sn = 0
S2 = 0
3S2 + K =0
3S2 +6 = 0
S2 + 2 = 0
S = ± 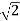 j
j
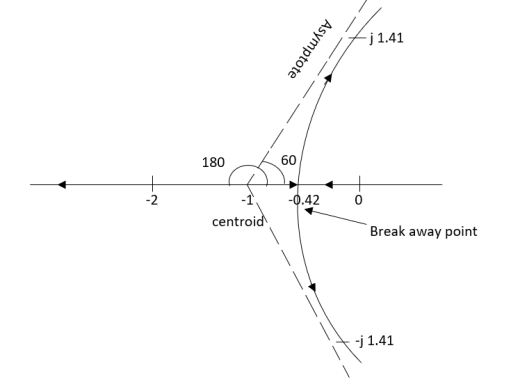
Fig 26 Root Locus for G(s) = 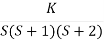
The root locus plot is shown in figure.
Q3. Plot the root locus for the given open loop transfer function
G(s) = 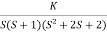
- Number of zeros = 0 number of poles = 4
P = (S=0, -1, -1+j, -1-j) = 4
2. As P>Z all the branches will terminated at infinity.
3. As no zeros so all branches terminate at infinity.
4. The path for branches is shown by asymptote.
Asymptote = 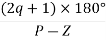 q = 0,1,…..(Þ-z-1)
q = 0,1,…..(Þ-z-1)
q=0,1,2,3. (P-Z = 4-0)
For q=0
Asymptote =  ×180° =45°
×180° =45°
For q=1
Asymptote =  ×180° =135°
×180° =135°
For q=2
Asymptote =  ×180° =225°
×180° =225°
For q=3
Asymptote =  ×180° =315°
×180° =315°
5. Asymptote intersects real axis at unmarried
Centroid = 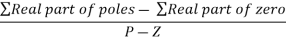
Centroid = 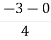 =
= 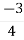 = -0.75
= -0.75
6) As poles are complex so angle of departure is
ØD = (2q+1) ×180 + ø ø = ∠Z –∠P.
A) Calculating Ø for S=0
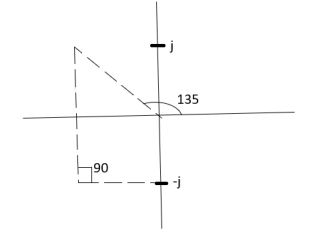
ø = ∠Z –∠P.
= 0 –[315° + 45°]
Ø = -360°
For q = 0
ØD = (2q+1) 180° + Ø
= 180 - 360°
ØD = -180°
b) Calculating Ø for S=-1+j
ø = ∠Z –∠P.
= 0-[135° + 90° + 90°]
Ø = -315°
For q=0
ØD= (2q+1) 180° +Ø
= 180° -315°
ØD = -135°
ØD for S=1+j will be ØD = 45°
7) As the root locus lie between S=0 and S=-1
So, the breakaway point is calculated
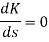
1+ G(s)H(s) = 0
1+ 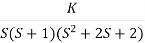 = 0
= 0
(S2+S)(S2 +2S+2) + K =0
K = -[S4+S3+2s3+2s2+2s2+2s]
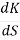 = 4S3+9S2+8S+2=0
= 4S3+9S2+8S+2=0
S = -0.39, -0.93, -0.93.
The breakaway point is at S = -0.39 as root locus exists between S= 0 and S=-1
8) Intersection of root locus with imaginary axis is given by Routh Hurwitz
I + G(s) H(s) = 0
K+S4+3S3+4S2+2S=0

For system to be stable
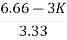 >0
>0
6.66>3K
0<K<2.22.
For K = 2.22
3.3352+K =0
3.3352 + 2.22 = 0
S2 = -0.66
S = ± j 0.816.
The root locus plot is shown in figure 27.
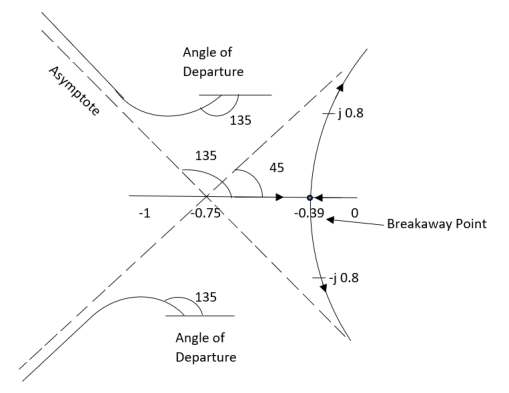
Fig 27 Root Locus for G(s) = 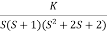
Q4. Plot the root locus for open loop system
G(s) = 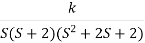
1) Number of zero = 0 number of poles = 4 located at S=0, -2, -1+j, -1-j.
2) As no zeros are present so all branches terminated at infinity.
3) As P>Z, the path for branches is shown by asymptote
Asymptote = 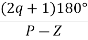
q = 0,1,2……p-z-1
For q = 0
Asymptote = 45°
q=1
Asymptote = 135°
q=2
Asymptote = 225°
q=3
Asymptote = 315°
4) Asymptote intersects real axis at centroid.
Centroid = 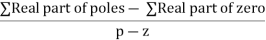
= 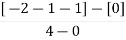
Centroid = -1.
5) As poles are complex so angle of departure is
ØD=(2q+1)180° + Ø
ø = ∠Z –∠P
= 0-[135°+45°+90°]
= 180°- 270°
ØD = -90°
6) As root locus lies between two poles so calculating point. The characteristic equation is
1+ G(s)H(s) = 0
1+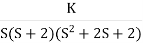 = 0.
= 0.
K = -[S4+2S3+2S2+2S3+4S2+4S]
K = -[S4+4S3+6S2+4S]
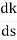 = 0
= 0
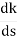 = 4s3+12s2+12s+4=0
= 4s3+12s2+12s+4=0
S = -1
So, breakaway point is at S = -1
7) Intersection of root locus with imaginary axis is given by Routh Hurwitz.
S4+4S3+6S2+4s+K = 0
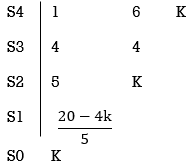
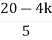 ≤ 0
≤ 0
K≤5.
For K=5 valve of S will be.
5S2+K = 0
5S2+5 = 0
S2 +1 = 0
S2 = -1
S = ±j.
The root locus is shown in figure 28.
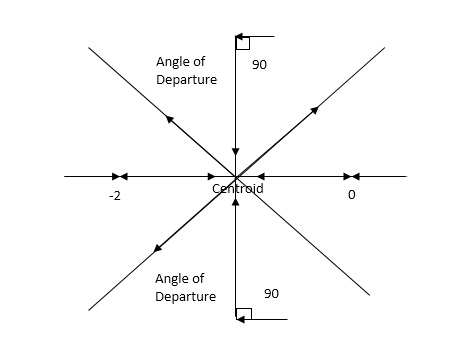
Fig 28 Root Locus For G(s) = 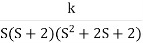
Q5. Plot the root locus for open loop transfer function G(s) = 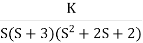
- Number of zeros = 0. Number of poles = 4 located at S=0, -3, -1+j, -1-j.
- As no. Zero so all branches terminate at infinity.
- The asymptote shows the both to the branches terminating at infinity.
Asymptote = 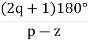 q=0,1,….(p-z).
q=0,1,….(p-z).
For q = 0
Asymptote = 45
For q = 1
Asymptote = 135
For q = 2
Asymptote = 225
For q = 3
Asymptote = 315
(4). The asymptote intersects real axis at centroid.
Centroid = ∑Real part of poles - ∑Real part of zero / P – Z
= [-3-1-1] – 0 / 4 – 0
Centroid = -1.25
(5). As poles are complex so angle of departure
φD = (29 + 1)180 + φ
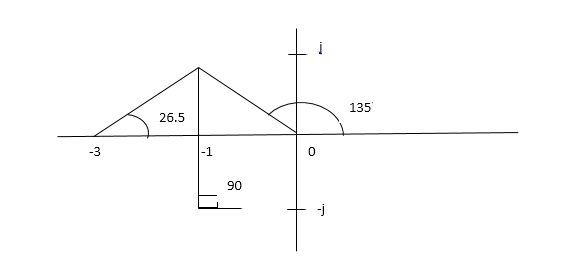
ø = ∠Z –∠P.
= 0 – [ 135 + 26.5 + 90]
= -251.56
For q = 0
φD = (29 + 1)180 + φ
= 180 – 215.5
φD = - 71.56
(6). Break away point dk / ds = 0 is at S = -2.28.
(7). The intersection of root locus on imaginary axis is given by Routh Hurwitz.
1 + G(S)H(S) = 0
K + S4 + 3S3 + 2S3 + 6S2 + 2S2 + 6S = 0
S4 1 8 K
S3 5 6
S2 34/5 K
S1 40.8 – 5K/6.8
K ≤ 8.16
For K = 8.16 value of S will be
6.8 S2 + K = 0
6.8 S2 + 8.16 = 0
S2 = - 1.2
S = ± j1.09
The plot is shown in figure.
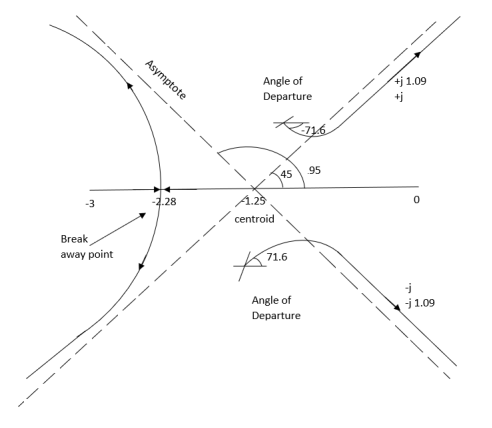
Fig 29 Root Locus for G(s) = 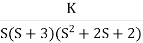
Q.6. Sketch the root locus for open loop transfer function.
G(S) = K(S + 6)/S(S + 4)
- Number of zeros = 1(S = -6)
Number of poles = 2(S = 0, -4)
2. As P > Z one branch will terminate at infinity and the other at S = -6.
3. For Break away and breaking point
1 + G(S)H(S) = 0
1 + K(S + 6)/S(S + 4) = 0
Dk/ds = 0
S2 + 12S + 24 = 0
S = -9.5, -2.5
Breakaway point is at -2.5 and Break in point is at -9.5.
4. Root locus will be in the form of a circle. So finding the centre and radius. Let S = + jw.
G( + jw) = K( + jw + 6)/( + jw)( + jw + 4 ) = +- π
Tan-1 w/ + 6 - tan-1 w/ – tan-1 w / + 4 = - π
Taking tan of both sides.
w/ + w/ + 4 / 1 – w/ w/ + 4 = tan π + w / + 6 / 1 - tan π w/ + 6
w/ + w/ + 4 = w/ + 6[ 1 – w2 / ( + 4) ]
(2 + 4)( + 6) = (2 + 4 – w2)
2 2 + 12 + 4 + 24 = 2 + 4 – w2
22 + 12 + 24 = 2 – w2
2 + 12 – w2 + 24 = 0
Adding 36 on both sides
( + 6)2 + (w + 0)2 = 12
The above equation shows circle with radius 3.46 and center (-6, 0) the plot is shown in figure 30.
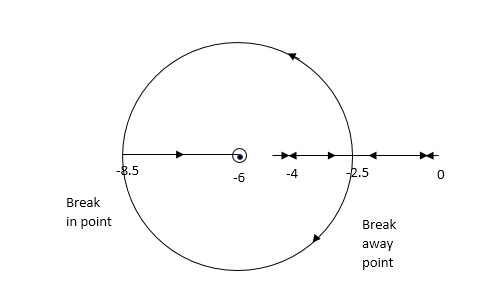
Fig 30 Root locus for G(S) = K (S + 6)/S (S + 4)
References:
[1] I. J. Nagrath and M. Gopal, “Control Systems Engineering”, New Age International,
2009.
[2] K. Ogata, “Modern Control Engineering”, Prentice Hall, 1991
[3] M. Gopal, “Control Systems: Principles and Design”, McGraw Hill Education, 1997.
[4] B. C. Kuo, “Automatic Control System”, Prentice Hall, 1995.