Unit - 3
Relationship between time and frequency response
The calculation of system parameters for higher order systems is difficult in time domain analysis. This can be overcome by frequency domain analysis. As the frequency response of a linear time invariant system is independent of amplitude and phase of the input test signal. The effect of noise and parameter variation in frequency domain can be easily computed.
In frequency response can be determine by calculating the phase and amplitude oof the given system transfer function. If a sinusoidal signal XG(j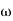 )sin
)sin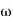 t then its amplitude will be
t then its amplitude will be
C(t) = XG(j )sin
)sin t= X|G(j
t= X|G(j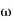 )|
)|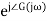 sin
sin t
t
Magnitude = |G(j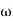 )|
)|
Phase = 
In polar form = |G(j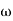 )|
)|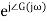
The transfer function of second order system is shown as
C(S)/R(S) = W2n / S2 + 2ξWnS + W2n - - (1)
ξ = Ramping factor
Wn = Undamped natural frequency for frequency response let S = jw
C(jw) / R(jw) = W2n / (jw)2 + 2 ξWn(jw) + W2n
Let U = W/Wn above equation becomes
T(jw) = W2n / 1 – U2 + j2 ξU
So,
| T(jw) | = M = 1/√(1 – u2)2 + (2ξU)2 - - (2)
T(jw) = φ = -tan-1[ 2ξu/(1-u2)] - - (3)
For sinusoidal input the output response for the system is given by
C(t) = 1/√(1-u2)2 + (2ξu)2Sin[wt - tan-1 2ξu/1-u2] - - (4)
The frequency where M has the peak value is known as Resonant frequency Wn. This frequency is given as (from eqn (2)).
DM/du|u=ur = Wr = Wn√(1-2ξ2) - - (5)
From equation(2) the maximum value of magnitude is known as Resonant peak.
Mr = 1/2ξ√1-ξ2 - - (6)
The phase angle at resonant frequency is given as
Φr = - tan-1 [√1-2ξ2/ ξ] - - (7)
As we already know for step response of second order system the value of damped frequency and peak overshoot are given as
Wd = Wn√1-ξ2 - - (8)
Mp = e- πξ2|√1-ξ2 - - (9)
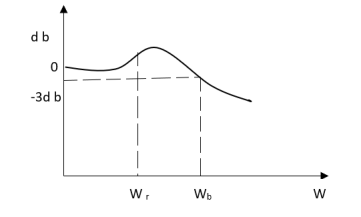

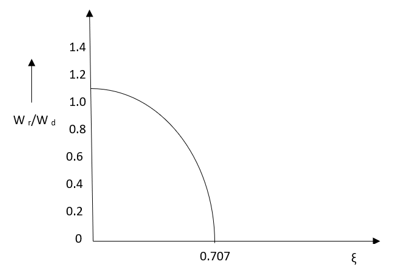
Fig 1 Frequency Domain Specification
The comparison of Mr and Mp is shown in figure. The two performance indices are correlated as both are functions of the damping factor ξ only. When subjected to step input the system with given value of Mr of its frequency response will exhibit a corresponding value of Mp.
Similarly the correlation of Wr and Wd is shown in figure for the given input step response [ from eqn(5) & eqn(8) ]
Wr/Wd = √(1- 2ξ2)/(1-ξ2)
Mp = Peak overshoot of step response
Mr = Resonant Peak of frequency response
Wr = Resonant frequency of Frequency response
Wd = Damping frequency of oscillation of step response.
From fig(1) it is clear that for ξ> 1/2, value of Mr does not exists.
Key takeaways:
i) Mr and Mp are correlated as both are functions of the damping factor ξ only
Ii) When subjected to step input the system with given value of Mr of its frequency response will exhibit a corresponding value of Mp.
It gives the frequency response of the system. If the transfer function is given, then from the plot number of poles and zeros can be calculated.
Polar plot of some standard functions:
# TYPE ‘O’
Ex: 1T(S) = 1/S + 1
(1). For polar plot substitute S=jw.
TF = 1/1 + jw
(2). Magnitude M = 1 + 0j / 1 + jw = 1/√1 + w2
(3). Phase φ = tan-1(0)/ tan-1w = - tan-1w
W M φ
0 1 00
1 0.707 -450
∞ 0 -900
The plot is shown in fig. 2(a)
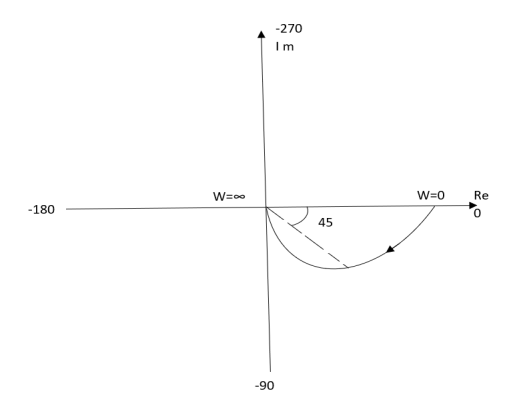
Fig 2(a) Polar Plot T(S) = 1/S + 1
Ex.2>. T(S) = 1/(S+1)(S+2)
(1). S = jw
TF = 1/(1+jw)(2+jw)
(2). M = 1/(1+jw)(2+jw) = 1/-w2 + 3jw + 2
M = 1/√1 + w2√4 + w2
(3). Φ = - tan-1 w - tan-1(w/2)
W M Φ
0 0.5 00
1 0.316 -71.560
2 0.158 -108.430
∞ 0 -1800
The plot is shown in fig2(b)
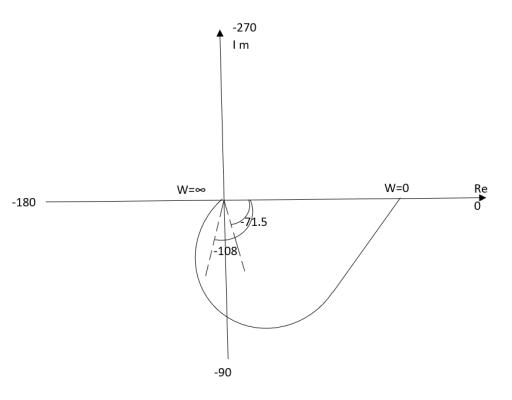
Fig2(b) Polar Plot T(S) = 1/(S+1)(S+2)
Intersection of polar plot with imaginary axis will be when real part of Transfer function = 0
M = 1/(jw + 1)(jw + 2)
= 1/-w2 + j3w + 2
TYPE ‘1’
Ex.1 T(S) = 1/S
(1). S = jw
(2). M = 1/W
(3). Φ = -tan-1(W/O) = -900
W M φ
0 ∞ -900
1 1 -900
2 0.5 -900
∞ 0 -900
The plot is shown in fig.3(a)
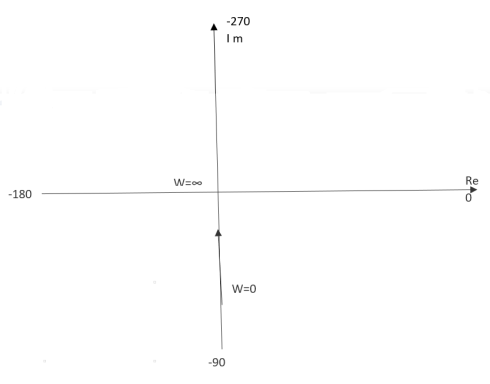
Fig 3(a) Polar Plot T(S) = 1/S
Ex.2 T(S) = 1/S2
(1). S = jw
(2). M = 1/w2
(3). Φ = -tan-1(W/O)-tan-1(W/O) = -1800
W M Φ
0 ∞ -1800
1 1 -1800
2 0.25 -1800
∞ 0 -1800
The plot is shown in fig.3(b)

Fig 3(b) Polar Plot T(S) = 1/S2
Key takeaways:
- For Polar Plot starting point depends upon type of system
- The terminating phase depends on order of the system.
TYPE 1 ORDER 2
Ex.1 T(S) = 1/S(S+1)
(1). M = 1/W√1+w2
(2). Φ = -900 - tan -1(W/T)
W M φ
0 ∞ -900
1 0.707 -1350
2 0.45 -153.40
∞ 0 -1800
The plot is shown in fig.4(a)
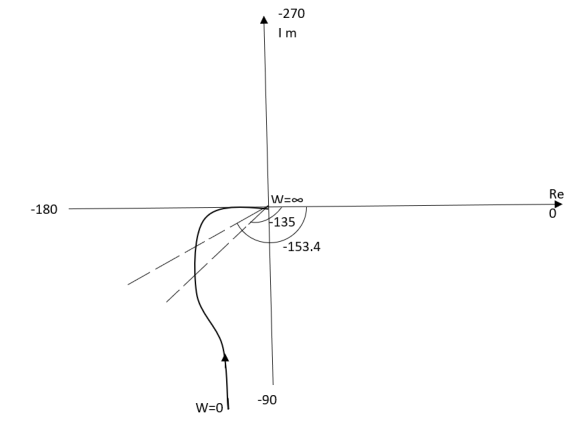
Fig 4(a) Polar Plot T(S) = 1/S(S+1)
Ex.2TYPE 2 ORDER 3
T(s) = 1/S2(S+1)
(1). M = 1/w2√1+jw
(2). Φ = -1800 – tan-1W/T
The plot is shown in fig.4(b)
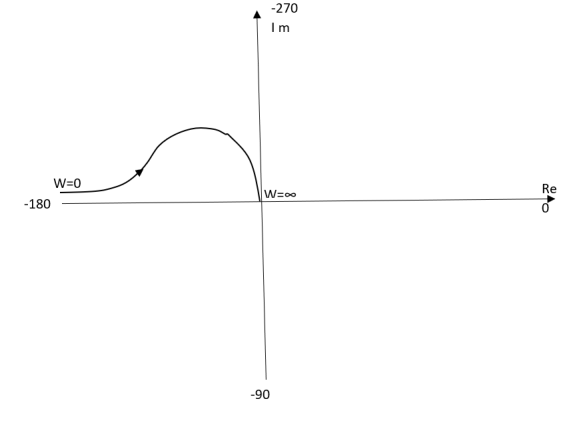
Fig 4(b) Polar Plot T(s) = 1/S2(S+1)
In polar plot any point gives the magnitude phase of the transfer function in bode we split magnitude and  plot.
plot.
Advantages
- By looking at bode plot we can write the transfer function of system
Q. G(S) = 
1. Substitute S = j
G(j ) =
) = 
M = 
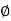 = tan-1
= tan-1 = -900
= -900
Magnitude varies with ‘w’ but phase is constant.
MdB = +20 log10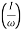
MdB = -20 log10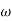
Decade frequency:-
W present = 10 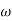 past
past
Then 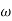 present is called decade frequency of
present is called decade frequency of 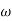 past
past
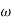 2 = 10
2 = 10 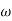 1
1
 2 is decade frequency of
2 is decade frequency of  1
1
 MdB
MdB
0.01 40
0.1 20
1 0 (shows pole at origin)
0 -20
10 -40
100 -60
Slope = (20db/decade)
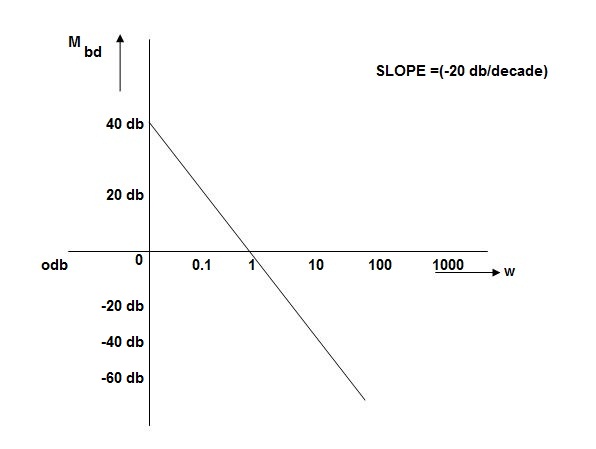
Fig 5 MAGNITUDE PLOT
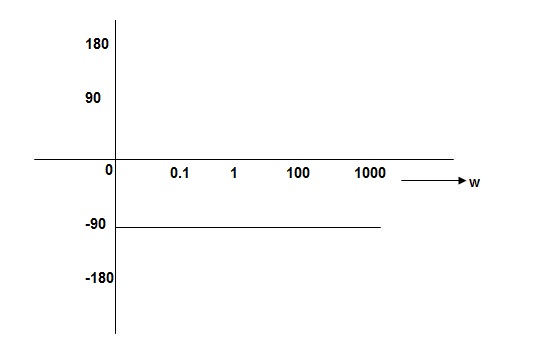
Fig 6 PHASE PLOT
Que.G(S) = 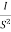
Sol: G(j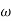 ) =
) = 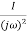
M = 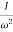 ;
; 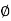 = -1800 (-20tan-1
= -1800 (-20tan-1 )
)
MdB = +20 log 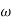 -2
-2
MdB = -40 log10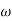
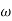 MdB
MdB
0.01 80
0.1 40
1 0 (pole at origin)
10 -40
100 -80
Slope = 40dbdecade
Que. G(S) = S
Sol: M= W
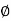 = 900
= 900
MdB = 20 log10
 MdB
MdB
0.01 -40
0.1 -20
1 0
10 20
100 90
1000 60
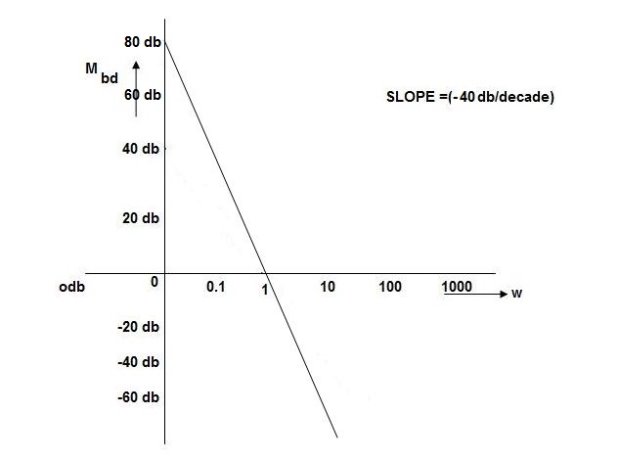
Fig 7 Bode Plot G(S) = S
Que. G(S) = S2
Sol: M=  2
2
MdB = 20 log10 2 == 40 log10
2 == 40 log10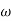
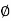 = 1800
= 1800
W MdB
0.01 -80
0.1 -40
1 0
10 40
100 80
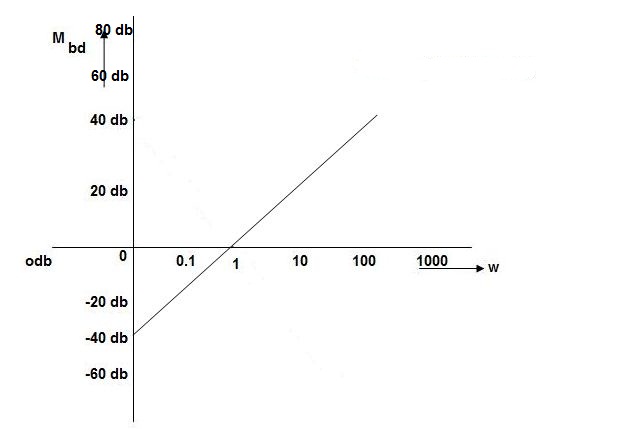
Fig 8 Magnitude Plot G(S) = S2
Que. G(S) = 
Sol: G(j ) =
) = 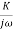
M = 
MdB = 20 log10 K-20 log10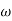
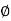 = tan-1(
= tan-1( ) –tan-1(
) –tan-1( )
)
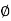 = 0-900 = -900
= 0-900 = -900
K=1 K=10
 MDb MdB
MDb MdB
=-20 log10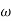 =20 -20 log10
=20 -20 log10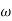
0.01 40 60
0.1 20 40
1 0 20
10 -20 0
100 -40 -20
Fig 9 Bode Plot G(S) = 
Fig 10 All bode plots in one plot
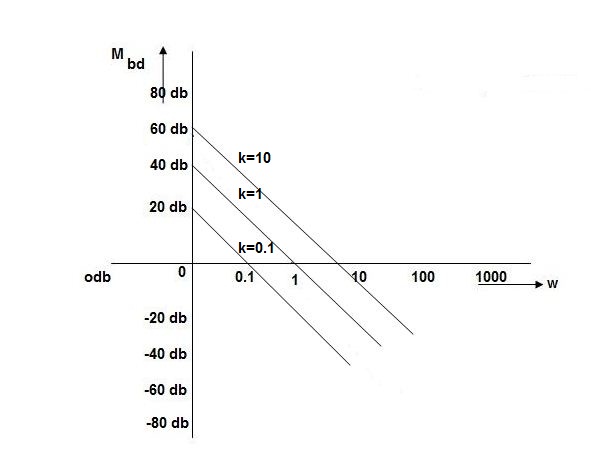
Fig 11 Variation in K shifts magnitude plot by +20db
As we vary K 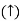 then plot shift by 20 log10K
then plot shift by 20 log10K
i.e adding a d.c. To a.c. Quantity
Approximation of Bode Plot:
If poles and zeros are not located at origin
G(S) = 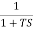
TF = 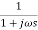
M = 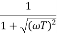
MdB = -20 log10 (
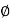 = -tan-1
= -tan-1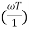
Approximation: 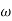 T >> 1. So, we can neglect 1.
T >> 1. So, we can neglect 1.
MdB = -20 log10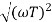
MdB = -20 log10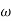 T . ;
T . ; 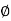 = -tan-1(
= -tan-1(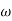 T)
T)
Approximation: 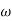 T << 1. So, we can neglect
T << 1. So, we can neglect 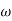 T.
T.
MdB= 0dB,  = 00
= 00
At a point both meet so equal i.e a time will come hence both approx. become equal
-20 log10 T= 0
T= 0
 T= 1
T= 1
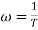 corner frequency
corner frequency
At this frequency both the cases are equal
MdB = -20 log10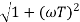
Now for 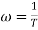
MdB = -20 log10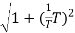
= -20 log10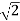
= -10 log102
MdB = 10

Fig 12 Approximation in bode plot
When we increase the value of 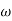 in app 2 and decrease the
in app 2 and decrease the 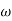 of app 1 so a RT comes when both cases are equal and hence for that value of
of app 1 so a RT comes when both cases are equal and hence for that value of 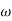 where both app are equal gives max. Error we found above and is equal to 3dB
where both app are equal gives max. Error we found above and is equal to 3dB
At corner frequency we have max error of -3dB
Que. G(S) = 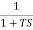
Sol: TF = 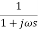
M = 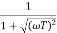
MdB = -20 log10 (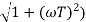 at T=2
at T=2
 MdB
MdB
1 -20 log10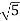
10 -20 log10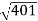
100 -20 log10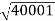
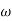 MdB
MdB 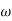 =
= =
= 
0.1 -20 log10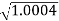 = 1.73
= 1.73 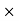 10-3
10-3
0.1 -20 log10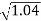 = -0.1703
= -0.1703
0.5 -20 log10 = -3dB
= -3dB
1 -20 log10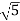 = -6.98
= -6.98
10 -20 log10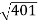 = -26.03
= -26.03
100 -20 log10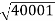 = -46.02
= -46.02
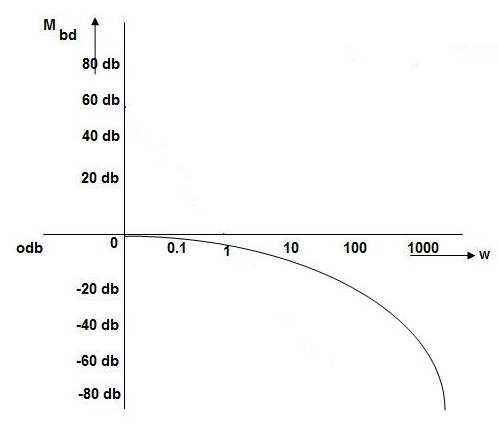
Fig 13 Magnitude Plot with approximation
Without approximation
For second order system
TF = 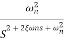
TF = 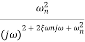
= 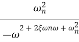
= 
= 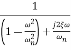
M= 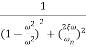
MdB= 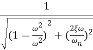
Case 1 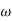 <<
<<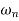
 << 1
<< 1
MdB= 20 log10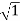 = 0 dB
= 0 dB
Case 2 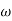 >>
>>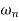
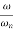 >> 1
>> 1
MdB = -20 log10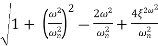
= -20 log10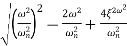
= -20 log10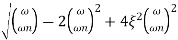
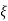 < 1
< 1 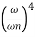 is very large so neglecting other two terms
is very large so neglecting other two terms
MdB = -20 log10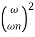
= -40 log10
Case 3 . When case 1 is equal to case 2
-40 log10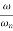 = 0
= 0
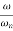 = 1
= 1
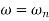
The natural frequency is our corner frequency
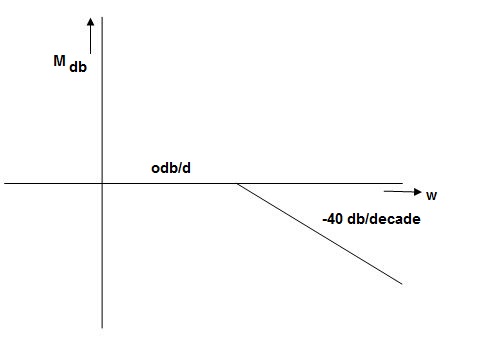
Fig 14 Magnitude Plot
Max error at 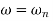 i.e at corner frequency
i.e at corner frequency
MdB = -20 log10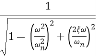
For 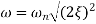
MdB = -20 log10 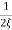
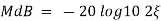 error for
error for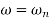
Completely the error depends upon the value of 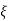 (error at corner frequency)
(error at corner frequency)
The maximum error will be
MdB = -20 log10 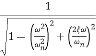
M = -20 log10 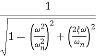
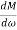 = 0
= 0
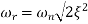
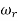 is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
is resonant frequency and at this frequency we are getting the maximum error so the magnitude will be
M = -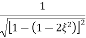 +
+ 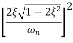
= 
Mr =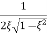
MdB = -20 log10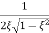
MdB = -20 log10 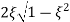
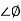 = tan-1
= tan-1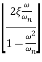

Mr = 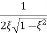
Type of system | Initial slope | Intersection |
0 | 0 dB/decade | Parallel to 0 axis |
1 | -20 dB/decade | =K1 |
2 | -40 dB/decade | =K1/2 |
3 | -60 dB/decade | =K1/3 |
. | . | 1 |
. | . | 1 |
. | . | 1 |
N | -20N dB/decade | =K1/N |
Gain Cross Over Frequency
The frequency at which the bode plot culls the 0db axis is called as Gain Cross Over Frequency.
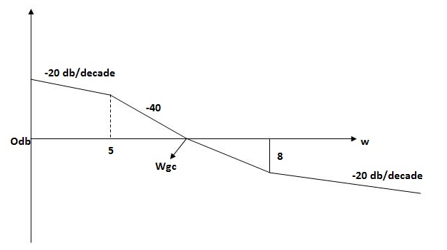
Fig 15 Gain cross over frequency
Phase Cross Over Frequency
The Frequency at which the phase plot culls the -1800 axis.
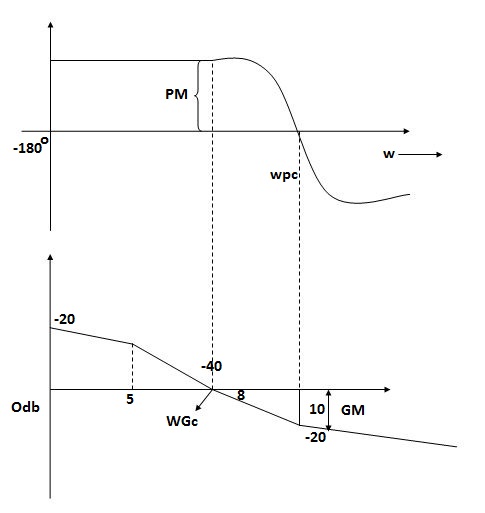
Fig 16 Phase Margin and Gain Margin
GM=MdB= -20 log [ G (jw)]
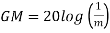 .:
.: 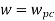
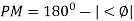 .:
.: 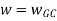
Key takeaways:
i) More the difference b/WPC and WGC core are the stability of system
Ii) If GM is below 0dB axis than take +ve and stable. If GM above 0dB axis, that is take -ve
GM= ODB - 20 log M
Iii) The IM should also lie above -1800 for making the system (i.e. pm=+ve
Iv) For a stable system GM and PM should be -ve
v) GM and PM both should be +ve more the value of GM and PM more the system is stable.
Vi) If Wpc and Wgc are in same line Wpc= Wgc than system is marginally stable as we get GM=0dB.
Vii) When gain cross over frequency is smaller than phase curves over frequency the system is stable and vice versa.
Effect of addition of poles & zeros on bode plot
The effect can be understood by plotting few bode plots as shown below
Q.1 sketch the bode plot for transfer function
G(S) = 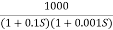
- Replace S = j

G(j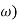 =
= 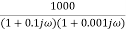
This is type 0 system . So initial slope is 0 dB decade. The starting point is given as
20 log10 K = 20 log10 1000
= 60 dB
Corner frequency  1 =
1 = 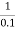 = 10 rad/sec
= 10 rad/sec
 2 =
2 = 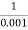 = 1000 rad/sec
= 1000 rad/sec
Slope after  1 will be -20 dB/decadetill second corner frequency i.e
1 will be -20 dB/decadetill second corner frequency i.e  2 after
2 after 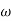 2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2 the slope will be -40 dB/decade (-20+(-20)) as there are poles
2. For phase plot
 = tan-1 0.1
= tan-1 0.1 - tan-1 0.001
- tan-1 0.001 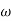
For phase plot
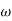
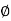
100 -900
200 -9.450
300 -104.80
400 -110.360
500 -115.420
600 -120.00
700 -124.170
800 -127.940
900 -131.350
1000 -134.420
The plot is shown in figure 17
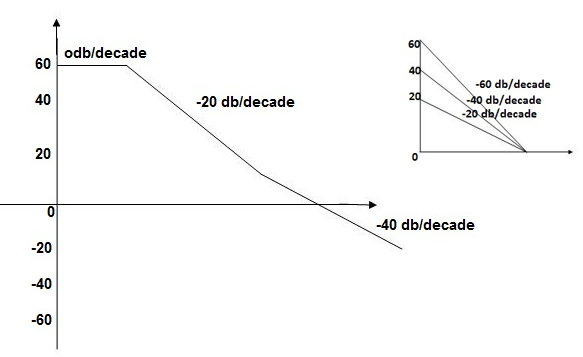
Fig 17 Magnitude Plot for G(S) = 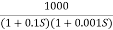
Q.2 For the given transfer function determine
G(S) = 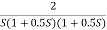
Gain cross over frequency phase cross over frequency phase mergence and gain margin
Initial slope = 1
N = 1, (K)1/N = 2
K = 2
Corner frequency
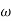 1 =
1 = 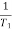 = 2 (slope -20 dB/decade
= 2 (slope -20 dB/decade
 2 =
2 =  = 20 (slope -40 dB/decade
= 20 (slope -40 dB/decade
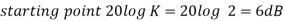
2. phase
 = tan-1
= tan-1 - tan-1 0.5
- tan-1 0.5  - tan-1 0.05
- tan-1 0.05 
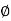 = 900- tan-1 0.5
= 900- tan-1 0.5 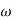 - tan-1 0.05
- tan-1 0.05 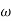
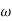
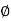
1 -119.430
5 -172.230
10 -195.250
15 -209.270
20 -219.30
25 -226.760
30 -232.490
35 -236.980
40 -240.570
45 -243.490
50 -245.910
Finding 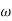 gc (gain cross over frequency
gc (gain cross over frequency
M = 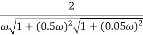
4 = 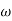 2 (
2 (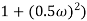 (
(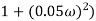
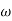 6 (6.25
6 (6.25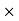 104) + 0.252
104) + 0.252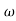 4 +
4 +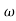 2 = 4
2 = 4
Let 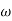 2 = x
2 = x
X3 (6.25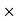 104) + 0.252
104) + 0.252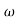 2 + x = 4
2 + x = 4
X1 = 2.46
X2 = -399.9
X3 = -6.50
For x1 = 2.46
 gc = 3.99 rad/sec(from plot )
gc = 3.99 rad/sec(from plot )
For phase margin
PM = 1800 -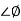
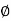 = 900 – tan-1 (0.5×
= 900 – tan-1 (0.5× gc) – tan-1 (0.05 ×
gc) – tan-1 (0.05 × 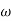 gc)
gc)
= -164.50
PM = 1800 -164.50
= 15.50
For phase cross over frequency (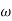 pc)
pc)
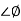 = 900 – tan-1 (0.5
= 900 – tan-1 (0.5 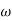 ) – tan-1 (0.05
) – tan-1 (0.05 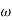 )
)
-1800 = -900 – tan-1 (0.5 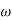 pc) – tan-1 (0.05
pc) – tan-1 (0.05  pc)
pc)
-900 – tan-1 (0.5 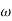 pc) – tan-1 (0.05
pc) – tan-1 (0.05  pc)
pc)
Taking than on both sides
Tan 900 = tan-1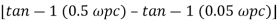
Let tan-1 0.5 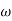 pc = A, tan-1 0.05
pc = A, tan-1 0.05 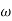 pc = B
pc = B
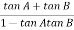 = 00
= 00
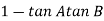 = 0
= 0
1 =0.5 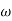 pc 0.05
pc 0.05 pc
pc
 pc = 6.32 rad/sec
pc = 6.32 rad/sec
The plot is shown in figure 18.
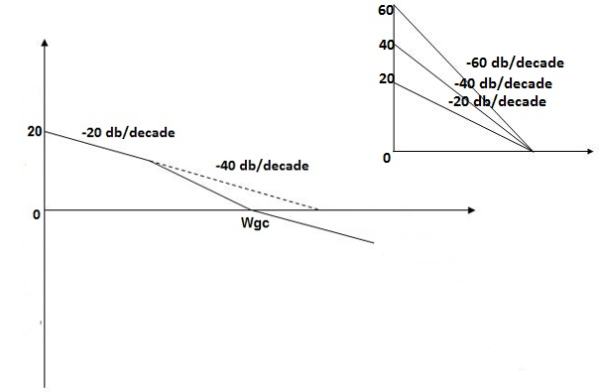
Fig 18 Magnitude Plot G(S) = 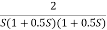
Q3. For the given transfer function
G(S) = 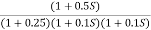
Plot the rode plot find PM and GM
T1 = 0.5 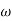 1 =
1 =  = 2 rad/sec
= 2 rad/sec
Zero so, slope (20 dB/decade)
T2 = 0.2 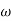 2 =
2 = 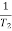 = 5 rad/sec
= 5 rad/sec
Pole, so slope (-20 dB/decade)
T3 = 0.1 = T4 = 0.1
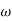 3 =
3 = 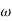 4 = 10 (2 pole) (-40 db/decade)
4 = 10 (2 pole) (-40 db/decade)
- Initial slope 0 dB/decade till
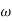 1 = 2 rad/sec
1 = 2 rad/sec - From
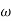 1 to
1 to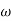 2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade
2 (i.e. 2 rad /sec to 5 rad/sec) slope will be 20 dB/decade - From
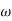 2 to
2 to 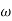 3 the slope will be 0 dB/decade (20 + (-20))
3 the slope will be 0 dB/decade (20 + (-20)) - From
 3,
3,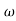 4 the slope will be -40 dB/decade (0-20-20)
4 the slope will be -40 dB/decade (0-20-20)
Phase plot
 = tan-1 0.5
= tan-1 0.5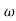 - tan-1 0.2
- tan-1 0.2 - tan-1 0.1
- tan-1 0.1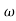 - tan-1 0.1
- tan-1 0.1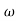

500 -177.30
1000 -178.60
1500 -179.10
2000 -179.40
2500 -179.50
3000 -179.530
3500 -179.60
GM = 00
PM = 61.460
The plot is shown in figure 19
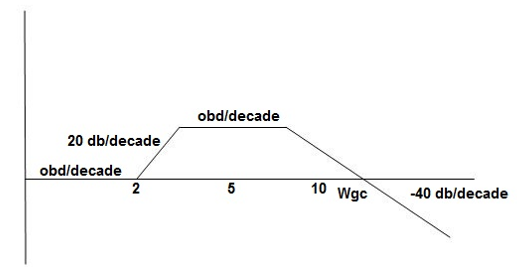
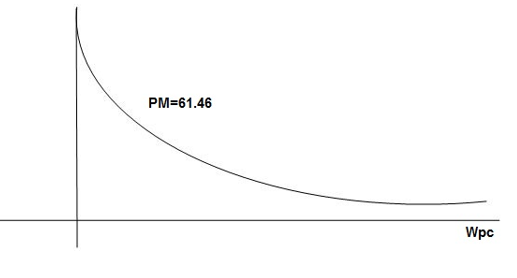
Fig 19 Magnitude and phase Plot for G(S) = 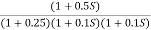
Q 4. For the given transfer function plot the bode plot (magnitude plot) G(S) = 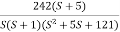
Sol: Given transfer function
G(S) = 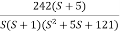
Converting above transfer function to standard from
G(S) = 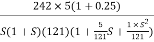
= 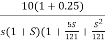
- As type 1 system, so initial slope will be -20 dB/decade
- Final slope will be -60 dB/decade as order of system decides the final slope
- Corner frequency
T1 =  ,
, 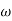 11= 5 (zero)
11= 5 (zero)
T2 = 1, 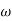 2 = 1 (pole)
2 = 1 (pole)
4. Initial slope will cut zero dB axis at
(K)1/N = 10
i.e. 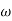 = 10
= 10
5. finding  n and
n and 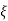
T(S) = 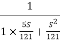
T(S)= 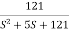
Comparing with standard second order system equation
S2+2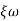 ns +
ns +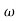 n2
n2
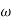 n = 11 rad/sec
n = 11 rad/sec
 n = 5
n = 5
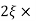 11 = 5
11 = 5
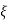 =
= 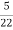 = 0.27
= 0.27
5. Maximum error
M = -20 log 2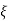
= +6.5 dB
6. As K = 10, so whole plot will shift by 20 log 10 10 = 20 dB
The plot is shown in figure 20
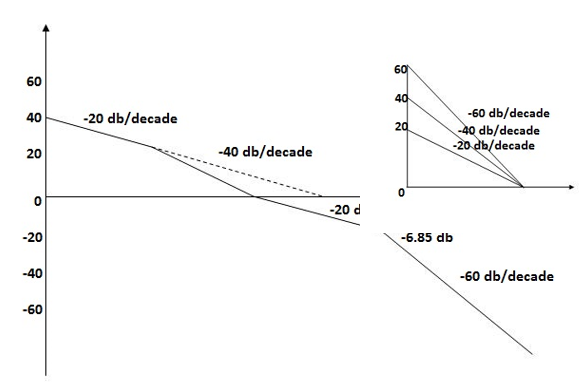
Fig 20 Magnitude Plot for G(S) = 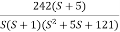
Q5. For the given plot determine the transfer function
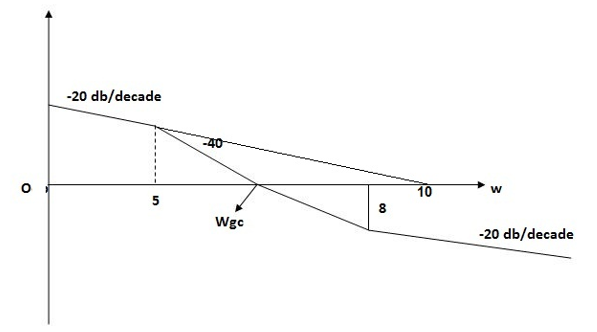
Fig 21 Magnitude Plot
Sol: From figure 21 we can conclude that
- Initial slope = -20 dB/decade so type -1
- Initial slope all 0 dB axis at
 = 10 so
= 10 so
K1/N N = 1
(K)1/N = 10.
3. corner frequency
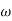 1 =
1 =  = 0.2 rad/sec
= 0.2 rad/sec
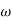 2 =
2 =  = 0.125 rad/sec
= 0.125 rad/sec
3. At 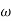 = 5 the slope becomes -40 dB/decade, so there is a pole at
= 5 the slope becomes -40 dB/decade, so there is a pole at 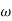 = 5 as
= 5 as
Slope changes from -20 dB/decade to -40 dB/decade
4. At  = 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at
= 8 the slope changes from -40 dB/decade to -20 dB/decade hence is a zero at 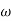 = 8 (-40+(+20) = 20)
= 8 (-40+(+20) = 20)
5. Hence transfer function is T(S) = 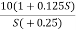
It gives the frequency response as well as comments on the stability and the relative stability of the system.
Nyquist Stability Criteria:
The Nyquist criteria is a semi graphical method that determines stability of CL system investigating the properties of the frequency domain plot (Polar plot), the Nyquist plot of the OLTF G(S) H(S) is represented as L(S)
L(S) = G(S)H(S)
Specially the Nyquist plot of L(S) is a plot drawn by substituting S=jw and varying the value of w as per in polar plot. In polar plot we take one sided frequency response (0 - ∞) in Nyquist plot we will vary the frequency in entire range possible from (-∞ to 0) and (0 to ∞)
Nyquist Criteria also gives:
(1). In addition to providing the absolute stability like other plots, the Nyquist criteria also gives information on the relative stability of a stable system and the degree of instability of an unstable system.
(2). It also gives indications on how the system stability can be improved.
(3). The Nyquist plot of G(S) H(S) is the polar plot of G(S) H(S) drawn with wider range of frequency (-∞ to ∞) and along the Nyquist path.
(4). The Nyquist plot of G(S) H(S) gives information on frequency domain characteristics such as B.W, gain margin and phase margin.
Construction of Nyquist Plot
Encircled: A point or region in a complex function phase i.e. S-plane is said to be encircled by a closed path if it is found inside the path.
Assumption:
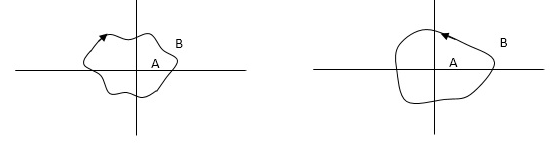
Fig 22 Encirclement
In this example point A is encircled by the closed path Y. Since, A is inside the closed path point B is not encircled by y. It is outside the path. Furthermore, when the closed path Y, has a direction assign to it, encirclement, if made can be in the clockwise direction or in the anti-clockwise direction.
Point A is encircled by Y by anticlockwise direction. We can say that the region inside the path is encircled in the prescribed direction and the region outside the path is not encircled.
Enclosed:
A point or region is said to be enclosed by a closed path if it is encircled in the counter clockwise direction, or the point or region lies to the left of the path (always), when the path is traveling in the prescribed direction.
The concept of enclosure is particularly useful, if only a portion of a closed path is shown.
In this example the shaded region is

Fig 23 Enclosure
Considered to be enclosed by the closed path Y. In other words, point A is enclosed by Y in fig a. But is not enclosed by Y in fig b. And for point B it is vice versa.
No of encirclements and enclosures:
For A line is cut once
For B line is cut twice
Fig 24 Encirclement and Enclosure with example
As it’s overlapping but 2 times in Same direction
When a point is encircled by a closed path Y, a no. N can be assigned to the no. Of times it is encircled. The magnitude of N can be determined by drawing an arrow around the closed path Y.
Taking an arbitrary point S, and moving around in clockwise direction and anti-clockwise direction respectively. We are getting a direction.
The path followed by S1 gives us the direction and this path which covers the total number of revolution travelled by this point S1 is N or the net angle is ‘ 2 π N ’.
For B = 2 = N for A = 1 = N
In this eg. Point A is encircled ones (or 2 π radians) by function Y and point B is encircled twice (or 4 π radians)all in clockwise direction.
In diagram b again A and B are encircled but in counter clockwise direction thus for this diagram A is enclosed one’s and B is enclosed twice.
By definition M is +ve for anticlockwise(direction) encirclement and –ve for clockwise encirclement.
OLTF G(S) = (S + Z1)(S + Z2)/(S + P1)(S + P2) H(S) = 1 - - (1)
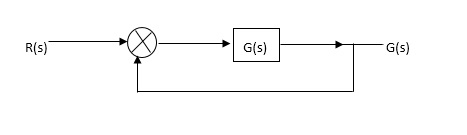
Fig 25 Unity feedback control system
CLTF G(S)/1 + G(S)
CE = 1 + G(S)
= 1 + (S + Z1)(S + Z2)/(S + P1)(S + P2)
CE = (S + P1)(S + P2) + (S + Z1)(S + Z2)/ (S + P1)(S + P2) - - (2)
Key takeaways:
# Zeros of characteristic equation is poles of CLTF (3 and 4).
For the closed loop system to be stable zeros of CE(i.e. poles of CLTF) should not be located at right half of the S-plane.
Consider a contour, which covers the entire right half of S-plane.
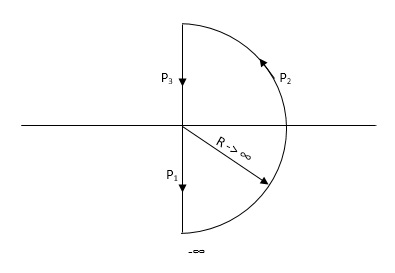
Fig 26 Contour For Right half of S-plane
P1 W(0 - ∞)
P2 RejR ∞
ϴ - π/2 to 0 to + π/2
P3 W(∞ to 0 )
If each and every point along the boundary of contour is mapped in q(S) where q(S) is 1+G(S)H(S)[CE]. The CE is drawn in S-domain. Now, as the CE: q(s) = 1 + G(S)H(S) contour is drawn into S-plane.
This q(S) contour may encircle the origin. Thus, the number of encirclement of q(S) contour with respect to origin is given by
N = Z – P
Where: Z1P zeros and poles of q(S)[CE]
N Total no of encirclement of origin
- Z1P Zeros and poles of CE in the right half of S-plane
** for the CL system to be stable Z=0 always.
Important:
Open loop System(stable): When OL system is stable P=0 i.e. no of poles on right half
N = Z – P
If P = 0
N = Z
- Now for CL system to be stable Z = 0
- N = 0
- i.e. q(s) contour should not encircle the origin.
Open loop system(unstable): Let P = 1 i.e. one OL pole is located in right half of S-plane i.e. OLTF is unstable.
As N = Z – P
N = Z – 1
For CL system to be stable the only criteria is (Z=0) i.e.
N = -1
Which means q(S) contour should encircle the origin one’s in CW direction.
Key takeaways:
(1). When OL system is unstable then corresponding CL will be stable only when q(S) contour will encircle origin in CW direction.
(2). The no of encirclements should be equal to no of open loop poles located in right half of S-plane.
** the no of encirclements(N) can also be calculated by using G(S) contour (instead of q(S) contour) but the reference is -1+j0 instead of 0+j0 i.e. the no of encirclements should be considered w.r.t -1+j0 and not with the origin.
Explanation Mapping
q(S) = 1 + G(S)
G(S) is always given to us, so we can relate G(S) with q(S).
G(S) = q(S) – 1
But q(S) can be drawn by adding 1 real part to the q(S).

Fig 27 Mapping
G(S) given then q(S) shift to right side.
Examples
Q1. For the transfer function below plot the Nyquist plot and also comment on stability?
G(S) = 1/S+1
Sol: N = Z – P (No pole of right half of S plane P = 0)
P = 0, N = Z
NYQUIST PATH:
P1 = W – (0 to - ∞)
P2 = ϴ(- π/2 to 0 to π/2 )
P3 = W(+∞ to 0)
Fig 28 Nyquist path
Substituting S = jw
G(jw) = 1/jw + 1
M = 1/√1+W2
Φ = -tan-1(W/I)
For P1: W(0 to -∞)
W M φ
0 1 0
-1 1/√2 +450
-∞ 0 +900
Path P2:
W = Rejϴ R ∞ϴ -π/2 to 0 to π/2
G(jw) = 1/1+jw
= 1/1+j(Rejϴ) (neglecting 1 as R ∞)
M = 1/Rejϴ = 1/R e-jϴ
M = 0 e-jϴ = 0
Path P3:
W = -∞ to 0
M = 1/√1+W2, φ = -tan-1(W/I)
W M φ
∞ 0 -900
1 1/√2 -450
0 1 00
The Nyquist Plot is shown in fig 29
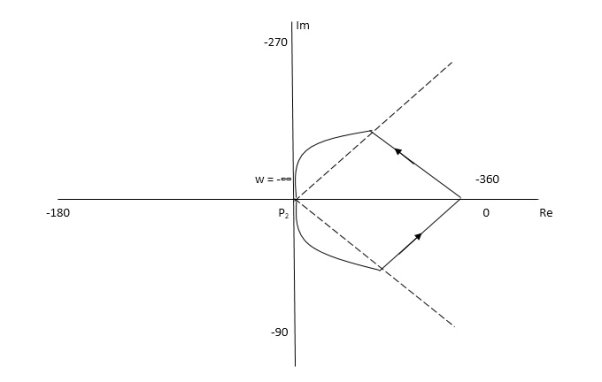
Fig 29 Nyquist Plot G(S) = 1/S+1
From plot we can see that -1 is not encircled so, N = 0
But N = Z, Z = 0
So, system is stable.
Q.2. For the transfer function below plot the Nyquist Plot and comment on stability G(S) = 1/(S + 4)(S + 5)
Soln: N = Z – P, P = 0, No pole on right half of S-plane
N = Z
NYQUIST PATH
P1 = W(0 to -∞)
P2 = ϴ(-π/2 to 0 to +π/2)
P3 = W(∞ to 0)
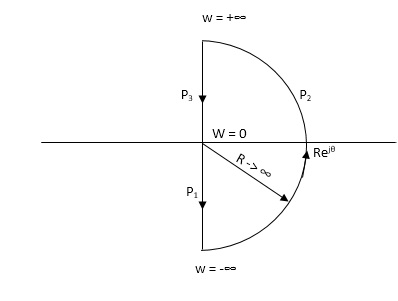
Fig 30 Nyquist Path
Path P1 W(0 to -∞)
M = 1/√42 + w2 √52 + w2
Φ = -tan-1(W/4) – tan-1(W/5)
W M Φ
0 1/20 00
-1 0.047 25.350
-∞ 0 +1800
Path P3 will be the mirror image across the real axis.
Path P2: ϴ(-π/2 to 0 to +π/2)
S = Rejϴ
G(S) = 1/(Rejϴ + 4)( Rejϴ + 5)
R∞
= 1/ R2e2jϴ = 0.e-j2ϴ = 0
The plot is shown in fig 31. From plot N=0, Z=0, system stable.
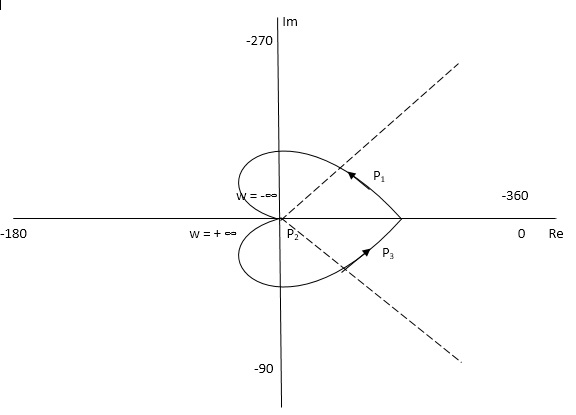
Fig 31 Nyquist Plot G(S) = 1/(S + 4)(S + 5)
Q.3. For the given transfer function, plot the Nyquist plot and comment on stability G(S) = k/S2(S + 10)?
Soln: As the poles exists at origin. So, first time we do not include poles in Nyquist plot. Then check the stability for second case we include the poles at origin in Nyquist path. Then again check the stability.
PART – 1: Not including poles at origin in the Nyquist Path.
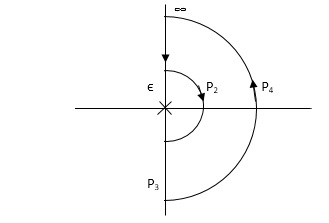
Fig 32 Nyquist Path
P1 W(∞ Ɛ) where Ɛ 0
P2 S = Ɛejϴ ϴ(+π/2 to 0 to -π/2)
P3 W = -Ɛ to -∞
P4 S = Rejϴ, R ∞, ϴ = -π/2 to 0 to +π/2
For P1
M = 1/w.w√102 + w2 = 1/w2√102 + w2
Φ = -1800 – tan-1(w/10)
W M Φ
∞ 0 -3 π/2
Ɛ ∞ -1800
Path P3 will be mirror image of P1 about Real axis.
G(Ɛ ejϴ) = 1/( Ɛ ejϴ)2(Ɛ ejϴ + 10)
Ɛ 0, ϴ = π/2 to 0 to -π/2
= 1/ Ɛ2 e2jϴ(Ɛ ejϴ + 10)
= ∞. e-j2ϴ [ -2ϴ = -π to 0 to +π]
Path P2 will be formed by rotating through -π to 0 to +π
Path P4 S = Rejϴ R ∞ ϴ = -π/2 to 0 to +π/2
G(Rejϴ) = 1/ (Rejϴ)2(10 + Rejϴ)
= 0
N = Z – P
No poles on right half of S plane so, P = 0
N = Z – 0
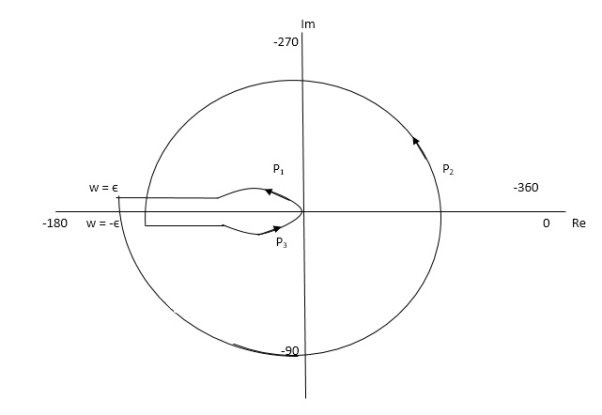
Fig 33 Nyquist Plot for G(S) = k/S2(S + 10)
But from plot shown in fig 32. It is clear that number of encirclements in Anticlockwise direction. So,
N = 2
N = Z – P
2 = Z – 0
Z = 2
Hence, system unstable.
PART 2 Including poles at origin in the Nyquist Path.
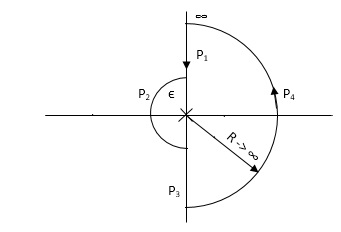
Fig 34 Nyquist Path
P1 W(∞ to Ɛ) Ɛ 0
P2 S = Ɛejϴ Ɛ 0 ϴ(+π/2 to +π to +3π/2)
P3 W(-Ɛ to -∞) Ɛ 0
P4 S = Rejϴ, R ∞, ϴ(3π/2 to 2π to +5π/2)
M = 1/W2√102 + W2 , φ = - π – tan-1(W/10)
P1 W(∞ to Ɛ)
W M φ
∞ 0 -3 π/2
Ɛ ∞ -1800
P3(mirror image of P1)
P2 S = Ɛejϴ
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10 + Ɛejϴ)
Ɛ 0
G(Ɛejϴ) = 1/ Ɛ2e2jϴ(10)
= ∞. e-j2ϴϴ(π/2 to π to 3π/2)
-2ϴ = (-π to -2π to -3π)
P4 = 0
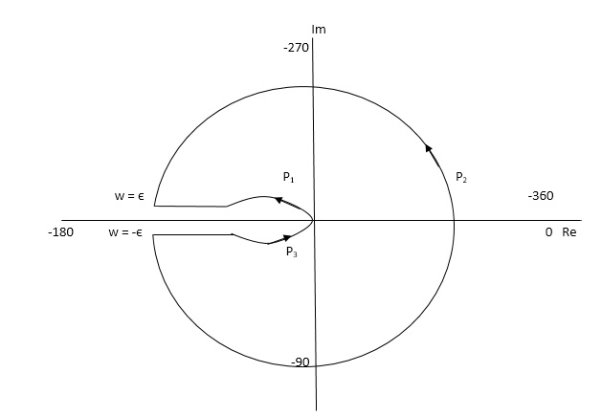
Fig 35 Nyquist Plot G(S) = k/S2(S + 10)
The plot is shown in fig 35. From the plot it is clear that there is no encirclement of -1 in Nyquist path. (N = 0). But the two poles at origin lies to the right half of S-plane in Nyquist path. (P = 2)[see path P2]
N = Z – P
0 = Z – 2
Z = 2
Hence, system is unstable.
Path P2 will be formed by rotating through -π to -2π to -3π
NOTE: The sign convention for angles is shown
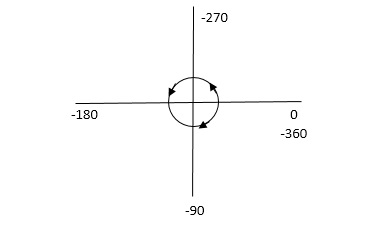
Fig 36 Sign for Angle Directions
Angles are considered –ve for anticlockwise directions and +ve for clockwise directions.
For open loop system number of poles o RHP are zero. So, the number of closed loop poles i.e zeros of Q(s) becomes
z=N+P
z=N
For open loop transfer function
G(s)H(s)= k/s(1+T1s)( 1+T2s)
The sinusoidal transfer function will be
G(jω)H(jω)=k/ jω(1+ jωT1) (1+ jωT2)
The polar plot will be
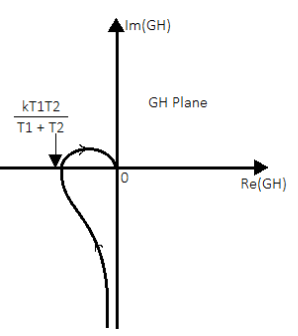
Fig 37 Polar Plot for G(s)H(s)= k/s(1+T1s)( 1+T2s)
The intersection of polar plot with real axis can be obtained by equating imaginary part of G(jω)H(jω) to zero.
G(jω)H(jω) = -k[ω(T1+T2)+j(1- ω2T1T2)]/ ω(1+ ω2T12)( 1+ ω2T22)
The imaginary part is zero when
1-ω2T1T2 = 0
ωpc = 1/√ T1T2
At ωpc the magnitude of G(jω)H(jω) is
| G(jω)H(jω)| = -k T1T2/ T1+T2
The given system is stable when number of encirclements of -1+j0 is zero.
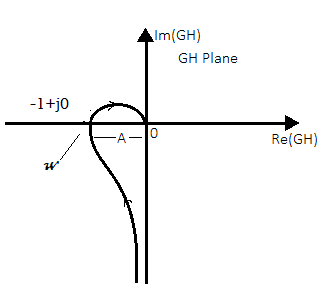
Fig 38 Finding GM of system from polar plot
Therefore, the condition for the system to be stable is k T1T2/ T1+T2<1.
When k < T1+T2/ T1T2 the point -1+j0 is not encircled by G(jω)H(jω) and system is stable. The gain is called critical gain kc= T1+T2/ T1T2.
For k<kc system is stable and when k=kc the plot passes through -1+j0 point which indicates the system has roots on jω-axis. For k>kc system is unstable as G(jω)H(jω) encircles the point -1+j0 once. There are two relative stability measurements which are
Gain Margin
From above figure we can say that at ω= ωpc the phase angle of 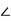 G(jω)H(jω) is 1800. The frequency at which the phase angle is 1800 is called as phase cross over frequency ωpc. Let A be magnitude at this frequency than if gain of the system is increased by 1/A the magnitude at ω= ωpc becomes 1 and hence G(jω)H(jω) locus passes through -1+j0 point and driving the system to the verse of instability. The gain margin can be defined as the reciprocal of the magnitude of open loop transfer function evaluated at the phase cross over frequency.
G(jω)H(jω) is 1800. The frequency at which the phase angle is 1800 is called as phase cross over frequency ωpc. Let A be magnitude at this frequency than if gain of the system is increased by 1/A the magnitude at ω= ωpc becomes 1 and hence G(jω)H(jω) locus passes through -1+j0 point and driving the system to the verse of instability. The gain margin can be defined as the reciprocal of the magnitude of open loop transfer function evaluated at the phase cross over frequency.
GM= 1/| G(j ωpc)H(j ωpc)|=1/A
 G(jω)H(jω) = - 1800
G(jω)H(jω) = - 1800
The GM in dB = -20logA.
Phase Margin
The frequency at which | G(jω)H(jω)|=1 is known as gain cross over frequency ωgc.As shown in figure bellow point A is the intersection of G(jω)H(jω)plot and the unit circle centred at the origin.
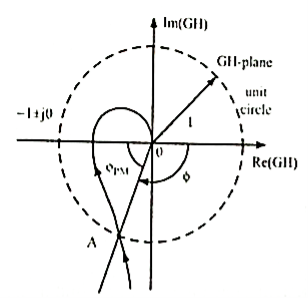
Fig 39 Finding PM of system from polar plot
Now draw a line connecting point A and origin and measure the phase angle between OA and positive real axis. The angle is known as phase angle of system at the gain cross over frequency.
 G(j ωpc)H(j ωpc)= ɸ
G(j ωpc)H(j ωpc)= ɸ
An additional phase lag ɸPM is introduced at this frequency then the phase angle  G(j ωpc)H(j ωpc) will become 1800 and the point A coincides with (-1+j0) driving the system to the verge of instability. This additional phase lag is known as phase margin. The value of phase margin can be obtained by
G(j ωpc)H(j ωpc) will become 1800 and the point A coincides with (-1+j0) driving the system to the verge of instability. This additional phase lag is known as phase margin. The value of phase margin can be obtained by
ɸPM= 1800 +  G(jω)H(jω) at ω= ωgc
G(jω)H(jω) at ω= ωgc
ɸPM= 1800 + ɸ
Key takeaways:
A zero GM in dB indicates critical stability. A positive GM indicates stability and a negative GM indicates instability.
For stable system PM is positive. A PM close to zero corresponds to highly oscillatory system.
Example
Q1) For the following system shown below find the phase margin and gain margin if the value of k=500by using Nyquist plot.
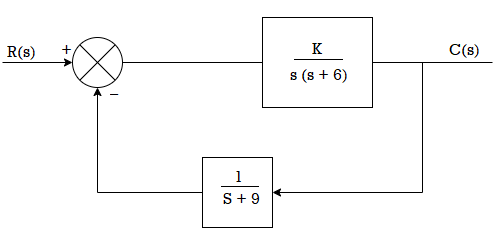
A1) G(s)H(s) = 500/s(s+6)(s+9)
The polar plot for above OLTF is shown in figure below.
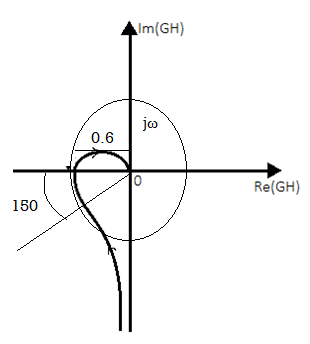
Fig 40 Polar Plot for given system
From figure we see A=0.6,
The GM in dB = -20logA.
= 4.43dB
PM = 1800-1650
= 150
Q2) For the system shown in figure, find the GM and PM using Nyquist plot for k=10. Find also range of k for stability?
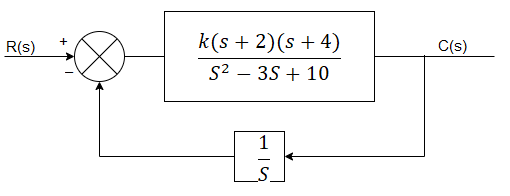
A2) The transfer function is G(s) H(s) = 10(s+2(s+4)/s(s2 – 3s+10)
As the OLTF is unstable system so PM and GM concepts cannot be applied.
G(jω) H(jω) = 10(jω+2) (jω+4)/ jω(-ω2 -3 jω+10)
| G(jω) H(jω)|= 10(√4+ω2)( √16+ω2)/ ω√[(10-ω)2+9 ω2]
 G(jω)H(jω) = -900 +tan-1(ω/2) + tan-1(ω/4) - tan-1 (-3ω/10- ω2)
G(jω)H(jω) = -900 +tan-1(ω/2) + tan-1(ω/4) - tan-1 (-3ω/10- ω2)
The polar plot for above system is shown below.
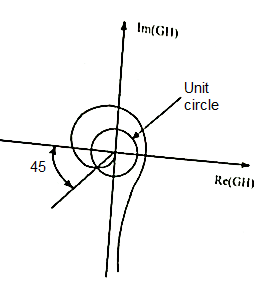
Fig 41 Polar plot for the given system
From figure we have A=2.6 and ɸ =-1350
The GM in dB = -20logA.
= -8.3dB
As GM is negative it indicates that system is open loop unstable.
PM = 1800-1650 = 450
3.6.1 Constant M Circle, Constant N Circle
Constant magnitude loci that are M-circles and constant phase angle loci that are N-circles are the fundamental components. The constant M and constant N circles in G (jω) plane can be used for the analysis and design of control systems. However, the constant M and constant N circles in gain phase plane are prepared for system design and analysis as these plots supply information with fewer manipulations. Gain phase plane is the graph having gain in decibel along the ordinate (vertical axis) and phase angle along the abscissa (horizontal axis).
The M and N circles of G (jω) in the gain phase plane are transformed into M and N contours in rectangular co-ordinates.
A point on the constant M loci in G (jω) plane is transferred to gain phase plane by drawing the vector directed from the origin of G (jω) plane to a particular point on M circle and then measuring the length in db and angle in degree. The critical point in G (jω), plane corresponds to the point of zero decibel and -180o in the gain phase plane. Plot of M and N circles in gain phase plane is known as Nichols chart /plot.
For Constant M Circle
For a system with unity feedback having transfer function
T(s)= G(s)/1+G(s)
Replace s=jω
T(jω) = G(jω)/1+G(jω)
But we can write G(jω)= X(jω)+jY(jω)
The closed loop transfer function T(s) is
T(jω) = X+jY/1+X+jY= Mejα
M= |X+jY|/|1+X+jY|
M2=X2+Y2/(1+X2) + Y2
Solving above equation we get
[X-(M2/1-M2)]2 + Y2 = ([M/1-M2)]2
This is equation of circle with centre (M2/1-M2),0 and radius M/1-M2
When M<1, M decreases the radius of the circle decreases and centres located on positive real axis shifts towards origin. When M=0 the radius becomes 0 and the centre (0,0). This is shown in figure above.
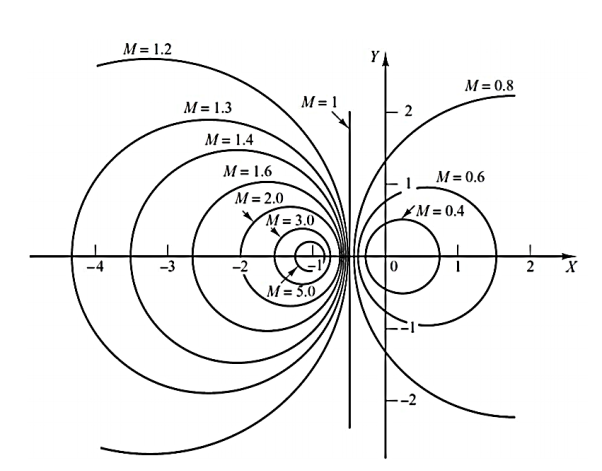
Fig 42 Constant M circle
Constant N Circle
The locus of constant phase of the closed loop system can be plotted in the G(jω) plane in same way as in constant M circle.
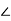 T(jω) = ɸ =
T(jω) = ɸ =  (X+jY)/(1+X+jY) = tan-1 (Y/X) – tan-1 (Y/1+X)
(X+jY)/(1+X+jY) = tan-1 (Y/X) – tan-1 (Y/1+X)
Solving above equation we get,
[X+1/2]2 +[Y-1/2N]2 =1/4 +[1/2N]2
This is equation of circle centred at (-1/2,1/2N) and radius √ (1/4) +(1/2N)2
Fig 43 Constant N circle
3.6.2 Nichols Chart
The Nichols plot is named after the American engineer N.B Nichols who formulated this plot. Compensators can be designed using Nichols plot. Nichols plot technique is however also used in designing of dc motor. This is used in signal processing and control design. Nyquist plot in complex plane shows how phase of transfer function and frequency variation of magnitude are related. • Angle of positive real axis determines the phase and distance from origin of complex plane determines the gain.
Advantages
- Gain and phase margin can be determined easily and also graphically.
- Closed loop frequency response is obtained from open loop frequency response.
- Gain of the system can be adjusted to suitable values.
- Nichols chart provides frequency domain specifications.
Disadvantage
Using Nichols plot small changes in gain cannot be encountered easily.
References
[1] I. J. Nagrath and M. Gopal, “Control Systems Engineering”, New Age International,
2009.
[2] K. Ogata, “Modern Control Engineering”, Prentice Hall, 1991
[3] M. Gopal, “Control Systems: Principles and Design”, McGraw Hill Education, 1997.
[4] B. C. Kuo, “Automatic Control System”, Prentice Hall, 1995.