Unit - 4

Time Value of Money

4.1 Time Value of Money-Interest – Simple and Compound, nominal and effective rate of interest, Cash flow diagrams, Principles of economic equivalence.

Interest rate is the percentage of principal that the lender charges for the use of the money. The principal is the loan amount.

Interest rate is the amount charged by the lender for the use of the asset, expressed as a percentage of the principal. Interest rates are listed on an annual basis, commonly known as the Annual Percentage Rate (APR). Borrowed assets can include cash, consumer goods, or large assets such as vehicles and buildings. Understand interest rates

Interest is essentially a rental or lease fee to the borrower to use the asset. For large assets such as vehicles and buildings, the lease rate can act as an interest rate. If the borrower is considered low risk by the lender, the borrower is usually charged a lower interest rate. If the borrowers are considered high risk, the interest rates they will be charged will be high. Risk is usually assessed when a lender sees a potential borrower's credit score, which is excellent if you want to qualify for the best loan

For loans, the interest rate applies to the principal, which is the amount of the loan. Interest rates are the rate of debt costs for borrowers and returns for credits.

When will interest rates apply?

Interest rates apply to most loan or borrowing transactions. The college tuition fees for the home where you purchased your personal debt, the start or fund business of a fund business, or the payment of your personal debt are as follows: Companies fund capital projects and obtain loans to expand their business by purchasing fixed and long-term assets such as land, buildings and machinery. Borrowed money will be repaid in one lump sum on a pre-determined date or in regular instalments.

The money repaid is usually more than the amount borrowed, as the lender needs compensation for the loss of money use during the loan period. The lender may be investing money during that period rather than offering a loan that would be generating income from the asset. The difference between the total repayment total and the original loan is of interest to be fulfilled. The interest charged will be applied to the principal amount.

Simple interest rate

The term simple interest is the interest rate commonly used by banks to calculate the interest rate charged to a borrower (compound interest is another common form of interest rate calculation used by lenders).

Like APR, simple interest calculation is the basis of the structure. The calculus used by banks when determining simple interest is:

Principal x interest rate xn = interest

For example, suppose you deposit $ 5,000 in a money market account that paid 1.5% for three years. Therefore, the interest earned by a bank saver over three years is $ 450 <x .03 x 3 = $ 450>.

Compound interest rate

Some lenders prefer the compound interest rate method, which means the borrower pays more for interest. Interest, also known as compound interest, applies not only to the principal, but also to the cumulative interest of the previous period. The bank assumes that at the end of the first year, the borrower bears the principal and interest of the year. The bank also assumes that at the end of the second year, the borrower bears principal plus first year interest plus first year interest.

The interest paid at the time of compounding is higher than the interest paid using the simple interest method. Interest is charged monthly on the principal, including accrued interest from the previous month. For short time frames, the calculation of interest is similar in both ways. However, as lending time increases, the gap between the two types of interest rate calculations increases.

Compound interest=p×[(1+interest rate)n−1]where:p=principaln=number ofCompounding periods​
 

How Interest Rate Differentials

The Forex market is the largest and most liquid market with nearly $ 5 trillion day traders. There are many drivers for a particular currency pair. The most attractive is the interest rate differential. The difference in short-term or long-term interest rates of the countries that make up a currency pair is used to create a forward rate and, in the long run, helps drive the direction of the currency pair. Most professional traders find that with the bond market. While keenly aware of how it affects the currency market, many novice traders are wondering how interest rates make up the forward curve of currency market dynamic interest rates.

When you buy or sell a currency pair, you buy one currency and sell another at the same time. Most of the global currency transactions are in the spot market. Spot market transactions will be settled within 2 business days. If you are interested in holding currency trading longer than 2 business days, you need to trade futures trading. Forward contracts add forward points to currency pairs that are traded for three days or more.

To calculate the forward rate, currency traders use the rate of interest differential. This is the difference in short-term interest rates for every of the countries that structure a currency pair. For example, if you buy a US dollar / yen currency pair, you will receive a US dollar interest rate and you will have to pay the Japanese short-term interest rate.

Certain things are added or subtracted from it. First, you need to determine which rate is higher. Currently, US dollar interest rates are above Japanese interest rates. Using the USD / JPY purchase example, you would deduct the forward points from the rate that offers the new rate that incorporates the forward points.

The main difference between simple interest and compound interest is time.

Let's say you invest $ 10,000 in a bank's money market account with a 4% interest rate. After the first year, you will earn $ 400 based on a simple interest calculation model. At the end of the second year, you'll make as much as $ 400 on your investment.

With compound interest, you also earn $ 400, which you will receive after the first year, just as you would with a simple interest model. However, after that, the interest rate earned will increase year by year.

For example, if you use the same $ 10,000 invested with a 4% rate of return, you will earn $ 400 in the first year and your total account value will be $ 10,400. Future total interest in the second year is not based on the original $ 10,000, but is now based on the total value of the account, or $ 10,400.

Each year, 4% interest starts on the basis of the added principal and increases on a compound basis year by year. This makes the investment worth more than if you calculated your investment using simple interest.

Nominal and effective rate of interest

Nominal and Effective Interest Rates Everything we’ve done up to this point is based on the compound interest formula:

F=P(1+i} ^n

If you examine the equations we’ve used to calculate the present and future values of cash flow series, you’ll find the compound interest formula embedded in all of them. For example,

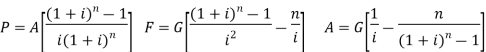
In these equations “i” is always the interest rate per compounding period and “n” is always the number of compounding periods separating F and P. For cash flow series “n” is also the number of arrows in the cash flow diagram, so the number of cash flows in the series must be equal to the number of compounding periods. In these cases, we say that the payment period (the amount of time between cash flows) is equal to the compounding period (the amount of time between interest payments).  We relax that requirement somewhat and look at cash flows that occur at some integer multiple of the compounding period (e.g., every other compounding period). Before we can do that, though, we have to introduce the concepts of nominal interest rates and effective interest rates.

For Example: A credit card company charges 21% interest per year, compounded monthly. What effective annual interest rate does the company charge?

r = 0.21 per year

m = 12 months per year

ia = [ 1 + (.21 / 12)]12 - 1

= [1 + 0.0175]12 - 1

= (1.0175)12 - 1 = 1.2314 - 1

= 0.2314 = 23.14%

It may be desired to find the effective interest rate for a period other than annual. In this case, adjust the period for "r" and "m" as needed. For example, if the effective interest rate per semi-annual period (every 6 months) is desired, then

r = nominal interest rate per 6 months

m = number of compounding periods per 6 months and the effective interest rate, isa, per semi-annual period, is:

isa = [ 1 + (r / m)]m - 1

Cash flow diagrams

Preface

In this comparison method, the cash flow of each option is reduced to zero time by assuming the interest rate i. The best alternative is then selected by comparing the present value of the alternatives, depending on the type of decision.

The sign of different amounts at different points in the cash flow diagram is determined based on the type of decision problem.

In this evaluation method, the coins go with the drift of every alternative is decreased to 0 time via way of means of assuming the hobby charge i. The satisfactory opportunity is then decided on via way of means of evaluating the prevailing price of the alternatives, relying at the kind of selection.

In revenue / profit-dominated cash flow diagrams, profit, revenue, and salvage value (all inflows into the organization) are assigned a positive sign. Costs (outflows) are assigned with a negative sign.

If it is decided to choose the alternative at the lowest cost, the alternative with the lowest present value will be chosen. On the other hand, if you choose the alternative with the highest profit, the alternative with the highest present value is selected.

Cash flow charts provide a visual representation of your income and expenses over a period of time. This figure consists of horizontal lines with markers at a series of time intervals. Costs and costs are displayed at the right time.

Please word that it's miles commonplace to reap coins go with the drift all through the yr-give up yr or on the give up of the yr (EOY). There are positive coins flows that aren't suitable and want to be treated differently. The maximum not unusual place is rent, that is generally received at the start of the coin’s length. There is different pay as you go flows which might be processed withinside the identical way.

For example, consider a truck that will be purchased for $ 55,000. It costs $ 9,500 each year to operate, including fuel and maintenance. The engine will need to be rebuilt for $ 22,000 within 6 years and will sell for $ 6,000 in the 9th year. The cash flow diagram is as follows.

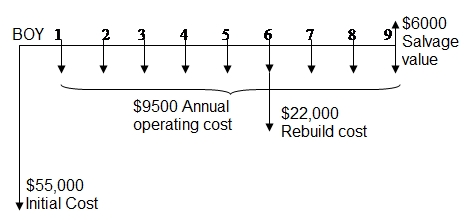
Note that the preliminary cost, the acquisition price, is recorded at the start of Year 1, now and again known as give up-of-yr 0, or EOY 0. Also, running and renovation fees simply will arise all through an yr, however they may be recorded at EOY, and so forth.

Principles of economic equivalence

Economic equivalence is a basic concept that underlies the calculations of the engineering economy. Before delving into the economics, think about the many types of equivalence we may use every day by moving from one scale to another. The following is an example of transfer between scales.

Length

12 inches=1 foot 3 feet = 1 yard 39.370 inches=1 meter

100 centimeters = 1meter  1000 meters =1 kilometer 1 kilometer=0.621 mile

Pressure:

1 atmosphere=1 newton/mete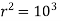pascal=1 kilopascal

Equivalence often involves more than one scale. Consider speed equivalence from 110 kilometres per hour (kph) to miles / minute using conversions between distance and time scales with three-digit accuracy.

Speed:

1 mile =1.609 kilometers 1 hour=60 minutes

110 kph=68.365 miles per hour (mph) 68.365 mph=1.139 per minute

Combine the four scales (hours in minutes, hours in hours, lengths in miles, and lengths in kilometres) to make these equivalent statements about velocity. Note that throughout these statements, the basic relationship of 1 mile = 1.609 kilometers and 1 hour = 60 minutes applies. If the basic relationship changes, the overall equivalence will fail.

Now consider economic equivalence.

Economic equivalence is the combination of interest rates and the time value of money to determine different amounts at different times when the economic values   are equal.

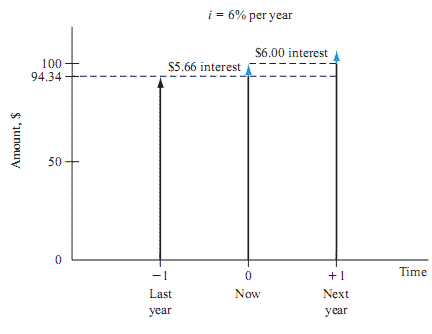
As an example, if the interest rate is 6% per year, today's (current) $ 100 is equivalent to $ 106 a year from today.

Incurred amount = 100 + 100 (0.06) = 100 (1 + 0.06) = $ 106

If someone offers you a gift of $ 100 today or $ 106 a year from today, there is no difference in the proposal you have accepted from an economic point of view. In both cases, it will be $ 106 a year from today. However, the two amounts are equal only if the annual interest rate is 6%. At higher or lower interest rates, $ 100 today is not equivalent to $ 106 a year from today.

In addition to future equivalence, the same logic can be applied to determine previous year's equivalence. The current total of $ 100 is equivalent to $ 100 1.06 = $ 94.34 a year ago, with an annual interest rate of 6%. From these figures, we can say: Last year it was $ 94.34, now it is $ 100, and a year later it is $ 106, which is equivalent at an annual interest rate of 6%. The fact that these sums are equal can be verified by calculating two interest rates for a one-year interest period.

and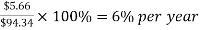

The cash flow chart in Figure shows the amount of interest required each year to equalize these three different amounts at 6% per year.

Key takeaways:

1. Interest rate is the percentage of principal that the lender charges for the use of the money.
2. Interest is essentially a rental or lease fee to the borrower to use the asset.
3. Interest rates apply to most loan or borrowing transactions.
4. The money repaid is usually more than the amount borrowed, as the lender needs compensation for the loss of money use during the loan period.
5. The term simple interest is the interest rate commonly used by banks to calculate the interest rate charged to a borrower (compound interest is another common form of interest rate calculation used by lenders).
6. The Forex market is the largest and most liquid market with nearly $ 5 trillion day traders.
7. Cash flow charts provide a visual representation of your income and expenses over a period of time.
8. There are certain cash flows that are not appropriate and need to be handled differently.
9. Economic equivalence is a basic concept that underlies the calculations of the engineering economy.
10. Economic equivalence is the combination of interest rates and the time value of money to determine different amounts at different times when the economic values   are equal.

4.2 Evaluation of Engineering Projects- Present Worth Method, Future Worth Method, Annual Worth Method, Internal Rate of return method, Cost benefit analysis for public projects.  

Present Worth Method

1. In this comparison method, the cash flow of each option is reduced to zero time by assuming the interest rate i
2. Then, depending on the type of decision, the best alternative is selected by comparing the present value of the alternatives.
3. In a cost-dominant cash flow diagram, costs (outflows) are assigned with a positive sign, and profits, revenues, salvage values (all inflows), etc. are assigned with a negative sign.
4. In revenue / profit-dominated cash flow charts, profit, revenue, and salvage value (all inflows into the organization) are assigned a positive sign. Costs (outflows) are assigned with a negative sign.

a. Revenue-Dominated Cash Flow Diagram

A generalized revenue-dominated cash flow diagram to demonstrate the present worth method of comparison is presented in Fig.

b. Cost-Dominated Cash Flow Diagram

A generalized cost-dominated cash flow diagram to demonstrate the present worth method of comparison is presented in Fig.

To compute the present worth amount of the above cash flow diagram for a given interest rate i, we have the formula

PW(i) = P + C1[1/(1 + i)1] + C2[1/(1 + i)2] + ... + Cj[1/(1 + i) j]

+ Cn[1/(1 + i)n] – S[1/(1 + i)n]

Example:

Alpha Industry is planning to expand its production operation. It has identified three different technologies for meeting the goal. The initial outlay and annual revenues with respect to each of the technologies are summarized in Table. Suggest the best technology which is to be implemented based on the present worth method of comparison assuming 20% interest rate, compounded annually.

Table

Solution

In all the technologies, the initial outlay is assigned a negative sign and the annual revenues are assigned a positive sign.

TECHNOLOGY 1

Initial outlay, P = Rs. 12,00,000

Annual revenue, A = Rs. 4,00,000

Interest rate, i = 20%, compounded annually

Life of this technology, n = 10 years

The cash flow diagram of this technology is as shown in Fig.

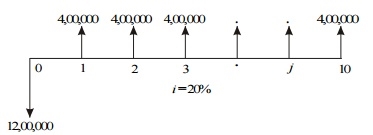
Cash flow diagram for technology 1.

The present worth expression for this technology is

PW (20%)1 = –12,00,000 + 4,00,000 (P/A, 20%, 10)

= –12,00,000 + 4,00,000 (4.1925)

= –12,00,000 + 16,77,000

= Rs. 4,77,000

TECHNOLOGY 2

Initial outlay, P = Rs. 20,00,000

Annual revenue, A = Rs. 6,00,000

Interest rate, i = 20%, compounded annually

Life of this technology, n = 10 years

The cash flow diagram of this technology is shown in Fig.

Cash flow diagram for technology 2. 

The present worth expression for this technology is 

PW (20%)2 = – 20,00,000      + 6,00,000 (P/A, 20%, 10)

= – 20,00,000       + 6,00,000 (4.1925)

=       – 20,00,000 + 25,15,500 

=       Rs. 5,15,500

TECHNOLOGY 3

Initial outlay, P = Rs. 18,00,000

Annual revenue, A = Rs. 5,00,000

Interest rate, i = 20%, compounded annually

Life of this technology, n = 10 years

The cash flow diagram of this technology is shown in Fig.

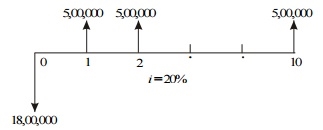
Cash flow diagram for technology 3.

The present worth expression for this technology is

PW (20%)3 = –18,00,000       + 5,00,000 (P/A, 20%, 10)

= –18,00,000 + 5,00,000 (4.1925)

=       –18,00,000 + 20,96,250

=       Rs. 2,96,250

From the above calculations, it is clear that the present worth of technology 2 is the highest among all the technologies. Therefore, technology 2 is suggested for implementation to expand the production.

Future Worth Method

1. The alternative future value comparison method calculates the future value of various alternatives.
2. Next, the net revenue with the highest future value or the net cost alternative with the lowest future value is selected as the best alternative for implementation.
3. Revenue-focused cash flow chart

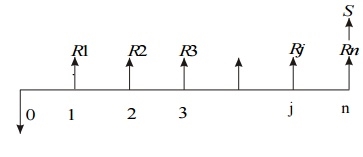
The figure shows a generalized revenue-focused cash flow diagram to show how to compare future values.

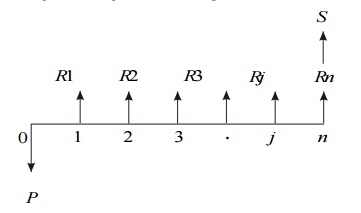
In Fig. P represents an initial investment, Rj the net-revenue at the end of the jth year, and S the salvage value at the end of the nth year.

The formula for the future worth of the above cash flow diagram for a given interest rate, i is

FW(i) = –P (1 + i) n + R1(1 + i) n–1 + R2(1 + i) n–2 + ...

+ R j (1 + i) n–j + ... + Rn + S

In the above formula, the expenditure is assigned with negative sign and the revenues are assigned with positive sign.

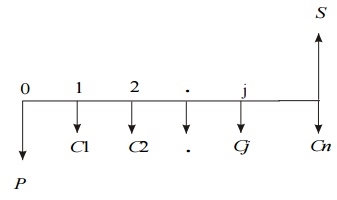
Ii. Cost-Dominated Cash Flow Diagram     

A generalized cost – dominated cash flow diagram to demonstrate the future worth method of comparison is given in fig

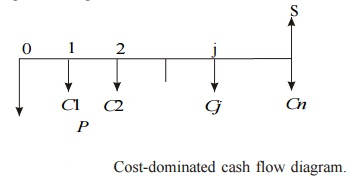
In Fig, P represents an initial investment, Cj the net cost of operation and maintenance at the end of the jth year, and S the salvage value at the end of the nth year.

The formula for the future worth of the above cash flow diagram for a given interest rate, i is

FW(i) = P (1 + i) n + C1(1 + i) n–1 + C2(1 + i) n–2 + ...  + Cj (1 + i) n–j + ... + Cn – S

EXAMPLE

Consider the following two mutually exclusive alternatives:

At i = 18%, select the best alternative based on future worth method of comparison.

Solution Alternative A

Initial investment, P = Rs. 50,00,000

Annual equivalent revenue, A = Rs. 20,00,000

Interest rate, i = 18%, compounded annually

Life of alternative A = 4 years

The cash flow diagram of alternative A is shown in Fig.

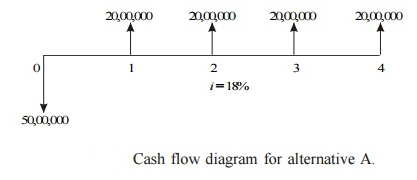
The future worth amount of alternative B is computed as

FWA (18%) = –50,00,000(F/P, 18%, 4) + 20,00,000(F/A, 18%, 4)

= –50,00,000(1.939) + 20,00,000(5.215)

= Rs. 7,35,000

Alternative B

Initial investment, P = Rs. 45,00,000

Annual equivalent revenue, A = Rs. 18,00,000

Interest rate, i = 18%, compounded annually

Life of alternative B = 4 years

The cash flow diagram of alternative B is illustrated in Fig.

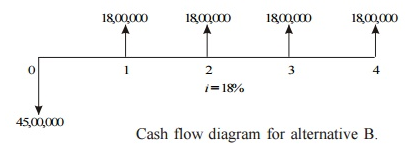
The future worth amount of alternative B is computed as

FWB (18%) = – 45,00,000(F/P, 18%, 4) + 18,00,000 (F/A, 18%, 4)

= – 45,00,000(1.939) + 18,00,000(5.215)

= Rs. 6,61,500

Annual Equivalent Method

1. The annual equivalence comparison method first calculates the annual equivalence cost or revenue for each alternative.
2. Next, the best alternative is chosen, which has the highest annual equivalent revenue for revenue-based comparisons or the lowest annual equivalent cost for cost-based comparisons.
3. Revenue-focused cash flow chart

Figure 1 shows a generalized revenue-controlled cash flow diagram to show the annual equivalence comparison method.

In Fig. P represents an initial investment, Rj the net revenue at the end of the jth year, and S the salvage value at the end of the nth year.

The first step is to find the net present worth of the cash flow diagram using the following expression for a given interest rate, i:

PW(i) = –P + R1/ (1 + i)1 + R2/ (1 + i)2 + ...

+ Rj/ (1 + i) j + ... + Rn/ (1 + i) n + S/ (1 + i) n

In the above formula, the expenditure is assigned with a negative sign and the revenues are assigned with a positive sign.

Ii. Cost-Dominated Cash Flow Diagram

A generalized cost-dominated cash flow diagram to demonstrate the annual equivalent method of comparison is illustrated in Fig.

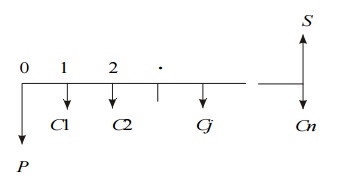
In Fig, P represents an initial investment, Cj the net cost of operation and maintenance at the end of the jth year, and S the salvage value at the end of the nth year.

The first step is to find the net present worth of the cash flow diagram using the following relation for a given interest rate, i.

PW(i) = P + C1/ (1 + i)1 + C2/ (1 + i)2 + ...

+ Cj/ (1 + i) j + ... + Cn/ (1 + i) n – S/ (1 + i) n

EXAMPLE

A company provides a car to its chief executive. The owner of the company is concerned about the increasing cost of petrol. The cost per litre of petrol for the first year of operation is Rs. 21. He feels that the cost of petrol will be increasing by Re.1 every year. His experience with his company car indicates that it averages 9 km per litre of petrol. The executive expects to drive an average of 20,000 km each year for the next four years. What is the annual equivalent cost of fuel over this period of time? If he is offered similar service with the same quality on rental basis at Rs. 60,000 per year, should the owner continue to provide company car for his executive or alternatively provide a rental car to his executive? Assume i = 18%. If the rental car is preferred, then the company car will find some other use within the company.

Solution

Average number of km run/year = 20,000 km

Number of km/litre of petrol = 9 km

Therefore,

Petrol consumption/year = 20,000/9 = 2222.2 litre

Cost/litre of petrol for the 1st year = Rs. 21

Cost/litre of petrol for the 2nd year = Rs. 21.00 + Re. 1.00

= Rs. 22.00        

Cost/litre of petrol for the 3rd year = Rs. 22.00 + Re. 1.00 = Rs. 23.00 

Cost/litre of petrol for the 4th year = Rs. 23.00 + Re. 1.00 = Rs. 24.00 

Fuel expenditure for 1st year = 2222.2    21      = Rs. 46,666.20

Fuel expenditure for 2nd year = 2222.2    22      = Rs. 48,888.40

Fuel expenditure for 3rd year = 2222.2     23      = Rs. 51,110.60

Fuel expenditure for 4th year = 2222.2     24      = Rs. 53,332.80

The annual equal increment of the above expenditures is Rs. 2,222.20

(G). The cash flow diagram for this situation is depicted in Fig.

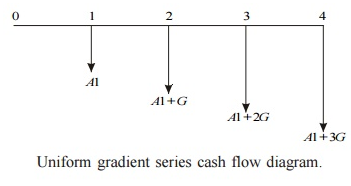
In Fig., A1 = Rs. 46,666.20 and G = Rs. 2,222.20

The proposal of using the company car by spending for petrol by the company will cost an annual equivalent amount of Rs. 49,543.28 for four years. This amount is less than the annual rental value of Rs. 60,000. Therefore, the company should continue to provide its own car to its executive.

Internal Rate of return method

The rate of return of a cash flow pattern is the interest rate at which the present value of that cash flow pattern decreases to zero.

This comparison method calculates the rate of return for each option. The most profitable alternative is then selected as the best alternative.

Figure 1 shows a generalized cash flow diagram showing how to compare rates of return.

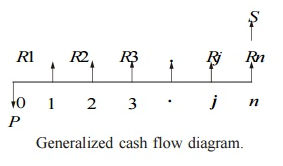
In the above cash flow diagram, P represents an initial investment, Rj the net revenue at the end of the jth year, and S the salvage value at the end of the nth year.

The first step is to find the net present worth of the cash flow diagram using the following expression at a given interest rate, i.

PW(i) = – P + R1/ (1 + i)1 + R2/ (1 + i)2 + ...

+ Rj/ (1 + i) j + ... + Rn/ (1 + i) n + S/ (1 + i) n

EXAMPLE

A person is planning a new business. The initial outlay and cash flow pattern for the new business are as listed below. The expected life of the business is five years. Find the rate of return for the new business.

Solution

Initial investment = Rs. 1,00,000 Annual equal revenue = Rs. 30,000 Life = 5 years

The cash flow diagram for this situation is illustrated in Fig.

The present worth function for the business is

PW(i) = –1,00,000 + 30,000(P/A, i, 5)

When i = 10%,

PW (10%) = –1,00,000 + 30,000(P/A, 10%, 5)

= –1,00,000 + 30,000(3.7908)

=      Rs. 13,724.

When i = 15%,

PW (15%) = –1,00,000 + 30,000(P/A, 15%, 5)

=    –1,00,000 + 30,000(3.3522)

=    Rs.  566.

When i = 18%,

PW (18%) = –1,00,000 + 30,000(P/A, 18%, 5)

=    –1,00,000 + 30,000(3.1272)

=    Rs. – 6,184

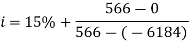
Therefore, the rate of return for the new business is 15.252%.

Cost benefit analysis for public projects

Meaning of cost-benefit analysis:

Sector companies, primarily driven by profit motives, only have an internal direct impact (i.e., the cash flow they incur and the costs they have to bear) when making business decisions. Consider and do not take a longer and broader view of their activities from a social point of view. However, public enterprises and non-profits must take on the broader social impact of their resource allocation and investment decisions. That is, it takes into account both internal (direct) and external (indirect) impacts of business decisions.

An analytical model called cost-benefit analysis is used to analyze the broader impact of resource allocation and investment decisions. The correct understanding is the social cost-benefit analysis of investment projects, but the word "social" is often omitted. Therefore, the social cost-benefit analysis estimates both the direct and indirect costs of a project to society and the direct and indirect benefits of a project. These indirect costs and benefits are often referred to as externalities. Therefore, in addition to direct costs and benefits, the analysis of social costs and benefits takes into account the externalities of the investment project.

Therefore, the cost-benefit analysis is the counterpart of the capital budgeting method used to evaluate the desirability of investment projects and programs in the public sector and to evaluate investment projects by private companies. Pioneers of cost-benefit analysis technology, Perst and Survey, explain the essence of cost-benefit analysis and write: And a broader perspective (in the sense of allowing side effects of many types and many people, industries, regions, etc.), that is, of all the costs and benefits associated with it (in the sense of seeing the effects of the distant and near future). Means enumeration and evaluation. "

When estimating the social cost of a project, it is important to note that the market price of the resource is not used, as it is generally distorted. They are distorted due to government tax impositions, or market flaws or the monopoly of resource owners. Instead, social cost-benefit analysis uses shadow prices that reflect the value of opportunity cost or the true rarity of the resource.

It is worth noting that public sector companies and non-profits face the same resource allocation and investment issues as the private sector. However, when companies in the public sector have a broader perspective and make decisions about them, taking into account both internal and external influences (i.e., externalities) of the decision, the private sector leads only to the consideration of profits. He adopts a narrow view and considers only the internals, ignoring external effects that may be harmful or beneficial, the effects of business decisions. Therefore, cost-benefit analysis is not just about the internal benefits and costs of the investment projects you carry out.

Instead, the cost-benefit analysis enumerates and evaluates all social benefits and all social costs of a project or spending program. This is an investment project that considers only private costs and interests, as opposed to the capital budgeting method used by private companies. Therefore, citing Todalo and Smith, "the usual criteria for commercial profitability that guide private investors' investment decisions may not be a good guide to public investment decisions, so a social cost-benefit analysis is needed. Since private companies are interested in maximizing private profits, they usually only consider variables that affect the balance of net profits. Both receipts and profits are inputs and outputs. It is evaluated at the prevailing market price of the investment. "

According to the social cost-benefit analysis, the actual income or income from the project is truly both the social benefit from the project and the expenditure incurred on the market-priced input used as the true social cost. Not reflected. In addition, in the calculation of social costs and benefits, governments or planners take into account the external effects of public investment projects (both external and uneconomical), while private companies ignore them in project valuation.

From the above, the difference between private costs and benefits of social costs and benefits, and investment decisions based on private costs and benefits will lead to inappropriate decisions and therefore will not maximize social welfare. Become. In addition, we believe that the social cost-benefit analysis approach can reach social cost-benefit by adjusting market prices appropriately.

What's more, the profits from investment projects will come primarily in future years, and the costs will come in the long term in the future, so it is the discounted social benefits that are compared to determine the desirability of the project. And discounted social costs. However, in order to discount the social costs and benefits of investment projects, it is the social discount rate that is used to obtain the net present value rather than the market interest rate.

Use of cost-benefit analysis:

Cost-benefit analysis techniques are especially used when a long and broad view of the effectiveness of a particular project or spending program is required. Cost-benefit analysis is commonly used when the economic impact of a project or investment spending program or policy change occurs in the future, as is the case with private sector capital budgets. However, unlike private sector capital budgets, cost-benefit analysis seeks to estimate all direct and indirect spill over effects.

Cost-benefit analysis is used to assess whether to accept or reject a particular project or a particular public spending program. To do so, both direct and indirect benefits of the project or a particular public spending program, as well as the costs incurred by the project over the years, are estimated. Then use the appropriate discount rate from a social perspective to estimate the present value of both future benefits and costs.

From the above, cost-benefit analysis is a way to evaluate public projects and investment programs to make decisions about the desirability of the projects being implemented. Therefore, it is used to evaluate large public investment schemes such as dam and airport construction, disease management (such as malaria control programs), defense and safety planning, health, education and research spending.

General procedure for performing cost-benefit analysis:

There are no simple rules or procedures that a government or public agency should follow to perform a cost-benefit analysis. Through cost-benefit analysis, we try to find the social profitability of the project. The calculation of social profitability should take into account both direct social costs and benefits, and measure both social benefits and social costs (that is, the inputs used directly in the project). Actual costs and the direct output from them) and overhead costs (e.g., external uneconomic) and indirect benefits (e.g., creating employment opportunities).

Social profitability is determined by the difference between social benefits (both direct and indirect) and social costs (both direct and indirect).

The entire process of calculating social profitability or social costs and benefits can be divided into five steps:

1. Designation of social objective function:

The first step in performing a cost-benefit analysis is to specify the social objective function that needs to be maximized. In this objective function, weights are assigned to different profits (for example, increased per capita consumption, increased employment, desirable income distribution). These weights reflect the importance given to the various benefits of the project.

2. Identify different benefits and costs:

The second step in cost-benefit analysis is to identify and list all direct and indirect benefits and costs of an investment project. The direct benefit of a project can be measured by the additional quantity of goods and services produced when the project is implemented, compared to when the project is not implemented.

Therefore, the direct advantage of irrigation projects is the amount of additional crops produced, minus additional costs, in the form of more labor, seeds and equipment used compared to unirrigated land. Is. Direct costs, on the other hand, include capital equipment, installed machinery, capital costs for land acquired to carry out and implement the project, and operational and maintenance costs incurred over the life of the project.

In addition to the direct impact of an investment project, there is always an indirect or external impact. These indirect or external beneficial effects fall into two types: (1) actual or technical effects and (2) monetary effects. Actual external benefits may include cost savings incurred by other government programs.

For example, the construction of irrigation dams can lead to reduced floods and soil erosion, reducing government spending on flood control and soil erosion prevention programs. Such actual indirect benefits are counted in cost-benefit studies.

Indirect (external) monetary benefits, on the other hand, are generally not included in the cost-benefit study benefits and cost listings. These external financial benefits come in the form of increased business volumes or increased land prices as a result of project implementation.

Therefore, the areas of Delhi near the metro railroad routes have caused land prices to rise in these areas. In addition, the transaction volume of shops and restaurants around the metro is increasing. These indirect or external monetary benefits are distributive and are not included in the Metro Railroad Cost-Benefit Study.

Similarly, indirect multiplier effects and induced investment effects resulting from government investment projects are generally not counted as they occur regardless of whether the investment is from the public or private sector (). Except for some special circumstances).

For example, if the purpose of a government investment program is regional development, implementing a regional investment project can trigger regional investment. Create a multiplier effect on income and job creation and reduce unemployment in the region. Since regional development forms part of the maximized social objective function, some include them in the cost-benefit study of regional investment programs.

3. Evaluation of social benefits and costs:

The third step in the social cost-benefit analysis is to measure the social value of profits, that is, the social cost of the output (both goods and services) produced by the project and the inputs used in the project.

Shadow prices (also known as accounting prices) are used instead of market prices to evaluate the output of goods and services. Since the market price is different from the true social value, the shadow price is used to measure the social value of the output. In fact, the greater the difference between shadow and market prices, the greater the need for social cost-benefit analysis to determine public investment.

Similarly, cost-benefit analysis measures costs using the shadow price of the input or factor used in the project. It is worth noting that the shadow price of an input or factor is a value overlooked by those opportunity costs, or the factors and resources used for initial capital investment and production during the life of the project. This is because resources need to be drawn from other activities in order to carry out the proposed project. For example, when implementing an irrigation project, 50% of the required workforce will be withdrawn from the unemployed class.

The social opportunity cost of such labor is zero and the employed workers are paid market wages, which should be calculated in the cost-benefit analysis. The same is true for idle land used for projects. Opportunity cost of idle land is zero because there is no alternative use. This is true despite the fact that the government actually has to pay compensation to the landowners to acquire this idle land. This compensation only affects the distribution of profits from the project to land use, not the social cost of the project.

All profits and costs (both internal and external) for the life of the project must be discounted to obtain the present value. In this regard, we must also make difficult decisions about appropriate social discount rates that discount future benefits and costs in order to find present value.

Another important issue in calculating social benefits and costs is measuring a common unit of social benefits and costs (also known as numeraire), especially if the country has a trade relationship with another country in the world. And to express. You need to buy and sell overseas. This common unit is needed to be able to compare domestic and foreign products. There are two main approaches to finding a common account unit. The first approach is the UNIDO approach and the second approach is the Little-Mirrlees approach.

In UNIDO's approach, profits and costs are measured at domestic market prices using consumption as a numeraire. In addition, this approach uses product shadow prices and factors to adjust for differences between market prices and social value. In addition, shadow exchange rates are used to allow comparison of domestic and international resources.

In the Little-Mirrlees approach, project profits and costs are measured at global prices, so they need to represent opportunity costs for outputs and inputs. Using world prices to measure profits and costs helps avoid the use of shadow exchange rates. In addition, the Little-Mirrlees approach uses forex public savings as the numéraire instead of consumption.

In short, the benefits and costs of this approach are valued in foreign exchange terms. However, this does not mean that the project account is held in foreign currency, only that the value in the project valuation report is recorded in the forex equivalent to estimate the amount of forex earned by the project. Means.

It should be noted that both the UNIDO and Mirrlees approaches face some measurement problems.

4. Find social discount rates: 

In cost-benefit analysis, the next step is to choose the right social discount rate. Since the benefits of investment projects are mainly in the future and the costs will be incurred for a long time in the future, it is discounted social benefits and discounts that are compared to determine the social desirability of the project. It is a social cost.

For this, we need a social discount rate. Private sectors are used to discount future profits and costs when calculating market interest rates for commercial profitability. However, when it comes to the social profitability of public sector investments, market interest rates are not appropriate for discounting future social benefits and costs.

So why is the social discount rate different from the market interest rate? Individuals want to live for a certain number of years, so they are discounting the future at higher interest rates that are reflected in market interest rates. Meanwhile, planners and governments in developing countries want to look longer and more important to the consumption and welfare of future generations, so lower discounts are needed to discount the flow of future social benefits. Use rate. And cost. Both are evaluated using shadow prices. Therefore, Todaro and Smith write: The higher the future benefits and costs are valued in the government's planning scheme, the lower the social discount rate, for example, if the government also represents future fatal citizens. "

5. Criteria for selecting a project:

Finally, the government must decide whether to accept or reject the investment project. To do this, we need criteria. The most commonly used standard is the net present value (NPV) standard. To use this criterion, you need to find the net present value of the proposed project using the following formula:

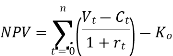
Where Vt is the flow of social benefits measured using the shadow price of the goods produced, Ct is the social cost of the input measured by the shadow price (i.e., opportunity cost), and rt is the social discount rate., Ko is a social cost. Of investment in the project.

Currently, investment projects are economically profitable from a social point of view if the net present value (NPV) of the project using the social discount rate is positive (that is, above zero). In other words, the proposed investment project must be accepted for investment if the present value (PV) of the project exceeds the current social cost of initial capital investment (K0).

Importance of cost-benefit analysis:

Social cost-benefit analysis is very important for development planning in developing countries. An important advantage of cost-benefit analysis is that it can guide investment decisions, especially in the public sector. Based on the cost-benefit analysis, given the resource constraints, the government can choose the most beneficial of them. Governments can also use social cost-benefit analysis to assess the effectiveness of private investment projects. This helps governments develop policies to support or discourage private investment.

Governments can support private investment projects by providing subsidies or provide financial support through financial institutions. Governments can discourage them by imposing taxes if their social costs exceed the social benefits of private investment.

The importance of cost-benefit analysis is better recognized when we consider that alternative methods of resource allocation are market mechanisms that use market prices for goods and services that do not reflect the true social benefits and costs of investment projects. Social cost-benefit analysis considers an increasingly broad range of social benefits and costs that incorporate both direct and indirect effects of investment.

Quoting Seawall’s words, "Publicly funded project valuation costs to recognize that the market price and factor of production of goods are not, and to allocate resources in the most beneficial way for society. Benefit analysis methods are recommended. Current levels of savings, given that they inevitably reflect their respective social values   and costs, and that society is interested not only in current but also in future consumption levels. May not be optimal. "

Key takeaways:

1. Present worth comparison method, the cash flow of each option is reduced to zero time by assuming the interest rate i
2. The alternative future value comparison method calculates the future value of various alternatives.
3. The annual equivalence comparison method first calculates the annual equivalence cost or revenue for each alternative.
4. The rate of return of a cash flow pattern is the interest rate at which the present value of that cash flow pattern decreases to zero.
5. Sector companies, primarily driven by profit motives, only have an internal direct impact (i.e., the cash flow they incur and the costs they have to bear) when making business decisions.
6. An analytical model called cost-benefit analysis is used to analyze the broader impact of resource allocation and investment decisions. The correct
7. According to the social cost-benefit analysis, the actual income or income from the project is truly both the social benefit from the project and the expenditure incurred on the market-priced input used as the true social cost.
8. Cost-benefit analysis techniques are especially used when a long and broad view of the effectiveness of a particular project or spending program is required.
9. There are no simple rules or procedures that a government or public agency should follow to perform a cost-benefit analysis.
10. The first step in performing a cost-benefit analysis is to specify the social objective function that needs to be maximized.
11. In cost-benefit analysis, the next step is to choose the right social discount rate.
12. Finally, the government must decide whether to accept or reject the investment project
13. Social cost-benefit analysis is very important for development planning in developing countries. An important advantage of cost-benefit analysis is that it can guide investment decisions, especially in the public sector.

4.3 Depreciation – Depreciation of capital asset, Causes of depreciation, Methods of calculating depreciation – Straight line method, Declining balance method, SOYD method, After tax comparison of projects.

Depreciation of capital asset

In accounting terms, depreciation is described as a scientific manner to lessen the recorded value of a set asset till the price of the asset turns into 0 or negligible.

Examples of fixed assets include buildings, furniture, office equipment and machinery. Land is the only exception that cannot be depreciated, as the value of land increases over time.

Depreciation reflects part of the cost of a fixed asset in the revenue generated by the fixed asset. This is mandatory under the matching principle, as revenue is recorded with the associated costs during the accounting period in which the asset is used. This will help you get a complete picture of your revenue-generating transactions.

Depreciation example – When a delivery truck buys a company at the cost of Rs. At 100,000, if the expected truck usage is 5 years, the company may depreciate the asset as Rs as depreciation expense. 20,000 people every year for 5 years.

Depreciation can be defined as a measure of the depletion of an asset's lifetime due to any cause during a particular time period. -Spicer and Pegler.

“Depreciation is a measure of the consumption, consumption, or other loss of value of a depreciable asset resulting from use, time wasted, or obsolescence due to changes in technology or market. During that time, you will be assigned to charge a significant portion of the depreciation amount for each accounting period. Depreciation expense includes the depreciation of assets with a predetermined useful life. "

-Accounting Standard-6 (revised), issued by ICAI.

Depreciation features:

(i) Depreciation is a decline in the value of fixed assets (excluding land). The decline in the value of an asset is inherently permanent. Once shrunk, it cannot be restored to its original value.

(ii) Depreciation is a gradual and continuous process because the value of an asset decreases due to the use of the asset or the expiration of time.

(iii) It is not an asset valuation process. This is the process of allocating the cost of an asset to its lifetime.

(iv) Depreciation reduces the book value, not the market value of an asset.

(v) Depreciation is only used for property, plant and equipment. It is not wont to waste intangible assets like amortization of goodwill and depletion of natural resources.

The calculation of depreciation expense for the accounting period is affected as follows:

(I)                The actual cost of the asset

(II)             Estimated useful life of the asset

(III)           Estimated residual value of the asset.

It is worth mentioning here that of the three factors, two are based on mere estimation and only one is actually based. Therefore, the depreciation calculation is an estimated loss on the value of the asset, not the actual exact reduction in the value of the asset.

The following is a detailed description of each of the above elements.

1. Actual cost of the asset:

The actual cost or acquisition cost means the acquisition cost of the asset and includes all incidental costs required to return the asset to its current state and location. Examples of such costs are installation costs, internal transportation, or capital-based costs incurred to improve such assets.

2. Estimated useful life of the asset:

The estimated useful life of an asset is one of the following:

(I) The period during which the depreciable asset is expected to be used by the entity or

(II) The number of production or similar units expected to be derived from the use of assets by a company.

3. Estimated residual value or scrap value of the asset:

The salvage price or scrap price is the anticipated price that can be found out while an asset is offered or exchanged on the quit of its predicted beneficial existence. If residual price is vital, it must be taken into consideration withinside the depreciation calculation. However, insignificant residual price may be left out withinside the depreciation calculation.

Depreciation is an ongoing process, but we do not record depreciation daily. In fact, the total depreciation expense charged on an asset is the prepaid expense paid by the entity at the time of acquisition of the asset.

In other words, this expense should be treated like a deferred expense, and only adjustment entries should be passed each year to claim reasonable and appropriate depreciation for income statement revenue.

Here are some other factors that influence the measurement of depreciation:

(I)                Original cost of the asset: The cost includes all costs incurred to acquire the asset. In other words, the purchase price includes shipping and installation costs, if any.

(II)             When an asset is added during the year, taking into account the date the addition was made.

(III)           Estimated useful life of the asset.

(IV)          Scrap or residual value of an asset.

(V)             Obsolescence, that is, the possibility of assets becoming obsolete

(VI)          Repairs and updates.

(VII)        Operator skills to handle assets.

(VIII)     Legal provisions or other restrictions related to depreciation.

(IX)           Working hours of the asset.

Causes of depreciation

Top 7 Causes of Depreciation

1. Due to wear during use of assets

This is one of the main reasons for asset depreciation. Continued use of assets causes most assets to wear or deteriorate. Plants and machines used in the production of goods, buildings, vehicles, etc. As with the machines used in production, the continuous use and operation of the machine reduces the work or capacity of the machine over time. The value of the machine also diminishes in the market. Therefore, in order to show the financial position of a company fairly, it is necessary to reduce the proportional value of the machines listed in the books.

2.     Compliance with accounting standards applicable to the entity

In accordance with the applicability of accounting standards to companies, companies must comply with the provisions contained in the standards. This is done according to the concept of matching that must be followed in the accounting of an entity. According to the concept of matching, depreciation is charged for each, as income through assets is also in the period listed in the books above.

3.     Technological advances in supplementary assets in the market

Value of fixed assets

When new upgraded versions of assets with better technological sophistication are available on the market, the assets used by the enterprise will gradually decrease, providing more benefits to customers compared to older discontinued versions of assets. To do. In such cases, the requirements for old assets will gradually diminish and the recoverable amount in the market will also diminish. Therefore, the value of an asset must be presented financially in a fair or reasonable amount.

4.     Use of the provided life of the asset

For fixed assets, the useful life of the asset is provided in units of consumption so that the asset "X" runs for 10,000 hours. Therefore, the cost of an asset is allocated according to consumption or hourly usage.

5.     Amortization of assets by license or usage period

Some assets, such as licenses, patents, copyrights, and leasehold rights, can only be used for a specified period of time. Over that time, the asset was unavailable. Therefore, that cost must be allocated or amortized according to the age of the asset. At the end of the validity period, the asset must be amortized from the books.

6.     Depreciation must be done to waste assets according to resource extraction

When wasting assets

Like coal mines, oil wells, etc. are amortized and used according to the extraction of natural resources made from them during the period. For such types of wasted assets, the resources that an entity can extract from such assets for use by the organization are limited. During each period, the depreciation of the asset during that period is considered according to the estimated total amount extracted from the wasted assets and the amount already extracted.

7.     The absolute need to maintain fixed assets for proper asset productivity

The plants and machines used by manufacturing companies to manufacture products require regular maintenance over a period of time to gain full-time productivity from the use of such machines. Even after a period of time, some important parts of the machine need to be replaced with new parts. Therefore, you must charge depreciation so that future replacement parts are properly accounted for and amortized over their useful lives.

Methods of calculating depreciation – Straight line method

Straight line method

What is the straight-line method?

The straight-line technique is the default technique used to lightly understand the sporting quantity of constant belongings over their beneficial lives. This is used whilst there may be no specific sample in how an asset is used over time. The straight-line technique is the perfect depreciation technique to calculate and is relatively advocated to be used because it reasons few calculation errors. The manner for flat-price calculation is as follows.

1. Determines the initial cost of an asset recognized as a fixed asset.
2. Subtract the estimated residual value of the asset from the amount recorded in the books.
3. Determines the estimated useful life of an asset. It is easiest to use the standard useful life for each class of asset.
4. Divide the estimated useful life (yearly) by 1 to calculate the depreciation rate using the straight-line method.
5. Multiply the depreciation rate by the cost of assets (minus salvage value).
6. Once calculated, depreciation expense is recorded in accounting records as a depreciation expense account and a credit to the accumulated depreciation account. Accumulated depreciation is against assets. That is, it is paired with the fixed asset account and the depreciation is reduced.

Formula:

Depreciation = (Asset Cost – Net Residual Value) / Service Life

Depreciation rate = (annual depreciation cost x 100) / cost of capital

Straight-line Journal Entries:

1. Purchase of Assets A / c Dr. Xx

To cash / bank / creditor A / cxx

(Purchasing assets)

2. Depreciation of assets A / c Dr. Xx

To asset A /cxx

(Assets are subject to depreciation)

3. Transfer depreciation gains / losses A / c Dr. Xx

To depreciation of asset A / cxx

(Asset depreciation is transferred to the profit and loss account)

Example 1

Pensive Corporation will purchase a Procrastinator Deluxe machine for $ 60,000. It has an estimated salvage value of $ 10,000 and a useful life of 5 years. Pensive calculates the machine's annual flat-rate depreciation as follows:

Solution

$ 60,000 Purchase Cost – $ 10,000 Estimated Residual Value = $ 50,000 Depreciable Asset Cost

1/5-year useful life = 20% annual depreciation rate

20% depreciation rate x $ 50,000 depreciation asset cost = $ 10,000 annual depreciation

Declining balance method

The various depreciation methods are based on mathematical formulas. This formula is derived from a study of asset behaviour over a period of time. One such depreciation method is the depreciation method. Learn more about this method.

According to the depreciation method, depreciation is charged at a fixed percentage of the book value of the asset. It is also known as depreciation or depreciation because its book value decreases each year.

Since the book value decreases every year, the depreciation amount also decreases every year. This way, the value of the asset never goes to zero.

If you plot the depreciation amount billed this way and the corresponding period on the graph, the line will move down.

This method was previously based on the assumption that the cost of repairing an asset is low and therefore more depreciation costs must be charged. In addition, depreciation costs will decrease as repair costs increase in later years. Therefore, this method puts an equal burden on profits each year for the life of the asset.

However, this method may not provide full depreciation at the end of the asset's useful life if the applicable depreciation rate is not appropriate.

In addition, when applying this method, it is necessary to consider the period of use of the asset. If the asset is used for only two months in a year, depreciation will only be charged for two months.

However, if the asset is used for more than 180 days for income tax purposes, you will be charged full-year depreciation. Income tax rules also allow you to depreciate using the depreciation method.

The formula is:

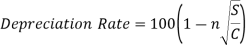
Where n=number of years

S=Salvage value

C=Cost of asset

Amount of depreciation=Book Value x Rate of Depreciation

100

SOYD method

Sum of the year method (SOYD)

Another accelerated depreciation method is the total number of years method. This method accelerates and recognizes depreciation. Therefore, the depreciation of an asset is billed fractionally over various accounting periods in this way.

This percentage is the ratio of the remaining useful life of the asset to the sum of the digits of the year for a particular period. Therefore, this percentage indicates that the profits from blocked capital or assets are highest in the first year.

Therefore, as an asset approaches the end of its useful life, the profits from such an asset diminish. That is, the most depreciation is allocated in the first year because the capital has not been recovered until then. Therefore, depreciation costs should be kept to a minimum last year as most of the invested capital has been recovered.

Year total digit depreciation formula

The following is the formula for the total number of years method.

Depreciation = Depreciation x (total useful life / years of the asset)

Where depreciation = asset costs – salvage value

Total year digits = (n (n + 1)) / 2 (where n = useful life of the asset)

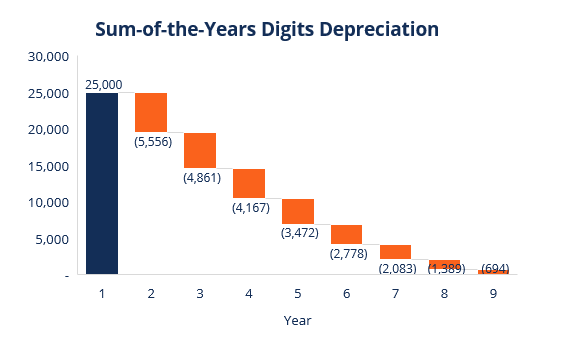
Example

Consider a device that costs $ 25,000, has an estimated useful life of eight years, and has a salvage value of $ 0. To calculate the total depreciation for years, set the following schedule:

The schedule information is as follows.

The depreciation standard is constant throughout the year and is calculated as follows:

Depreciation Criteria = Cost – Residual Value

Depreciation Criteria = $ 25,000 – $ 0 = $ 25,000

2. Remaining life is simply the remaining life of the asset. For example, assets at the beginning of the year have a remaining maturity of eight years. The following year, the remaining term of the asset is 7 years and so on.

3. RL / SYD is "remaining life divided by year total". In this example, the asset has a useful life of 8 years. Therefore, the sum of the years is 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 years. The remaining lifespan at the beginning of the first year is 8. Therefore, RM / SYD = 8/36 = 0.2222.

4. Multiply the RL / SYD number by the depreciation standard to determine the cost for the year.

5. The same will happen next year. At the beginning of the second year, RL / SYD will be 7/36 = 0.1944. 0.1944 x $ 25,000 = The cost for the second year is $ 4,861.

After tax comparison of projects

After-tax contributions are monetary contributions to the retirement plan after deducting taxes from the taxable income of an individual or company.

Post-tax contribution

Post-tax contributions are very popular with investments because the taxes have already been paid and the withdrawals made after retirement can be exempt. Understanding the whole post-tax contribution process are often very difficult because it requires an honest knowledge of the taxation process.

Basics of Contribution: Before and After Tax

In general, contributions to retirement plans can be made in two pre-tax and post-tax scenarios. As mentioned earlier, after-tax contributions are more popular with investors because they prefer not to pay taxes on withdrawals made from plans at a later date. After-tax contributions may be more profitable if the tax rate rises in the future.

Pre-tax contributions (previously made without paying taxes), unlike post-tax contributions, mean that an individual or company must pay taxes when withdrawing an amount from the retirement plan. Increase.

How does the post-tax contribution work?

The retirement plan, which uses after-tax contributions, consists of two main items. The original after-tax contributions made by the individual and the tax deferred income from the contributions. If a private withdraws money from the plan, the after-tax contribution isn't taxed, but the tax deferred income is taxed at the time of withdrawal.

In the United States, there are two main types of programs for after-tax contributions. Traditional after-tax contributions and Roth 401 (k) after-tax contributions.

Pros and cons of post-tax contribution

One of the most benefits of post-tax contributions is that individuals need to pay taxes on their contributions once they withdraw from the pension plan after retirement, as against pre-tax contributions that are taxed later. There is no such thing.

One of the main drawbacks of post-tax contributions is that the funds are divided into different components, making it much more difficult to figure out how much tax you have to pay.

On the opposite hand, if you made only pre-tax contributions within the past, it might be much easier because it might be easier to calculate the taxable amount.

Key takeaways:

1. In accounting terms, depreciation is defined as a systematic way to reduce the recorded cost of a fixed asset until the value of the asset becomes zero or negligible.
2. Depreciation is a gradual and continuous process because the value of an asset decreases due to the use of the asset or the expiration of time.
3. The actual cost or acquisition cost means the acquisition cost of the asset and includes all incidental costs required to return the asset to its current state and location.
4. The salvage value or scrap value is the expected value that may be realized when an asset is sold or exchanged at the end of its estimated useful life.
5. In accordance with the applicability of accounting standards to companies, companies must comply with the provisions contained in the standards.
6. The straight-line method is the default method used to evenly recognize the carrying amount of fixed assets over their useful lives.
7. Depreciation balance method was previously based on the assumption that the cost of repairing an asset is low and therefore more depreciation costs must be charged.
8. Another accelerated depreciation method is the total number of years method. This method accelerates and recognizes depreciation. Therefore, the depreciation of an asset is billed fractionally over various accounting periods in this way.
9. After-tax contributions are monetary contributions to the retirement plan after deducting taxes from the taxable income of an individual or company.
10. Pre-tax contributions (previously made without paying taxes), unlike post-tax contributions, mean that an individual or company must pay taxes when withdrawing an amount from the retirement plan.

References:

1. Https://www.economicsdiscussion.net/financial-management/time-value-of-money/32809
2. Https://www.engineeringtoolbox.com/cash-flow-diagrams-d_1231.html
3. Http://6thsemstuff.weebly.com/uploads/2/6/9/3/26934109/ee_lecture_no_05.pdf
4. Https://brainkart.com/article/Present-worth-method_5325/
5. Https://pestleanalysis.com/cost-benefit-analysis/
6. Https://corporatefinanceinstitute.com/resources/knowledge/other/after-tax-contribution/
7. Https://www.toppers4u.com/2020/10/need-causes-methods-of-depreciation.html