UNIT 2
The phase rule
Gibbs free energy: Gibbs free energy of the system is the difference of enthalpy of the system with the product of temperature times the entropy of the system.
G=H-TS
Gibbs free energy of the system is defined in term of the thermodynamics which are state in function. Any change in the Gibbs Free Energy System is directly proportional to the difference of change in the enthalpy of the system with the products of temperature times the entropy of the system.
G= H- (TS)
While at constant temperature this reaction transform into:
G= H-T S
The Nernst Equation is derived from the Gibbs free energy under standard conditions.
E*=E*reduction-E*oxidation ………..(i)
G=-nFE ………..(ii)
Where,
n=no. of transferred electrons in the reaction
F= Faraday constant
E=Potential Difference.
While when we see in the standard condition then, equation (ii) becomes
G*=-nFE* ………….(iii)
Hence,
Reaction is Spontaneous when E* is positive while non- spontaneous in vice-versa.
G= G*+RT lnQ ………….(iv)
Now, Substituting G=−nFE and G*=−nFE* into Equation 4, we have:
−nFE=−nFEo+RTlnQ …………….(v)
On Dividing both sides of the Equation above by −nF,
E=E*−RTnFlnQ(6) ……….(vi)
Equation (vi) in the form of log10:
E=E*−2.303RT/nF log10Q …….(vii)
At standard temperature T = 298 K, the 2.303RT/F term equals 0.0592 V and Equation
(vii) can be rewritten:
E=E*−0.0592V/n log10Q ……..(viii)
The equation (viii) clearly indicates that electric potential of cell depends on reaction quotient of reaction. The product formation leads to the increase in the concentration of the products. This tends to decrease the the potential of the cell until it reaches at the stage of equilibrium where, G=0 and G=-nFE Q=K so E=0
Then on substituting the these values to Nernst Equation we get,
0=E*-RT/nF In K …….(ix)
At room temperature it becomes;
0=E*-0.0592V/n Log10K
Log K=nE*/0.0592V
The above equation clearly indicates the equilibrium constant K is proportional to the standard potential.
Applications:
1- This is used in the solubility product and potentio-metric titration.
2- It is used to calculate the potential of ion charge.
3- It is used in oxygen and aquatic environment.
Water
The homogenous and physical part of the system is bounded by any surface which is mechanically separable is termed as phase. The phase may be the in the gaseous form, solid form or liquid form. The boundary present between the two interfaces is called as the interface. Air constitutes a single phase only as it contains a mixture of nitrogen, oxygen, carbon dioxide, water vapour etc. A system consisting of only one phase is said to be homogeneous. A mixture of two immiscible liquids such as water and benzene, will exist in two distinct liquid phases and in addition there will be a vapour phase. Thus there will be three phases each separated from the other by a well-defined bounding surface while the system consist of more than one phase is called as the heterogenous phase.
Phase Rule: If the equilibrium between any number of phases is not influenced by gravity, or electrical by surface action but are influenced only by temperature, pressure and concentration , then the number of degrees of freedom (F) of the system is related to the number of components (C ) and number of phases (P) by the following phase rule equation:
F=C-P+2
Liquid Phase:
(i) Liquid phase is depend on the number of liquids present and their missibility.
(ii) 2 miscible liquids form 2 separate liquid phase.
(iii) 2 miscible liquids form 1 liquid phase only.
Solid Phase:
Each solid forms a separate phase while number of solid phase depends on the number of solids present in it.
Gaseous Phase:
Due to the thoroughly miscible proportions of gases they form phases only.
Eg.: N2 and H2 mixture form phases only.
Applications to water system: In water there is only one component i.e., water and its phases: ice, water, steam that is solid, liquid and gaseous form. 
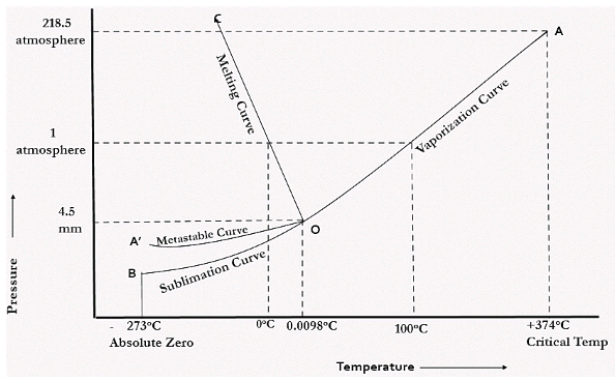
In the figure given above, the horizontal movement leads to be responsible for temperature change while the vertical curve responsible for the pressure change. In the above figure there are three curves i.e., OA,OB,OC which represents the equilibrium conditions between two phases solid with vapour, vapour with liquid and liquid with solid phase of water. Curve OC represents the equilibrium between solid and liquid phase of water. The curve is known as the fusion pressure or melting point curve. Along this curve there are two phases in equilibrium that is ice and water. At atmospheric pressure ice and water can be in equilibrium only at one temperature i.e, the freezing point of the water.
Here, C=1,
P=2
F=C-P+2
=1
Curve OB represent the equilibrium between liquid and vapor. This is called as the vaporization curve. Here also it is necessary to state either temperature or pressure. Eg.: at atmospheric pressure water and vapor can exists in equilibrium only at 1 temperature i.e., the boiling point of the water. Water vapor has also one degree of freedom.
F=C-P+2
=1
In some systems, equilibrium exists between solid - liquid phases and gaseous phase is practically absent. Hence the effect of pressure on such system can be neglected. Then it is necessary to take into account only two variables i.e.; temperature and concentration. Such system showing solid-liquid equilibrium is called condensed system and phase rule applied to such systems is as follows:
F = C – P + 1
Lead silver system- This system has two component and four phases. These are
But the boiling point of Ag and Pb is completely high; the vapor phase is completely absent.Since the press has nearly no affected on equilibrium so the system can be conveniently represented by temp.-conc. diagram.
Such solid liquid system with the gas phase is absent is called condensed system.
The experimental measurements of temp and conc. in condensed system ate usually carried at under atmosphere pressure.
Since the degree of freedom in such system is reduced but one, therefore, it can be also termed as reduced phase and represented by the equation,
F=C−P+1F=C−P+1
It is more convenient to apply to solid liquid two components condensed system e.g.-Pb-Sb, Ag-Pb, Zn-Cd
The complete temp.-conc. phase diagram of system silver-lead:
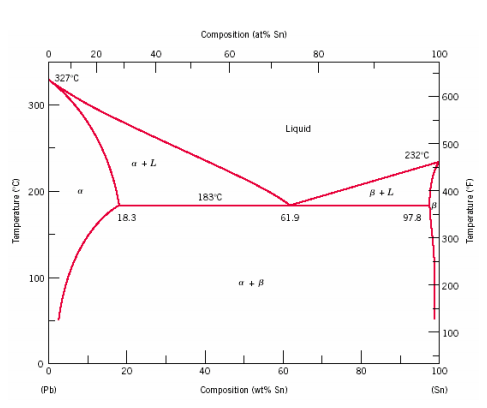
From the figure following salient features are observed:
- Curve AO →→Freezing curve of Hg.
i. It shows the effect on freezing point of Ag on addition of Pb in small quantities .
ii. The curve starts from (961)∘c(961)∘c the M.P of Ag, where pure Ag coexists as solid and liquid(Vapors being neglected)
iii. The curve indicates that the meeting point of Ag falls gradually on adding Pb, along AO till the lowest point O(303)∘c(303)∘c is reached where solution gets saturated with request to lead. At O more Pb can go in solution and consequently, the M.P. does not fall any further and if any Pb is added it separates as solid phase.
Along this curve, solid Ag and solution (Vapors being negligible) coexist and hence, according to reduced phase rule equation F=2−P+1F=2−P+1
i.e. system is invariant. The point O(303)∘c(303)∘c corresponds to a fixed composition of 2.62.6Ag and solution and 97.497.4 Pb and is known as eutectic composition.
On cooling the whole mass crystallizes out as such.
i. It represents the effect on freezing point of Pb on gradual addition of small amount of Ag to it, point B is the M.P of pure Pb(−327)∘c(−327)∘c
ii. Along BO, the M.P gradually falls on addition of Ag till lowest point O is reached
iii. At this point solution gets saturated with respect to Ag and M.P of Pb does not fall any more. List item
iv. On cooling whole mass crystallizes out. Therefore the system is univariant like AO.
3) Point O→Eutectic point Point O→Eutectic point_
The two curve AO and BO meet at O, where three phases solid Ag, solid Pb and their solution coexist and according phase rule. The point of O represents a fixed composition of Ag −2.6−2.6 is called eutectic composition.
At eutectic composition ^ temperature remains constant until the whole of melt solidifies in block to become solid of eutectic composition. However, further cooling results in simultaneous crystallization of a mixture of Ag and Pb in relative amounts corresponding to eutectic point O.
Bellow temperature line there are two regions.
Eutectic solid+solid Ag in crystalline -stable
Eutectic + solid Pb in crystalline-stable.
It represents solution of Pb-Ag sample of Pb containing less than 2.6% Ag is taken at an arbitrary pt. on curve allowing mass cool temp gradually falls without any charge in composition till this point is reached to curve BO(pt may be P).
On lowering the temp lead begins to separate out of the composition varies along Pb till pt 0 is reached.On cooling whole mass solidifies into a block.
Bismuth-Cadmium (Bi-Cd) is a prototype of a quasi-regular eutectic alloy in which the bismuth- rich phase has a volume fraction of 57%. Liquid metal such as Bi and Pb and Lead-Bismuth (Pb-Bi) eutectic alloy are serious contenders for use as coolant in the liquid metal-cooled fast breeder nuclear reactors (LMFBRs) in lieu of sodium due to a number of attractive characteristics (high density, low moderation, low neutron absorption and activation, high boiling point and poor interaction with water and air.). Lead-Bismuth eutectic is known to expand after solidification over time, up to about 1% volumetric. Cadmium-Lead (Cd-Pb) is a prototype of a regular eutectic alloy. These alloys were grown by Zone Refining Technique. The properties of alloys may vary according to phase diagrams. The alloys containing finer grains are hard and have high yield strength and ultimate strength. Their thermal and electric conductivities are low. An alloy containing coarse grains or large grains has low hardness, yield strength, ultimate strength and high values of thermal and electrical conductivities.
Isomorphous System
Isomorphous binary phase diagrams are found in a number of metallic and ceramic systems. In the isomorphous systems, only one solid phase forms; the two components in the system display complete solid solubility. Typically, the isomorphous system has a liquid area, a solid area, and an area that is a mixture of both liquid and solid. Typically, a binary isomorphous phase diagram consists of two phase boundaries: the liquidus and the solidus.
