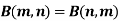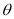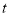Module -1

Partial differentiation

1.1           Asymptote

A straight line on a graph that represents a limit for a given function. Imagine a curve that comes closer and closer to a line without actually crossing it.

1.2           Curvature (Cartesian and polar)

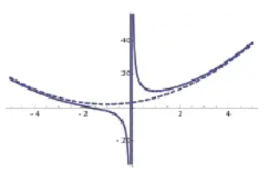
r = cos(θ) + sin(θ)

This curve has Cartesian equation

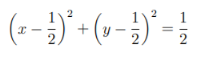
The curve is a circle.

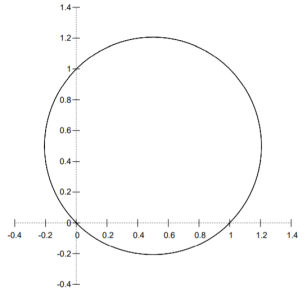
r = cos(θ) + sec(θ)

This curve has Cartesian equation x3 + xy2 − 2x2 − y2 = 0 and asymptote x = 1.

1.3           Gamma & Beta function

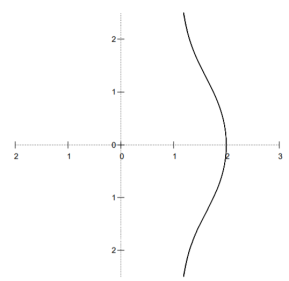
Ex.1: Evaluate   0∞  x3/2  e -x dx

Solution:               0∞  x3/2  e -x dx          =   0∞  x 5/2-1  e -x dx  

=  γ(5/2)

=   γ(3/2+ 1) 

=    3/2   γ(3/2 )  

=   3/2 .  ½   γ(½ ) 

=  3/2 . ½ .π 

=    ¾ π  

Ex. 2: Find  γ(-½) 

Solution:       (-½) + 1  =  ½
γ(-1/2)  =   γ(-½ + 1)  / (-½)   

=   - 2   γ(1/2 )  

=  - 2 π  

Ex. 3.  Show that      

Solution : =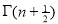

=

= )  .......................

=

=

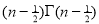
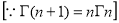
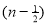
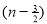
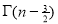
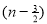
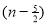
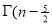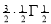
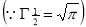
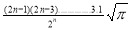
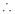
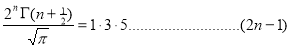
Ex. 4: Evaluate  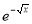dx.

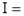
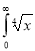
Solution :  Let   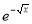 dx 

X	0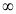
t	0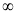

Put 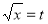or 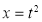;dx =2t 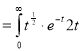dt .

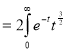dt

dt

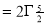
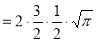
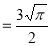
Ex. 5: Evaluate 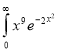  dx.

Solution :   Let 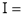 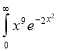 dx.

x	0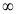
t	0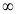

Put 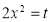or 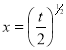 ;             4x dx = dt

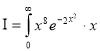dx

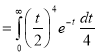
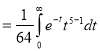
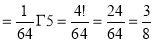
Definition : Beta function

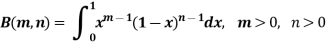
Properties of Beta function :

2.

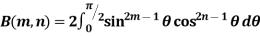3.

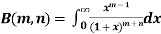4.

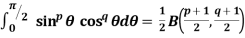Example(1):  Evaluate    I   =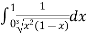  

Solution: 

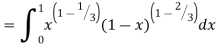
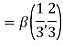
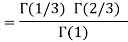
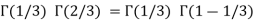
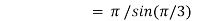
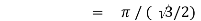
= 2 π/3

Example(2): Evaluate:  I =  02  x2   / (2 – x )   . Dx

Solution:

Letting   x  = 2y, we get

I   =   (8/2) 01  y 2  (1 – y ) -1/2dy

=  (8/2) . B(3 , 1/2 )

= 642 /15 

BETA FUNCTION MORE PROBLEMS

Relation between Beta and Gamma functions :

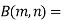Example(1):   Evaluate:  I =  0a  x4   (a2 – x2 )   . Dx Solution:                      Letting   x2  = a2 y , we get I   =   (a6  / 2) 01  y 3/2  (1 – y )1/2dy =  (a6  / 2) .  B(5/2 , 3/2 ) =  a6  /3 2 Example(2):   Evaluate:  I =  02 x (8 – x3 )   . Dx Solution:                Let   x3  = 8y I =  (8/3) 01  y-1/3      (1 – y ) 1/3   . Dy   = (8/3) B(2/3 , 4/3 ) =  16 π / ( 9 3 )   Example(3):   Prove that 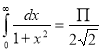Solution : Let 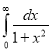Put  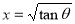 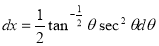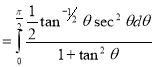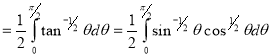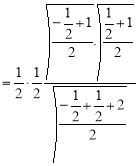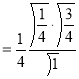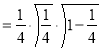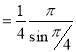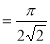or  ,  Example(4):  Evaluate 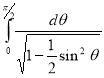Solution :Let 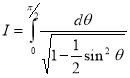Put  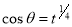 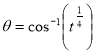or  , , When 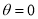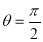, ; , o 1 0 Also  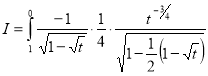 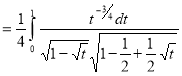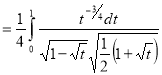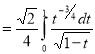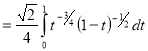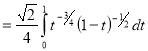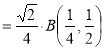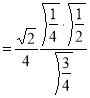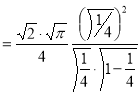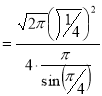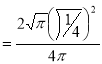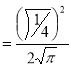Example(5):   Show that Solution : 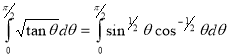= 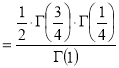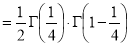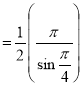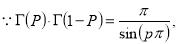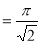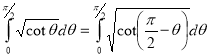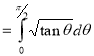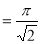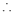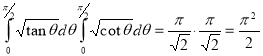( 0<p<1) (by above result)   Exercise : - Q. Show that 1. 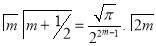 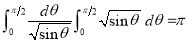 2.

1.4           Partial differentiation

Partial Differentiation

If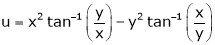

Prove that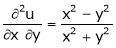

Partial differentiation of function of function

If z = f(u) and 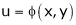. Then z becomes a function of x & y. In this case z becomes a function of function of x & y.

i.e.

Then

,

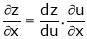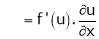
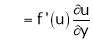
Similarly

If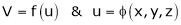

Then z becomes a function of function of x, y & z.

…………….

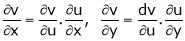
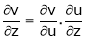1. If 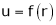where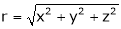

Prove that

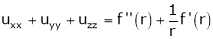
2.     If V = 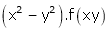show that

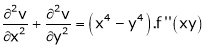
3.     If 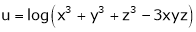show that

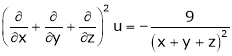
4.     If 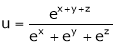then prove that

1.5 Maxima and Minima for function of two variables

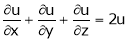
Let z = f(x, y)

Now for stationary point dz = 0

&

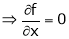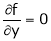
This gives the set of values of x and y for which maxima or minim occurs

Now find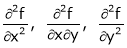

We called it as r, s, t resp.

Thus function has maximum or minimum

If rt – s2 >0

i.e.

Further if

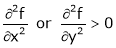1. ; function is minimum at (x, y) &
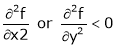2. ; Function is maximum at (x, y)

Note that

1. If 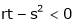; then function will not have either maxima or minima such point is called saddle point.
2. If ; then more details are required to justly maxima or minima

Ex. Discuss the stationary values of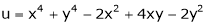

Ex. Find the values of x and y for which x2 + y2 + 6x = 12 has a minimum values and find its minimum value.

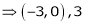
Divide 120 into three parts so that the sum of their product. Taken two at a times shall be maximum.

Using Lagrange’s method divide 24 into three parts. Such that continued product of the first, square of second, cube of third may be maximum.

Find the maximum and minimum value of x2 + y2 when 3x2 + 4xy + 6y2 = 140

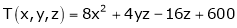
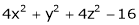is satisfied.

References

1. Ordinary and Partial Differential equations by J. Sihna Ray and S Padhy, Kalyani Publishers

2. Advance Engineering Mathematics by P.V.O’NEIL, CENGAGE

3. Ordinary Differential Equation by P C Biswal , PHI secondedition.

4. Engineering Mathematics by P. S. Das & C. Vijayakumari, Pearson. N.B:Thecourseisof3creditwith4contacthours.