Unit – 4
Differential equations
The general form of linear differential equation of second order is
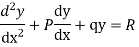
Where p and q are constants and R is a function of x or constant.
Differential Operator
D stands for operation of differential i.e.
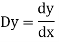
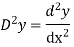
stands for the operator of integration.
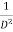stands for operation of integration twice.
Thus,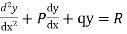 
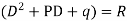
Note:- Complete solution = complementary function + Particular integral
i.e. y=CF + PI
Method for finding the CF
Step1:- In finding the CF right hand side of the given equation is replaced by zero.
Step 2:- Let 
be the CF of
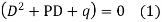
Putting the value of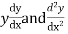 
in equation (1) we get
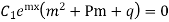
It is called auxiliary equation.
Step 3:- Roots Real and Different
If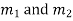 
are the roots the CF is 
If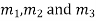 
are the roots then 
Step 4- Roots Real and Equal
If both the roots are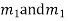 
then CF is
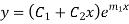
If roots are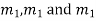 
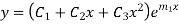
Example: Solve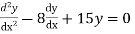 
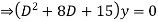
Ans. Given,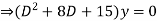 
Here Auxiliary equation is
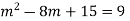
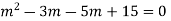
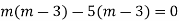
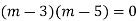
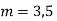
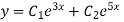
Solve: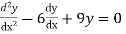 
Or,
Ans. Auxiliary equation are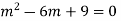 
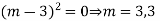
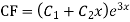
Note: If roots are in complex form i.e.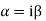 
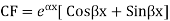
Solve: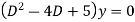 
Ans. Auxiliary equation are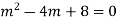 
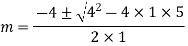
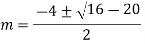
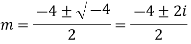
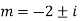
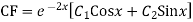
Solve. 
Ans. Its auxiliary equation is
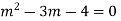
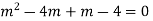
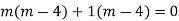
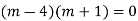
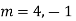
Solution is 
Solve. 
Ans. The auxiliary equation is
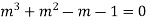
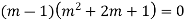
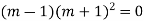
Hence the solution is
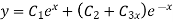
Rules to find Particular Integral
Case 1: 
If,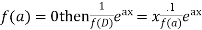 
If,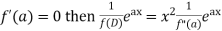 
Solve: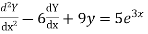 
Ans. Given,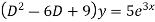 
Auxiliary equation is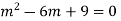 
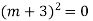
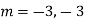
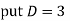
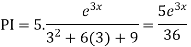
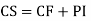
Case2: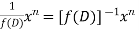 
Expand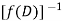 
by the binomial theorem in ascending powers of D as far as the result of operation on 
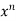is zero.
Solve.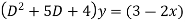 
Given,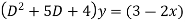 
For CF,
Auxiliary equation are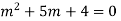 
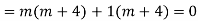
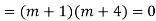
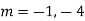
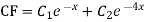
For PI
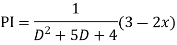
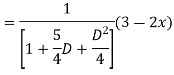
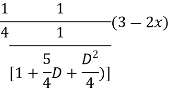
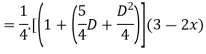
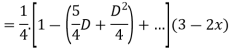
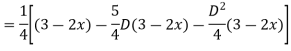
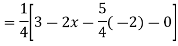
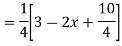
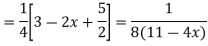
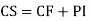
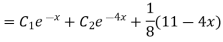
Case 3: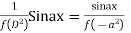 
Or,
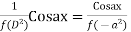
Solve: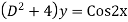 
Ans. Auxiliary equation are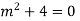 
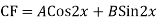
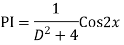
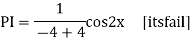
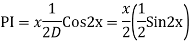
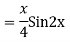
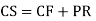
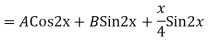
Case 4: 
Solve.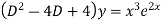 
Ans. AE=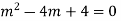 
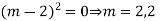
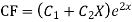
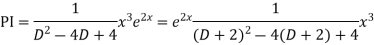
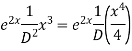
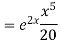
Complete solution is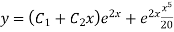 
Solve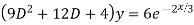 
Ans. The AE is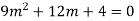 
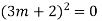
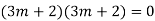
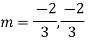
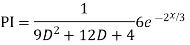
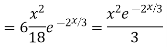
Complete solution y= CF + PI
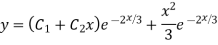
Solve.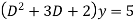 
Ans. The AE is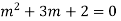 
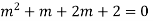
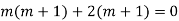
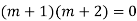
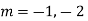
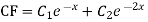
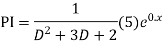
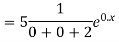
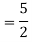
Complete solution = CF + PI
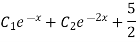
Solve.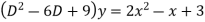 
Ans. The AE is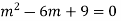 
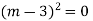
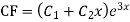
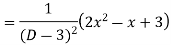
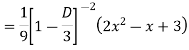
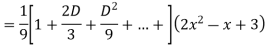
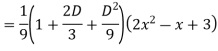
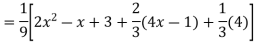
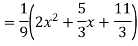
Complete solutio0n is y= CF + PI
Find the PI of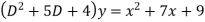 
Ans. 
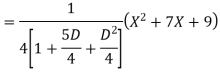
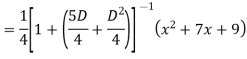
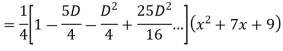
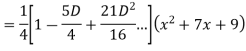
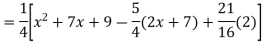
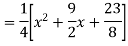
Solve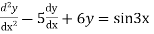 
Ans. Given equation in symbolic form is
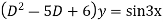
Its Auxiliary equation is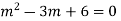 
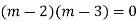
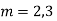
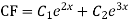
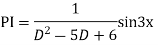
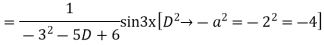
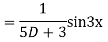
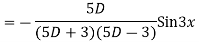
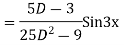
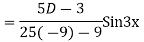
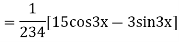
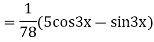
Complete solution is y= CF + PI
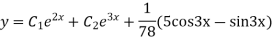
Solve.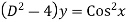 
Ans. The AE is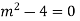 
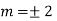
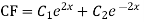
We know,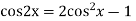 
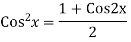
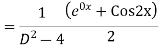
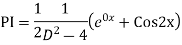
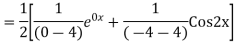
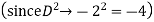
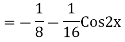
Complete solution is y= CF + PI
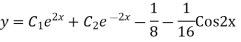
Solve. Find the PI of (D2-4D+3)y=ex cos2x
Ans.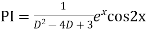 
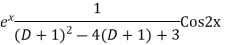
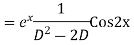
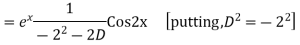
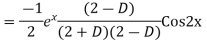
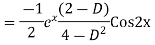
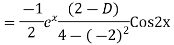
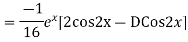
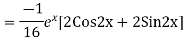
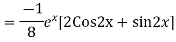
Solve. (D3-7D-6) y=e2x (1+x)
Ans. The auxiliary equation i9s
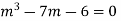
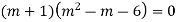
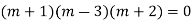
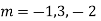
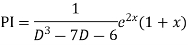
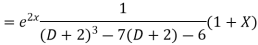
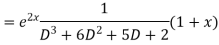
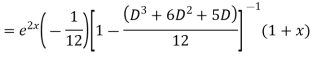
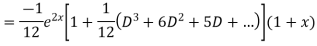
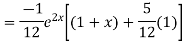
Hence complete solution is y= CF + PI
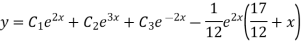
Working Rule
Step 1 Let 
be the solution of the given differential equation.
Step 2: Find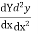 
etc.
Step 3: Substitute the expression of 
in the given differential equation.
Step 4: Calculate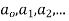 
coefficient of various powers of x by equating coefficients to zero.
Step 5: Substitute the values of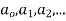 
in the differential equation to get the required series solution.
Example. Solve in series the equation
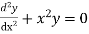
Ans. 
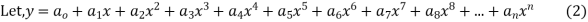
Since x=0 is the ordinary point of the equation (1)
Then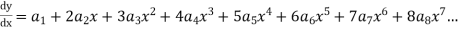 
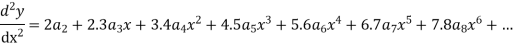
Substituting in (1) we get
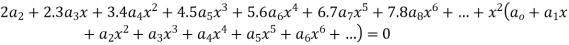
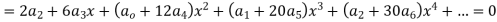
Equating to zero the coefficient of the various powers of x we obtain
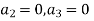
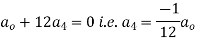
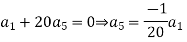
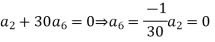
Substituting these values in (2) we get
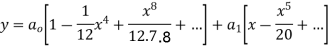
Solve.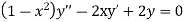 
Ans. Let,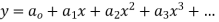 
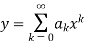
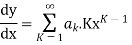
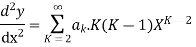
Substituting the value of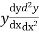 
in the given equation we get
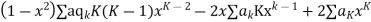
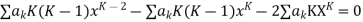
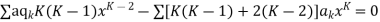
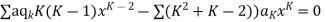
Where the first summation extends over all values of K from 2 to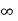 
And the second from K =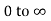
Now equating the coefficient of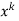 
equal to zero we have
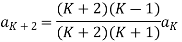
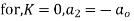
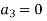
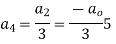
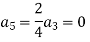
For K =4
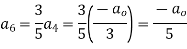
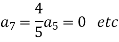
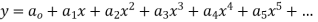
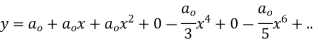
Solve.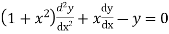 
Ans. Let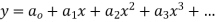 
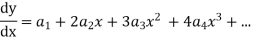
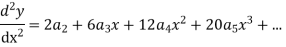
Substituting for 
in the given differential equation
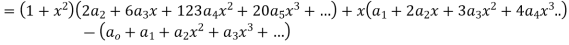
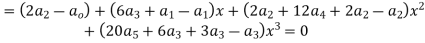
Equating the coefficients of various powers of x to zero we get
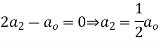
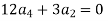
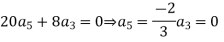
Legendre’s equation is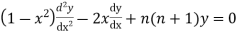 
And 
Prove that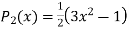 
Ans. We know that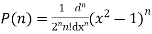 
Put n=2
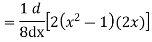
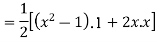
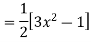
Prove that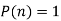 
.
Ans. We know
+
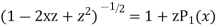Put x = 1 both sides we get
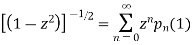
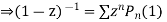
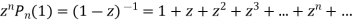
Equating the coefficient of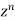 
on both sides we get
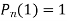
Prove that 
Ans. We know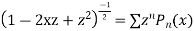 
Differentiating with respect to z we get
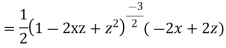
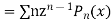
Multiplying both sides by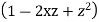 
we get
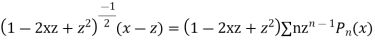
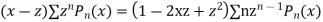
Equating the coefficient of 
from both sides we get
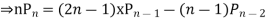
Solve. Statement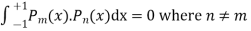 
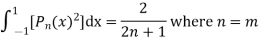
Proof. Let 
is a solution of
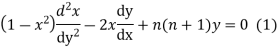
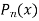is the solution of
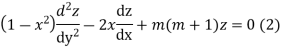
Multiplying (1) by z and (2) by y and subtracting we get
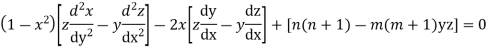
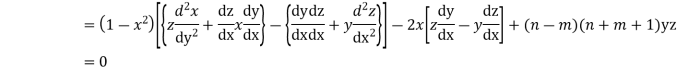
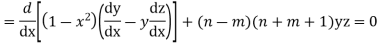
Now integrative -1 to 1 we get
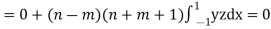
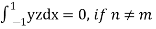
Now we have to prove that
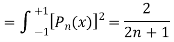
We know that,
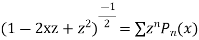
Squaring both sides we get
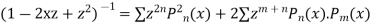
Integrating both sides between -1 to +1 we get
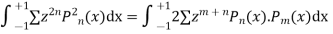
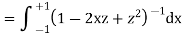
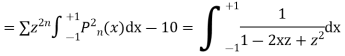
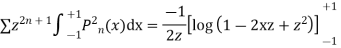
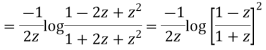
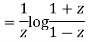
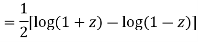
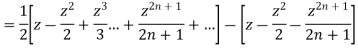
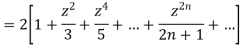
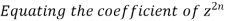on both sides we get
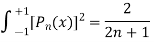
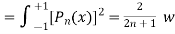here n = m
Prove that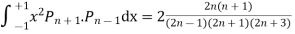 
Ans. The Recurrence formula is
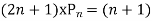Pn+1+nPn-1
Replacing n by (n+1) and (n-1) we have
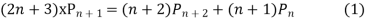
Multiplying (1) and (2) and integrating in the limits -1 to 1 we get
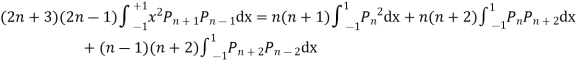
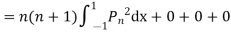(By orthogonality property)
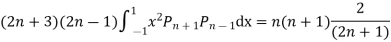
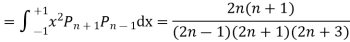
The Bessel equation is
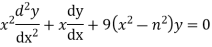
Bessel function of first kind
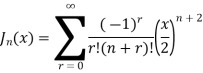
Bessel function of second kind
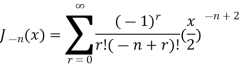
Recurrence Formula
1) xJn'=nJn-xJn+1
2) 
3) 
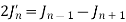
4) 
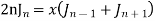
5) 
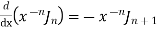
6) 
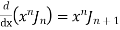
Prove that (1) 
Ans. We know
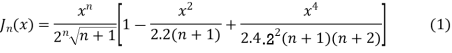
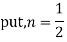
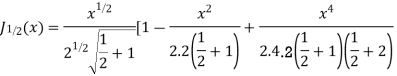
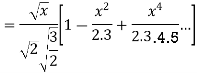
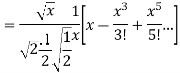
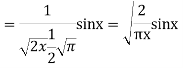
(b) Prove that 
Ans. We know that
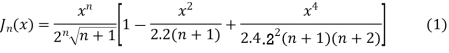
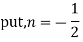
(3) Prove that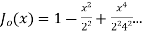 
Ans. We know that
Jn(x)=
If n = 0
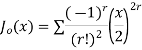
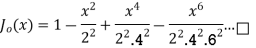
If n = 1
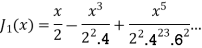
Note General solution of Bessel Equation
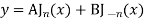
References
1. Ordinary and Partial Differential equations by J. Sihna Ray and S Padhy, Kalyani Publishers
2. Advance Engineering Mathematics by P.V.O’NEIL, CENGAGE
3. Ordinary Differential Equation by P C Biswal , PHI secondedition.
4. Engineering Mathematics by P. S. Das & C. Vijayakumari, Pearson. N.B:Thecourseisof3creditwith4contacthours.
