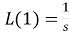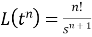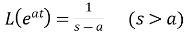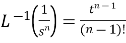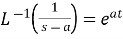Module – 5
Laplace transformation
Definition:Let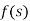 
be function defined for all positive values of t, then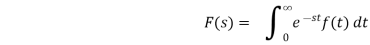 
Provided the integral exists, is called the Laplace Transform of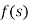 
. It is denoted as -
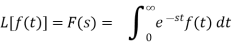
Important Formulae:
4. 
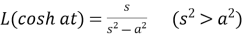
5. 
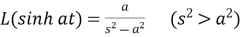
6. 
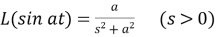
7. 
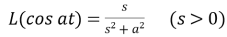
Example1. Find the Laplace transform of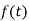 
defined as
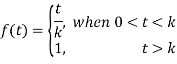
Solution:
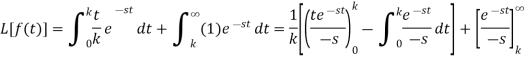
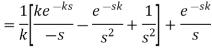
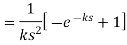
Example2. From the first principle, find the Laplace transform of (1 + cos 2 t)
Solution: Laplace transform of (1 + cos 2 t)
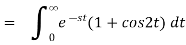
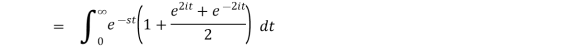
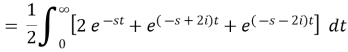
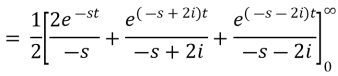
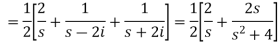
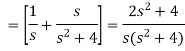
Example3. Find the Laplace transform of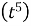
Solution:
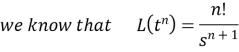
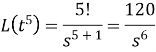
Now we obtain f (t) when F (s) is given, then we say that inverse Laplace transform of F (s) is f (t).
Where,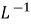
is called the inverse Laplace transform operator.
From the application point of view, the inverse Laplace transform is very useful.
IMPORTANT FORMULAE:
4. 
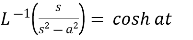
5. 
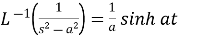
6. 
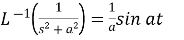
7. 
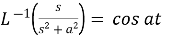
8. 
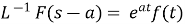
9. 
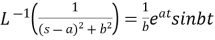
10.
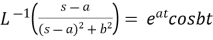
11.
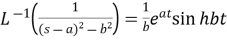
12.
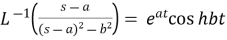
13.
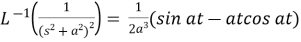
14.
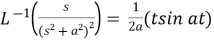
15.
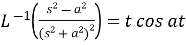
16.
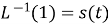
17.
MULTIPLICATION by s: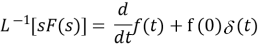 
DIVISION by s: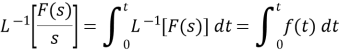
Example1: Find the inverse Laplace Transform of
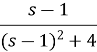
Solution: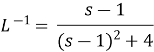
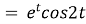
Example2: Find the inverse Laplace Transform of
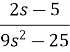
Solution: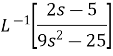
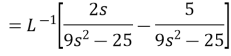
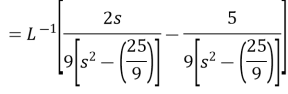
Example3: Find the inverse Laplace Transform of function by MULTIPLICATION by s
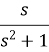
Solution:
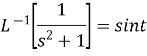
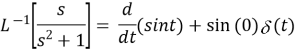
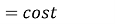
Example4: Find the inverse Laplace Transform of function by Division by s
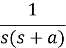
Solution:
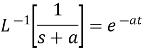
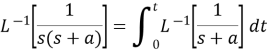
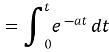
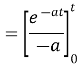
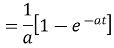
Example1: Evaluate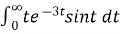 
Solution: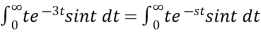 
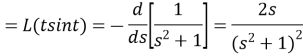
Example2: Evaluate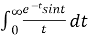 
Solution: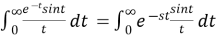 
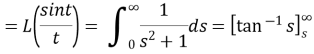
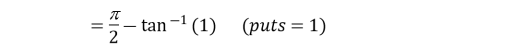
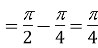
Example3: Evaluate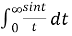 
Solution: 
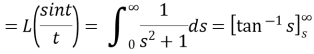
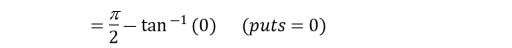
References
1. Ordinary and Partial Differential equations by J. Sihna Ray and S Padhy, Kalyani Publishers
2. Advance Engineering Mathematics by P.V.O’NEIL, CENGAGE
3. Ordinary Differential Equation by P C Biswal , PHI secondedition.
4. Engineering Mathematics by P. S. Das & C. Vijayakumari, Pearson. N.B:Thecourseisof3creditwith4contacthours.
