Unit - 3
Sinusoidal steady state analysis
Average Value:
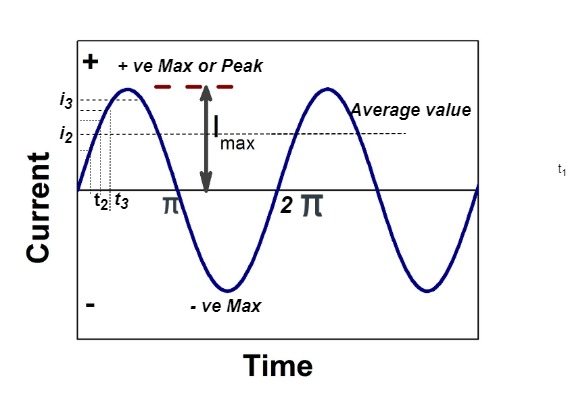
Fig. Sinusoidal waveform
The arithmetic means of all the value over complete one cycle is called as average value
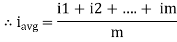
 =
= 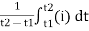
For the derivation we are considering only hall cycle.
Thus 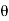 varies from 0 to ᴫ
varies from 0 to ᴫ
i = Im Sin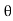
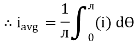
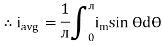
Solving
We get
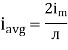
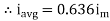
Similarly, Vavg=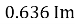
The average value of sinusoid ally varying alternating current is 0.636 times maximum value of alternating current.
RMS value: Root mean square value
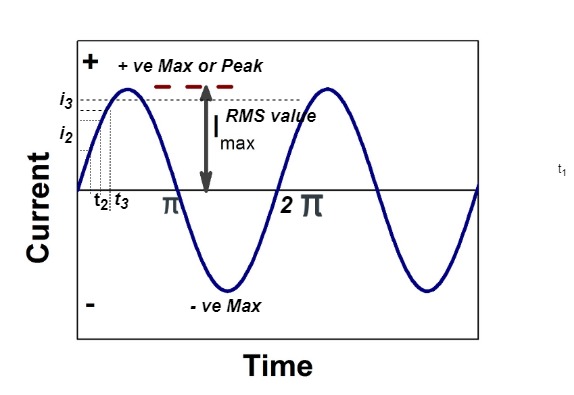
Fig. Sinusoidal waveform
The RMS value of AC current is equal to the steady state DC current that required to produce the same amount of heat produced by ac current provided that resistance and time for which these currents flows are identical.
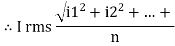
I rms = 
Direction for RMS value:
Instantaneous current equation is given by
i = Im Sin 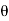
but 
I rms = 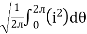
= 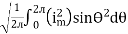
=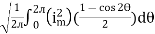
=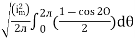
Solving
=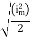
=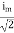
Similar we can derive
V rms=  or 0.707 Vm
or 0.707 Vm
 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
The alternating quantities (voltages and currents) in practice are represented by straight lines having definite direction and length. Such lines are called the phasors and the diagrams in which phasors represent currents, voltages and their phase difference are known as phasor diagrams.
Though phasor diagrams can be drawn to represent either maximum or effective values of voltages and currents but since effective values are of much more importance, phasor diagrams are mostly drawn to represent effective values.
In order to achieve consistent and accurate results it is essential to follow certain conventions.
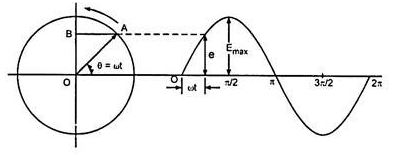
Fig. Phasor Diagram
The above figure shows that OA is the maximum ac quantity present. The OA represents emf on vertical axis. This phasor of OA in ACW direction represents sinusoidal voltage or current. Its angular velocity is one revolution complete in same time as by the alternating voltage or current.
The ACW is taken positive for phasor. In series circuit current phasor is taken as reference as the current is same. In parallel circuit voltage is taken as reference as it is same throughout.
Impedances
The ac circuit is to always pure R pure L and pure C it well attains the combination of these elements. “The combination of R1 XL and XC is defined and called as impedance represented as
Z = R +i X
Ø = 0
 only magnitude
only magnitude
R = Resistance, i = denoted complex variable, X =Reactance XL or Xc
Polar Form
Z = 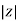 L I
L I
Where 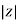 =
=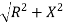
 Measured in ohm
Measured in ohm
Admittances
The reciprocal of impedance is admittance. Its unit is mho (siemens)
Y=  =
= 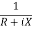
V=IZ
I=VY
Y= 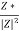 =
= 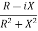
Y= G+iB
G= 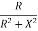
B= 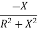
Ac circuit containing pure resisting
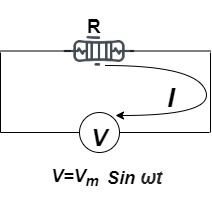
Consider Circuit Consisting pure resistance connected across ac voltage source
V = Vm Sin ωt ①
According to ohm’s law i =  =
= 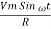
But Im = 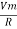
 ②
②
Phase’s diagram
From ① and ②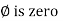 phase or represents RMD value.
phase or represents RMD value.
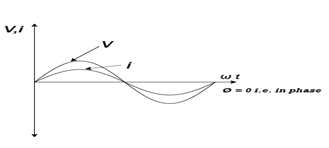
Fig. Phasor Diagram
Power P = V. i
Equation P = Vm sin ω t Im sin ω t
P = Vm Im Sin2 ω t
P = 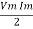 -
- 
Constant fluctuating power if we integrate it becomes zero
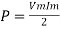
Average power
Pavg = 
Pavg = 
Pavg = Vrms Irms
Power form [Resultant]
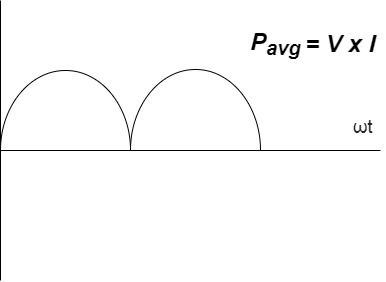
Fig. Resultant Power
Ac circuit containing pure Inductors
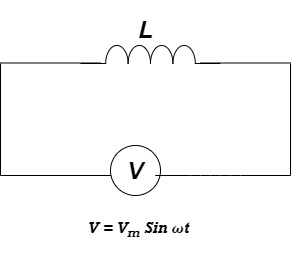
Fig. Inductive circuit
Consider pure Inductor (L) is connected across alternating voltage. Source
V = Vm Sin ωt
When an alternating current flow through inductance it set ups alternating magnetic flux around the inductor.
This changing the flux links the coil and self-induced emf is produced
According to faradays Law of E M I
e = 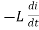
at all instant applied voltage V is equal and opposite to self-induced emf [ lenz’s law]
V = -e
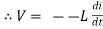 =
= 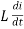
But V = Vm Sin ωt
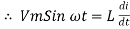
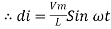 dt
dt
Taking integrating on both sides
 dt
dt
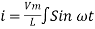 dt
dt
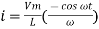
 (-cos
(-cos 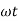 )
)
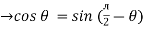
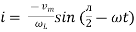
but sin (–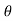 ) = sin (+
) = sin (+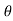 )
)
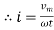 sin (
sin (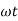 -
- 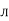 /2)
/2)
And Im= 
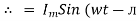 /2)
/2)
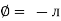 /2
/2
= -ve
= lagging
= I lag v by 900
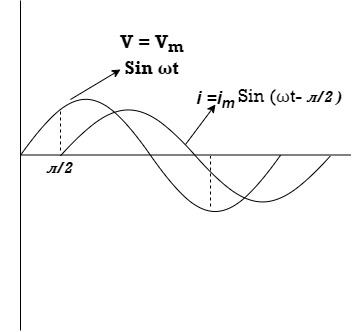
Fig. Voltage and Current waveform
Phasor:
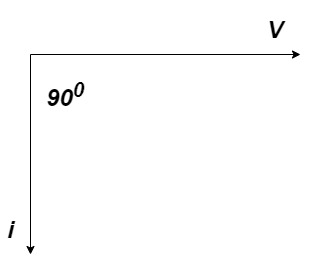
Fig. Phasor for L circuit
Power P = Ѵ. I
= Vm sin wt Im sin (wt  /2)
/2)
= Vm Im Sin wt Sin (wt –  /s)
/s)
 ①
①
And
Sin (wt - 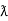 /s) = - cos wt ②
/s) = - cos wt ②
Sin (wt –  ) = - cos
) = - cos 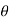
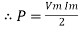 sin 2 wt from ① and ②
sin 2 wt from ① and ②
The average value of sin curve over a complete cycle is always zero
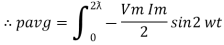
 Pavg = 0
Pavg = 0
Ac circuit containing pure capacitors:
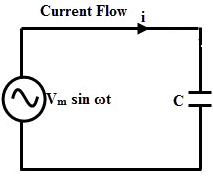
Fig. Pure Capacitive Circuit
Consider pure capacitor C is connected across alternating voltage source
Ѵ = Ѵm Sin wt
Current is passing through capacitor the instantaneous charge ɡ produced on the plate of capacitor
ɡ = C Ѵ
ɡ = c Vm sin wt
the current is rate of flow of charge
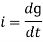
i= (cvm sin wt)
(cvm sin wt)
i = c Vm w cos wt
then rearranging the above eqn.
i =  cos wt
cos wt
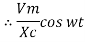
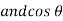 = sin (wt +
= sin (wt +  X/2)
X/2)
i = 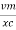 sin (wt + X/2)
sin (wt + X/2)
but 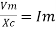
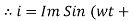 X/2)
X/2)
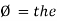
= leading
= I leads V by 900
Waveform:
Fig. V_I waveform
Phase
Fig. Phasor for C circuit
Power P= Ѵ. i
= [Vm sinwt] [ Im sin (wt + X/2)]
= Vm Im Sin wt Sin (wt + X/2)]
 (cos wt)
(cos wt)
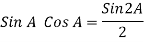
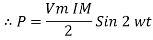
 to charging power waveform [resultant].
to charging power waveform [resultant].
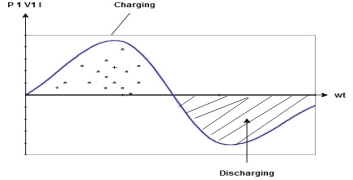
Fig. Power Waveform
RMS value: Root mean square value

The RMS value of AC current is equal to the steady state DC current that required to produce the same amount of heat produced by ac current provided that resistance and time for which these currents flows are identical.
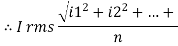
I rms = 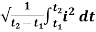
Direction for RMS value:
Instantaneous current equation is given by
i = Im Sin 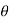
but 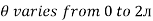
I rms = 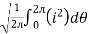
= 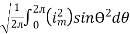
=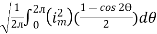
=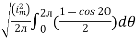
Solving
=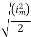
=
Similar we can derive
V rms= 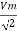 or 0.707 Vm
or 0.707 Vm
 the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
the RMS value of sinusoidally alternating current is 0.707 times the maximum value of alternating current.
Real Power: [P]
It is nothing but the actual power being used in a circuit.
P=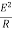 = I2R Watts
= I2R Watts
Reactive Power: [Q]
It is the function of reactance in the circuit X. Mainly reactive loads are inductor and capacitors. These elements dissipate zero power. These element shows that they dissipate power. This is called as reactive power.
Q=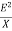 = I2X VAR (volt-Ampere-Reactive)
= I2X VAR (volt-Ampere-Reactive)
Apparent Power: [S]
It is the product of a circuit voltage and current without reference to phase angle. It is the combination of both reactive and real power.
S=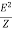 = I2Z VA (volt-Ampere)
= I2Z VA (volt-Ampere)
Power factor (P.F.)
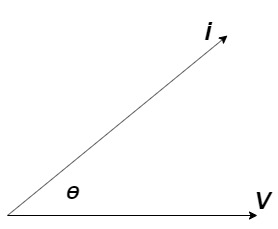
Fig. Power Factor
It is the cosine of angle between voltage and current
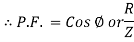
If Ɵ is –ve or lagging (I lags V) then lagging P.F.
If Ɵ is +ve or leading (I leads V) then leading P.F.
If Ɵ is 0 or in phase (I and V in phase) then unity P.F.
Examples
Que) A coil takes a current of 6A when connected to 24V dc supply. To obtain the same current with 50HZ ac, the voltage required was 30V. Calculate inductance and p.f of coil?
Sol: The coil will offer only resistance to dc voltage and impedance to ac voltage
R =24/6 = 4ohm
Z= 30/6 = 5ohm
XL = 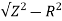
= 3ohm
cosφ =  = 4/5 = 0.8 lagging
= 4/5 = 0.8 lagging
Que) The potential difference measured across a coil is 4.5V, when it carries a dc current of 8A. The same coil when carries ac current of 8A at 25Hz, the potential difference is 24V. Find current and power when supplied by 50V,50Hz supply?
Sol: R=V/I= 4.5/8 = 0.56ohm
At 25Hz Z= V/I=24/8 =3ohm
XL = 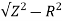
= 2.93ohm
XL = 2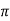 fL = 2
fL = 2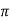 x 25x L = 2.93
x 25x L = 2.93
L=0.0187ohm
At 50Hz
XL = 2x3 =6ohm
Z = 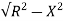 = 5.97ohm
= 5.97ohm
I= 50/5.97 = 8.37A
Power = I2R = 39.28W
Que) A coil having inductance of 50mH an resistance 10ohmis connected in series
with a 25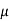 F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
F capacitor across a 200V ac supply. Calculate resonant frequency and current flowing at resonance?
Sol: f0= = 142.3Hz
= 142.3Hz
I0 = V/R = 200/10 = 20A
Que) A 15mH inductor is in series with a parallel combination of 80ohm resistor and 20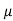 F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
F capacitor. If the angular frequency of the applied voltage is 1000rad/s find admittance?
Sol: XL = 2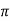 fL = 1000x15x10-3 = 15ohm
fL = 1000x15x10-3 = 15ohm
XL = 1/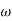 C = 50ohm
C = 50ohm
Impedance of parallel combination Z = 80||-j50 = 22.5-j36
Total impedance = j15+22.5-j36 = 22.5-j21
Admittance Y= 1/Z = 0.023-j0.022 siemens
Que) A circuit connected to a 100V, 50 Hz supply takes 0.8A at a p.f of 0.3 lagging. Calculate the resistance and inductance of the circuit when connected in series and parallel?
Sol: For series Z =100/0.8 = 125ohm
cosφ = 
R = 0.3 x 125 = 37.5ohm
XL = 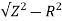 = 119.2ohm
= 119.2ohm
XL = 2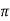 fL = 2
fL = 2 x 50x L
x 50x L
119.2 = 2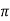 x 50x L
x 50x L
L= 0.38H
For parallel:
Active component of current = 0.8 cosφ = 0.3x0.3 = 0.24A
R = 100/0.24 =416.7ohm
Quadrature component of current = 0.8 sinφ = 0.763
XL= 100/0.763 = 131.06ohm
L= 100/0.763x2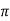 x50 = 0.417H
x50 = 0.417H
Que) For a series RLC circuit having R=10ohms, L= 0.15H, C=100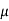 F. They are connected across 100v 50Hz supply. Calculate total impedance?
F. They are connected across 100v 50Hz supply. Calculate total impedance?
Sol: Impedance Z= 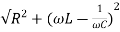
Z=  = 18.27ohm
= 18.27ohm
Que) For a series RLC circuit having R=12ohms, L= 0.2H, C=60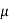 F. They are connected across 100v 50Hz supply. Calculate circuit current?
F. They are connected across 100v 50Hz supply. Calculate circuit current?
Sol: I= 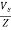
Z= 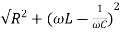
Z= 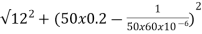 = 13.89ohm
= 13.89ohm
I = 100/13.89 =7.2A
Que) For a series RLC circuit having R=10ohms, L= 0.15H, C=100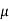 F. They are connected across 100v 50Hz supply. Calculate power factor?
F. They are connected across 100v 50Hz supply. Calculate power factor?
Sol: cosφ = 
Impedance Z= 
Z=  = 18.27ohm
= 18.27ohm
cosφ =  =
= 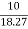
φ = 56.81o lagging
In three phase the windings are separated by 1200 each. The voltage produced in those windings are 1200 apart from each other. Below shown is one coil RR’ and two more coils YY’ and BB’ each having phase shift of 1200.

Fig. Three phase circuit waveform
The instantaneous value of voltages is given as
VRR’ = Vmsinωt
VYY’ = Vmsin(ωt-120)
VBB’ = Vmsin(ωt-240)
The three phase voltages are of same magnitude and frequency.
Phase sequence
The change in voltage is in order VRR’- VYY’- VBB’. So, the three-phase are changed in that order and are called as phase change.
VRR’ = Vmsinωt
VYY’ = Vmsin(ωt-120)
VBB’ = Vmsin(ωt-240)
MUTUAL INDUCTANCE: -

Fig. Mutual Inductance
M12= mutual inductance on 1 due to 2
M21= mutual inductance on 2 due to 1
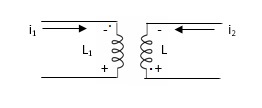
Fig. Current entering both dots
voltage on 2 due to 1 = 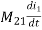
voltage on 1 due to 2 = 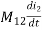
1. When current is entering or leaving from both dots.
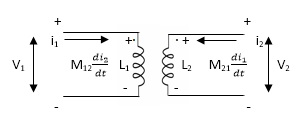
Fig. Current entering both dots
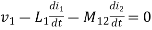 ⎼⎼⎼⎼⎼⎼ 1
⎼⎼⎼⎼⎼⎼ 1
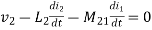 ⎼⎼⎼⎼⎼⎼2
⎼⎼⎼⎼⎼⎼2
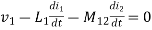 ⎼⎼⎼⎼⎼⎼⎼1
⎼⎼⎼⎼⎼⎼⎼1
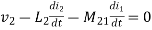 ⎼⎼⎼⎼⎼⎼⎼2
⎼⎼⎼⎼⎼⎼⎼2
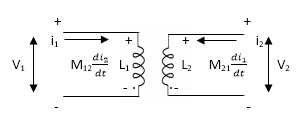
2. When current is entering from one dot and leaving the other
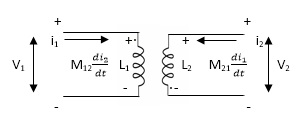
Fig. Current entering one dot and leaving other
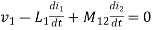 ⎼⎼⎼⎼⎼⎼⎼⎼1
⎼⎼⎼⎼⎼⎼⎼⎼1
 ⎼⎼⎼⎼⎼⎼⎼⎼2
⎼⎼⎼⎼⎼⎼⎼⎼2
3. When current is entering in both dots
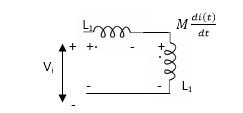
Find 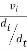 =?
=?
Fig. Current enters both dots
If M12= M21= M
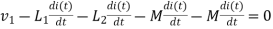
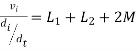
4. When current leaves both dots
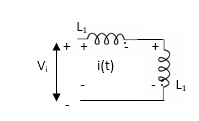
Find 
Fig. Current Leaving both dots
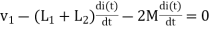
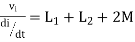
5. When current enters from L1 and leaves L2

Find 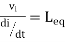
Fig. current enters from L1 and leaves L2

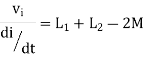
6. When current leaves L2and enters L1
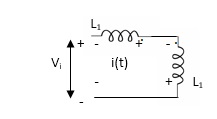
Fig. current leaves L2and enters L1
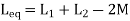
Key takeaway
The current entering the dot is taken as positive.
Example 1. Find 
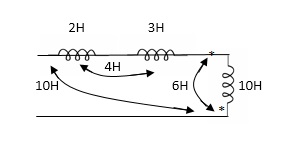
 = 2H + 3H +10H - 2(10H) + 2(4H) + 2(6H)
= 2H + 3H +10H - 2(10H) + 2(4H) + 2(6H)
= 15H + - 20H + 20H
= 0
Example 2. Find 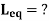

 5H + 6H + 9H - 2(1H) -2(5H) -2(3H)
5H + 6H + 9H - 2(1H) -2(5H) -2(3H)
= 2H
PARALLEL COMBINATION: -
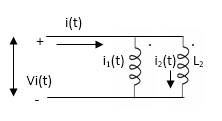
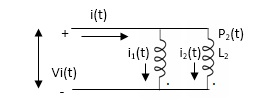
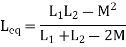
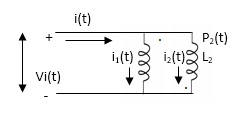
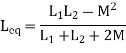
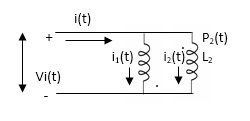
Fig. Parallel Combination

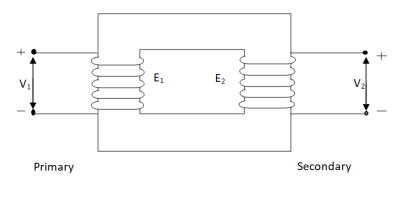
Fig. Ideal Transformer
For above transformer when secondary is open and primary is having input sinusoidal voltage V1. An alternating current flow due to difference in potential. As primary coil is purely inductive so, Iµ current is drawn through it. This current is very small and logs V1 by 900.
The current Iµ produces magnetic flux φ and hence are in same phase. The flux is linked with both the windings and hence, self-induced emf is produced E1 which is equal and opposite of V1. Similarly, E2 is induced in secondary which is mutually induced emf E2 is proportional to rate of change of flux and number of secondary windings.

The phasor is shown below.
Fig. Phasor for Ideal Transformer
Emf Equation of Transformer:
N1 = No of primary turns
N2 = No of secondary turns
Φm = max flux in cone (wb)
Φm = Bm x A
f = Frequency of input(ac) Hz
Average rate of change of flux
= Φm / ¼
= 4 ΦmF volts
Average emf per turn = 4F ΦmV
As Φ varies sinusoidally rms value of induced emf is given as
Form factor = r.m.s value / average value = 1.11
r.m.s value of emf/turn = 1.11 x 4f Φm
= 4.44 f Φm volt
r.m.s value of induced emf in primary winding
= (induced emf/turn) x No of primary turns
E1 = 4.44 fN1 Φm
E1 = 4.44 fN1BmA
r.m.s emf induced in secondary
E2 = 4.44 fN2 Φm
E2 = 4.44 fN2BmA
E1/E2 = N1/N2 = K
K – voltage transformation
(i). If N2 > N1 i.e., K > 1 STEP UP TRASFORMER
(II). If N1 > N2 i.e., K<1 STEP DOWN TRASFORMER
FOR Ideal Transformer
V1 I1 = V2 I2 = 1/K
Hence, current is inversely proportional to the voltage transformation ratio.
Key takeaway
r.m.s value of induced emf in primary winding E1 = 4.44 fN1 Φm
r.m.s emf induced in secondary E2 = 4.44 fN2 Φm
(i). If N2 > N1 i.e., K > 1 STEP UP TRASFORMER
(II). If N1 > N2 i.e., K<1 STEP DOWN TRASFORMER
FOR Ideal Transformer
V1 I1 = V2 I2 = 1/K
Q1>. A 25 KVA transformer has 500 turns on primary and 50 on secondary. The primary is connected to 2000V, 50 Hz supply. Find full load primary and secondary currents, the secondary emf and max flux in core. Neglect leakage drop and no load primary current.
Sol K = N2/N1 = 50/500 = 1/10
I1 = 25,000/2000 = 12.5 A
I2 = I1/K = 10 x 12.5 A = 125 A
Emf/turn on primary side = 2000/500 = 4 V
E2 = KE1
E2 = 4 x 50 = 200 v
E1 = 4.44fN1 Φm
2000 = 4.44 x 50 x 500 x Φm
Φm = 18.02 m Wb
References:
Education, 2013.
4. C. K. Alexander and M. N. O. Sadiku, “Electric Circuits”, McGraw Hill Education, 2004.
5. K. V. V. Murthy and M. S. Kamath, “Basic Circuit Analysis”, Jaico Publishers, 1999.