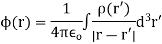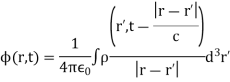Unit - 2
The Continuity Equation
Let q charges in a cube of volume V, come out from a surface. If there is a flow of charge that means current will be there. As the current flows there will be decrease in charges present inside the cube with respect to time.
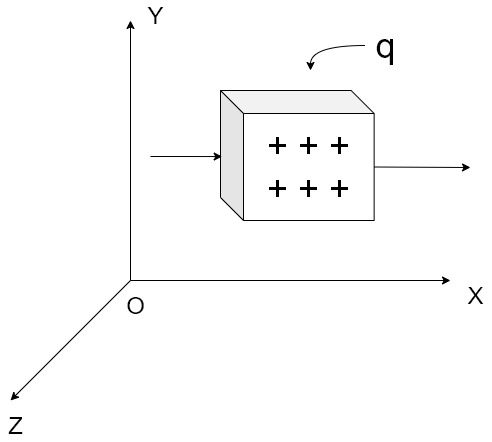
Fig 1 Charge q placed on surface
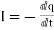 ---------1
---------1
Where 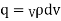
And 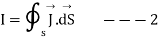
From the law of conservation of charge
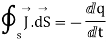
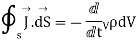
Applying Gauss Divergence theorem
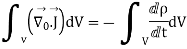
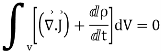
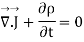
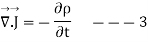
Equation 3 is known as equation of continuity
Key takeaway
“Divergence of constant density is always equal to negative rate of charge of volume charge density “.
Explanation: suppose a coil has n turns and flux through it change from initial value of Ø1 to Ø2 in line t sec
Initial flux linkage = N Ø
Final flux linkage = NØ2
Induced emf e 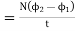
Putting the above equation in differential form
e = rate of change of flux linkage

The direction of this induced emf is given by lenis law which states the polarity of induced emf is always such that it tends to set up a current which flow in such a direction so as to oppose the cause that produces it.
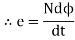
|
|
|
Key takeaway
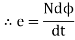
Conduction current occurs in conductors where there are a large number of free electrons. Conduction current occurs due to the drift motion of electrons (charge carriers). Conduction current obeys ohm’s law. When an external electric field is applied to a metallic conductor, conduction current occurs due to the drift of electrons.
The charge inside the conductor experiences a force due to the electric field and hence should accelerate but due to continuous collision with atomic lattice, their velocity is reduced. The net effect is that the electrons moves or drifts with an average velocity called the drift velocity (υd) which is proportional to the applied electric field (E).
Hence according to Newton’s law, if an electron with a mass m is moving in an electric field E with an average drift velocity υd, the average change in momentum of the free electron must be equal to the applied force (F = – e E).
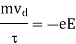
Where is the average time interval between collision.
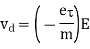
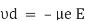
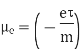
Key takeaway
Conduction current occurs in conductors where there are a large number of free electrons. Conduction current occurs due to the drift motion of electrons (charge carriers).
Convection current occurs in insulators or dielectrics such as liquid, vacuum. Convection current results from motion of electrons or ions in an insulating medium. Since convection current doesn’t involve conductors, hence it does not satisfy ohm’s law. Consider a filament where there is a flow of charge ρv at a velocity u = uy ay.

Fig 2 Filament
The current is given as

But we know 
Hence 
Again, we also know that 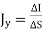
Hence 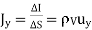
Where uy is the velocity of the moving electron or ion and ρv is the free volume charge density.
Key takeaway
Convection current occurs in insulators or dielectrics such as liquid, vacuum. Convection current results from motion of electrons or ions in an insulating medium.
When a capacitor is charging (or discharging), current flows in the circuit. However, there is no actual charge transfer in the insulated region between capacitor which is contradictory to the flow of current. Hence, displacement current is the current in the insulated region due to the changing electric flux.
For a charged capacitor, electric field between the plates is given by:
E=εoAQ
Q=εoϕE
Displacement current is given by:
id=dtdQ=εodtdϕE
According to Maxwell's Ampere circuital Law, the line integral of magnetic field along a closed path is equal to μo times the total current.
∮B. dl=μo(ic+id)
where ic: Conduction current
id: Displacement current
∮B. dl=μo(ic+εodtdϕ)
Problem:
A parallel-plate capacitor with plate area of 5 cm2 and plate separation of 3 mm has a voltage 50 sin 103 t V applied to its plates. Calculate the displacement current assuming = 2 0.
Solution:
D = E = V/d
Jd = 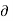 D/
D/  t = dV/dt
t = dV/dt
Hence
Id = Jd . S = S /d dV/dt = C dV/dt
which is the same as the conduction current given by
Ic = dQ/dt = S d*/dt = S dD/dt = S dE/dt + S/d dV/dt = C dV/dt.
Id = 2. 10 -9 /36 . 5 x 10 -4/ 3 x 10 -3 . 10 3 x 50 cos 10 3 t
= 147. 4 cos 10 3 t nA
Faraday’s law stated as:
e.m. f d/dt ɸ----------[V] -------------------------------------------- (1)
This equation implies a closed path.
If the closed path taken by N turns conductor, then,
Emf = -N d/dt ɸ -----------------------------------------------------------(2)
Emf = 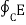 . dl ------------------------------------------------------------------------(3)
. dl ------------------------------------------------------------------------(3)
Also, magnetic flux ɸ =  . dS
. dS
Then
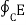 . dl = -
. dl = -  /
/ 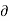 t
t 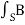 . dS ---------------------------------------------------------(4)
. dS ---------------------------------------------------------(4)
This equation is the integral form of Maxwells equation.
Apply Stokes theorem
 . dl =
. dl =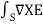 . dS
. dS
Eq(4) becomes 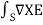 . dS = -
. dS = - 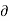 /
/ 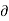 t
t 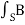 . dS
. dS
That is
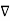 X E = -
X E = - 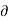 /
/ 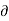 t B ---------------------------------------------------------------(5)
t B ---------------------------------------------------------------(5)
This is Maxwell’s equation in differential form
Which means that a time- changing magnetic field B(t) produces an electric field, E, it has a property of circulation, its line integral about a general closed path isn’t zero.
Key Takeaway:
Maxwell's equations in integral form are field quantities which have to do with the line and surface integrals of the electric and magnetic field vectors.
For time varying case, the relationship among the field vectors written as
 -------1
-------1
 ----2
----2
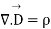 -----3
-----3
 --------4
--------4
In addition, from the principle of conservation of charges we get the equation of continuity
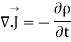
The equation must be consistent with equation of continuity We observe that
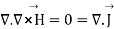 -----5
-----5
Since 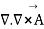 is zero for any vector
is zero for any vector
Thus 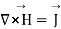 applies only for the static case i.e., for the scenario when
applies only for the static case i.e., for the scenario when
Suppose we are in the process of charging up a capacitor as shown in figure
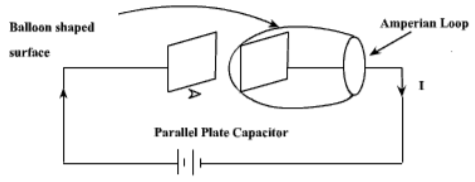
Fig 3 Charging of Capacitor
Let us apply the Ampere's Law for the Amperian loop shown in figure. Ienc = I is the total current passing through the loop. But if we draw a balloon shaped surface as in figure, no current passes through this surface and hence Ienc = 0.
But for non-steady currents such as this one, the concept of current enclosed by a loop is ill-defined since it depends on what surface you use.

= (1)
(1)
=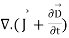 (2)
(2)
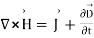 (3)
(3)
The equation (3) is valid for static as well as for time varying case. Equation (3) indicates that a time varying electric field will give rise to a magnetic field even in the absence of the term  has a dimension of current densities (A/m2) and is called the displacement current density.
has a dimension of current densities (A/m2) and is called the displacement current density.
The modified set of equations
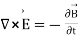 (4)
(4)
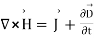 (5)
(5)
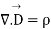 (6)
(6)
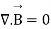 (7)
(7)
is known as the Maxwell's equation and this set of equations apply in the time varying scenario, static fields in this case are 

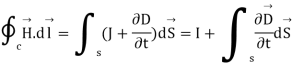
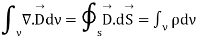
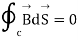
The modification of Ampere's law by Maxwell has led to the development of a unified electromagnetic field theory. By introducing the displacement current term, Maxwell could predict the propagation of EM waves.
Key takeaway
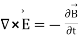
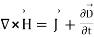
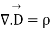
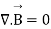
is known as the Maxwell's equation
The solution of poisons or Laplace Equation should always satisfy certain conditions at the boundaries between different media in the field. These conditions pertaining to potential normal component of the displacement vector, tangential component of the electric field intensity and refraction lines of forces are called boundary conditions. This boundary conditions will now be described in detail.
(i) “Potential”: - the electrostatic potential V must be satisfied the following conditions
a. It must go to zero at infinite if charge distribution is of extent.
b. It must be constant throughout any conductor, because it has been assume that all charges are at rest.
c. It must be continuous across any boundary, because this continuous potential would mean and finitely large field intensity which is physically not possible.
(i)Normal component of the displacement vector: -
Consider a pill box shown in figure 15.
The height of pillbox is such that the area of the side surface is small compound to itself should be small so that so that may be constant over.
itself should be small so that so that may be constant over.
Applying Gauss law to a small pill box region
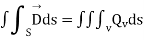
If there is free charge of surface density
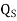 applied to the surface then
applied to the surface then
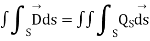

Figure 4. Normal component of displacement vector
Since the total flux out of the pillbox must be equal to the charge and close, we have,
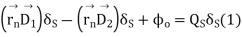
Where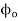 is the flux out of side surface which can be neglected since it has been assumed above that side surface is small
is the flux out of side surface which can be neglected since it has been assumed above that side surface is small
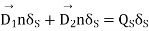
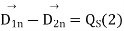
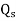 is normally zero at a dielectric boundary, hence equation 2 to will reduce to
is normally zero at a dielectric boundary, hence equation 2 to will reduce to
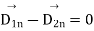

Thus, we conclude that there are two cases of boundary and their conditions are as
a) Saint boundaries between the two media the normal component of flux density or displacement is continuous across the charge free boundary A.
b) When the boundary is between a medium and dielectric that is when medium 2 is a conductor
 from equation 3
from equation 3
The normal component will be zero and 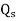 will be the free charge density on the surface of the conductor.
will be the free charge density on the surface of the conductor.
(i)Tangential component of electric intensity E: -
Consider a rectangular loop part abcd shown in figure 20. We know that for any closed path
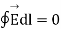

Integrals can be neglected since
can be neglected since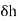 is small and since
is small and since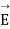 is assumed finite. Hence the above expression reduced to
is assumed finite. Hence the above expression reduced to
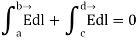

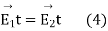
Is medium 2 is a conductor
And hence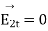 (5)
(5)
Again, two cases will arise
(a)When the boundary is between the two media, tangential component of electric field intensity is continuous across the boundary from equation 4.
(b)When the boundary is between medium and a conductor, the tangential component is zero in both media. Hence the field intensity E is always normal to the surface of the earth
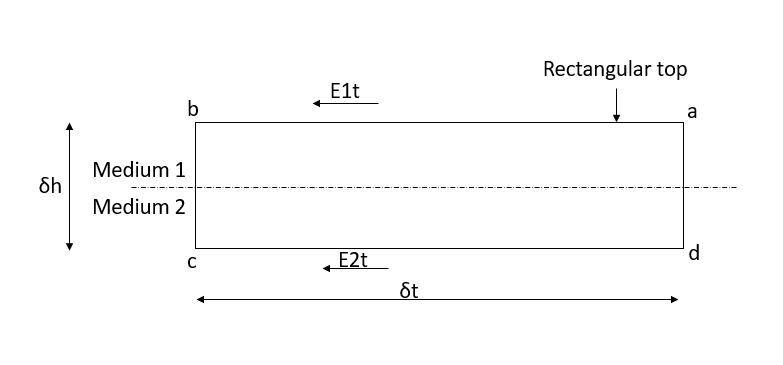
Figure 5. Tangential component of E
(i) “Refraction”: -
Consider two isotropic dielectric media 1 and 2 separated by a charge free boundary as shown in figure (21). Then isotropic media D and E half the same direction so that
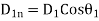
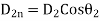
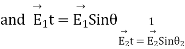
Where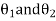 the angle which the incident (in medium 1) and refracted line (in medium 2) makes with normal.
the angle which the incident (in medium 1) and refracted line (in medium 2) makes with normal.
Applying boundary conditions from equation 4 and 5.
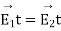

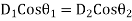

Dividing first by second, we have
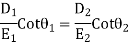

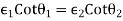
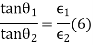
Thus, we conclude from equation 6
(a)The flux lines bend closer to the normal in the lower dielectric constant material.
(b)The field intensity, however will be greater in this material
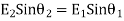

Fig 5 Bending of lines of force
(ii) “Uniqueness theorem”
This theorem states that the potential function as a harmonic function is uniquely determined within a closed, regular region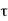 of a dielectric by its value on the boundary surface of the region.
of a dielectric by its value on the boundary surface of the region.
Proof:
Consider a finite region of space which may contain charged conductions at specified potential, dielectric material of specified properties and volume distribution of recharge with specific densities. Now suppose at each. There are two solutions, 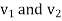 both satisfying poisson’s equation add reducing to specified potentials on the surface conductors
both satisfying poisson’s equation add reducing to specified potentials on the surface conductors
Let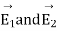 be the electrical intensity is corresponding to
be the electrical intensity is corresponding to 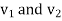 . Then from
. Then from


At every point in the field.
Since 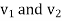 satisfy poisons equation everywhere from equation we have
satisfy poisons equation everywhere from equation we have


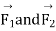 are displacement vectors corresponding to the voltages
are displacement vectors corresponding to the voltages . Let the difference of potential between
. Let the difference of potential between 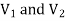 b V. Then
b V. Then
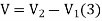
Hence the corresponding displacement vectors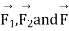 such that
such that
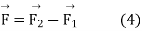

On the surfaces of the conductor at any infinity, v=0 since  reduces to the specified boundary values from a vector identity, we know that
reduces to the specified boundary values from a vector identity, we know that
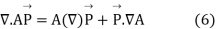
Where A is a scalar quantity and is a vector quantity. Integrating over a volume and using divergence theorem we get
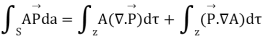
Then if we put A=V and 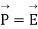 we have
we have
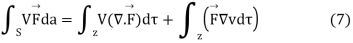
Where surface integral on left hand side is integrated for all the surface which bound the volume over which the integral on the right-hand side is to be evaluated. let's take this volume to be the volume external to the conductors extending to infinity in all directions. The surface integral is then evaluated over all the conductors surfaces and over and imaginary surface of infinite radius. Since the quantity V is zero on all the conductor surface, the portion of integral is zero.
To evaluate the integral over surface of finite radius, since V is zero on all conductor surface the portion of integral is zero.
Consider the integral over a finite sphere and its surface reside to infinity
Both  must fall as
must fall as  at sufficiently large distance, since on to charge appear as a point charge from a distance charge is comparison to the dimension of charge system. Then V the difference between
at sufficiently large distance, since on to charge appear as a point charge from a distance charge is comparison to the dimension of charge system. Then V the difference between 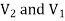 full to
full to 
Now fall as
fall as or as
or as 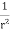
Since area S increases as  the whole integral falls off as
the whole integral falls off as  and approaches zero at infinity. The left hand of equation 9 is zero.
and approaches zero at infinity. The left hand of equation 9 is zero.
The first term on the right-hand side of equation 9 is 0, since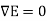 at every point. Therefore, the second term as the right-hand side of equation 9 must be zero, thus
at every point. Therefore, the second term as the right-hand side of equation 9 must be zero, thus
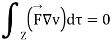
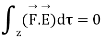
In homogeneous isotropic linear dielectric, the quantity is intrinsically positive. And integral will be zero when
is intrinsically positive. And integral will be zero when equal to zero at every point.
equal to zero at every point.
Then,
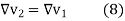
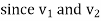 must be same both on the surfaces on the conductors and at infinity must be same everywhere.
must be same both on the surfaces on the conductors and at infinity must be same everywhere.
 and there is one potential V.
and there is one potential V.
NUMERICALS:
Q1. A) Two insulated charged copper spheres A and B half their centres separated by a distance of 50 cm. What is the mutual force of repulsion if charge on each is  coulomb? The radii of A and B is negligible compared to distance of separation.
coulomb? The radii of A and B is negligible compared to distance of separation.
B) What is the force of repulsion of each sphere is charged double of the above amount and the distance between them is halved?
Sol. A) 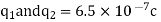
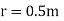
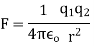
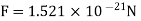
B) 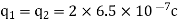



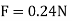
Q2. The electrostatic force on a small sphere of charge 0.4μc due to another small sphere of charge -0.8μc in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Sol. A) Here,



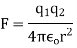

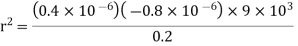
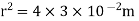

B) Force on second sphere is same 0.2N=F
Q3. A point charge of 2.0 μc is at the centre of a cubic Gaussian surface 90 cm on edge. What is the electric flux through the surface?
Sol. Here q= 20 μc=2×
L=90 cm
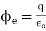 =
= 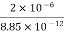
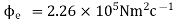
Q4. Consider uniform electric field E, 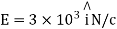
Field is along positive x direction
Surface area =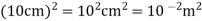
(a)What is the flux of this field through a square of 10 cm on a side whose plane is parallel to y z plane?
(b)What is the flux through the same square is the normal to its plane 30-degree angle with x axis?
Sol.(a) When plane is parallel to y z plane
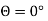
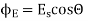
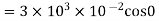
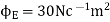
(b)When normal to the plane makes an angle of 30 degree with x-axis then 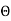 =30°
=30°

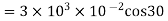
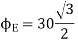

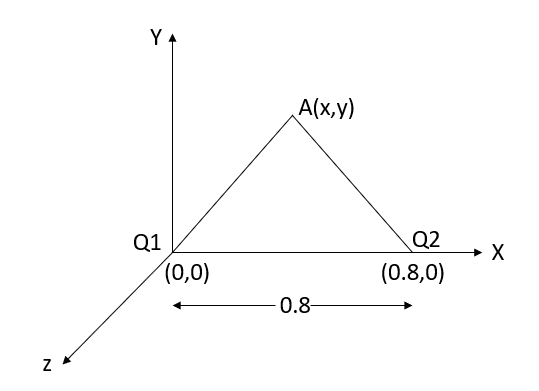
Q5. Two particles having charges 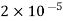 and
and 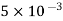 coulombs are spaced 0.8 metre apart. Determine the electric field at a point A situated at a distance of 0.5 metre from each of the particles.
coulombs are spaced 0.8 metre apart. Determine the electric field at a point A situated at a distance of 0.5 metre from each of the particles.
Sol. Let the two particles have charge  coulombs then the point A will be as shown in (1). Let the origin of the three axis be located at the point charge
coulombs then the point A will be as shown in (1). Let the origin of the three axis be located at the point charge  then the coordinates of
then the coordinates of 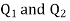 will be (0,0) (0.8,0) respectively.
will be (0,0) (0.8,0) respectively.
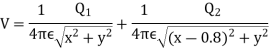
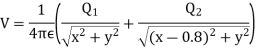
Differentiating partially with respect to x and y we get

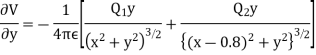
For the location of point A
x=0.4 and y= 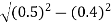 =0.3
=0.3
Substituting these values, we have
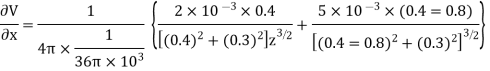



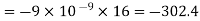
Since the field is desired in xy plane
 and field intensity E is given by
and field intensity E is given by
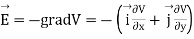
Substituting the values of 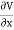 and
and 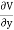 we get
we get
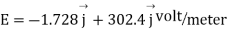
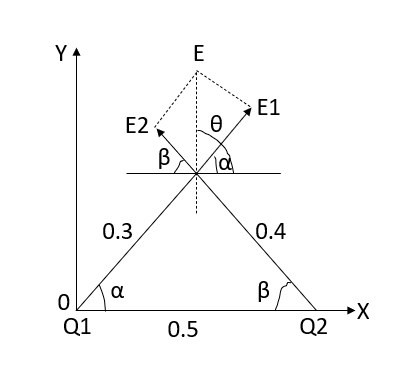
Q6. Determine the electric intensity at a point A located at a distance of 0.3 metre and 0.4 metre respectively from charges 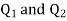 spaced 0.5 metre apart.
spaced 0.5 metre apart. 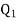 has to charge
has to charge  coulombs while
coulombs while 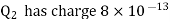 coulombs.
coulombs.
Sol. Let the electric intensity is due to 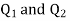 be
be 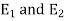 respectively and let the origin be located at
respectively and let the origin be located at  as shown in figure (2). Then the angle
as shown in figure (2). Then the angle 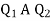 will be 90°.
will be 90°.
The magnitude of the individual intensities from equation will be

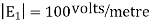
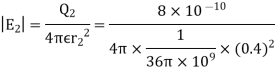
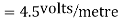
In order to add these intensities vectorially, thin components along x and y direction will be used.
(i) The x component of 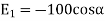
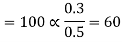
(ii) The x component of 
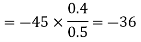
(iii) The y components of 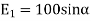
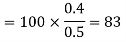
(iv) The y component of 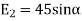
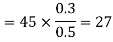
The total x components of 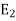 let us say
let us say 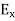 will be
will be
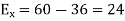
And the total y component of E let us say 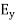 will be
will be
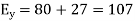
Resultant electric intensity has a magnitude E=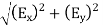




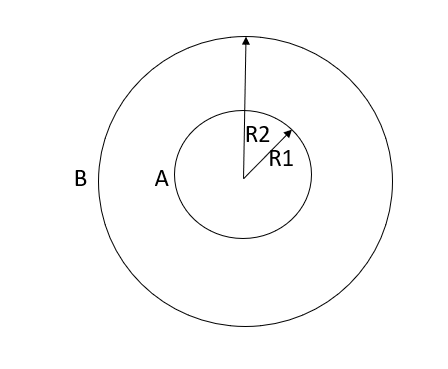
Q7. Derive an expression for the potential difference at any point between spherical shells in terms of applied potential using Laplace Equation.
Sol. Since the medium between shells is uncharged, Laplace Equation can be applied. In spherical coordinates lapis equation is given by
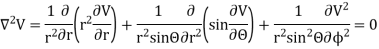
by symmetry the field and therefore the potential function depends upon the radial distance r alone
Therefore,
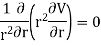
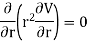
Integrating we have


Integrating again
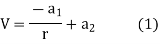
If the radius of spherical shells A and B are 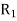 and R and v is the voltage we have
and R and v is the voltage we have
When, 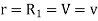
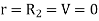
Substituting these values in equation (1)
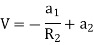

Solving these two equations for 
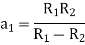
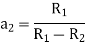
Substituting values of 
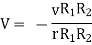
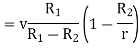
Q8. A positive charge of 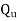 coulombs per cubic metre occupies the volume of sphere. At point in the inferior at a distance r from the centre, a small proverb charge of +2 is inserted. What is the force acting on the probe charge?
coulombs per cubic metre occupies the volume of sphere. At point in the inferior at a distance r from the centre, a small proverb charge of +2 is inserted. What is the force acting on the probe charge?
Sol. Force P on the probe charge at a point P lying at t a distance r from the centre, as shown in fig.
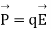
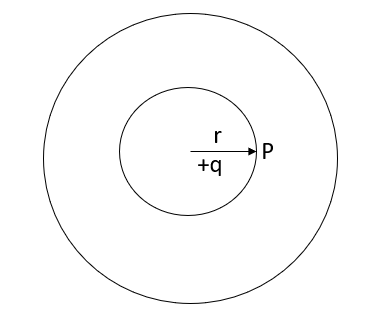
Figure A small probe charge +2 inserted at a distance r from the centre
On applying Gaussian law will yield

But the surface of sphere 
Therefore, 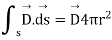
While the volume of a sphere is 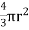
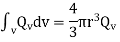
Putting these values in above equation we get
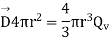
We know that,
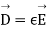
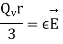
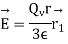
Putting this value of E in  we get
we get
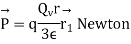
Q9. Using Laplace Equation, determine the field intensity over a gap between coaxial cylinders.
Sol. Let the inner and outer radius of the coaxial cylinder be 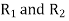 respectively as shown in figure. We have to determine the field within the coaxial cylinder subject to boundary condition.
respectively as shown in figure. We have to determine the field within the coaxial cylinder subject to boundary condition.
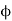
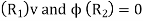
Since the nature of boundaries are of cylindrical nature, writing Laplace Equation in cylindrical form
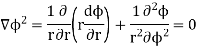
If the cable is long, then except near ends there will be no variation with z. Father because of cylindrical symmetry potential cannot be a function of  so equation reduces to
so equation reduces to

Integrating the differential equation twice we have
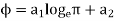
Where 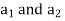 are constants of integration and can be evaluated from the boundary conditions
are constants of integration and can be evaluated from the boundary conditions
Thus, 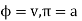

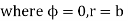
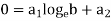
Solving above two equations we have
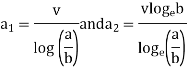
Putting these values of 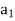 and
and  above
above
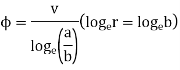
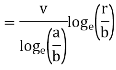



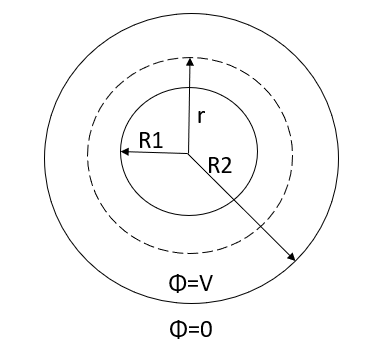
Figure Cross section of coaxial cylinder
Q10. A point charges 1, -2, -3 and 3μc are located on the x-axis at x=1,2,3 and 4 meter respectively. What energy is stored in the field.
Sol. Energy stored=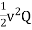
Let us find out the potential V using equation.
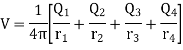

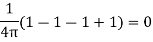
Hence energy stored in the field is zero.
Q11. A radio antenna 1 cm diameter conductor is stretched horizontally 10 metre above the ground. Determine the capacitance of the antenna per unit length. Neglect the end effects and consider the ground to be perfect.
Sol. h= 10 metres
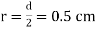
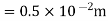
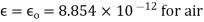
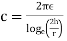
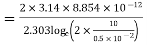 farad
farad

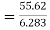 p farad
p farad

Q12. A 2 μF capacitor is charged by connecting it across a 100 V DC supply is now disconnected and the capacitor connected across another 2 μF capacitor. Assuming no leakage, determine the potential difference between the plates of each capacitor and energy connected on amount of energy stored as 2 cases.
Sol. When the capacitor is connected across a 100 V D.C energy stored 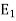 is given by
is given by
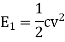
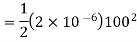
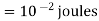
Now with 100 v supply this capacitor is charged and charge capacitor is charged and charge Q accumulated on 2 μF capacitor is
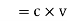
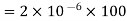
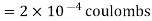
Where 100 v D.C supply is replaced by another capacitor of 2 μF. The charge 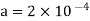 coulombs get redistributed to a common potential V such that
coulombs get redistributed to a common potential V such that

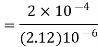
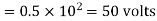
Energy stored 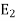 is given by
is given by

Loss of energy=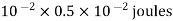
In steady-state, Maxwell's equations reduce to
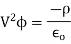
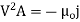
The solutions to these equations are easily found using the Green's function for Poisson's equation
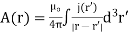
The time-dependent Maxwell equations reduce to


We can solve these equations using the time-dependent Green's function. We find that
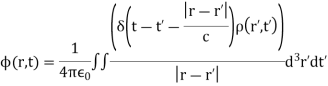
with a similar equation for 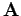 . Using the well-known property of delta-functions, these equations reduce to
. Using the well-known property of delta-functions, these equations reduce to
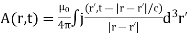
However, when we calculate the contribution of charges and currents at position 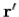 to these integrals we do not use the values at time
to these integrals we do not use the values at time 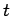 , instead we use the values at some earlier time. It is simply the latest time at which a light signal emitted from position
, instead we use the values at some earlier time. It is simply the latest time at which a light signal emitted from position  would be received at position
would be received at position  before time
before time  . This is called the retarded time. Likewise, the potentials are called retarded potentials. It is often useful to adopt the following notation
. This is called the retarded time. Likewise, the potentials are called retarded potentials. It is often useful to adopt the following notation

The square brackets denote retardation (i.e., using the retarded time instead of the real time). Therefore, we get
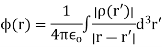
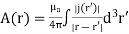
The time dependence in the above equations is taken as read.
We are now able to understand electromagnetism at its most fundamental level. A charge distribution (r,t) can thought of as built up out of a collection, or series, of charges which instantaneously come into existence, at some point 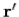 and some time
and some time 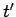 , and then disappear again. Mathematically, this is written
, and then disappear again. Mathematically, this is written
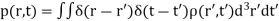
Likewise, we can think of a current distribution j(r,t) as built up out of a collection or series of currents which instantaneously appear and then disappear:
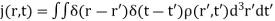
Each of these ephemeral charges and currents excites a spherical wave in the appropriate potential. Thus, the charge density at 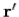 and
and 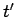 sends out a wave in the scalar potential:
sends out a wave in the scalar potential:

Likewise, the current density at 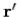 and
and 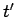 sends out a wave in the vector potential:
sends out a wave in the vector potential:

Key takeaway
The solutions to these equations are easily found using the Green's function for Poisson's equation
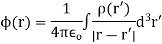
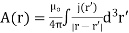
Instantaneous pointing vector is used to find Average pointing vector.
So average pointing vector
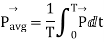

For perfect dielectric or free space

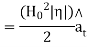
Complex pointing vector: -
Poynting vector is a nonlinear function of the fields.
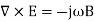
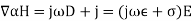
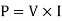
Compute the quantity

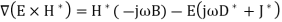
Applying the Divergence theorem
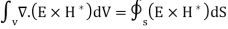
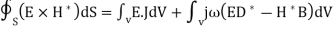
Defining  and
and 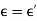 since most materials are non magnetic ignoring magnetic losses.
since most materials are non magnetic ignoring magnetic losses.
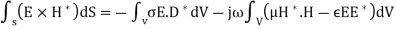
We can see the first volume integral is a real number whereas the second volume integral is imaginary.
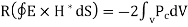

Now compute the average vector S
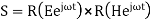
Observing that
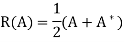
So that 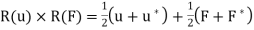
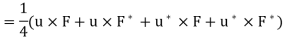
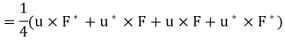
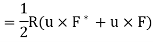
So, compute pointing vector with time dependence

Taking average value

Key takeaway
Quantity 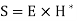 shows the power stored in the field.
shows the power stored in the field.
Poynting theorem states that the net power flowing out of a given volume V is equal to the time rate of decrease of stored electromagnetic energy in that volume decreased by the conduction losses is the total power leaving the volume = rate of decrease of stored electromagnetic energy ohmic power dissipated due to motion of charge.
Proof:
The energy density carried by the electromagnetic wave can be calculated using Maxwell's equations
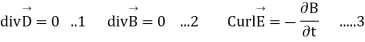

 (5)
(5)
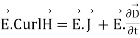 (6)
(6)
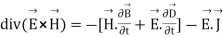 (7)
(7)
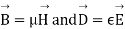
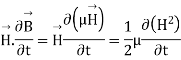
=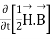

So, from equation (vii) 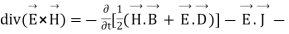
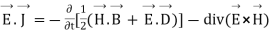 (viii)
(viii)
Integrating equation (viii) over a volume V enclosed by a surface S
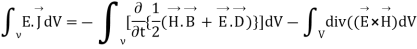
Or 
As 
or 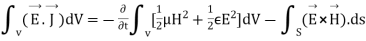
or 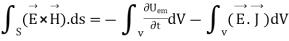
or 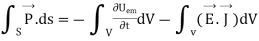
that is the Total power leaving the volume = rate of decrease of stored e.m.f energy - ohmic power dissipated due to charge motion
Key takeaway
This equation (ix) represents the poynting theorem according to which the net power flowing out of a given volume is equal to the rate of decrease of stored electromagnetic energy in that volume minus the conduction losses.
References: