Unit – 1
Introduction
Artificial intelligence (AI) is a branch of study concerned with assisting robots in finding human-like solutions to difficult issues. This usually requires turning characteristics of human intellect into computer-friendly algorithms. A more or less flexible or efficient technique may be chosen depending on the requirements, which defines how artificial the intelligent behavior appears.
Although artificial intelligence is most generally associated with computer science, it has multiple important ties with other fields such as mathematics, psychology, cognition, biology, and philosophy, to mention a few. Our capacity to synthesize information from all of these domains will help us progress in our quest to create an artificially intelligent being.
Artificial intelligence currently encompasses a wide range of subfields, from general-purpose areas like vision and logical reasoning to specialized vocations like chess, mathematical theorems, poetry production, and disease diagnosis.
Often, scientists from other fields flock to artificial intelligence because it provides them with the tools and vocabulary they require to systematize and automate the cognitive processes they've been working on for their whole careers. Employees of AI can also apply their skills to any sphere of human intellectual endeavor. In this respect, it is genuinely a universal field.
Key takeaway
An AI system is made up of an agent and its surroundings. The agents are constantly interacting with their environment. Other agents in the environment could be present.
Any object with sensors that can sense its surroundings and effectors that can act on that environment is considered an agent.
● Human agents: Sensory organs like the eyes, ears, nose, tongue, and skin are parallel to the effector organs like the hands, legs, and mouth. Organs such as the hands, legs, and mouth are parallel to the effectors.
● Robotics agents: A robotic agent replaces cameras and infrared range finders as sensors, and various motors and actuators as effectors.
● Software agents: A software agent's programs and activities are encoded bit strings.
Sensor: A sensor is an electronic device that detects and communicates data about changes in the environment to other electronic devices. Sensors allow an agent to see what's going on around it.
Actuator: Actuators are the parts of machines that convert energy into motion. The main purpose of actuators is to move and control a system. Anything from an electric motor to gears to rails can be used as an actuator.
Effectors: Effectors are gadgets that have an environmental impact. Effectors include things like legs, wheels, arms, fingers, wings, fins, and a display screen.
Everything in the world that surrounds an agent is his or her environment, but it is not a part of him or her. An environment refers to the setting in which an agent is present.
The agent's environment is defined as the place where he or she lives, works, and has something to detect and respond to. The bulk of the time, a setting is labeled as non-feminist.
Key takeaway
The state of being reasonable, sensible, and having a good sense of judgment is known as rationality.
Rationality is concerned with the actions and consequences that can be foreseen based on the agent's views. Taking actions with the objective of obtaining useful knowledge is a fundamental part of reason.
The rationality of an agent is determined by its performance metric. To determine reasonableness, utilize the following criteria:
● The success criterion is defined by a performance metric.
● The agent has prior knowledge of its surroundings.
● The most effective activities that an agent can take.
● The order in which percepts appear.
The Nature of Environments
Some programs operate in an entirely artificial environment, relying solely on keyboard input, databases, computer file systems, and character output on a screen.
On the other hand, some software agents (software robots or softbots) exist in rich, unlimited softbots domains. The simulator's environment is incredibly detailed and complex. The software agent must choose among a vast number of possibilities in real time. In both a real and an artificial setting, a softbot examines a customer's internet interests and offers appealing things to them.
The Turing Test is the most well-known artificial scenario, in which one real and other artificial agents are put to the test on an equal footing. Because a software agent cannot perform as effectively as a human, this is a challenging environment to work in.
Turing test
The Turing Test can be used to determine whether a system's intelligent behavior is successful.
Two humans will participate in the test, as well as a machine that will be checked. One of the two individuals is assigned to the role of tester. They're all in separate rooms. The tester has no way of knowing who is human and who is not. He types the questions and transmits them to both intelligences, who react with typed answers.
The goal of this test is to deceive the tester. The machine is deemed to be intelligent if the tester is unable to distinguish the machine's response from the human response.
The structure of Agents
The goal of AI is to construct an agent program that can perform the functions of an agent. An intelligent agent's framework is made up of the architecture and the agent program. In a nutshell, it goes like this:
Agent = Architecture + Agent program
The following are the three most important terms in the structure of an AI agent:
Architecture: Architecture is the machinery on which an AI agent operates.
● Architecture = the machinery that an agent executes on.
Agent function: The agent function is used to map a percept to a certain action.
● f:P* → A
Agent program: An agent program is a program that performs the function of an agent. To produce function f, an agent program runs on the physical architecture.
● Agent Program = an implementation of an agent function.
Key takeaway
In Artificial Intelligence, search techniques are universal problem-solving procedures. To solve a given problem and deliver the optimum outcome, rational agents or problem-solving agents in AI used these search techniques or algorithms. Problem-solving agents are goal-based agents that use atomic representation. In this subject, we will explore a variety of problem-solving search approaches.
Searching Algorithms Terminologies:
● Search: In a given search space, searching is a step-by-step procedure for addressing a search problem. There are three primary variables that can influence the outcome of a search:
○ Search space: A search space is a collection of probable solutions that a system could have.
○ Start state: It's the starting point for the agent's quest.
○ Goal test: It's a function that looks at the current state and returns whether or not the goal state has been reached.
● Search tree: Search tree is a tree representation of a search problem. The root node, which corresponds to the initial state, is at the top of the search tree.
● Actions: It provides the agent with a list of all available actions.
● Transition model: A transition model is a description of what each action does.
● Path cost: It's a function that gives each path a numerical cost.
● Solutions: It is an action sequence that connects the start and end nodes.
● Optimal solutions: If a solution is the cheapest of all the options.
Formulating problems
The problem of getting to Bucharest had been previously defined in terms of the starting state, activities, transition model, goal test, and path cost. Despite the fact that this formulation appears to be reasonable, it is still a model—an abstract mathematical description—rather than the real thing.
Compare our simple state description, In (Arad), to a cross-country trip, where the state of the world includes a wide range of factors such as the traveling companions, what's on the radio, the scenery out the window, whether there are any law enforcement officers nearby, how far it is to the next rest stop, the road condition, the weather, and so on.
All of these factors aren't mentioned in our state descriptions because they have nothing to do with finding a route to Bucharest. The process of removing details from a representation is known as abstraction.
In addition to the state description, we must abstract both the state description and the actions themselves. A driving action can result in a number of different outcomes. It takes time, consumes fuel, emits emissions, and changes the agent, in addition to shifting the vehicle's and its occupants' positions (as they say, travel is broadening). In our system, only the change in position is taken into account.
Can we be more precise about the proper level of abstraction? Consider the abstract states and actions we've selected as large collections of detailed world states and action sequences. Consider a path from Arad to Sibiu to Rimnicu Vilcea to Pitesti to Bucharest as an example of a solution to the abstract problem. A wide number of more detailed paths correlate to this abstract solution.
Searching for solution
We must now address the issues we've identified. Because a solution consists of a series of activities, search algorithms consider a number of different action sequences. The SEARCH TREE possible action sequences start with the starting state and build a search tree with the initial state NODE at the root; the branches are actions, and the nodes are states in the problem's state space.
Figure depicts the first few steps in developing a search tree for finding a route from Arad to Bucharest. The root node of the tree represents the initial state (Arad). The first stage is to determine whether or not this is a goal state. (Of course, it isn't, but it's worth double-checking to avoid problems like "starting in Arad, get to Arad.") Then we must weigh a number of possibilities. This is done by extending the current state; in other words, each legal action is applied to the existing state, resulting in the production of a new set of states. In this scenario, we create three additional child nodes from the parent node In(Arad): In(Sibiu), In(Timisoara), and In(Sibiu) (Zerind).
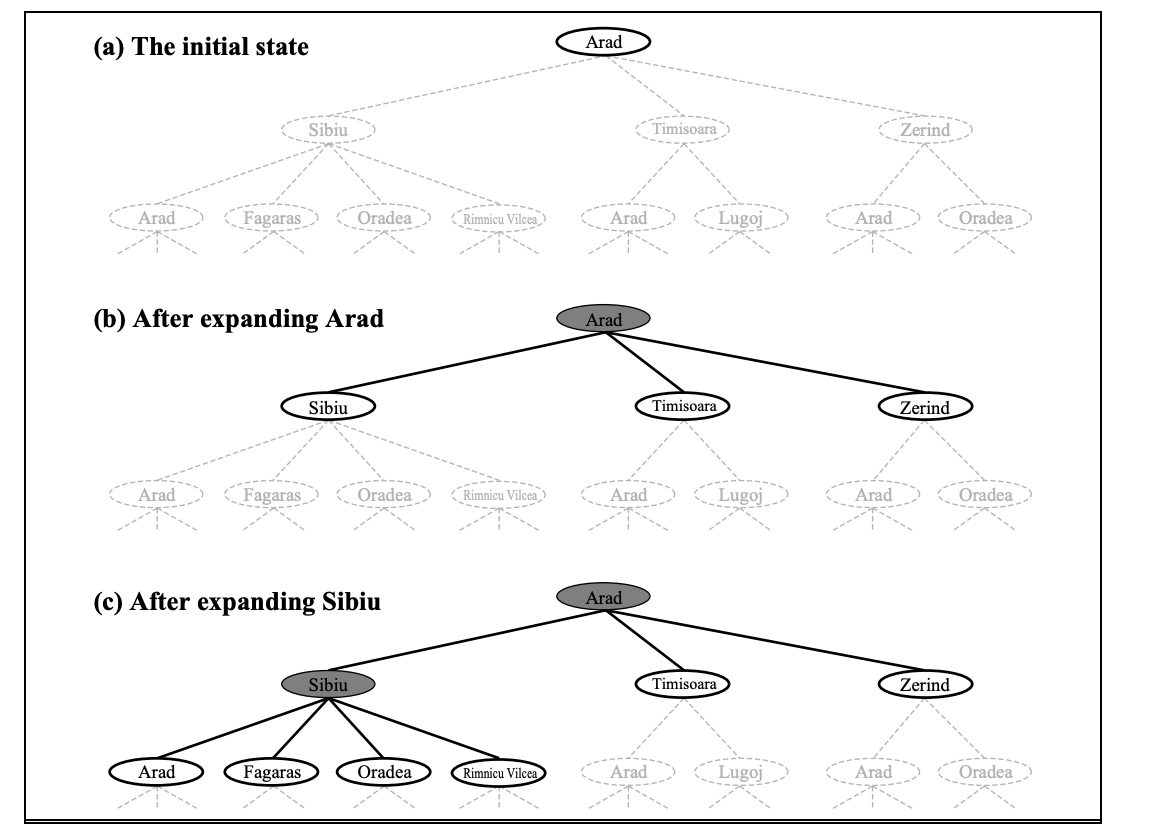
Fig 1: Partial search tree
This is the essence of searching: pursuing one option at a time while putting the others on hold in the event that the first does not yield a solution. Let's use Sibiu as an example. We first check to see whether it's a target state (it isn't), then expand it to get In(Arad), In(Fagaras), In(Oradea), and In(Oradea) (RimnicuVilcea). Then we can choose one of these four possibilities, or we can go back to LEAF NODE and choose Timisoara or Zerind. Each of these six nodes in the tree is a leaf node, which means it has no progeny.
At any given FRONTIER point, the frontier is the collection of all leaf nodes that are available for expansion. Each tree's border is defined by the nodes with bold outlines in Figure.
The process of choosing and expanding nodes on the frontier continues until a solution is found or no more states can be added to the frontier. Informally, the TREE-SEARCH algorithm is depicted in the figure. All search algorithms have the same core basis; the difference is in how they choose which state to expand next—the so-called search strategy.
function TREE-SEARCH (problem) returns a solution, or failure
initialize the frontier using the initial state of problem
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution
expand the chosen node, adding the resulting nodes to the frontier
function GRAPH-SEARCH(problem) returns a solution, or failure
initialize the explored set to be empty
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution
add the node to the explored set
expand the chosen node, adding the resulting nodes to frontier
only if not in the frontier or explored set
Fig 2: An informal description of the general tree-search and graph-search algorithms.
Key takeaway
Uninformed search, also known as blind, exhaustive, or brute-force search, is a type of search that doesn't use any information about the problem to guide it and so isn't very efficient.
Breadth first search
The breadth first search technique is a general strategy for traversing a graph. A breadth first search takes up more memory, but it always discovers the shortest path first. In this type of search, the state space is represented as a tree. The answer can be discovered by traveling the tree. The tree's nodes indicate the initial value of starting state, multiple intermediate states, and the end state.
This search makes use of a queue data structure, which is traversed level by level. In a breadth first search, nodes are extended in order of their distance from the root. It's a path-finding algorithm that, if one exists, can always find a solution. The answer that is discovered is always the alternative option. This task demands a significant amount of memory. At each level, each node in the search tree is increased in breadth.
Algorithm:
Step 1: Place the root node inside the queue.
Step 2: If the queue is empty then stops and returns failure.
Step 3: If the FRONT node of the queue is a goal node, then stop and return success. Step 4: Remove the FRONT node from the queue. Process it and find all its neighbours that are in a ready state then place them inside the queue in any order.
Step 5: Go to Step 3.
Step 6: Exit.
Implementations
Let us implement the above algorithm of BFS by taking the following suitable example
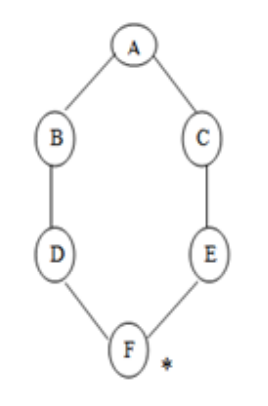
Fig 3: Example
Consider the graph below, where A is the initial node and F is the destination node (*).
Step 1: Place the root node inside the queue i.e. A
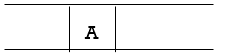
Step 2: The queue is no longer empty, and the FRONT node, i.e. A, is no longer our goal node. So, proceed to step three.
Step 3: Remove the FRONT node, A, from the queue and look for A's neighbors, B and C.
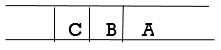
Step 4: Now, b is the queue's FRONT node. As a result, process B and look for B's neighbors, i.e., D.
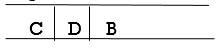
Step 5: Find out who C's neighbors are, which is E.

Ste 6: As D is the queue's FRONT node, find out who D's neighbors are.
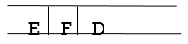
Step 7: E is now the queue's first node. As a result, E's neighbor is F, which is our objective node.
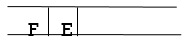
Step 8: Finally, F is the FRONT of the queue, which is our goal node. As a result, leave.
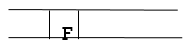
Advantages
● The goal will be achieved in whatever way possible using this strategy.
● It does not take any unproductive pathways for a long time.
● It finds the simplest answer in the situation of several pathways.
Disadvantages
● BFS consumes a significant amount of memory.
● It has a greater level of time complexity.
● It has long pathways when all paths to a destination have about the same search depth.
Key takeaway
DFS is a type of uniform search that is equally important. The vertices of the graph are traversed using DFS. This type of algorithm will always choose to delve deeper into the graph. After visiting all the reachable vertices from a specific source, DFS chooses one of the remaining undiscovered vertices and continues the search.
DFS always produces a child of the deepest unexpanded nod, which serves as a reminder of the breath first search's space constraint. The data structure stack, often known as last in first out, is used by DFS (LIFO). A notable property of DFS is the discovery and finish time of each vertex from a parenthesis structure.
Algorithm:
Step 1: PUSH the starting node into the stack.
Step 2: If the stack is empty then stop and return failure.
Step 3: If the top node of the stack is the goal node, then stop and return success. Step 4: Else POP the top node from the stack and process it. Find all its neighbours that are in ready state and PUSH them into the stack in any order.
Step 5: Go to step 3.
Step 6: Exit.
Implementation:
Let us take an example for implementing the above DFS algorithm.
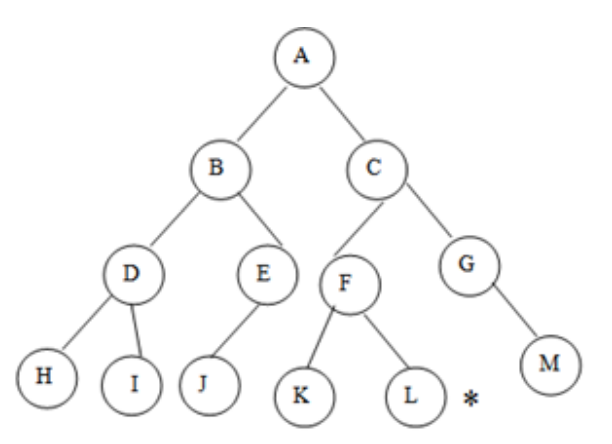
Fig 4: Example
In the graph, A represents the root node and L represents the goal node.
Step 1: PUSH the stack's initial node, i.e.

Step 2: The stack is no longer empty, and A is no longer our objective node. As a result, go to the next step.
Step 3: POP the top node from the stack, A, and look for A's neighbors, B and C.

Step 4: C is now the stack's top node. Look for its neighbors, F and G.
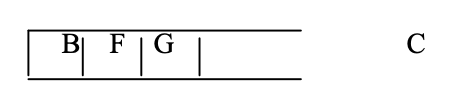
Step 5: G is now the stack's top node. Find its next-door neighbor, M.
Step 6: Now that M is the top node, identify its neighbor. However, since M has no neighbors in the graph, POP it from the stack.

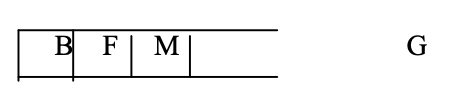
Step 7: Now that F is the top node, and K and L are its neighbors, PUSH them onto the stack.
Step 8: L is now the stack's top node, which is also our goal node.

You can also traverse the graph starting at the root A and inserting C and B onto the stack in that order.
Advantages
● DFS takes up very little memory.
● It will arrive at the goal node in less time than BFS if it takes the correct path.
● It may be able to find a solution without requiring us to sift through a large number of results because we may acquire the desired outcome immediately.
Disadvantages
● Some states may recur in the future.
● There's no guarantee the goal node will be discovered.
● The states may become locked in an endless loop in some situations.
Key takeaway
● After the agent established the starting state, when the world is totally observable and predictable, and the agent knows what the consequences of each action are, perceptions provide no new information.
● Every perception helps the agent narrow the range of possible states in partially viewable environments, making it easier for the agent to achieve its objectives.
● In nondeterministic settings, perceptions indicate the agent which of the alternative outcomes has actually occurred.
● Future perceptions cannot be foreseen in either scenario, and those perceptions will govern the agent's future actions.
● A contingency plan (also known as a strategy) describes what to do depending on the concepts received as a solution to this type of challenge.
A heuristic is a technique for making our search process more efficient. Some heuristics assist in the direction of a search process without claiming completeness, whereas others do. A heuristic is a piece of problem-specific knowledge that helps you spend less time looking for answers. It's a strategy that works on occasion, but not all of the time.
The heuristic search algorithm uses the problem information to help steer the way over the search space. These searches make use of a number of functions that, assuming the function is efficient, estimate the cost of going from where you are now to where you want to go.
A heuristic function is a function that converts problem situation descriptions into numerical measures of desirability. The heuristic function's objective is to direct the search process in the most profitable routes by recommending which path to take first when there are multiple options.
The following procedures should be followed when using the heuristic technique to identify a solution:
1. Add domain—specific information to select what is the best path to continue searching along.
2. Define a heuristic function h(n) that estimates the ‘goodness’ of a node n. Specifically, h(n) = estimated cost (or distance) of minimal cost path from n to a goal state.
3. The term heuristic means ‘serving to aid discovery’ and is an estimate, based on domain specific information that is computable from the current state description of how close we are to a goal.
A search problem in which multiple search orders and the use of heuristic knowledge are clearly understood is finding a path from one city to another.
1. State: The current city in which the traveller is located.
2. Operators: Roads linking the current city to other cities.
3. Cost Metric: The cost of taking a given road between cities.
4. Heuristic information: The search could be guided by the direction of the goal city from the current city, or we could use airline distance as an estimate of the distance to the goal.
Key takeaway
The technique of this method is very similar to that of the best first search algorithm. It's a simple best-first search that reduces the expected cost of accomplishing the goal. It basically chooses the node that appears to be closest to the goal. Before assessing the change in the score, this search starts with the initial matrix and makes all possible adjustments. The modification is then applied until the best result is achieved. The search will go on until no further improvements can be made. A lateral move is never made by the greedy search.
It reduces the search time by using the least estimated cost h (n) to the goal state as a measure, however the technique is neither comprehensive nor optimal. The key benefit of this search is that it is straightforward and results in speedy results. The downsides include the fact that it is not ideal and is prone to false starts.
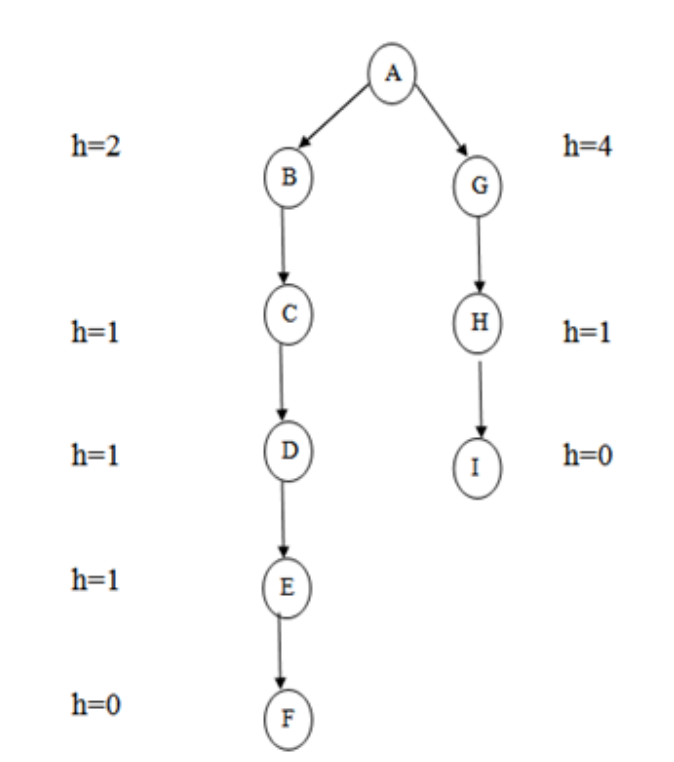
Fig 5: Greedy search
The best first search algorithm is a graph search method that chooses a node for expansion based on an evaluation function f. (n). Because the assessment measures the distance to the goal, the explanation is generally given to the node with the lowest score. Within a general search framework, a priority queue, which is a data structure that keeps the fringe in ascending order of f values, can be utilized to achieve best first search. This search algorithm combines the depth first and breadth first search techniques.
Algorithm:
Step 1: Place the starting node or root node into the queue.
Step 2: If the queue is empty, then stop and return failure.
Step 3: If the first element of the queue is our goal node, then stop and return success.
Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.
Step 5: Go to step-3.
Step 6: Exit
Key takeaway
A* has been a generic word for numerous AI systems from its inception in 1968 by Peter Hart, Nils Nilsson, and Bertram Raphael. It's a mix of Dijkstra's algorithm with the approach of Best First Search. It can be used to solve a variety of problems. A* search seeks the shortest path through a search space to the objective state using a heuristic function.
This strategy looks for low-cost solutions and leads to the A* search target state. The * in A* is written to be as efficient as possible. When transitioning from one state to another incurs a cost, the A* algorithm identifies the least expensive path between the start and goal states.
A* necessitates the use of a heuristic function to determine the cost of a path that travels through a specific state. If the branching factor is finite and every action has a fixed cost, this method is complete. A* necessitates the use of a heuristic function to determine the cost of a path that travels through a specific state. The following formula can be used to determine it.
F (n) = g (n) + h (n)
Where
g (n): The actual cost path from the start state to the current state.
h (n): The actual cost path from the current state to the goal state.
f (n): The actual cost path from the start state to the goal state. For the implementation of A* algorithm we will use two arrays namely OPEN and CLOSE.
OPEN: An array which contains the nodes that has been generated but has not been yet examined.
CLOSE: An array which contains the nodes that have been examined.
Algorithm:
Step 1: Place the starting node into OPEN and find its f (n) value.
Step 2: Remove the node from OPEN, having the smallest f (n) value. If it is a goal node then stop and return success.
Step 3: Else remove the node from OPEN, find all its successors.
Step 4: Find the f (n) value of all successors; place them into OPEN and place the removed node into CLOSE.
Step 5: Go to Step-2.
Step 6: Exit.
Advantages
● It is comprehensive and ideal.
● It is the greatest option among the alternatives.
● It's used to solve really complex problems.
● It is the most efficient approach since no other method guarantees that fewer nodes will be expanded than A*.
Disadvantages
● This method is complete if the branching factor is finite and each action has a set cost.
● The speed with which A* search can be done is determined by the precision of the heuristic approach used to compute h. (n).
● Complexity is a problem for it.
CSP (Constraint Satisfaction Problem)
A constraint satisfaction problem (CSP) consists of
The goal is to pick a value for each variable so that the resulting alternative world fulfills the constraints; we're looking for a constraint model.
CSPs are mathematical problems in which the state of a group of objects must conform to a set of rules.
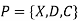
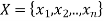
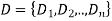

A CSP over finite domains is depicted in the diagram. We have a collection of variables (X), a set of domains (D), and a set of constraints (C) to work with.
The values assigned to variables in X must fall into one of D's domains.
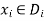
A constraint restricts the possible values of a subset of variables from X.
A finite CSP has a finite number of variables and each variable has a finite domain. Although several of the approaches discussed in this chapter are designed for infinite, even continuous domains, many of them only operate for finite CSPs.
Given a CSP, there are a number of tasks that can be performed:
Key takeaway
The majority of search techniques function in either a forward or backward manner. However, in many cases, a combination of the two is required. With such a hybrid technique, it would be possible to solve the major elements of the problem first, and then deal with the little issues that develop when they are mixed together. One such methodology is "Means-Ends Analysis."
The goal of a means-ends analysis is to figure out how much the current state differs from the desired one. The problem space for means-ends analysis has an initial state and one or more goal states, a set of operations with a set of preconditions for their use, and various functions that compute the difference between two states a(i) and s. (j). The means - ends analysis is used to address a problem
(The first AI program to use means - ends analysis was the GPS General problem solver)
Many human planning activities benefit from means-end analysis. Consider the case of an office worker's planning. Assume we have a different three-rule table:
Key takeaway
References: