1.1 Revision of Number System Introduction to various number systems and their Conversion | unit 1 revision of number system

DSD

Unit - 1

Revision of Number System

1.1 Revision of Number System: Introduction to various number systems and their Conversion

A digital system understands positional number system where there are few symbols called digits and these symbols represents different values depending on their position in the number.

A value of the digit is determined by using

The digit

Its position

The base of the number system

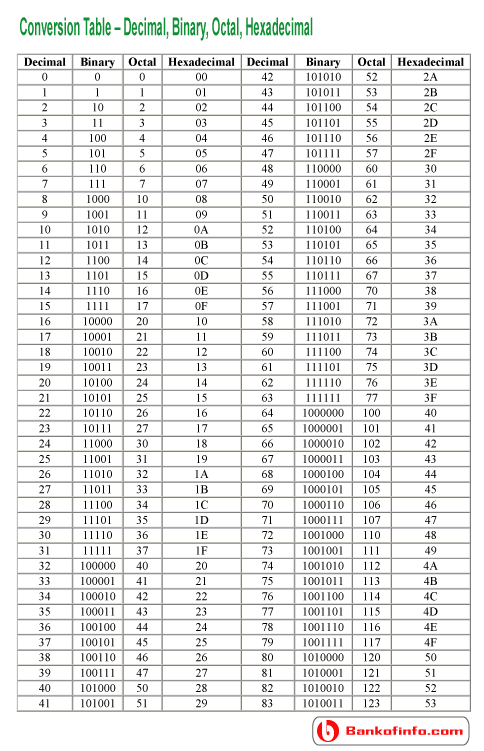
Decimal Number System

It’s the system that we use in our daily life. It has a base 10 and uses 10 digits from 0 to 9.

Here, the successive positions towards the left of the decimal point represent units, tens, hundreds, thousands and so on.

Each and every position represents a specific power of the base (10). For example, the decimal number 4321 consists of the digit 1 in the unit’s position, 2 in the tens position, 3 in the hundreds position, and 4 in the thousands position, and its value can be written as

(1×1000) + (2×100) + (3×10) + (4×l)

(1×103) + (2×102) + (3×101) + (4×l00)

1000 + 200 + 30 + 1

1234

As a computer programmer, we should understand the following number systems used in computers.

S.N.	Number System & Description
1	Binary Number System Base 2. Digits used: 0 and 1
2	Octal Number System Base 8. Digits used: 0 to 7
3	Hexa Decimal Number System Base 16. Digits used: 0 to 9, Letters used: A- F

Binary Number System

It uses two digits 0 and 1.

It is also called as base 2 number system.

Here, each position in any binary number represents a power of the base (2). Example: 23

The last position represents a y power of the base (2). Example: 2y where y represents the last position.

Example

Binary Number: 101112

Calculating the Decimal Equivalent of binary number −

Step	Binary Number	Decimal Number
Step 1	101012	((1 × 24) + (0 × 23) + (1 × 22) + (1 × 21) + (1 × 20))10
Step 2	101012	(16 + 0 + 4 + 2 + 1)10
Step 3	101012	2310

Note: 101112 is normally written as 10111.

Octal Number System

It consists of eight digits 0, 1,2,3,4,5,6,7.

It is also named as base 8 number system.

Here each position represents a power of the base (8). Example: 82

The last position represents a y power of the base (8). Example: 8y where y represents the last position.

Example

Octal Number − 125758

Calculating Decimal Equivalent −

Step	Octal Number	Decimal Number
Step 1	125758	((1 × 84) + (2 × 83) + (5 × 82) + (7 × 81) + (5 × 80))10
Step 2	125758	(4096 + 1024 + 320 + 56 + 5)10
Step 3	125758	550010

Note: 125758 is normally written as 12575 in octal.

Hexadecimal Number System

It uses 10 digits starting from 0,1,2,3,4,5,6,7,8,9 and 6 letters A, B, C, D, E, F.

These letters represent numbers as A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

It is also known as base 16 number system.

Here each position represents a power of the base (16). Example 161.

The last position represents a y power of the base (16). Example: 16y where y represents the last position.

Example −

Hexadecimal Number: 19FDA16

Calculating Decimal Equivalent −

Step	Hexadecimal Number	Decimal Number
Step 1	19FDA16	((1 × 164) + (9 × 163) + (F × 162) + (D × 161) + (A × 160))10
Step 2	19FDA16	((1 × 164) + (9 × 163) + (15 × 162) + (13 × 161) + (10 × 160))10
Step 3	19FDA16	(65536 + 36864 + 3840 + 208 + 10)10
Step 4	19FDA16	10645810

Note − 19FDA16 is normally written as 19FDA in hexa decimal.

Conversions:

There are many techniques which are used to convert numbers from one base to another. These are as follows −

Decimal to any other Base System

Any Base System to Decimal

Any Base System to Non-Decimal

Binary to Octal

Octal to Binary

Binary to Hexadecimal

Hexadecimal to Binary

Decimal to Any Base System

It includes the following steps:

Firstly, divide the decimal number which is to be converted by the value of its new base.

Then, after getting the remainder from the above step make it the rightmost digit (least significant digit) i.e., LSD of new base number.

Further divide the quotient by the new base.

Then record the remainder from the above step as the next digit (towards the left) of the new base number.

Repeat these steps and get remainders from right to left till the quotient becomes zero.

The last remainder obtained will be the Most Significant Digit (MSD) of the new base number.

For example −

Decimal Number: 2710

Calculating Binary Equivalent −

Step	Operation	Result	Remainder
Step 1	27 / 2	13	1
Step 2	13 / 2	6	1
Step 3	6 / 2	3	0
Step 4	3 / 2	1	1
Step 5	1 / 2	0	1

Hence, the remainders are arranged in the reverse order and we get:

Decimal Number − 2710 = Binary Number − 110112.

Any Base System to Decimal System

Here, the column (positional) value of each digit (this depends on the position of the digit and the base of the number system) is multiplied with the obtained column values of the digits in the corresponding columns.

The sum the products is then calculated which gives the total equivalent value in decimal.

For example:

Binary Number − 111102

Calculating Decimal Equivalent −

Step	Binary Number	Decimal Number
Step 1	111102	((1 × 24) + (1 × 23) + (1 × 22) + (1 × 21) + (0 × 20))10
Step 2	111102	(16 + 8 + 4 + 2 + 0)10
Step 3	111102	3010

Binary Number − 111102 = Decimal Number − 3010

Any Base System to Non-Decimal System

The original number is converted to its equivalent decimal number (base 10).

Then the decimal number so obtained is further converted to the new base number.

Example

Octal Number − 268

Calculating its Binary Equivalent −

Step 1 – Converting octal to Decimal

Step	Octal Number	Decimal Number
Step 1	268	((2 × 81) + (6 × 80))10
Step 2	268	(16 + 6 )10
Step 3	268	2210

Octal Number − 268 = Decimal Number − 2210

Step 2 − Converting Decimal to Binary

Step	Operation	Result	Remainder
Step 1	22 / 2	11	0
Step 2	11 / 2	5	1
Step 3	5 / 2	2	1
Step 4	2 / 2	1	0
Step 5	1 / 2	0	1

Decimal Number − 2210 = Binary Number − 101102

Octal Number − 268 = Binary Number − 101102

Binary to Octal

Dividing the binary digits into groups of three starting from right to left.

Converting each group of three binary digits into one octal digit.

For example:

Binary Number − 101012

Its Octal Equivalent −

Step	Binary Number	Octal Number
Step 1	101012	010 101
Step 2	101012	28 58
Step 3	101012	258

Binary Number − 101012 = Octal Number − 258

Octal to Binary

Converting each octal digit to a 3-digit binary number and they can be treated as decimal number for this conversion.

Then combining all the resulting binary groups into a single binary number.

For example:

Octal Number − 258

Its Binary Equivalent −

Step	Octal Number	Binary Number
Step 1	258	210 510
Step 2	258	0102 1012
Step 3	258	0101012

Octal Number − 258 = Binary Number − 101012

Binary to Hexadecimal

Dividing the binary digits into groups of four (starting from right to left).

Then converting each group of four binary digits into one hexadecimal number.

For example:

Binary Number − 101012

Its hexadecimal Equivalent −

Step	Binary Number	Hexadecimal Number
Step 1	101012	0001 0101
Step 2	101012	110 510
Step 3	101012	1516

Binary Number − 101012 = Hexadecimal Number − 1516

Hexadecimal to Binary

Converting each hexadecimal digit to a 4-digit binary number and they can be treated as decimal number.

Combining all the resulting binary groups into a single binary number.

For example:

Hexadecimal Number − 1516

Its Binary Equivalent −

Step	Hexadecimal Number	Binary Number
Step 1	1516	110 510
Step 2	1516	00012 01012
Step 3	1516	000101012

Hexadecimal Number − 1516 = Binary Number − 101012

Key takeaway

Conversion Table are provided here so that you can convert decimal to binary, binary to octal, octal to hexadecimal,a… | Computer coding, Decimals, Computer science

1.2 Arithmetic Operation using 1’s and 2s Compliments

Binary system complements:

Complements are used in order to simplify the subtraction operation and the logical manipulations can be done.

For each radix-r system there are two types of complements:

S.N.	Complement	Description
1	Radix Complement	It is referred to as the r's complement.
2	Diminished Radix Complement	It is referred to as the (r-1)'s complement.

The binary system has radix r = 2.

Therefore, the two types of complements for the binary system are known as 1's complement and 2's complement.

1's complement

Here, a number is obtained by changing all 1's to 0's and all 0's to 1's.

This is called as 1's complement.

For Example:

1's complement

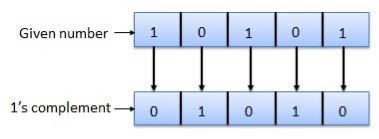
Fig.1: 1's complement

2's complement

It is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.

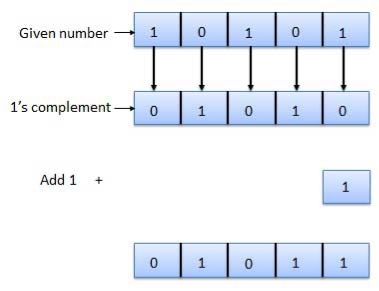
Hence, 2's complement = 1's complement + 1

For Example:

2's complement

Fig.2: 2's complement

Using 1’s complement:

Example1: Subtract 134 from 168.

Sol: 168-134 = 168 + (-134)

Binary representation of 168= 1010 1000

Binary representation of 134= 1000 0110

Binary representation of -134= 0111 1001

[Because 1’s complement represents the negative magnitude of a binary number]

168 + (-134) = 1010 1000 + 0111 1001 = 10010 0001

As a carry bit is present, 1 will be added to the result and it represents that the result is positive. 0010 0001 + 1 = 0010 0010

Decimal representation of 0010 0010 is 34.

168-134=34; hence the result is correct.

Example2: Subtract 168 from 134.

Sol: 134-168 = 134 + (-168)

Binary representation of 134= 1000 0110

Binary representation of 168= 1010 1000

Binary representation of -168= 0101 0111

[Because 1’s complement represents the negative magnitude of a binary number]

134 + (-168) = 1000 0110 + 0101 0111=1101 1101

As a carry bit is absent, 1’s complement of this value will be the final result and absence of carry bit represents that the result is negative.

1’s complement of 1101 1101 = 0010 0010

Decimal representation of 0010 0010 is 34.

As carry bit is absent the result is negative i.e., -34 134 -168= -34; hence the result is correct.

Using 2’s complement

Example 1: Subtract 96 from 118.

Sol: 118-96 = 118 + (-96)

Binary representation of 118= 0111 0110

Binary representation of 96= 0110 0000

Here 2’s complement represents the negative magnitude of a binary number.

Hence 2’s complement of 96 represents -96.

So -96= 1001 1111 118 + (-96) = 0111 0110 + 1001 1111=10001 0101

As a carry bit is present, 1 will be added to the result and presents of carry bit represents that the result is positive. 0001 0101+ 1= 0001 0110

Decimal representation of 0001 0110 is 22.

As carry bit is present the result is positive.

Example 2: Subtract 118 from 96.

Sol: 118-96 = 96 + (-118)

Binary representation of 96= 0110 0000

Binary representation of 118= 0111 0110

Here 2’s complement represents the negative magnitude of a binary number.

Hence 2’s complement of 118 represents -118.

So -118= 1000 1010 96 + (-118) = 0110 0000 + 1000 1010 1110 1010

As a carry bit is absent, 2’s complement of this value will be the final result and absence of carry bit represents that the result is negative.

2’s complement of 1110 1010 = 0001 0110

Decimal representation of 0001 0110 is 34. As carry bit is absent the result is negative i.e., -34

Key takeaway

2's complement

It is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.

Hence, 2's complement = 1's complement + 1

1.3 Signed Binary and Floating-Point Number

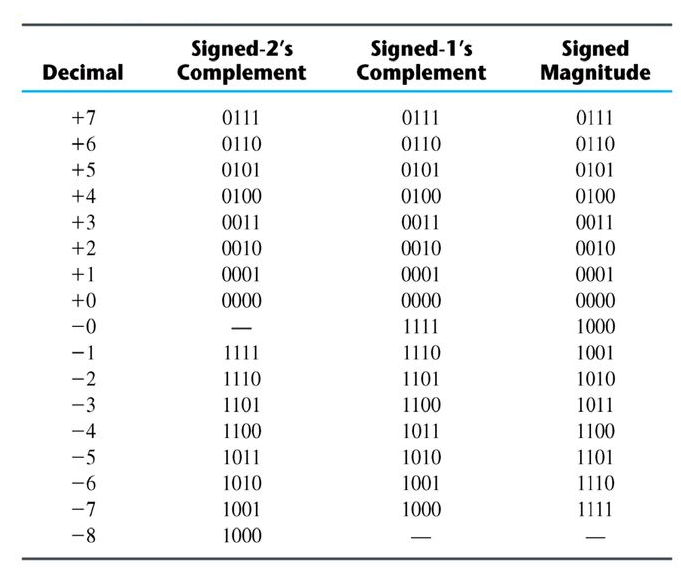
Signed Binary:

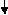For a binary number the most significant bit (MSB) denotes the signed bit. For example, +9 using 8-bits is denoted as 10001001

MSB

The table below shows all the signed four-bit binary numbers.

Binary Addition

If both the signed magnitude numbers have same sign. We add both of them and the result is given common sign.

If both the numbers have different signs, the smaller number is subtracted from the larger and the result is given the sign of larger number.

Binary Addition in 2’s compliment form:

Both numbers are added with their sign bits and the carry bit is discarded.

Binary Subtraction in 2’s compliment form:

We first find the 2’s compliment of the subtrahend and add with minuend. If carry is found at the signed-bit then it is discarded.

For example: (-6) -(-13) = (11111010 – 11110011)

= (11111010+00001101)

= (00000111) = +7

Floating Point Numbers

This is the most common method for representation of real numbers on computers. To represent floating point numbers IEEE has set a standard. IEEE 754 numbers have basic components as listed below:

The Sign of Mantissa –This is as simple as the name. 0 represents a positive number while 1 represents a negative number.

The exponent –The exponent field needs to represent both positive and negative exponents. A bias is added to the actual exponent in order to get the stored exponent.

The Normalised Mantissa –The mantissa is part of a number in scientific notation or a floating-point number, consisting of its significant digits. Here we have only 2 digits, i.e., 0 and 1. So a normalised mantissa is one with only one 1 to the left of the decimal.

We can summarise the above as:

The exponent base is two. The exponent field contains 127 plus the true exponent for single-precision, or 1023 plus the true exponent for double precision. The first bit of the mantissa is typically assumed to be 1.

On the basis of above three components IEEE 754 can be categorised as

a) Single Precision: It is 8-bit exponent field.

The number ranges which the single precision floating point number cannot represent are:

i) Negative numbers less than −(2−2−23) × 2127

ii) Negative numbers greater than −2−149

iii) Zero

iv) Positive numbers less than 2−149

v) Positive numbers greater than (2−2−23) × 2127

b) Double Precision

Few numbers which are still not defined in this standard are:

i) Denormalized: If the exponent is 0 the value is a denormalized number.

Key takeaway

The exponent field contains 127 plus the true exponent for single-precision, or 1023 plus the true exponent for double precision. The first bit of the mantissa is typically assumed to be 1.

1.4 Representation Introduction to Binary codes and their applications

In coding, when alpha-numeric characters or words are represented by a specific group of symbols, it is said that it is being coded.

The group of symbols is known as a code.

The digital data can be represented, stored and transmitted as group of binary bits.

This group is called as binary code.

It is represented by the number as well as alphanumeric character.

Advantages of Binary Code

They are used in computer applications.

They are suitable for digital communications.

They make the analysis and designing of digital circuits easy.

Implementation becomes very easy since only 0 & 1 are being used.

Classification of binary codes

The codes are broadly classified as:

Weighted Codes

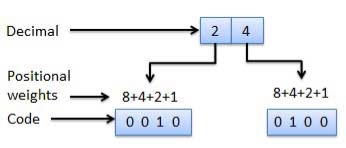
Non-Weighted Codes

Binary Coded Decimal Code

Alphanumeric Codes

Error Detecting Codes

Error Correcting Codes

Weighted Codes

These codes obey the positional weight principle.

Here each position represents a specific weight.

Several systems are used to express the decimal digits 0 through 9.

Here, each decimal digit is represented by a set of four bits.

Weighted Code

Fig.3: Weighted codes (Ref. 1)

Non-Weighted Codes

Here, the positional weights are not assigned.

Example: Excess-3 code and Gray code.

1.Excess-3 code

It is also known as XS-3 code.

It is a non-weighted code used to express decimal numbers.

They are derived from the 8421 BCD code words adding (0011)2 or (3)10 to each code word in 8421.

The excess-3 codes are obtained as−

Excess-3 code

Example

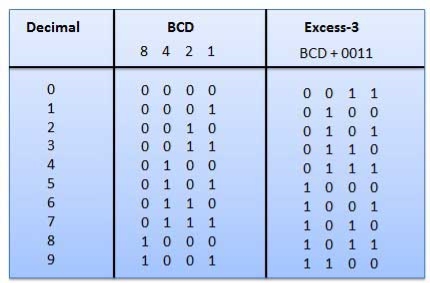
BCD to Excess-3 code

Fig.4: BCD to XS 3 conversion (Ref. 1)

2.Gray Code

It is the non-weighted code and is not an arithmetic code.

This means that there are no specific weights assigned to the bit position.

Here only one bit will change every time the decimal number is incremented.

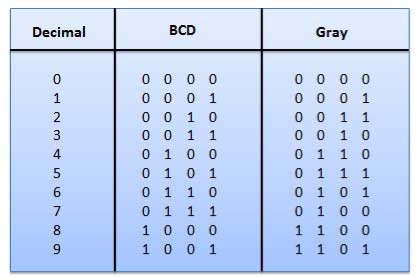
The gray code is also known as a unit distance code as only one-bit changes at a time.

The gray code is a type of cyclic code.

It cannot be used for all arithmetic operation.

Gray code

Fig.5: Gray codes (Ref. 1)

Application of Gray code

They are used in the shaft position encoders.

This encoder produces a code word which represents the angular position of the shaft.

3. Binary Coded Decimal (BCD) code

Here each decimal digit is represented by a 4-bit binary number.

It’s a way to express each of the decimal digits with a binary code.

Therefore, by four bits we can represent sixteen numbers (0000 to 1111).

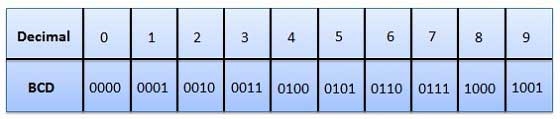
But in BCD code only first ten of these numbers are used (0000 to 1001) and rest are invalid.

BCD code

Fig.6: BCD codes (Ref. 1)

Advantages of BCD Codes

It is very similar to decimal system.

We have to remember binary equivalent of 0 to 9 only.

Disadvantages of BCD Codes

The addition and subtraction of BCD number system have different rules.

The BCD arithmetic is more complicated.

BCD code requires more number of bits than binary code to represent the decimal number.

Hence is less efficient than binary.

4. Alphanumeric codes

A binary digit or bit can be represented by two symbols as '0' or '1'.

This is not sufficient for communication between two computers as we need many more symbols for communication.

These symbols are representing 26 alphabetic characters with capital and small letters, numbers from 0 to 9, punctuation marks and other symbols.

These alphanumeric codes represent numbers and alphabetic characters.

Most of them also represent other characters like symbol and various instructions necessary for conveying information.

The code at least represents 10 digits and 26 letters of alphabet i.e., total 36 items.

The following three types of alphanumeric codes are commonly used for the data representation.

American Standard Code for Information Interchange (ASCII).

Extended Binary Coded Decimal Interchange Code (EBCDIC).

Five-bit Baudot Code.

ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code.

ASCII code is used worldwide while EBCDIC is primarily used in large IBM computers.

5.Error Codes

There technique is available to detect and correct data during data transmission.

Error Code	Description
Error Detection and Correction	Error detection and correction code techniques

Key takeaway

In BCD code only first ten of these numbers are used (0000 to 1001) and rest are invalid.

ASCII code is a 7-bit code whereas EBCDIC is an 8-bit code.

1.5 Revision Boolean Algebra and Logic Gates: Boolean algebra and identities

It deals with binary numbers & variables.

Therefore, also known as Binary Algebra or logical Algebra.

A mathematician named as George Boole had developed this algebra in 1854.

The variables that are used in this algebra are known as Boolean variables.

Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.

Postulates and Basic Laws of Boolean Algebra

Here, the Boolean postulates and basic laws that are used are given underneath.

Boolean Postulates

Considering the binary numbers 0 and 1, boolean variable (x) and its complement (x’).

They know as literal.

The possible logical OR operations are:

x + 0 = x

x + 1 = 1

x + x = x

x + x’ = 1

Similarly, the possible logical AND operations are:

x.1 = x

x.0 = 0

x.x = x

x.x’ = 0

These are the simple Boolean postulates and verification can be done by substituting the Boolean variable with ‘0’ or ‘1’.

Basic Laws of Boolean Algebra

The three basic laws of Boolean Algebra are:

Commutative law

Associative law

Distributive law

Commutative Law

The logical operation carried between two Boolean variables when gives the same result irrespective of the order the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below

x + y = y + x

x.y = y.x

The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.

Commutative law holds good for logical OR & logical AND operations.

Associative Law

If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:

x + (y + z) = (x + y) + z

x. (y.z) = (x.y). z

Associative law holds good for logical OR & logical AND operations.

Distributive Law

If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are:

x. (y + z) = x.y + x.z

x + (y.z) = (x + y). (x + z)

Distributive law holds good for logical OR and logical AND operations.

These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.

Theorems of Boolean Algebra

The following theorems are used in Boolean algebra.

Duality theorem
De Morgan’s theorem

Duality Theorem

It states that “The dual of the Boolean function is obtained by interchanging the logical AND operator with logical OR operator and zeros with ones”.

For every Boolean function, there is a Dual function.

Let us make the Boolean equations (relations) of Boolean postulates and basic laws into two groups. The following table shows these two groups.

Group1	Group2
x + 0 = x	x.1 = x
x + 1 = 1	x.0 = 0
x + x = x	x.x = x
x + x’ = 1	x.x’ = 0
x + y = y + x	x.y = y.x
x + (y + z) = (x + y) + z	x. (y.z) = (x.y). z
x. (y + z) = x.y + x. z	x + (y.z) = (x + y). (x + z)

Every row comprises of two Boolean equations and they are dual to one other.

We can also verify the Boolean equations of Group1 and 2 by using duality theorem.

De Morgan’s Theorem

It is useful in finding the complement of Boolean function.

It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.

It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’. y’

The dual of the above Boolean function is

(x.y)’ = x’ + y’

Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.

Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

Simplification of Boolean Functions

Numerical

Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1

Given

f = p’qr + pq’r + pqr’ +pqr.

In first and second term r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive law we get,

⇒ f = (p’q + pq’) r + pq (r’ + r)

The terms present in first parenthesis can be simplified by using Ex-OR operation.

The terms present in second parenthesis is equal to ‘1’ using Boolean postulate we get

⇒ f = (p ⊕q) r + pq (1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q) r + pq

Therefore, the simplified Boolean function is f = (p⊕q) r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence, we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr (p’ + p) + pr (q’ + q) + pq (r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification.

⇒ f = qr (1) + pr (1) + pq (1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence, we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are same. As per requirement, we can choose one of them.

Numerical

Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using DeMorgan’s theorem, (x + y)’ = x’. y’ we get

⇒ f’ = (p’q)’. (pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}. {p’ + (q’)’}

Then by using, (x’)’=x we get

⇒ f’ = {p + q’}. {p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

Key takeaways

1.6 Complete Logic set

Digital Electronics logic gates AND, OR, NOT, NAND, NOR, XOR, XNOR explain in Urdu/Hindi | Logic, Nand gate, What is logic

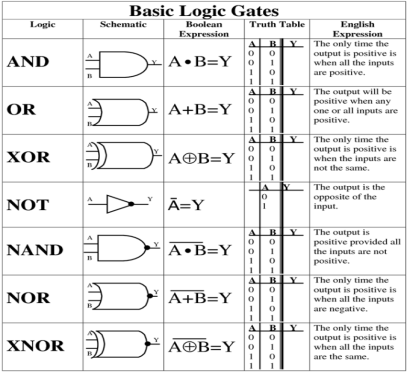
If any digital circuit can be built from a set of gates, that set is said to be functionally complete

Functionally complete sets of gates: AND, OR, & NOT, NAND, NOR

To show a set of gates is functionally complete, we must show that you can construct AND, OR and NOT functions

The NAND gate is functionally complete

We can build any digital logic circuit out of all NAND gates

Same holds true for the NOR gate and the multiplexer

The XOR & XNOR are not functionally complete.

1.7 Logic gates and truth tables

Digital electronic circuits operate at two logic levels namely Logic Low and Logic High.

The Logic Low is represented with ‘0’and Logic High is represented with ‘1’.

The basic digital electronic circuit which has one or more inputs and single output is known as Logic gate.

These Logic gates are known as the building blocks of any digital system. They can be classified as:

Basic gates

Universal gates

Special gates

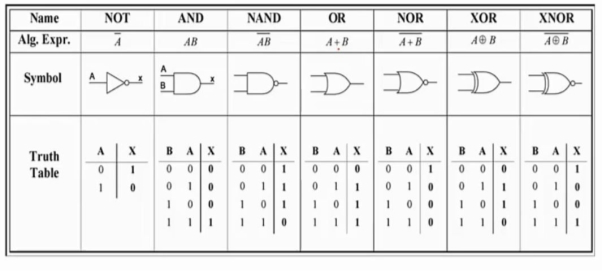
Basic Gates

The basic gates are namely AND gate, OR gate & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

A	B	Y = A. B
0	0	0
0	1	0
1	0	0
1	1	1

Here A, B are the inputs and Y is the output of two input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B and one output, Y.

And Gate

Fig.7: AND gate (ref. 1)

OR gate

It is a digital circuit which has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of 2-input OR gate is:

A	B	Y = A + B
0	0	0
0	1	1
1	0	1
1	1	1

Here A, B are the inputs and Y is the output of two input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B and one output, Y.

Fig.8: OR gate (ref. 1)

NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called as an inverter.

The truth table of NOT gate is:

A	Y = A’
0	1
1	0

Here A and Y are the corresponding input and output of NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

Fig.9: NOT gate (ref. 1)

1.8 Universal logic gates

NAND & NOR gates are known as universal gates.

We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit which has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of 2-input NAND gate is:

A	B	Y = (A.B)’
0	0	1
0	1	1
1	0	1
1	1	0

Here A, B are the inputs and Y is the output of two input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the inputs is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

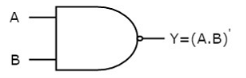
Fig.10: NAND gate (ref. 1)

NAND gate works same as AND gate followed by an inverter.

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

A	B	Y = (A+B)’
0	0	1
0	1	0
1	0	0
1	1	0

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If any one of the inputs is ‘1’, then the output is ‘0’. This is exactly opposite to two input OR gate operation.

The symbol of NOR gate is:

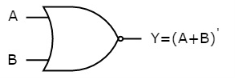
Fig.11: NAND gate (ref. 1)

NOR gate works exactly same as that of OR gate followed by an inverter.

Special Gates

Ex-OR gate

It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

A	B	Y = A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

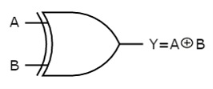
Fig.12: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

Ex-NOR gate

It stands for Exclusive-NOR gate. Its function is same as that of NOR gate except when the inputs having even number of ones.

The truth table of 2-input Ex-NOR gate is:

A	B	Y = A⊙B
0	0	1
0	1	0
1	0	0
1	1	1

Here A, B are the inputs and Y is the output. It is same as Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0, when both the inputs are one.

Hence the output of Ex-NOR gate is ‘1’, when both inputs are same and 0, when both the inputs are different.

The symbol of Ex-NOR gate is:

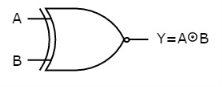
Fig.13: XNOR gate (ref. 1)

It is similar to NOR gate except for few combination(s) of inputs. Here the output is ‘1’, when even number of 1 is present at the inputs. Hence is also called as an even function.

Key takeaway

Chapter 3-Logic gates and Logic Circuits | IGCSE Computer Science

1.9 Algebraic Reduction and realization using logic gates

Boolean Expression for a Logic Circuit To derive the Boolean expression for a given logic circuit, begin at the leftmost inputs and work toward the final output, writing the expression for each gate. For the example circuit in Fig, the Boolean expression is determined as follows:

 The expression for the left-most AND gate with inputs C and D is CD.

 The output of the left-most AND gate is one of the inputs to the OR gate and B is the other input. Therefore, the expression for the OR gate is B + CD.

 The output of the OR gate is one of the inputs to the right-most AND gate and A is the other input. Therefore, the expression for this AND gate is A (B + CD), which is the final output expression for the entire circuit.

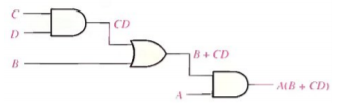
Fig 14 Logic Circuit showing the Boolean Expression for the output

Examples

Q1) Using Boolean algebra techniques, simplify this expression: AB + A (B + C) + B (B + C)

Solution

Step 1: Apply the distributive law to the second and third terms in the expression, as follows: AB + AB + AC + BB + BC

Step 2: Apply rule 7 (BB = B) to the fourth term. AB + AB + AC + B + BC

Step 3: Apply rule 5 (AB + AB = AB) to the first two terms. AB + AC + B + BC

Step 4: Apply rule 10 (B + BC = B) to the last two terms. AB + AC + B

Step 5: Apply rule 10 (AB + B = B) to the first and third terms. B+AC At this point the expression is simplified as much as possible.

Fig 15 Implementation using gates

Q2) Design a logic circuit that has three inputs, A, B, and C, and whose output will be HIGH only when a majority of the inputs are HIGH.

Solution Step 1. Set up the truth table. On the basis of the problem statement, the output x should be 1 whenever two or more inputs are 1; for all other cases, the output should be 0

Fig 16 Truth Table with AND terms

Step 2. Write the AND term for each case where the output is a 1. There are four such cases. The AND terms are shown next to the truth table. Again, note that each AND term contains each input variable in either inverted or noninverted form.

Step 3. Write the sum-of-products expression for the output. x = 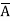BC + A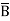C + AB 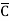+ ABC

Step 4. Simplify the output expression.

This expression can be simplified in several ways. Perhaps the quickest way is to realize that the last term ABC has two variables in common with each of the other terms. Thus, we can use the ABC term to pair with each of the other terms. The expression is rewritten with the ABC term occurring three times:

x = 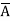BC + A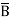C + AB 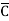+ ABC + ABC + ABC

Factoring the appropriate pairs of terms, we have

x = BC (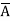 + A) + AC ( 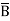+ B) + AB ( 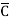+ C) Each term in parentheses is equal to 1, so we have x = BC + AC + AB

Step 5. Implement the circuit for the final expression. This expression is implemented in Figure. Since the expression is in SOP form, the circuit consists of a group of AND gates working into a single OR gate.

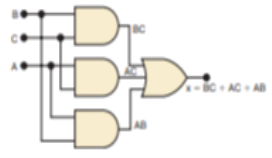
Fig 17 Implementation using gates

References:

Digital Design, 3rd Edition, Moris M. Mano, Pearson Education.

Fundamentals of digital circuits, 8th edition, A. Anand Kumar, PHI

Digital Fundamentals, 5th Edition, T.L. Floyd and R.P. Jain, Pearson Education, New Delhi.

Digital Electronics, G. K. Kharate, Oxford University Press.

Digital Systems – Principles and Applications, 10th Edition, Ronald J. Tocci, Neal S. Widemer and Gregory L. Moss, Pearson Education.

A First Course in Digital System Design: An Integrated Approach, India Edition, John P. Uyemura, PWS Publishing Company, a division of Thomson Learning Inc.

Digital Systems – Principles and Applications, 10th Edition, Ronald J. Tocci, Neal S. Widemer and Gregory L. Moss, Pearson Education.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined