2.1 Combinational Logic Design Specifying the Problem | unit 2 combinational logic design

DSD

Combinational Logic Design

2.1 Combinational Logic Design: Specifying the Problem

A Combinational circuit is a circuit in which we combine the different gates. For example, encoder, decoder, multiplexer, demultiplexer etc. Some of the characteristics are as follows −

The output of combinational circuit depends only on the levels present at input terminals at any instant of time.

It does not use any memory element. Therefore, the previous state of input does not have any effect on the present state of the circuit.

It can have n number of inputs and m number of outputs.

Block diagram

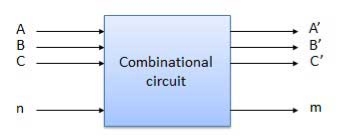
Block Diagram of combinational circuit

Fig: Combinational circuit (ref.2)

Key takeaway

The output of combinational circuit depends only on the levels present at input terminals at any instant of time.

It does not use any memory element

2.2 Canonical Logic Forms

Four product combinations are obtained by combining two variables x and y with logical AND operation. They are called as min terms or standard product terms. The min terms are given as x’y’, x’y, xy’ and xy.

In the same way, four Boolean sum terms are obtained by combining two variables x and y with logical OR operation. They are called as Max terms or standard sum terms. The Max terms are given as x + y, x + y’, x’ + y and x’ + y’.

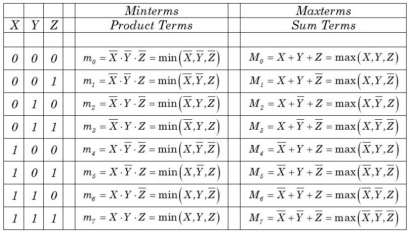
The following table represents the min terms and MAX terms for 2 variables.

x	y	Min terms	Max terms
0	0	m0=x’y’	M0=x + y
0	1	m1=x’y	M1=x + y’
1	0	m2=xy’	M2=x’ + y
1	1	m3=xy	M3=x’ + y’

If the binary variable is ‘0’, then it is represented as complement of variable in min term and as the variable itself in Max term.

Similarly, if it is ‘1’, then it is represented as complement of variable in Max term and as the variable itself in min term.

From the above table, we can easily notice that min terms and Max terms are complement of each other.

If there are ‘n’ Boolean variables, then there will be 2n min terms and 2n Max terms.

Canonical SoP and PoS forms

A truth table comprises of a set of inputs and output(s).

If there are ‘n’ input variables, then there shall be 2n possible combinations comprising of zeros and ones.

So, the value of every output variable depends on the combination of input variables.

Hence, each output variable has ‘1’ for some combination and ‘0’ for other combination of input variables.

Therefore, we can express each output variable in two ways.

Canonical SoP form

Canonical PoS form

Canonical SoP form

It means Canonical Sum of Products form.

In this, each product term contains all literals.

So that these product terms are nothing but the min terms.

Hence is also known as sum of min terms form.

Firstly, identification of the min terms is done and then the logical OR of those min terms is taken in order to get the Boolean expression (function) corresponding to that output variable.

This Boolean function will be in sum of min terms form.

Then following the same procedure for other output variables too.

Example

Considering the following truth table.

Inputs		Output
P	q	r	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Here, the output (f) is ‘1’ for only four combinations of inputs.

The corresponding min terms are given as p’qr, pq’r, pqr’, pqr.

By doing logical OR, we get the Boolean function of output (f).

Hence, the Boolean function of output is,

f = p’qr + pq’r + pqr’ + pqr.

This is the desired canonical SoP form of output, f.

It can also be represented as:

f=m3+m5+m6+m7f=m3+m5+m6+m7

f=∑m (3,5,6,7) f=∑m (3,5,6,7)

First, we represented the function as sum of respective min terms and then, the symbol for summation of those min terms is used.

Canonical PoS form

It means Canonical Product of Sums form.

Here In this form, each sum term contains all literals.

These sum terms are the Max terms.

Hence, canonical PoS form is also known as product of Max terms form.

Identification of the Max terms for which the output variable is zero is done and then the logical AND of those Max terms is done in order to get the Boolean expression corresponding to that output variable.

This Boolean function is in the form of product of Max terms.

Following the same procedure for other output variables too.

Standard SoP and PoS forms

Standard SoP form

It stands for Standard Sum of Products form.

In this, each product term need not contain all literals.

So, the product terms can or cannot be the min terms.

Therefore, it is therefore the simplified form of canonical SoP form.

Standard SoP of output variable can be obtained by two steps.

Getting the canonical SoP form of output variable

Simplification the above Boolean function.

The same procedure is followed for other output variables too, if there is more than one output variable.

Standard PoS form

It stands for Standard Product of Sum form.

Here, each sum term need not contain all literals.

So, the sum terms can or cannot be the Max terms.

Therefore, it is the desired simplified form of canonical PoS form.

Standard PoS form of output variable is obtained by two steps.

Getting the canonical PoS form of output variable

Simplification of the above Boolean function.

The same procedure is followed for other output variables too.

Key takeaway

Canonical and Standard Form - GeeksforGeeks

2.3 Extracting Canonical Forms

Numerical

Q1) Convert the Boolean function into Standard SoP form.

f = p’qr + pq’r + pqr’ + pqr

Solution:

Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.

⇒ f = qr (p’ + p) + pr (q’ + q) + pq (r’ + r)

Step 3 – Then Using Boolean postulate, x + x’ = 1 we get

⇒ f = qr (1) + pr (1) + pq (1)

Step 4 – hence using Boolean postulate, x.1 = x we get

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

This is the required Boolean function.

Q2) Convert the Boolean function into Standard PoS form.

f = (p + q + r). (p + q + r’). (p + q’ + r). (p’ + q + r)

Solution:

Step 1 – By using the Boolean postulate, x.x = x and writing the first term p+q+r two more times we get

⇒ f = (p + q + r). (p + q + r). (p + q + r). (p + q + r’). (p +q’ + r). (p’ + q + r)

Step 2 – Now by using Distributive law, x + (y.z) = (x + y). (x + z) for 1st and 4thparenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.

⇒ f = (p + q + rr’). (p + r + qq’). (q + r + pp’)

Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.

⇒ f = (p + q + 0). (p + r + 0). (q + r + 0)

Step 4 − Using Boolean postulate, x + 0 = x we get

⇒ f = (p + q). (p + r). (q + r)

⇒ f = (p + q). (q + r). (p + r)

This is the simplified Boolean function.

Hence, both Standard SoP and Standard PoS forms are Dual to one another.

2.4 EX-OR Equivalence Operations, Logic Array

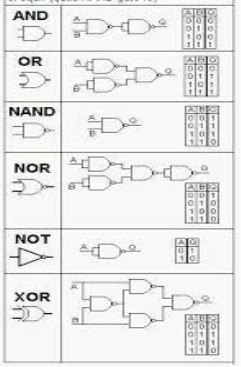
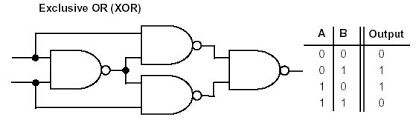
It stands for Exclusive-OR gate. Its function varies when the inputs have even number of ones.

The truth table of 2-input Ex-OR gate is:

A	B	Y = A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

The symbol of Ex-OR gate is as follows:

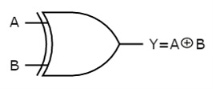
Fig: XOR gate (ref. 1)

It is similar to that of OR gate with an exception for few combination(s) of inputs. Hence, the output is also known as an odd function.

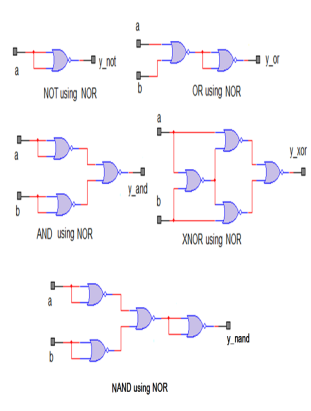
Ex-OR Function Realisation using NAND gates

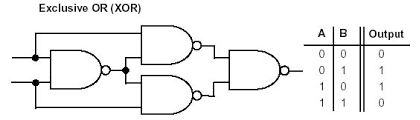
GATE IT 2004 | Question: 8 - GATE Overflow

Fig. Realisation using NAND Gates

Exclusive-OR Gates are used mainly to build circuits that perform arithmetic operations and calculations especially Adders and Half-Adders as they can provide a “carry-bit” function or as a controlled inverter, where one input passes the binary data and the other input is supplied with a control signal.

Key takeaway

The output of Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero, when both inputs are same.

2.5 K-Maps: Two, Three and Four variable K-maps

Karnaugh introduced a method for simplification of Boolean functions in a very easy way.

This method is known as Karnaugh map method or K-map method.

It is a graphical method, which comprises of 2n cells for ‘n’ variables.

Here, the adjacent cells vary only in single bit position.

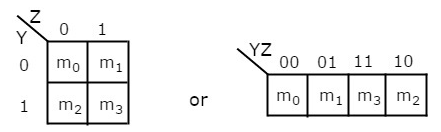
K-Maps for 2 to 5 Variables

It is the most suitable method for minimizing Boolean functions of 2 variables to 5 variables.

2 Variable K-Map

It has 4 number of cells since the number of variables is two.

The 2 variable K-Map is:

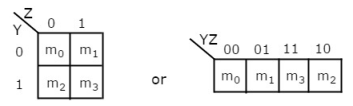
Fig: 2 variable K-Map (ref. 1)

The only way to group 4 adjacent min terms.

The possible combinations are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.

3 Variable K-Map

It has 8 number of cells since the number of variables is 3.

The 3 variable K-Map is:

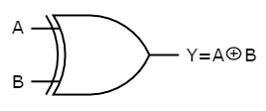
Fig: 3 variable K-Map

The only way to group 8 adjacent min terms.

The possible are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.

The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.

If x=0, then 3 variable K-map becomes 2 variable K-map.

4 Variable K-Map

It has 16 number of cells since the number of variables is 4.

The 4 variable K-Map is:

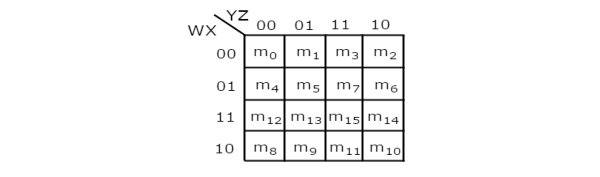
Fig: 4 variable K-Map

The only way to group 8 adjacent min terms.

Let R1, R2, R3 and R4 represents the min terms of first row, second row, third row and fourth row respectively.

Similarly, C1, C2, C3 and C4 represents the min terms of first column, second column, third column and fourth column respectively.

The possible combinations are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.

If w=0, then 4 variable K-map becomes 3 variable K-map.

Rules for simplifying K-maps:

Selecting K-map on the basis of number of variables present in the Boolean function.

If the Boolean function is in Max terms form, then place the zeroes at respective Max term cells in the K-map.

If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.

The maximum possibilities of grouping are checked for adjacent zeroes.

It should be of powers of two.

Starting from highest power of two and to the least power of two.

Highest power is equivalent to the number of variables considered in K-map and least power is zero.

Each group will give either a literal or one sum term.

It is known as prime implicant.

The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.

The simplified Boolean function contains all essential prime implicants and only the required prime implicants.

Key takeaway

The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.

If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.

Numerical

Simplify f (X, Y, Z) =∏M (0,1,2,4) f (X, Y, Z) =∏M (0,1,2,4) using K-map.

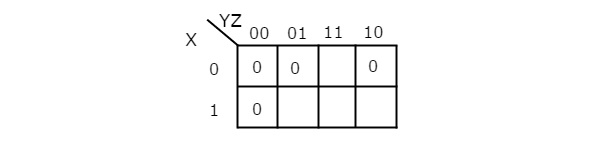
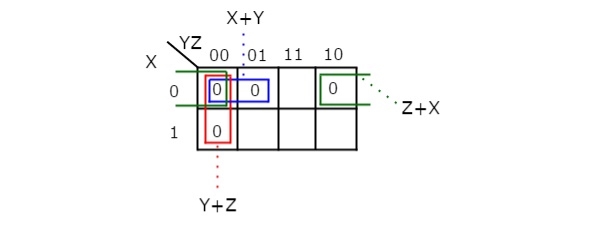
Prime Implicants ungrouped

Therefore, the simplified Boolean function is

f = (X + Y). (Y + Z). (Z + X)

Simplify:

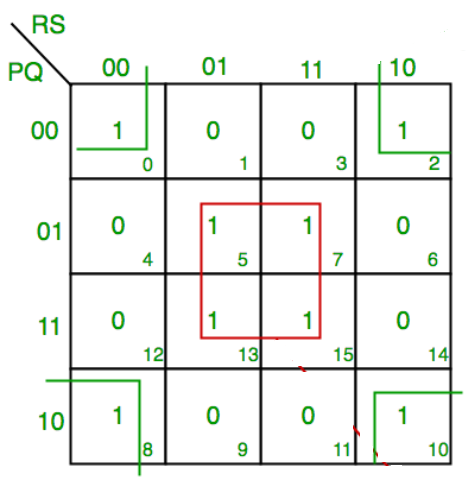
F (P, Q, R, S) =∑ (0,2,5,7,8,10,13,15)

F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS

F = P’Q’S’ + PQ’S’ + QS

F = Q’S’ +QS

Simplify:

F (A, B, C) =π (0,3,6,7)

F = A’BC +ABC +A’B’C’ +ABC’

F = BC + C’ (A’B’ + AB)

2.6 NAND and NOR Logic Implementations.

Any logic function can be implemented using NAND gates.

For this, the logic function has to be written in Sum of Product (SOP) form.

Consider the following SOP expression F = W.X.Y + X.Y.Z + Y.Z.W

The above expression can be implemented with three AND gates in first stage and one OR gate in second stage as shown in figure.

Fig: Implementation of F = W.X.Y + X.Y.Z + Y.Z.W

If bubbles are introduced at AND gates output and OR gates input (the same for NOR gates), the above circuit becomes.

Fig: Implementation of F = W.X.Y + X.Y.Z + Y.Z.W

Now replacing OR gate with input bubble with the NAND gate we have

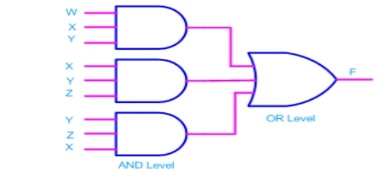
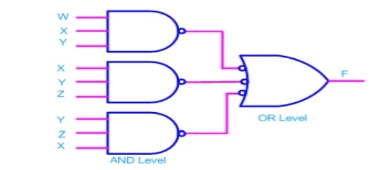
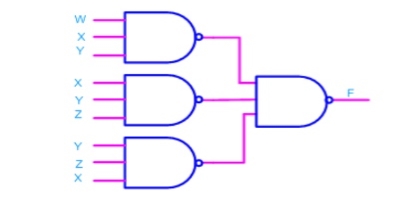
Fig: Implementation of F = W.X.Y + X.Y.Z + Y.Z.W

Realization of logic gates using NAND gates

Implementing an inverter using NAND gate

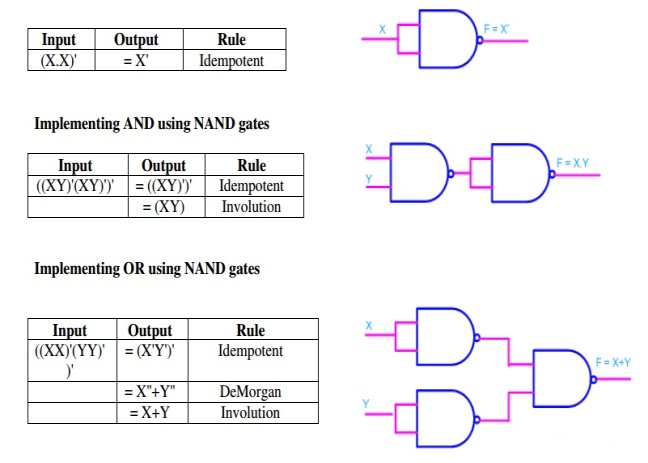
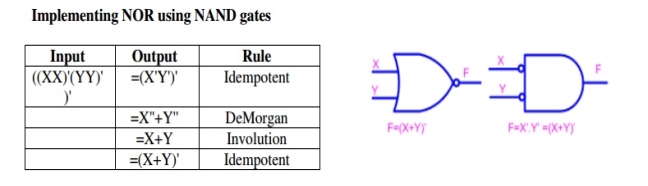
Fig: Implementation of basic gates using NAND gate

Realization of logic function using NOR gates

Any logic function can be implemented using NOR gates.

For this, the logic function has to be written in Product of Sum (POS) form

Consider the following POS expression F = (X+Y). (Y+Z)

It can be implemented with three OR gates in first stage and one AND gate in second stage

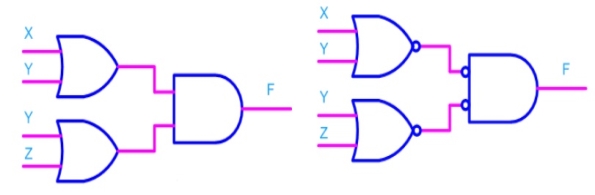
Fig: Implementation of F = (X+Y). (Y+Z)

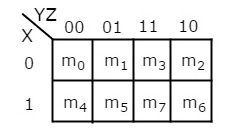
If bubbles are introduced at the output of the OR gates and the inputs of AND gate, the above circuit comes out to be the next figure.

Now replacing AND gate with input bubble with the NOR gate and we have circuit which is completely implemented with just NOR gates.

Fig: Implementation of F = (X+Y). (Y+Z)

Implementing logic gates using NOR gate

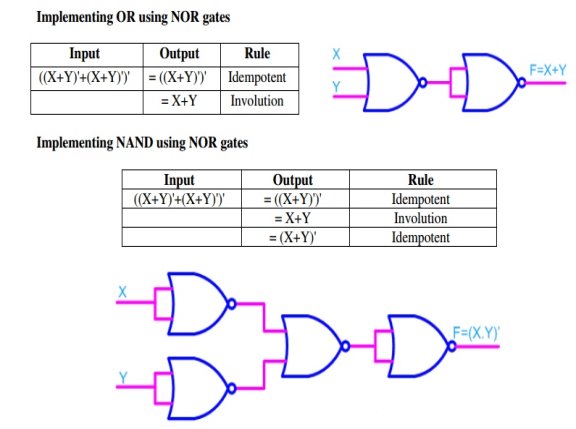
Fig: Implementation of Or and NAND gate using NOR gate

Key takeaway

How would you prove the universality of NAND gates and NOR gates? - Quora VHDL Tutorial – 8: NOR gate as a universal gate

2.7 Logic Components: Concept of Digital Components

A digital circuit whose outputs depend solely on the present combination of the circuit inputs’ values. Built out of simple components: switches and gates.

Electronic switches are the basis of binary digital circuits – Electrical terminology

• Voltage: Difference in electric potential between two points Analogous to water pressure

• Current: Flow of charged particles – Analogous to water flow

• Resistance: Tendency of wire to resist current flow – Analogous to water pipe diameter V I * R (Ohm’s Law)

A switch has three parts – Source input, and output

• Current wants to flow from source input to output

– Control input

• Voltage that controls whether that current can flow.

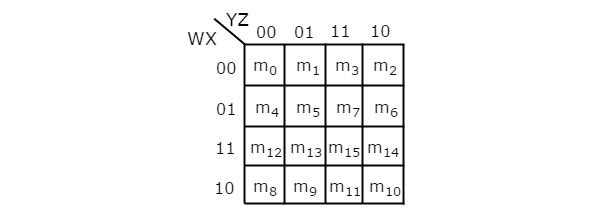
Fig: Switch

Integrated Circuits or IC’s as they are more commonly called, can be grouped together into families according to the number of transistors or “gates” that they contain.

Integrated circuits are categorised according to the number of logic gates or the complexity of the circuits within a single chip with the general classification for the number of individual gates given as:

Classification of Integrated Circuits

Small Scale Integration or (SSI) – Contain up to 10 transistors or a few gates within a single package such as AND, OR, NOT gates.

Medium Scale Integration or (MSI) – between 10 and 100 transistors or tens of gates within a single package and perform digital operations such as adders, decoders, counters, flip-flops and multiplexers.

Large Scale Integration or (LSI) – between 100 and 1,000 transistors or hundreds of gates and perform specific digital operations such as I/O chips, memory, arithmetic and logic units.

Very-Large Scale Integration or (VLSI) – between 1,000 and 10,000 transistors or thousands of gates and perform computational operations such as processors, large memory arrays and programmable logic devices.

Super-Large Scale Integration or (SLSI) – between 10,000 and 100,000 transistors within a single package and perform computational operations such as microprocessor chips, micro-controllers, basic PICs and calculators.

Ultra-Large Scale Integration or (ULSI) – more than 1 million transistors – the big boys that are used in computers CPUs, GPUs, video processors, micro-controllers, FPGAs and complex PICs.

2.8 Binary Adders, Subtraction and Multiplication

Half Adder

It is a combinational circuit which has two inputs and two outputs.

It is designed to add two single bit binary number A and B.

It has two outputs carry and sum.

Block diagram

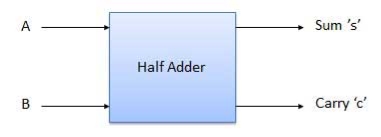
Block Diagram of Half Adder

Fig: Half adder (ref. 2)

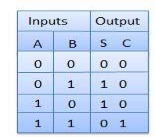
Truth Table

Half Adder Truth Table

Circuit Diagram

Half Adder Circuit Diagram

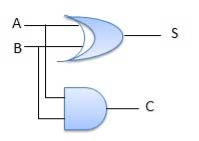
Fig: Half adder (ref. 2)

B. Full Adder

It is developed to overcome the drawback of Half Adder circuit.

It can add two one-bit numbers A and B and a carry C.

It is a three input and two output combinational circuit.

Block diagram

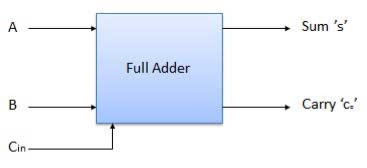
Block Diagram of Full Adder

Fig: Full adder (ref. 2)

Truth Table

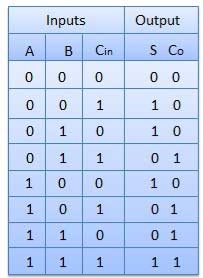
Full Adder Truth Table

Circuit Diagram

Full Adder Circuit Diagram

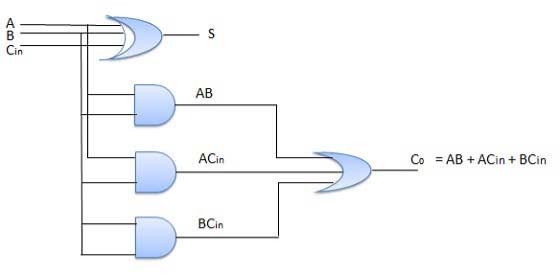
Fig: Full adder (ref. 2)

C. N-Bit Parallel Adder

The Full Adder adds only two single digit binary number along with a carry input.

But practically addition of binary numbers needs to be done which are much longer than just one bit.

To add the two n-bit binary numbers we use the n-bit parallel adder.

This adder uses many full adders in cascade.

The carry output of the previous full adder is given to carry input of the next full adder.

4 Bit Parallel Adder

Here, A0 and B0 represent the LSB of the four-bit words A and B.

Hence Adder-0 is the lowest stage.

Cin is considered 0.

The rest of the connections are same as that of n-bit parallel adder.

It is a very common logic circuit.

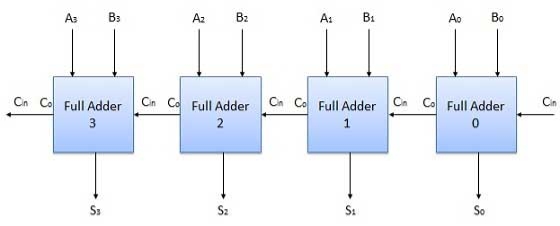
Block Diagram of Four bit Adder

Fig: 4-bit parallel adder (ref. 2)

D. N-Bit Parallel Subtractor

Subtraction is carried out by taking the 1's or 2's complement of the number to be subtracted.

For example, we can perform the subtraction of (A & B) by adding either 1's or 2's complement of B to A.

So, using a binary adder to perform the binary subtraction.

4 Bit Parallel Subtractor

The number to be subtracted (B) is first sent to inverters to obtain its 1's complement.

The 4-bit adder adds A and 2's complement of B for subtraction.

S3 S2 S1 S0 is the result of binary subtraction (A-B).

The carry output Cout represents the polarity of the result.

If A > B then Cout = 0 and if A<B then Cout = 1, the result is in the 2's complement form.

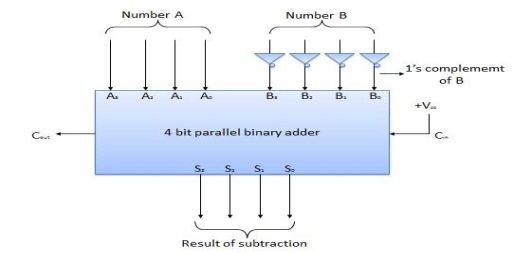
Block Diagram of Four bit Substrator

Fig: 4-bit parallel subtractor (ref. 2)

E. Half Subtractors

It is a combination circuit with two inputs and two outputs.

The difference between the two binary bits is obtained at the output and an output (Borrow) indicates if a 1 has been borrowed.

Here A is called as Minuend bit and B is called as Subtrahend bit.

Truth Table

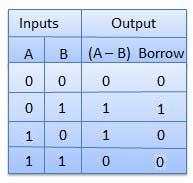
Half Substractor Truth Table

Circuit Diagram

Half Substractor Circuit Diagram

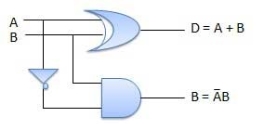
Fig: Half subtractor (ref. 2)

F. Full Subtractors

It is a combinational circuit which has three inputs A, B, C and two output D and C'.

A is the 'minuend', B is 'subtrahend', C is the 'borrow' which is produced by the previous stage, difference output D and C' is the borrow output.

Truth Table

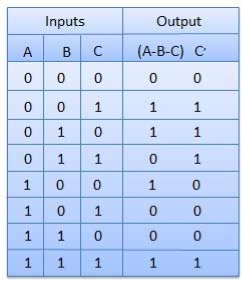
Full Substractor Truth Table

Circuit Diagram

Full Substractor Circuit Diagram

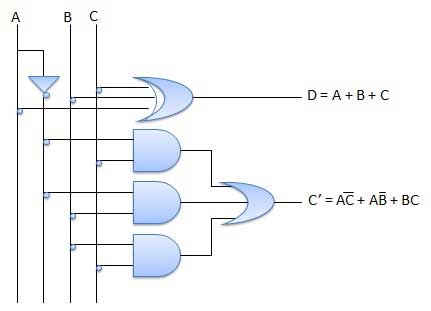
Fig: Full subtractor (ref. 2)

Carry Look-Ahead Adder

In this, for each adder block, the two bits that are to be added are available instantly.

However, each of them waits for the carry to arrive from the previous one.

So, it is impossible to generate the sum and carry of any block until the input carry is known.

The block waits for the previous block to produce its carry. So, there will be a considerable time delay which is known as carry propagation delay.

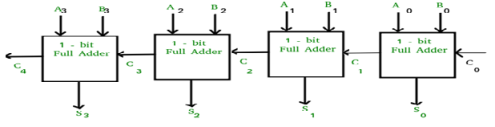
Fig: Look ahead Carry adder (ref. 2)

Here, the sum is produced by the corresponding full adder as soon as the input signals are applied to it. The carry must propagate to all the stages so that output and carry settle their final steady-state value.

The propagation time is equal to the propagation delay of each adder block, multiplied by the number of adder blocks in the circuit.

It reduces the propagation delay by introducing more complex hardware.

The ripple carry design is suitably transformed in such a way that the carry logic over fixed groups of bits is reduced to two-level logic.

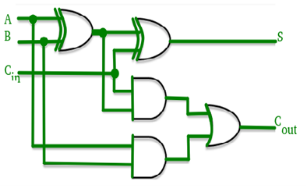
Fig: Look ahead Carry adder (ref. 2)

Advantages and Disadvantages of Carry Look-Ahead Adder:

Advantages –

The propagation delay is reduced.

It provides the fastest addition logic.

Disadvantages –

The circuit gets complicated as number of variables increase.

It is costlier as it requires more hardware.

Multiplier:

Multiplication of binary numbers is usually implemented in microprocessors and microcomputers by using repeated addition and shift operations. Since the binary adders are designed to add only two binary numbers at a time, instead of adding all the partial products at the end, they are added two at a time and their sum is accumulated in a register called the accumulator register. Also, when the multiplier bit is ‘0’, that very partial product is ignored, as an all ‘0’ line does not affect the final result. The basic hardware arrangement of such a binary multiplier would comprise shift registers for the multiplicand and multiplier bits, an accumulator register for storing partial products, a binary parallel adder and a clock pulse generator to time various operations.

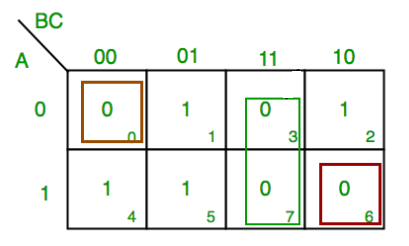
Fig: Binary Multiplier

Binary multipliers are also available in IC form. Some of the popular type numbers in the TTL family include 74261 which is a 2 × 4bit multiplier (a four-bit multiplicand designated asB0, B1, B2, B3 and B4, and a two-bit multiplier designated as M0, M1 and M2. The MSBs B4 and M2 are used to represent signs. 74284 and 74285 are 4 × 4bit multipliers. They can be used together to perform high-speed multiplication of two four-bit numbers. Figure shows the arrangement. The result of multiplication is often required to be stored in a register. The size of this register (accumulator) depends upon the number of bits in the result, which at the most can be equal to the sum of the number of bits in the multiplier and multiplicand. Some multipliers ICs have an in-built register.

Key takeaway

Half adder has two inputs and two outputs and full adder overcomes the problem faced in half adder. The full adder has three inputs including the carry bit.

2.9 An Equality Detector and comparator

It is a combinational circuit which compares two binary numbers to find whether one number is equal to, less than or greater than the other number.

A circuit is designed which has two inputs A and B and have three outputs, A > B condition, A = B condition and A < B condition.

Fig: N-bit comparator (ref.2)

1-Bit Magnitude Comparator –

It is used to compare two bits.

It consists of two single bit inputs and three outputs which compares the two binary numbers.

The truth table is given below:

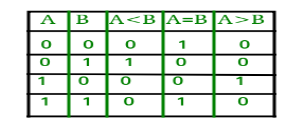
From the above truth table logical expressions for each output can be expressed as follows:

A>B: AB'

A<B: A'B

A=B: A'B' + AB

From the above expressions we can derive the following formula:

By using the above expressions, we can implement a logic circuit:

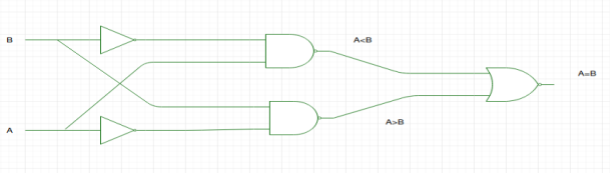
Fig: 1-bit comparator (ref.2)

2-Bit Magnitude Comparator

It is used to compare two binary numbers (two bits each).

It consists of four inputs A and B which are 2 bit each and three outputs.

The truth table is given below:

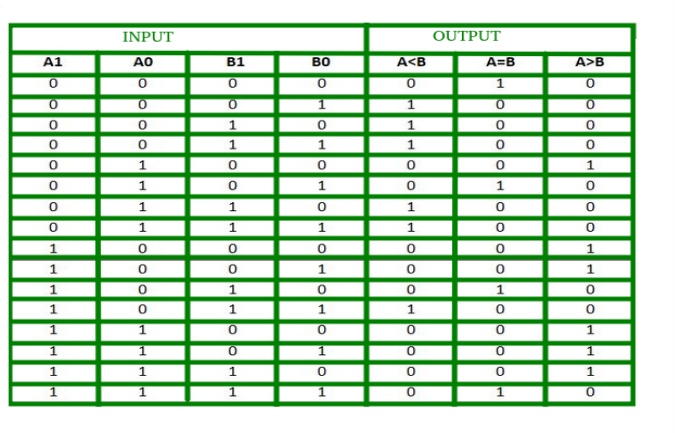
K-map for each output is as follows:

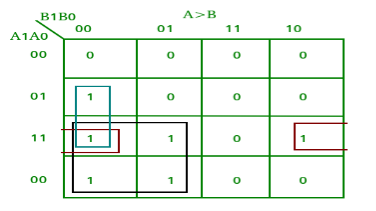
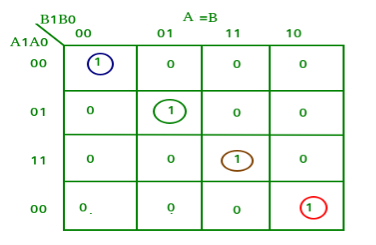
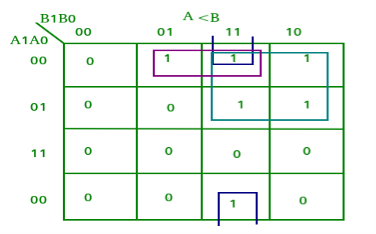
From the above K-maps output can be expressed as follows:

A>B: A1B1’ + A0B1’B0’ + A1A0B0’

A=B: A1’A0’B1’B0’ + A1’A0B1’B0 + A1A0B1B0 + A1A0’B1B0’

: A1’B1’ (A0’B0’ + A0B0) + A1B1 (A0B0 + A0’B0’)

: (A0B0 + A0’B0’) (A1B1 + A1’B1’)

: (A0 Ex-Nor B0) (A1 Ex-Nor B1)

A<B: A1’B1 + A0’B1B0 + A1’A0’B0

A logic circuit for this comparator as given below:

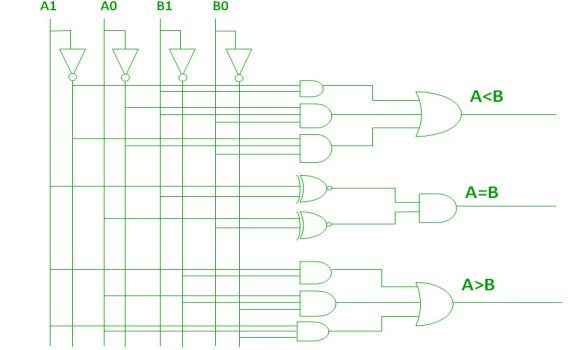
Fig: 2-bit comparator (ref.2)

4-Bit Magnitude Comparator

It is used to compare two binary numbers each of four bits.

It consists of 8 inputs each for two four-bit numbers and three outputs to generate less than, equal to and greater than between these two binary numbers.

Here, the condition of A>B is possible when:

If A3 = 1 and B3 = 0

If A3 = B3 and A2 = 1 and B2 = 0

If A3 = B3, A2 = B2 and A1 = 1 and B1 = 0

If A3 = B3, A2 = B2, A1 = B1 and A0 = 1 and B0 = 0

Similarly, the condition for A<B is possible when:

If A3 = 0 and B3 = 1

If A3 = B3 and A2 = 0 and B2 = 1

If A3 = B3, A2 = B2 and A1 = 0 and B1 = 1

If A3 = B3, A2 = B2, A1 = B1 and A0 = 0 and B0 = 1

The condition of A=B is possible when all the individual bits of one number is exactly same as another number.

The logical expressions for each output are expressed as:

AA, 831331 r: (A3 Ex-Nor 33) A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132) A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31) A01301 ,13: A3’03 a (A3 Ex-Nor 33) A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132) Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131) A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)

Implementation of a logic circuit for this comparator is given below:

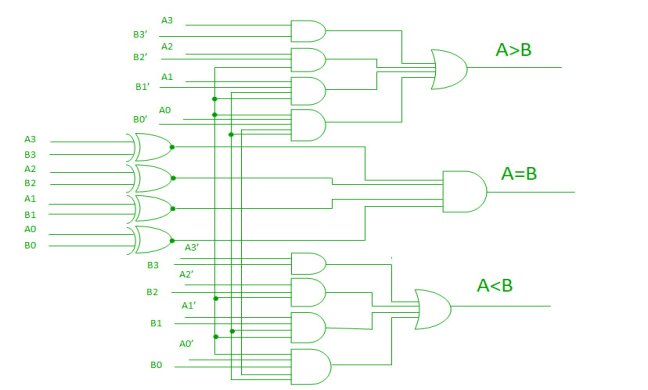
Fig: 4-bit comparator (ref.2)

Cascading Comparator –

It performs comparison operation with more than four bits by cascading two or more 4-bit comparators.

When two comparators are to be cascaded, the outputs of the lower-order comparator is connected to corresponding input of the higher-order comparator.

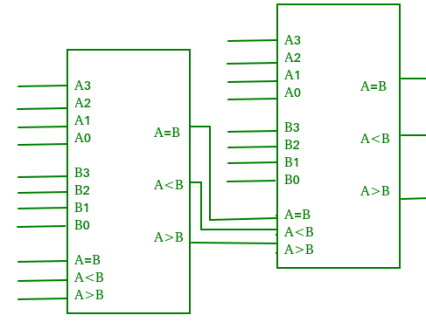
Fig: cascading comparator (ref.2)

Applications of Comparators –

They are used in central processing units (CPUs) and microcontrollers (MCUs).

They are used in control applications where the binary numbers represent physical variables such as temperature, position, etc. and are compared with a reference value.

They are also used as process controllers and Servo motor controllers.

They are used in password verification and biometric applications too.

Key takeaway

It is a combinational circuit which compares two binary numbers to find whether one number is equal to, less than or greater than the other number.

2.10 Line Decoder

It works as an inverse of an encoder.

It is a combinational circuit which converts n input lines into 2n output lines.

Taking an example of 3-to-8-line decoder.

Truth Table –

X	Y	Z	D0	D1	D2	D3	D4	D5	D6	D7
0	0	0	1	0	0	0	0	0	0	0
0	0	1	0	1	0	0	0	0	0	0
0	1	0	0	0	1	0	0	0	0	0
0	1	1	0	0	0	1	0	0	0	0
1	0	0	0	0	0	0	1	0	0	0
1	0	1	0	0	0	0	0	1	0	0
1	1	0	0	0	0	0	0	0	1	0
1	1	1	0	0	0	0	0	0	0	1

Implementation

D0 is high when X = 0, Y = 0 and Z = 0. Hence,

D0 = X’ Y’ Z’

Similarly,

D1 = X’ Y’ Z

D2 = X’ Y Z’

D3 = X’ Y Z

D4 = X Y’ Z’

D5 = X Y’ Z

D6 = X Y Z’

D7 = X Y Z

Hence,

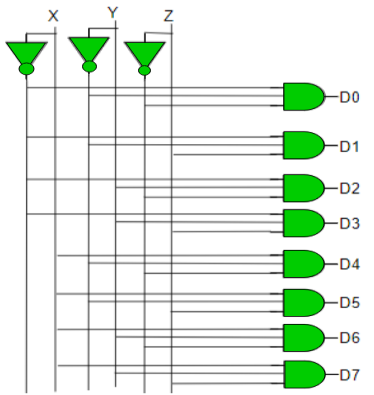
Fig: Decoder (ref.2)

Key takeaway

The decoder and demux have same internal circuit. The decoder with enable input can function as a demultiplexer. A 2x4 line decoder can act as a 1:4 demux and vice versa. Decoder contains AND gates or NAND gates.

2.11 Encoders

Binary code of N digits is used to store 2N distinct elements of coded information.

This is the reason why encoders and decoders are used.

Encoders convert 2N lines of input into a code of N bits and Decoders decode those N bits into 2N lines.

Encoders –

It is a combinational circuit that converts binary information in the form of a 2N input lines into N output lines, which represent N bit code for the input.

For simple encoders, only one input line is active at a time.

For example: Octal to Binary encoder takes 8 input lines and generates 3 output lines.

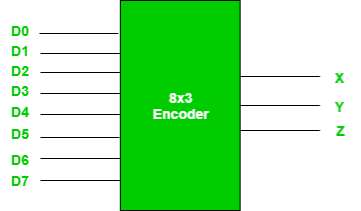
Fig: 8X3 Encoder (ref. 2)

Truth Table –

D7	D6	D5	D4	D3	D2	D1	D0	X	Y	Z
0	0	0	0	0	0	0	1	0	0	0
0	0	0	0	0	0	1	0	0	0	1
0	0	0	0	0	1	0	0	0	1	0
0	0	0	0	1	0	0	0	0	1	1
0	0	0	1	0	0	0	0	1	0	0
0	0	1	0	0	0	0	0	1	0	1
0	1	0	0	0	0	0	0	1	1	0
1	0	0	0	0	0	0	0	1	1	1

From the above truth table, it is seen that the output is 000 when D0 is active; 001 when D1 is active; 010 when D2 is active and so on.

Implementation –

From the above truth table, the output Z is active when the input octal digit is 1, 3, 5 or 7.

Y is active when input octal digit is 2, 3, 6 or 7 and X is active when input octal digits 4, 5, 6 or 7.

Hence, the Boolean functions would be:

X = D4 + D5 + D6 + D7

Y = D2 +D3 + D6 + D7

Z = D1 + D3 + D5 + D7

Hence, the encoder is realised with OR gates as follows:

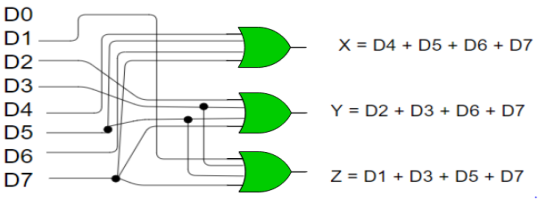
Fig: 8:3 encoder (ref.2)

Limitation of the encoder is that only one input is active at a time.

If more than one input is active, then the output of encoder is undefined.

For example, if D6 and D3 are both active, then, our output would be 111 which is the output for D7.

Problem arises when all inputs are 0.

The encoder gives output 000 which actually is the output for D0. To avoid this, an extra bit is added to the output which is called the valid bit whose value is 0 when all inputs are 0 or 1.

Priority Encoder: –

It is an encoder whose inputs are given priorities.

When more than one input becomes active at the same time then the input with higher priority takes precedence w.r.to the output which is generated.

Considering a 4:2 priority encoder.

From the truth table given below we see that when all inputs are 0, V bit is zero and outputs are not used.

The x in the table shows the don’t care condition, i.e. it can be 0 or 1.

Here, D3 has highest priority, therefore, when D3 is high, output has to be 11.

D0 has the lowest priority, hence the output would be 00 only when D0 is high and all the other input lines are low.

Truth Table –

D3	D2	D1	D0	X	Y	V
0	0	0	0	x	x	0
0	0	0	1	0	0	1
0	0	1	x	0	1	1
0	1	X	x	1	0	1
1	x	X	x	1	1	1

Implementation –
The condition for valid bit to be 1 is when at least one of the inputs should be high. Hence,

V = D0 + D1 + D2 + D3

For X:

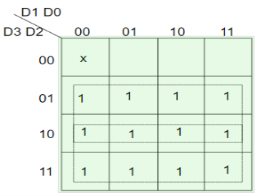
=>X=D2+D3

For Y:

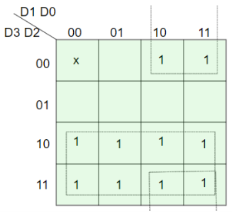
=> Y = D1 D2’ + D3

Hence, the priority 4-to-2 encoder can be realized as follows:

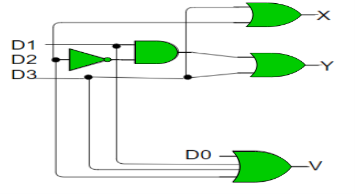
Fig: Priority encoder (ref.2)

Key takeaway

An Encoder is a combinational circuit that performs the reverse operation of Decoder. It has maximum of 2n input lines and ‘n’ output lines. It will produce a binary code equivalent to the input, which is active High.

2.12 Multiplexers and De-multiplexers

It is a special type of combinational circuit.

It has n-data inputs, one output and m inputs select lines with 2m = n.

It selects one of the n data inputs and routes it to the output.

The selection of one of the inputs is done by the select lines.

Depending on the code applied at the inputs, one of the n data sources is selected and transmitted to the single output Y.

E is the enable input which is useful for cascading purpose.

It is an active low terminal hence performs the required operation when it is low.

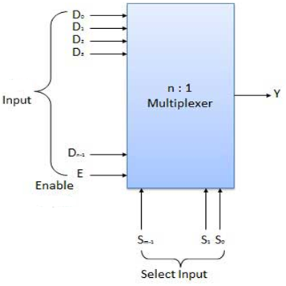
Fig: Block diagram of multiplexer (ref. 2)

Multiplexers come in multiple variations

2: 1 multiplexer

4: 1 multiplexer

16: 1 multiplexer

32: 1 multiplexer

Block Diagram of 2:1 MUX

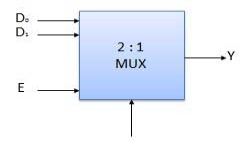
2:1 Multiplexer Block Diagram

Truth Table of 2:1 MUX

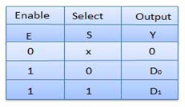
Where x is don’t care.

Demultiplexers

It performs the inverse operation of a multiplexer as it receives one input and distributes it across its outputs.

It has only one input and n outputs with m select input.

At a time only one output line is selected by the select lines and that input is transmitted through the output line.

It is equivalent to a single pole multiple way switch.

Various Demultiplexers are used as:

1: 2 demultiplexer

1: 4 demultiplexer

1: 16 demultiplexer

1: 32 demultiplexer

Block diagram

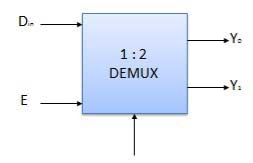
Block Diagram of 1:2 Demultiplexer

Truth Table

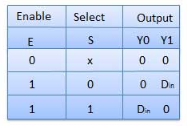
Where x is don’t care.

References:

Digital Design, 3rd Edition, Moris M. Mano, Pearson Education.

Fundamentals of digital circuits, 8th edition, A. Anand Kumar, PHI

Digital Fundamentals, 5th Edition, T.L. Floyd and R.P. Jain, Pearson Education, New Delhi.

Digital Electronics, G. K. Kharate, Oxford University Press.

Digital Systems – Principles and Applications, 10th Edition, Ronald J. Tocci, Neal S. Widemer and Gregory L. Moss, Pearson Education.

A First Course in Digital System Design: An Integrated Approach, India Edition, John P. Uyemura, PWS Publishing Company, a division of Thomson Learning Inc.

Digital Systems – Principles and Applications, 10th Edition, Ronald J. Tocci, Neal S. Widemer and Gregory L. Moss, Pearson Education.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined