Unit - 3
Synchronous Sequential logic Design

Fig. 1 Combinational circuit
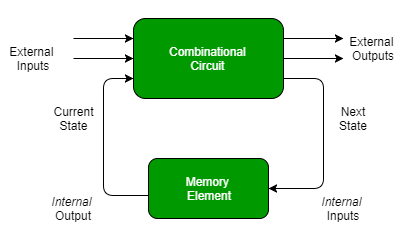
Fig. 2 Sequential circuit
There are two types of input to the combinational logic in fig 2:
Secondary inputs are state variables that are produced by the storage elements whereas secondary outputs are excitations for those storage elements.
Types of Sequential Circuits –
There are two types of sequential circuit:
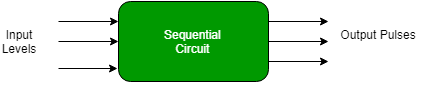
Fig. 3 Asynchronous Sequential circuit
But they are more difficult to design and their output is also uncertain.
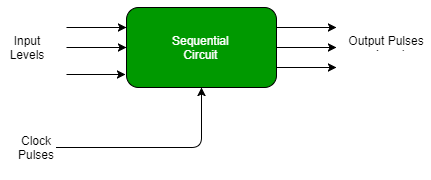
Fig. 4 Synchronous Sequential circuit
Key takeaway
Latches are basic storage elements that operate with signal levels (rather than signal transitions). Latches controlled by a clock transition are flip-flops. Latches are edge-sensitive devices. Latches are useful for the design of the asynchronous sequential circuit.
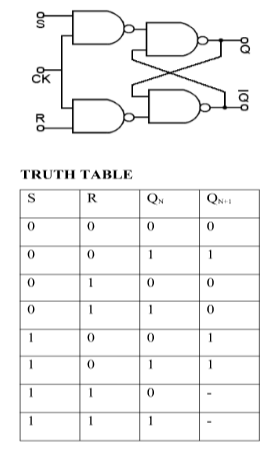
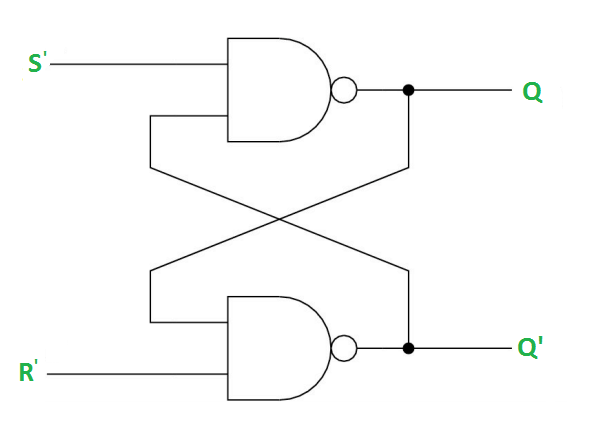
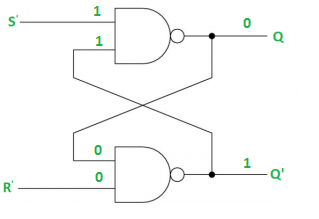
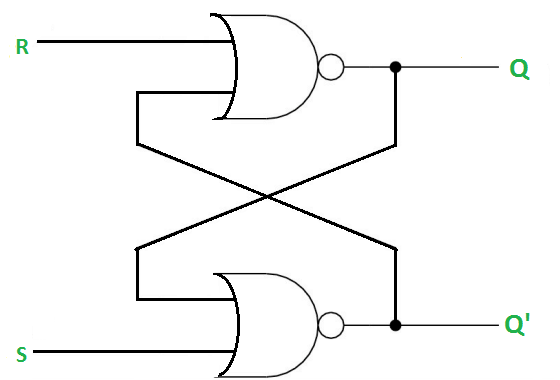
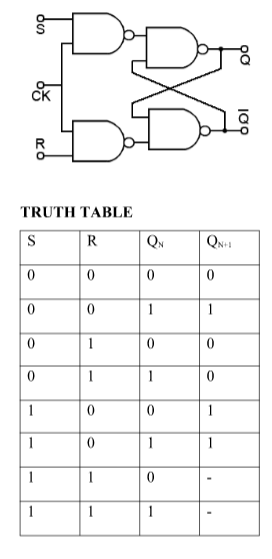
SR (Set-Reset) Latch –
SR Latch is a circuit which has:
(i) 2 cross-coupled NOR gate or NAND gate.
(ii) 2 input S for SET and R for RESET.
(iii) 2 output Q and Q’.
Q | Q’ | STATE |
1 | 0 | Set |
0 | 1 | Reset |
Under normal conditions, both the input remains 0.
RS Latch with NAND gates:
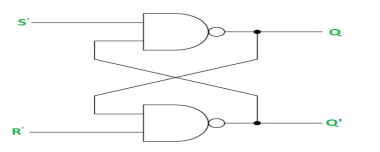
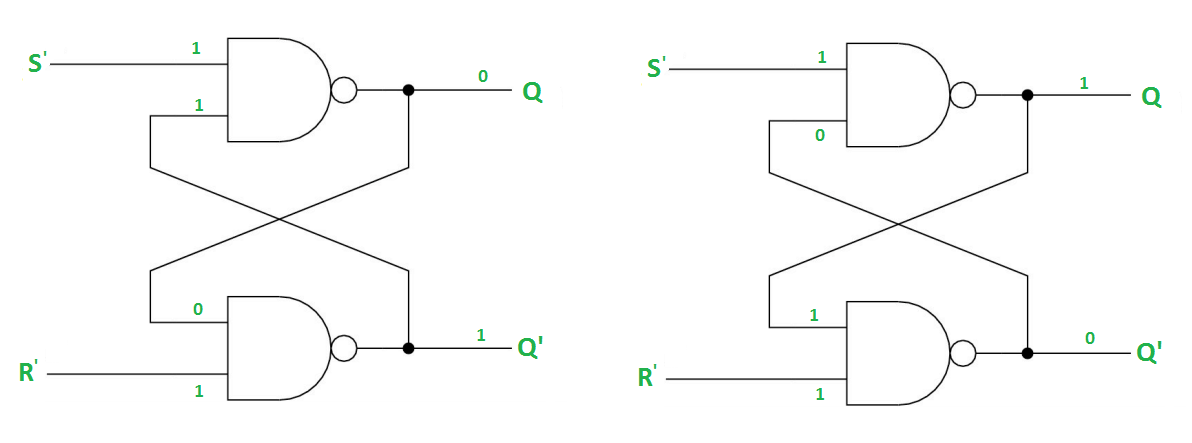
Case-1: When S’=R’=1 or S=R=0 then
If Q = 1, Q = R’ = 1.
If Q = 0, Q = 0 and R’ = 1 respectively.
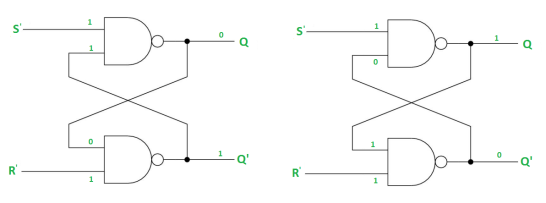
Case-2: S’=0, R’=1 (S=1, R=0)
As S’=0, Q = 1(SET state).
In 2nd NAND gate, as Q = R’ = 1, Q’=0.
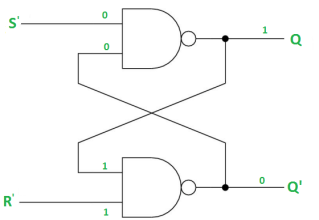
Case-3: S’= 1, R’= 0 (S=0, R=1)
As R’=0, Q’ = 1.
In 1st NAND gate, as Q =S’ = 1, Q=0 (RESET state).
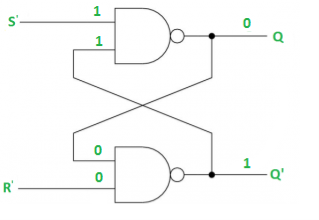
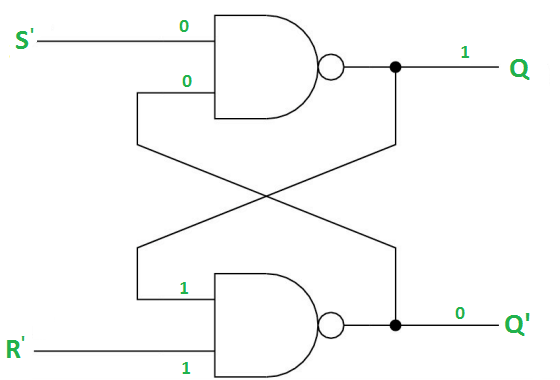
Case-4: S’= R’= 0 (S=R=1)
When S=R=1, both Q = Q’ = 1 which is not allowed.
So, this input condition is prohibited.
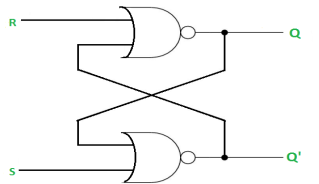
The SR Latch using NOR gate is:
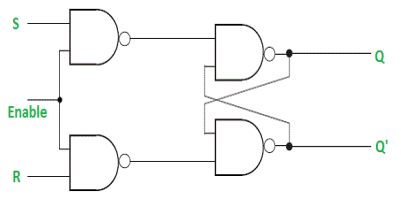
Gated SR Latch –
It is a latch which enable input that works when enable = 1 and retain the previous state when enable = 0.
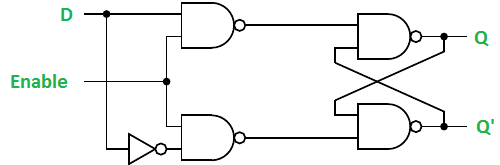
Gated D Latch –
It is similar to SR latch with little modifications. Here, the inputs are complements of one another. The design of D latch with Enable signal is given below:
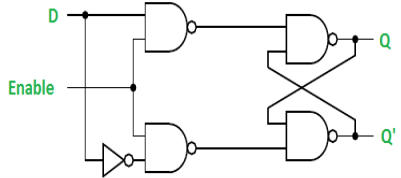
The truth table is shown below:
ENABLE | D | Q(N) | Q(N+1) | STATE |
1 | 0 | x | 0 | RESET |
1 | 1 | x | 1 | SET |
0 | x | x | Q(n) | No Change |
As the output is same as input, it is also known as Transparent Latch.
The characteristic equation for D latch with enables input is given as:
Q(n+1) = EN. D + EN’. Q(n)
Key takeaway
Latches are basic storage elements that operate with signal levels (rather than signal transitions). Latches controlled by a clock transition are flip-flops. Latches are edge-sensitive devices.
Logic diagrams and truth tables of the various types of flip-flops are as follows:
S-R Flip Flop:
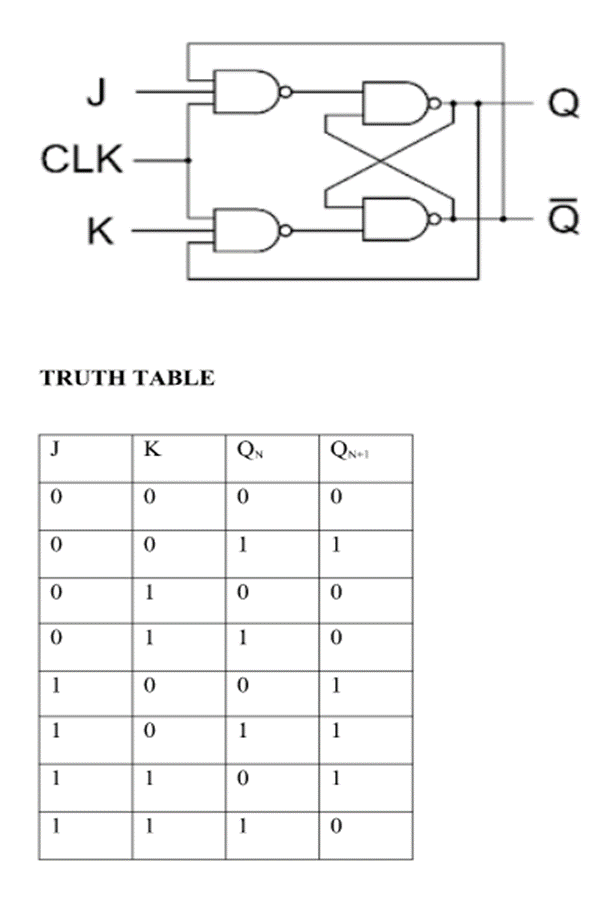
J-K Flip Flop:
D Flip Flop:
T Flip Flop:
Race Around Condition in JK Flip-flop –
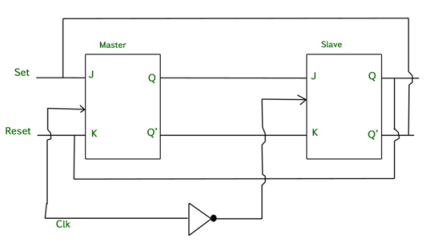
Fig. 5 Master Slave Flip flop
Working of a master slave flip flop –
Timing Diagram of a Master flip flop –
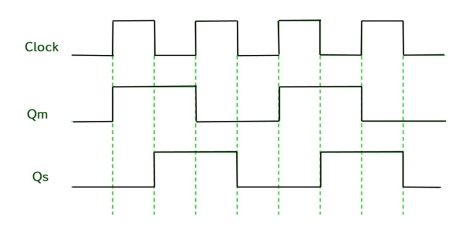
Key takeaway
The state table representation of a sequential circuit consists of three sections labeled present state, next state and output. The present state designates the state of flip-flops before the occurrence of a clock pulse. The next state shows the states of flip-flops after the clock pulse, and the output section lists the value of the output variables during the present state.
State Diagram
In addition to graphical symbols, tables or equations, flip-flops can also be represented graphically by a state diagram. In this diagram, a state is represented by a circle, and the transition between states is indicated by directed lines (or arcs) connecting the circles.
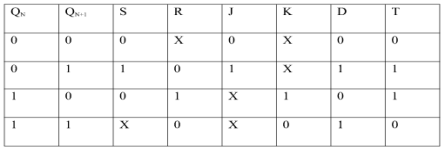
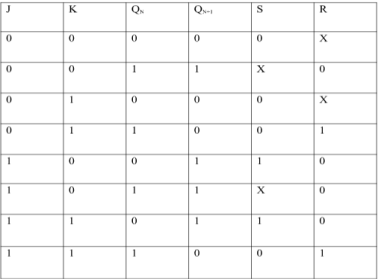
EXCITATION TABLE:
Excitation Functions:
ii) Convert SR to D Flip-Flop:
Excitation Functions:
S = D
R = D ‘
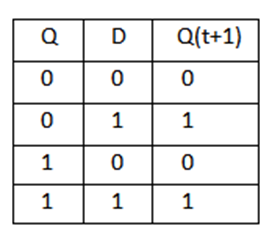
Key takeaway
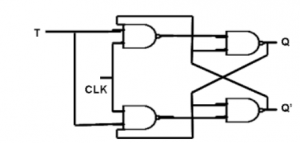
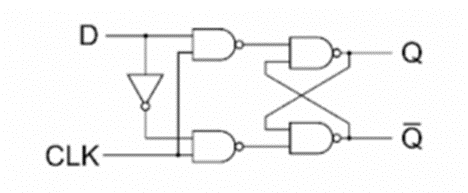
Positive Edge Triggered D Flip-flop
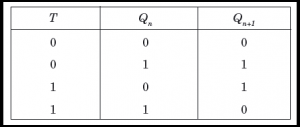
Fig: Circuit Diagram
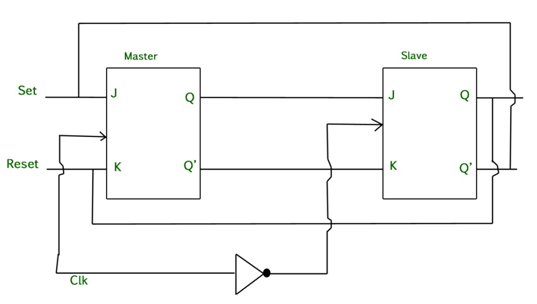
Fig 7 Symbol

Fig 8 State Table
- When R = 0, the output is set to 0 (independent of D and Clock).
- The clock at Clock is shown with an upward arrow to indicate that the flip-flop triggers on the positive edge of the clock.
- The value in D is transferred to Q with every positive-edge clock signal provided that R = 1.
Analysis with D Flip-Flops
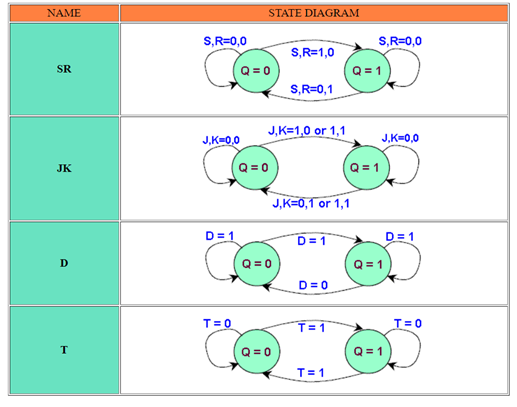
Fig 9 Circuit Diagram
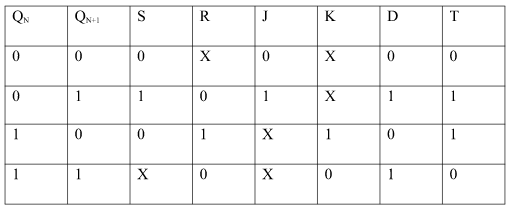
Fig 10 State Table
Analysis with JK Flip-Flops
- JA = B; KA = Bx'
- JB = x'; KB = A'x + Ax' = A ⊕ x
- When J = 1 and K = 0 the next state is 1
- When J = 0 and K = 1 the next state is 0
- When J = 0 and K = 0 there is no change of state and the next-state value is the same as that of the present state.
- When J = K = 1, the next-state bit is the complement of the present-state bit.
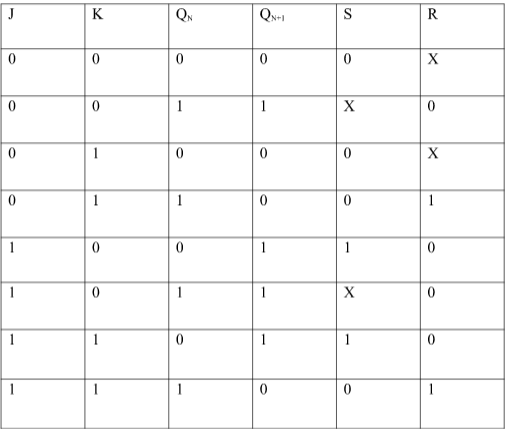
Fig 11 Circuit Diagram
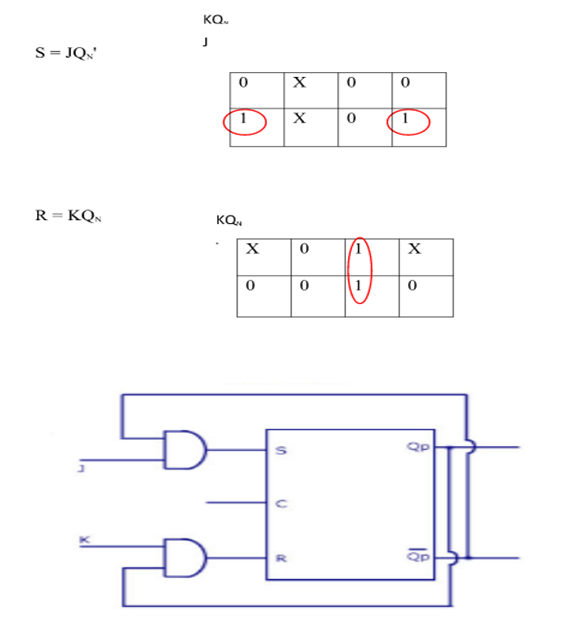
Fig 12 State Table
- A (t + 1) = JA' + K'A
- B (t + 1) = JB' + K'B
A (t + 1) = BA' + (Bx')'A = A'B + AB' + Ax
- B (t + 1) = x'B' + (A ⊕ x)'B = B'x' + ABx + A'Bx'
Analysis with T Flip-Flops
- Q(t+1) = T ⊕ Q = T'Q + TQ'
- TA = Bx
- TB = x
- y = AB
- A (t + 1) = (Bx)' A + (Bx)A' = AB' + Ax' + A'Bx
- B (t + 1) = x ⊕ B
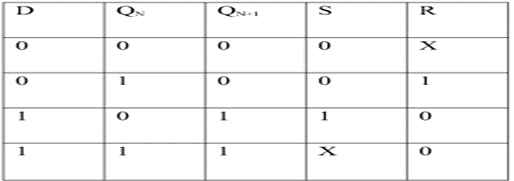
Fig 13 Circuit Diagram
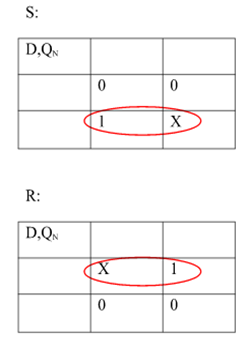
Fig 14 State Table
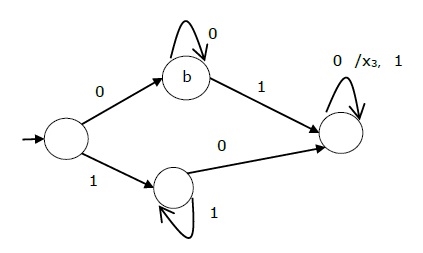
Mealy Machine
A Mealy Machine is an FSM whose output depends on the present state as well as the present input.
It can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −
The state table of a Mealy Machine is shown below −
Present state | Next state | |||
input = 0 | input = 1 | |||
State | Output | State | Output | |
→ a | b | x1 | c | x1 |
b | b | x2 | d | x3 |
c | d | x3 | c | x1 |
d | d | x3 | d | x2 |
The state diagram of the above Mealy Machine is −
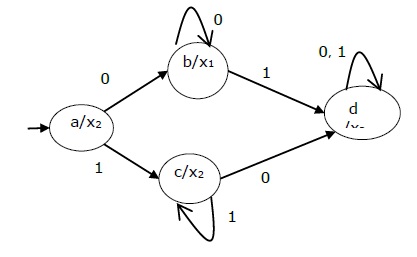
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.
A Moore machine can be described by a 6 tuple (Q, ∑, O, δ, X, q0) where −
The state table of a Moore Machine is shown below −
Present state | Next State | Output | |
Input = 0 | Input = 1 | ||
→ a | b | c | x2 |
b | b | d | x1 |
c | c | d | x2 |
d | d | d | x3 |
The state diagram of the above Moore Machine is −
Mealy Machine vs. Moore Machine
The following table highlights the points that differentiate a Mealy Machine from a Moore Machine.
Mealy Machine | Moore Machine |
Output depends both upon the present state and the present input | Output depends only upon the present state. |
Generally, it has fewer states than Moore Machine. | Generally, it has more states than Mealy Machine. |
The value of the output function is a function of the transitions and the changes, when the input logic on the present state is done. | The value of the output function is a function of the current state and the changes at the clock edges, whenever state changes occur. |
Mealy machines react faster to inputs. They generally react in the same clock cycle. | In Moore machines, more logic is required to decode the outputs resulting in more circuit delays. They generally react one clock cycle later. |
References: