Unit - 1
Classification of Engineering Materials
Engineering materials refers to the group of materials that are used in the construction of manmade structures and components. The primary function of an engineering material is to withstand applied loading without breaking and without exhibiting excessive deflection. The major classifications of engineering materials include metals, polymers, ceramics, and composites. The important characteristics of the materials within each of these classes are discussed on this page, and tables of material properties are also provided.
Metals
Metals are the most commonly used class of engineering material. Metal alloys are especially common, and they are formed by combining a metal with one or more other metallic and/or non-metallic materials. The combination usually occurs through a process of melting, mixing, and cooling. The goal of alloying is to improve the properties of the base material in some desirable way.
Metal alloy compositions are described in terms of the percentages of the various elements in the alloy, where the percentages are measured by weight.
Ferrous Alloys
Ferrous alloys have iron as the base element. These alloys and include steels and cast irons. Ferrous alloys are the most common metal alloys in use due to the abundance of iron, ease of production, and high versatility of the material. The biggest disadvantage of many ferrous alloys is low corrosion resistance.
Carbon is an important alloying element in all ferrous alloys. In general, higher levels of carbon increase strength and hardness, and decrease ductility and weldability.
Carbon SteelCarbon steels are basically just mixtures of iron and carbon. They may contain small amounts of other elements, but carbon is the primary alloying ingredient. The effect of adding carbon is an increase in strength and hardness.
Most carbon steels are plain carbon steels, of which there are several types.
Low-Alloy SteelLow-alloy steels, also commonly called alloy steels, contain less than about 8% total alloying ingredients. Low-alloy steels are typically stronger than carbon steels and have better corrosion resistance.
Some low-alloy steels are designated as high-strength low-alloy (HSLA) steels. What sets HSLA steels apart from other low-alloy steels is that they are designed to achieve specific mechanical properties rather than to meet a specific chemical composition
Tool SteelTool steels are primarily used to make tooling for use in manufacturing, for example cutting tools, drill bits, punches, dies, and chisels. Alloying elements are typically chosen to optimize hardness, wear resistance, and toughness.
Stainless SteelStainless steels have good corrosion resistance, mostly due to the addition of chromium as an alloying ingredient. Stainless steels have a chromium composition of at least 11%. Passivation occurs with chromium content at or above 12%, in which case a protective inert film of chromic oxide forms over the material and prevents oxidation. The corrosion resistance of stainless steel is a result of this passivation.
Cast IronCast iron is a ferrous alloy containing high levels of carbon, generally greater than 2%. The carbon present in the cast iron can take the form of graphite or carbide. Cast irons have a low melting temperature which makes them well suited to casting.
Gray Cast IronGray cast iron is the most common type. The carbon is in the form of graphite flakes. Gray cast iron is a brittle material, and its compressive strength is much higher than its tensile strength. The fracture surface of gray cast iron has a gray color, which is how it got its name.
Ductile Cast Iron (Nodular Cast Iron)The addition of magnesium to gray cast iron improves the ductility of the material. The resulting material is called nodular cast iron because the magnesium causes the graphite flakes to form into spherical nodules. It is also called ductile cast iron. Nodular cast iron has good strength, ductility, and machinability. Common uses include crankshafts, gears, pump bodies, valves, and machine parts.
White Cast IronWhite cast iron has carbon in the form of carbide, which makes the material hard, brittle, and difficult to machine. White cast iron is primarily used for wear-resisting components as well as for the production of malleable cast iron.
Malleable Cast IronMalleable cast iron is produced by heat treating white cast iron. The heat treatment improves the ductility of the material while maintaining its high strength.
Aluminum Alloys
Pure aluminum is soft and weak, but it can be alloyed to increase strength. Pure aluminum has good corrosion resistance due to an oxide coating that forms over the material and prevents oxidation. Alloying the aluminum tends to reduce its corrosion resistance.
Aluminum is a widely used material, particularly in the aerospace industry, due to its light weight and corrosion resistance. Despite the fact that aluminum alloys are generally not as strong as steels, they nevertheless have a good strength-to-weight ratio.
Nickel Alloys
Nickel alloys have high temperature and corrosion resistance. Common alloying ingredients include copper, chromium, and iron. Common nickel alloys include Monel, K-Monel, Inconel, and Hastelloy
Copper Alloys
Copper alloys are generally characterized as being electrically conductive, having good corrosion resistance, and being relatively easy to form and cast. While they are a useful engineering material, copper alloys are also very attractive and are commonly used in decorative applications.
Copper alloys primarily consist of brasses and bronzes. Zinc is the major alloying ingredient in brass. Tin is a major alloying element in most bronzes. Bronzes may also contain aluminum, nickel, zinc, silicon, and other elements. The bronzes are typically stronger than the brasses while still maintaining good corrosion resistance.
Titanium Alloys
Titanium alloys are light, strong, and have high corrosion resistance. Their density is much lower than steel, and their strength-to-weight ratio is excellent. For this reason, titanium alloys are used fairly commonly, especially in the aerospace industry. One primary downside of titanium alloys is the high cost.
There are three categories of titanium alloys: alpha alloys, beta alloys, and alpha-beta alloys. Alpha alloys do not respond to heat treatment and are instead strengthened through solid-solution strengthening processes. The beta and alpha-beta alloys can be strengthened by heat treatment, primarily through precipitation hardening.
Polymers
Polymers are materials that consist of molecules formed by long chains of repeating units. They may be natural or synthetic. Many useful engineering materials are polymers, such as plastics, rubbers, fibers, adhesives, and coatings. Polymers are classified as thermoplastic polymers, thermosetting polymers (thermosets), and elastomers.
Thermoplastic Polymers
The classification of thermoplastics and thermosets is based on their response to heat. If heat is applied to a thermoplastic, it will soften and melt. Once it is cooled, it will return to solid form. Thermoplastics do not experience any chemical change through repeated heating and cooling (unless the temperature is high enough to break the molecular bonds). They are therefore very well suited to injection molding.
Thermosetting Polymers
Thermosets are typically heated during initial processing, after which they become permanently hard. Thermosets will not melt upon reheating. If the applied heat becomes extreme however, the thermoset will degrade due to breaking of the molecular bonds. Thermosets typically have greater hardness and strength than thermoplastics. They also typically have better dimensional stability than thermoplastics, meaning that they are better at maintaining their original dimensions when subjected to temperature and moisture changes.
Elastomers
Elastomers are highly elastic polymers with mechanical properties similar to rubber. Elastomers are commonly used for seals, adhesives, hoses, belts, and other flexible parts. The strength and stiffness of rubber can be increased through a process called vulcanization, which involves adding sulfur and subjecting the material to high temperature and pressure. This process causes cross-links to form between the polymer chains.
Ceramics
Ceramics are solid compounds that may consist of metallic or nonmetallic elements. The primary classifications of ceramics include glasses, cements, clay products, refractories, and abrasives.
Ceramics generally have excellent corrosion and wear resistance, high melting temperature, high stiffness, and low electrical and thermal conductivity. Ceramics are also very brittle materials.
Glass
Glasses are common materials and are seen in applications including windows, lenses, and containers. Glasses are amorphous, whereas the other ceramics are mainly crystalline. Primary advantages of glasses include transparency and ease of fabrication. The base element of most glasses is silica, and other components can be added to modify its properties. Common processes used to form glass include:
Cements
Cements are materials that, after mixing with water, form a paste that then hardens. Because of this characteristic, cements can be formed into useful shapes while in paste form before they harden into rigid structures. Plaster of Paris is one common cement. The most common cement is called Portland cement, which is made by mixing clay and limestone and then firing at high temperature. Portland cement is used to form concrete, which is made by mixing it with sand, gravel, and water. It can also be mixed with sand and water to form mortar. Like other ceramics, cements are weak in tension but strong in compression. Cement is very inexpensive to produce, and it is used widely in the construction of buildings, bridges, and other large structures.
Clay Products
Clay is a very common ceramic material. It can be mixed with water, shaped, and then hardened through firing at high temperature. The two primary classifications of clay products include structural clay products and whitewares. Structural clay products see applications including bricks, tiles, and piping. Whitewares see applications including pottery and plumbing fixtures.
Refractories
Refractory ceramics can withstand high temperatures and extreme environments. They can also provide thermal insulation. Brick is the most common refractory ceramic.
Abrasives
Abrasive ceramics are hard materials that are used to cut, grind, and wear away other softer materials. Typical properties of abrasives include high hardness, wear resistance, and temperature resistance. Abrasives can either be bonded to a surface (e.g., grinding wheels and sandpaper), or can be used as loose grains (e.g., sand blasting). Common abrasives include cemented carbide, silicon carbide, tungsten carbide, aluminum oxide, and silica sand. Diamond is also an excellent abrasive, but it is expensive.
A) Mechanical properties
The mechanical properties of materials are those which affect the mechanical strength and ability of a material to be moulded in desired shape.
Some of them are as follows: -
1) Strength
2) Hardness
3) Toughness
4) Malleability
5) Hardenability
6) Brittleness
7) Ductility
8) Creep and slip
9) Resilience
10) Fatigue
(B) Optical properties
Optical property of a material is defined as its interaction with electromagnetic radiation in the visible.
Optical materials are classified on the basis of their interaction with visible-light into three categories
1) Optical properties – Metals: -
2) Optical properties: - Nonmetals: -
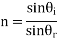
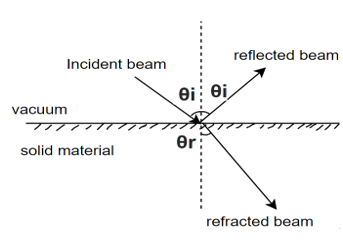
Snell's law of light reflection
Reflection: - Reflectivity is defined as fraction of light reflected at an interface
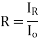
If the material is in the other material with refractive index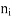 
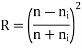
Absorption: - When a light beam is impinged on the incident beam that is not reflected by the material is either absorbed or transmitted through the material.
Optical applications: -
1) Luminescence
2) Lasers
3) Thermal emission
4) Photoconductivity
5) Optical fibers
B) Electrical properties
The electrical properties of a material are those which determine ability of a material to be suitable for a particular electrical engineering.
Some of them are as follows: -
1) Resistivity
2) Conductivity
3) Temperature coefficient of resistance
4) Permittivity
5) Thermal electricity
6) Dielectric strength
Resistivity: - Properly of a material which resists the flow of electrical current through material. It is the reciprocal of conductivity.
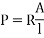
S.I unit = Ωm
Where, R = resistance of conductor in Ω
A = cross sectional area
l = length of the conductor in 'm'.
Conductivity: -
It is the property of a material which allows the flow of current. It is denoted by 
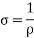
S.I unit =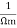 
Dielectric Strength: - Property of a material which indicates the ability of material to withstand at high voltages.
S.I. unit = KV/cm
Temperature coefficient of resistance: -
Property of a material which indicates the change in resistance of material with change in temperature.
It is denoted by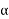 
Thermoelectricity: - It is the function formed by joining of two metals when heated, a small voltage in the range milli volt is product. This effect is called thermal electricity.
Metals are lustrous, malleable, ductile, good conductors of heat and electricity. Other properties include:
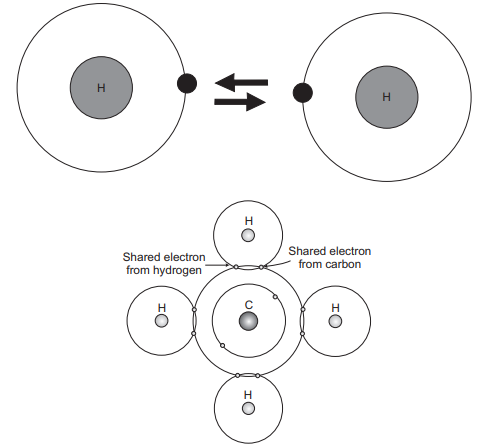
A comprehension of a large number of the physical properties of materials is predicated on information of the nuclear powers that quandary the particles together. Maybe the standards of nuclear holding are best represented by considering the connection between two confined particles as they are brought into closeness from an interminable division. Everywhere the connections are insignificant, however as the molecules approach, each repels the other. These powers are of two sorts, alluring and appalling, and the greatness of each is an element of the detachment or interatomic separation.
The orbit of an alluring power FA relies on the specific kind of holding that exists between the two molecules. The size of the alluring power shifts with the separation, as shown schematically in Figure 2.7a. At last, the external electron shells of the two atoms start to cover, and a solid shocking power FR becomes possibly the most important factor. The net compel FN between the two molecules is only the total of both alluring and terrible parts; that is
FN = FR + FA
Three unique sorts of primary or chemical bond are found in solids—ionic, covalent, and metallic. For every sort, the holding essentially includes the valence electrons; moreover, the nature of the bond relies on the electron structures of the constituent molecules. By and large, each of these three sorts of holding emerges from the inclination of the molecules to expect stable electron structures, similar to those of the inactive gasses, by totally filling the furthest electron shell. Auxiliary or physical strengths and energies are likewise found in numerous strong materials; they are weaker than the essential ones, yet regardless impact the physical properties of a few materials. The segments that take after clarify the few sorts of essential and auxiliary between nuclear or atomic bonds.
Ionic Bonds:
Ionic bonding may be the least demanding to depict and picture. It is constantly found in abundance that are made out of both metallic and non-metallic elements. Elements that are arranged at the flat limits of the occasional table. Molecules of a metallic element effortlessly surrender their valence electrons to the non-metallic atoms. In the process every one of the molecules procures steady or inactive gas setups and, furthermore, an electrical charge; that is, they get particles. Sodium chloride (NaCl) is an exemplary ionic material. A sodium molecule can accept the electron structure of neon (and a net single positive charge) by an exchange of its one valence 3s electron to a chlorine particle. After such an exchange, the chlorine particle has a net negative charge and an electron setup indistinguishable to that of argon. In sodium chloride, all the
Hence, we can summarize that this bond exists between two atoms when one of the atoms is negative (has an additional electron) and another is positive (has lost an electron). At that point there is a solid, coordinate Coulomb fascination. Essentially, ionic bonds are non-directional in nature. An illustration is NaCl. In the particle, there are more electrons around Cl, shaping Cl– and less electrons around Na, framing Na+. Ionic bonds are the most grounded bonds. In genuine solids, ionic holding typically exists alongside covalent holding
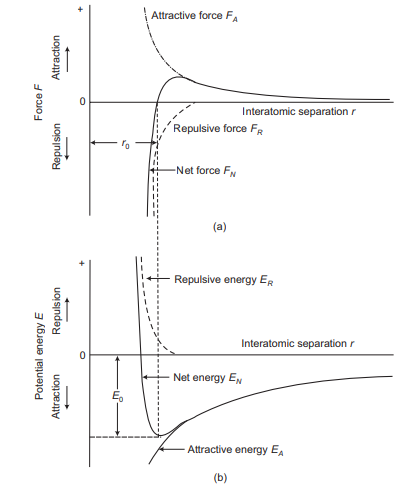
In covalent bonding, stable electron setups are expected by the sharing of electrons between neighbouring atoms. Two atoms that are covalently fortified will each contribute no less than one electron to the bond, and the mutual electrons might be considered to have a place with both particles. Covalent holding is schematically delineated in Figure 2.9 for an atom of methane (CH4). The carbon particle has four valence electrons, though each of the four hydrogen molecules has a solitary valence electron. Every hydrogen iota can obtain a helium electron arrangement (two 1s valence electrons) when the carbon molecule offers with it one electron. Carbon now has four extra shared electrons, one from every hydrogen, for an aggregate of eight valence electrons, and the electron structure of neon. The covalent bond is directional; that is, it is between particular particles and may exist just in the course between one iota and another that takes part in the electron sharing.
Hence, we can summarize covalent bonding that in this type of bonding electrons are shared between the atoms, to soak the valency. The most straightforward case is the H2 particle, where the electrons invest more energy in the middle of the cores of two iotas than outside, along these lines delivering holding. Covalent bonds are stereo particular, i.e., every bond is between a particular match of particles, which share a couple of electrons (of inverse attractive twists). Regularly, covalent bonds are exceptionally solid, and directional in nature. The hardness of precious stone is an aftereffect of the way that every carbon molecule is covalently reinforced with four neighbouring particles, and every neighbour is fortified with an equivalent number of atoms to shape an inflexible three-dimensional structure
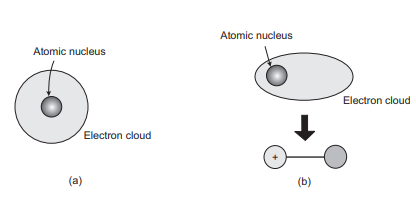
The last essential bonding sort, is found in metals and their alloys. A moderately basic model has been recommended that practically approximates the bonding plan. Metallic materials have one, two, or at most, three valence electrons. With this model, these valence electrons are not bound to a specific molecule in particular and are pretty much allowed to float all through the whole metal. They might be considered having a place with the metal overall, or framing an “ocean of electrons” or an “electron cloud.” The rest of the non-valence electrons and nuclear cores shape called ions core, have a net positive charge rise to in size to the aggregate valence electron charge per iota. Figure 2.10 is a schematic outline of metallic holding. The free electrons shield the decidedly charged particle centres from commonly horrible electrostatic strengths, which they would some way or another apply upon each other; consequently, the metallic bond is non-directional in character. Likewise, these free electrons go about as a “paste” to hold the particle cores together. Metallic bonding is found in the occasional table for Group IA and IIA elements and, truth be told, for every elemental metal. Some broad conduct of the different material sorts (i.e., metals, earthenware production, polymers) might be clarified by holding sort. For instance, metals are great channels of both power and warmth, as a result of their free electrons. By the method for difference, ionically and covalently reinforced materials are regularly electrical and warm separators, because of the nonappearance of vast quantities of free electrons.
Quick and brief mutilations of this electrical symmetry for a portion of the iotas or atoms, and the formation of little electric dipoles, as shown in Figure 2.12b. One of these dipoles can thus deliver a relocation of the electron conveyance of an adjoining particle or atom, which instigates the second one likewise to wind up a dipole that is then pitifully pulled in or attached to the main; this is one sort of van der Waals bonding. These alluring powers may exist between huge quantities of particles or atoms, which strengths are impermanent and vacillate with time
Atom arrangement in material: -
Depending upon the manner of atomic grouping, materials are classified as molecular structure, crystal structure and amorphous (irregular structure).
Molecular structure: This structure has a number of atoms that are held together by primary bond. E.g.: -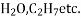 
Crystal structure: - In glass the atoms are not regular. This is called amorphous structure.
Unit cell: - A unit cell is defined as the basic structure of atoms arranged in a material. Different forms of unit cell have different length, different angles as given below:
(1) Cubic structure: - a = b = c
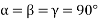
a = length of the unit cell along x axis
b = length of the unit cell along y axis
c = length of the unit cell along Z axis
(2) Tetragonal structure: - a = b ≠c: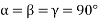
(3) Orthometric: - a ≠b ≠ c: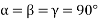 
(4) Monoclinic: - a ≠ b ≠ c: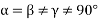
(5) Triclinic: - a ≠b ≠ c: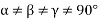 
(6) Rhombohedral: - a = b = c: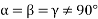
(7) Hexagonal: - a = b ≠ c: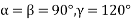
(1) Simple cubic (SC): - Atoms are arranged at the corner of the cell.
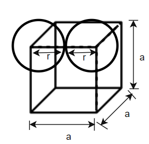
Total number of atoms = 8
Number of atoms at each corner 
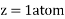
Edge length a = 2r
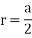
Packing efficiency: - volume of spaces occupied by the space
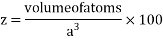
Where z = number of atoms per unit cell
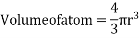
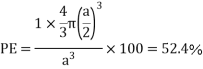
Total space occupied by spares =52.4
Empty space = 100 – 52.4 = 47.6%
2) Body centered cubic (BCC): Atoms are arranged at the corners of the cube with other atoms at the cubic center.
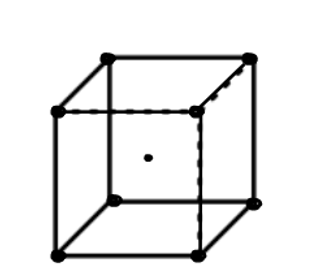
Number of atoms in corner = 8
Number of atoms in each corner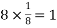 
Number of atoms in middle =1
Total atoms = z = 1 + 1 = 2
According to Pythagoras theorem
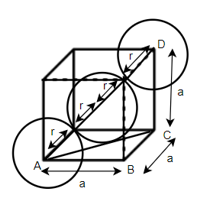
In ∆ADC
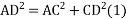
Where AD = 4r
CD = a
AC =?
So, ∆ABC
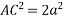
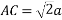
Putting the values in equation (1)
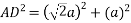
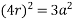
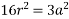
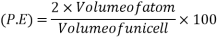
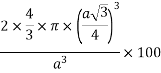
So, volume occupied by the space = 68%
Empty space =32%
Example: - Mg, Na, K, Li
(3) FCC (Face center of cubic): - Atoms are arranged at the corners of each cube for the cell.
Total number of atoms in corner = 8
Each atom in corner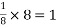 
Atoms in each face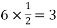 
So total atoms in cell = 1 + 3 = 4
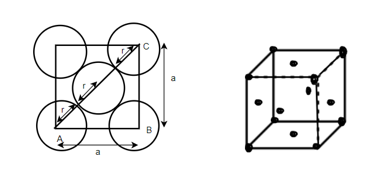
In ∆ABC
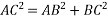
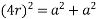
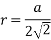
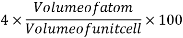
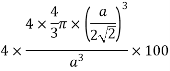
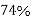
Volume occupied by the space = 7 empty space = 26
Example: - Al, Ag etc.
(4) HCP (hexagonal closed packed)
Cell on a hexagon closed packed lattice is visualized at top 4 bottoms plane of atoms forming a regular hexagon around a central atom.
There are two lattice parameters in hexagonal close-packed, a and c representing the basal 4 height parameters respectively.
Number of atoms in corners = 12
Number of atoms in each corner = 
Number of atoms in mid = 01
Number of atoms in top 4 bottom face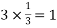 
Total atoms = 4+01+01=06
Relation between a and r: -
In hexagonal close packed structure, the atom is in contact with each other along the cube edge.
Volume of unit cell: - area of hexagon × h
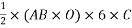
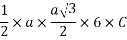
Now, 
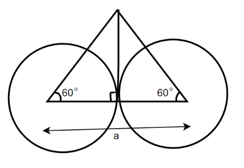
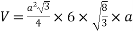
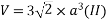
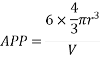
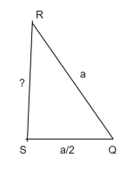
Consider three body atoms PQR
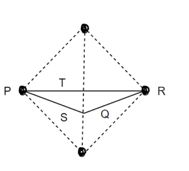
A median is drawn from r to PQ which meets at point S
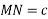
PQR is equilateral triangle.
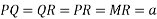
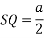
RSQ is a right-angled triangle
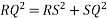
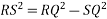
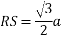
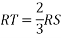
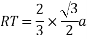
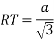
MTR is right angled triangle
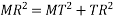
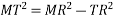
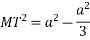
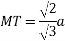
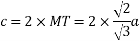
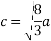
Lattice
A lattice is a par in (L, S) in which every {a, b} consisting of two elements has at least upper bound and a greatest lower band.
LUB {a, b} is denoted by 
is called the join of a and b.
aLB {a, b} is denoted by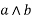 
is called the meet of a and b.
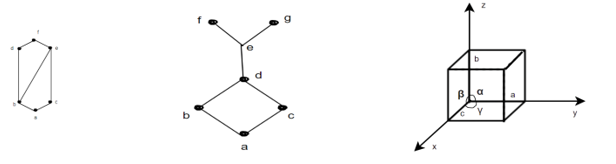Diagram (a) is lattice.
Diagram (b) is not a lattice as feg doesn't exist.
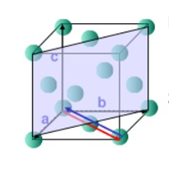
Lattice Parameters: -
It refers to the physical dimension of unit cell in a crystal lattice. In 3- dimension there are generally three lattice constants referred to as a, b, c (in diagram (c)).
A group of lattice constant code referred to as lattice parameters however the full set of 3 lattice constant three angles between them.
Example: - The lattice constant for diamond is at 300 k.
The structure is equal and but still its actual shape cannot be determined from only lattice constant.
Properties of lattice: -
1) Idempotent lattice property: - a)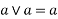 
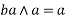
2) Commutative property: - a)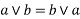 
3) Associative property: -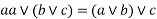
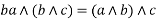
4) Absorption property: - a)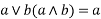 
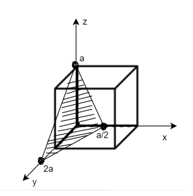
Miller Indices: = Identifying a particular plane or surface in a 3-dimensional crystal using set of numbers.
Procedure: -
(1)
(x, y, z) =
(x, y, z) pu=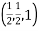
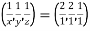
Remove common factor or common number in the denominator then we get Miller Indices.
Therefore, miller indices are (2,2,1)
(2)
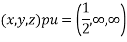
Hence Miller indices = (2, 0, 0)
(3)
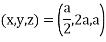
Miller indices = (4, 1, 2)
(4)
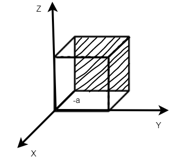
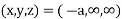
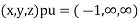
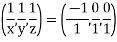
Miller indices = (-1, 0, 0)
Crystal imperfections: - Crystal imperfections are the defects in the regular geometrical arrangement of the atom in a crystalline solid.
The defects may lead to the crystal the formation or else rapid cooling from higher temperature or high energy radiation striking the solid.
these defects directly impact on its mechanical, electrical and optical behaviors of the crystal.
Different types of defects in single atomic crystalline structure: -
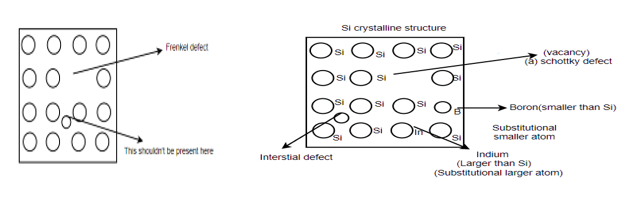
Schottky defect: - A vacancy or vacancies in an ionic crystal structures are called Schottky defect.
Interstitial defect: - atoms that occupy a site in the crystal structure at which there is usually not an atom.
Frenkel defect: - nearby peer of vacancy and an interstitial is called as Frenkel defect.
Substitutional defect: - if different atoms are occupying the locations of the regular atom, then they are called substitutional defect.
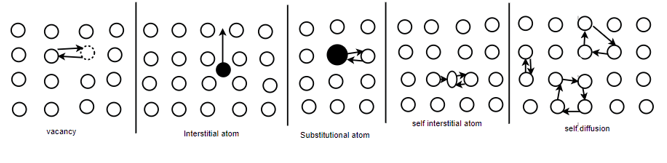
Diffusion mechanism: -
In pure metals self-diffusion occurs where there is no net mass transport, but atoms migrate in a random manner throughout the crystal.
The most energetically favourable process involves and interchange of places by an atom and a neighbouring vacancy - vacancy diffusion. This process demands not only the motion of vacancies, but also the presence of vacancies. The unit step in vacancy diffusion is an atom breaks its bonds and jump into neighbouring vacant site. In interstitial diffusion, solute atoms which are small enough to occupy interstitial sites defuse by jumping from one interstitial site to another. the unit step hair involves jump off the diffusing atom from one interstitial site to a neighbouring site. Substitutional diffusion generally proceeds by the vacancy mechanism. Thus, interstitial diffusion is faster than the substitutional diffusion by the vacancy mechanism.
Self-diffusion or Ring mechanism for direct exchange mechanism, hair three or four atoms in the form of a ring move simultaneously round the ring there by interchanging their positions.
A self-interstitial is more mobile than a vacancy as only small activation energy is required to move to an equilibrium atomic position and simultaneously displays the neighbouring atom into an interstitial site.
Directions
Consider a crystal lattice with unit cell edges a, b and c. A crystal direction [uvw] is parallel to the direction joining the origin of the crystal lattice with the point with coordinates (ua, vb, wc)
Procedure:
1 Any line or vector direction is specified by 2 points. The first pt. is typically at the origin (000)
2 Determine length of vector projection in each of 3 axes in units of fraction of a, b, c
X (a) Y(b) Z(c)
1 1 0
3. multiply or divide by a common factor to reduce the length of the smallest integer values
u v w.
4. Enclose in square brackets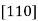 
direction.
5. Designate negative number by a bar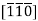 
pronounced bar 1 bar 1 zero direction.
6. family of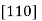 
direction is designated as <110>.
Planes
A plane with Miller indices (hkl) passes through the three points (a/h,0,0), (0, b/k,0) and (0,0, c/l) on the edges of the unit cell. The set of parallel lattice planes passes through all similar points in the lattice. The plane d-spacing is the perpendicular distance from the origin to the closest plane and also the perpendicular distance between successive planes. In materials with cubic symmetry the crystal direction [uvw] and the normal to the plane (uvw) are parallel.
Crystal planes come from the structures known as crystal lattices. These lattices are three-dimensional patterns that consist of symmetrically organized atoms intersecting three sets of parallel planes. These parallel planes are "crystal planes" and are used to determine the shape and structure of the unit cell and crystal lattice. The planes intersect with each other and make 3D shapes that have six faces. These crystal planes define the crystal structure by making axes visible and are the means by which we can calculate the Miller Indices.
Packing factor is the fraction of the volume of a unit cell that is occupied by "hard sphere" atoms or ions. It is the sum of the sphere volumes of all atoms within a unit cell (assuming the atomic hard-sphere model) divided by the unit cell volume. It is dimensionless and always less than unity.
Metals typically have relatively large atomic packing factors to maximize the shielding provided by the free electron cloud. Hexagonal close-packed and face-centered cubic structures have maximum packing factor and are more able to resist deformation.
Packing factor is also known as atomic packing factor (APF), packing efficiency or packing fraction.
The packing factors of slip systems include:
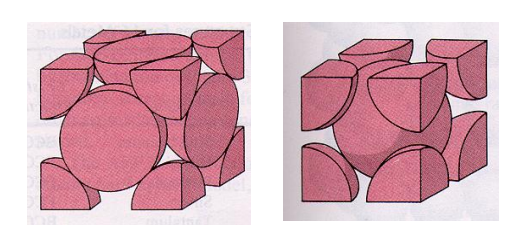
To calculate the particle packing density the spheres in the unit cell are counted up. The body-centered cubic structure contains (1 + 8·⅛ = 2) formula units per cell; the face-centered cubic unit cell contains (6·½ + 8·⅛ = 4) formula units, giving it the higher packing density. To determine the packing efficiency, we proceed as follows (all spheres are identical in size): If the edge length of the cubic cell is a, then the volume of the cell is: V = a 3.
In the case of the body-centered structure, the radius of the spheres is exactly ¼ of the body diagonal of the cube; for the face-centered cubic structure it is exactly ¼ of the diagonal of the face. This results in the following packing efficiencies:
Problem: Calculate the packing density of the body centered cubic, the face centered cubic and the diamond lattice, listed in example 2.1 p 28. Solution
Sol: The packing density is calculated as in example 2.1 p 28 and obtained from:
The correct radius and number of atoms per unit cell should be used.
A body centered cubic lattice contains an additional atom in the middle and therefore contains two atoms per unit cell. The atoms touch along the body diagonal, which equals 3 a. The radius is one quarter of the body diagonal.
A face centered cubic lattice contains six additional atoms in the center of all six faces of the cube. Since only half of the atoms is within the cube the total number of atoms per unit cell equals four. The atoms touch along the diagonal of the faces of the cube, which equals 2 a. The radius is one quarter of the diagonal.
The diamond lattice contains two face centered cubic lattice so that the total number of atoms per unit cell equals twice that of the face centered lattice, namely eight. The atoms touch along the body diagonal, where two atoms are one quarter of the body diagonal apart or 3 a / 4. The radius equals half the distance between the two atoms.
The radius, number of atoms per unit cell and the packing density are summarized in the table below.
| Radius | Atoms/ unit cell | Packing density |
Simple cubic
Body centered cubic
Face centered cubic
Diamond |  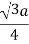 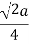 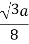 | 1
2
4
8
|    
|
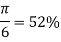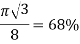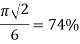
Voids literally mean gaps between the constituent particles. Voids in solid states mean the vacant space between the constituent particles in a closed packed structure. Close packing in solids can be generally done in three ways: 1D close packing, 2D close packing and 3D close packing. In 2 dimensional structures when the atoms are arranged in square close packing and hexagonal close packing, we see empty spaces left over between the atoms. These empty spaces are called voids and in the case of hexagonal packing, these voids are in triangular shapes and are known as the triangular voids.
The size and distribution of voids in materials plays a role in determining in the close packed crystals (FCC, HCP) there are two types of voids
- tetrahedral and octahedral voids (identical in both the structures as the voids are formed between two layers of atoms).
Technically important properties such as mechanical strength. Ductility’ Crystal growth, magnetic hysteresis, dielectric strength, conduction in Semiconductors are greatly affected by relatively minor changes in crystal Structure caused by DEFECTS/ IMPERFECTIONS
Crystal Imperfections are the defects in the regular geometrical arrangement of the atoms in a Crystalline solid. A Perfect Crystal is an idealization; there is no such thing in nature.
The defects may be the results of the crystal deformation or rapid cooling from high temperature or high energy radiation striking the solid. The defects influence the mechanical, electrical, and optical behaviour of the crystal
The imperfections may be classified widely as:
References:
1. Materials Science and Engineering by V.Raghavan, Prentice Hall of India Pvt.Ltd.
2. Elements of Materials Science & Engineering by Van Vlack, Pearson
3. Mechanical Metallurgy by Dieter, Tata MacGraw Hill
4. Composite Material science and Engineering by K. K. Chawla, Springer
5. Material Science and Metallurgy, by U. C. Jindal, Pearson
