Unit - 4
Friction Effects
The screw jack is a device, for lifting heavy loads, by applying a comparatively smaller effort at its handle. The principle, on which a screw jack works is similar to that of an inclined plane
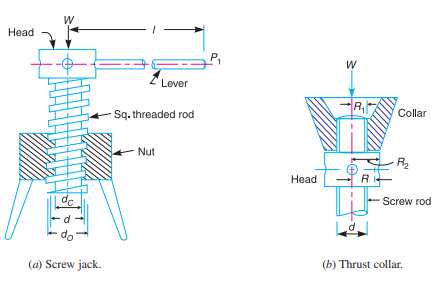
Fig. (a) shows a common form of a screw jack, which consists of a square threaded rod (also called screw rod or simply screw) which fits into the inner threads of the nut. The load, to be raised or lowered, is placed on the head of the square threaded rod which is rotated by the application of an effort at the end of the lever for lifting or lowering the load.
Torque Required to Lift the Load by a Screw Jack:
If one complete turn of a screw thread by imagined to be unwound, from the body of the screw and developed, it will form an inclined plane as shown in Fig. 10.12 (a).
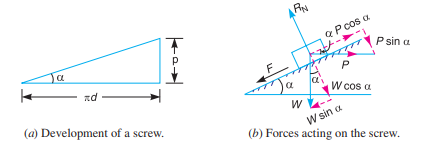
p = Pitch of the screw,
d = Mean diameter of the screw,
α = Helix angle,
P = Effort applied at the circumference of the screw to lift the load,
W = Load to be lifted, and
µ = Coefficient of friction, between the screw and nut = tan φ, where φ is the friction angle.
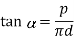
Since the principle on which a screw jack works is similar to that of an inclined plane, therefore the force applied on the lever of a screw jack may be considered to be horizontal as shown in Fig. 10.12 (b). Since the load is being lifted, therefore the force of friction (F = µ. RN) will act downwards. All the forces acting on the screw are shown in Fig. 10.12 (b). Resolving the forces along the plan
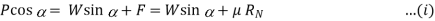
And resolving the forces perpendicular to the plane
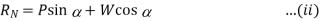
Substituting this value of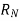 
in equation (i)
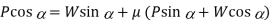
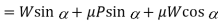
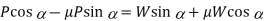
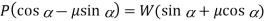
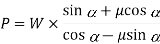
Substituting the value of µ = tan φ in the above equation, we get
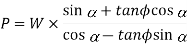
Multiplying the numerator and denominator by cos φ,
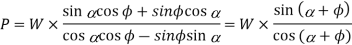
∴ Torque required to overcome friction between the screw and nut
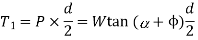
When the axial load is taken up by a thrust collar or a flat surface, as shown in Fig. 10.11 (b), so that the load does not rotate with the screw, then the torque required to overcome friction at the collar,
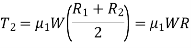
R1 and R2 = Outside and inside radii of the collar, R = Mean radius of the collar, and µ1 = Coefficient of friction for the collar. ∴ Total torque required to overcome friction (i.e., to rotate the screw)
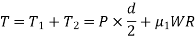
If an effort P1 is applied at the end of a lever of arm length l, then the total torque required to overcome friction must be equal to the torque applied at the end of the lever, i.e.
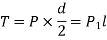
When the *nominal diameter (d0) and the **core diameter (dc) of the screw thread is given, then the mean diameter of the screw
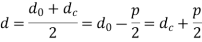
Since the mechanical advantage is the ratio of load lifted (W) to the effort applied (P1) at the end of the lever, therefore mechanical advantage,
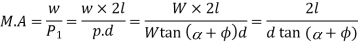
The rotating shafts are frequently subjected to axial thrust. The bearing surfaces such as pivot and collar bearings are used to take this axial thrust of the rotating shaft. The propeller shafts of ships, the shafts of steam turbines, and vertical machine shafts are examples of shafts which carry an axial thrust.
The bearing surfaces placed at the end of a shaft to take the axial thrust are known as pivots. The pivot may have a flat surface or conical surface as shown in Fig. 10.16 (a) and (b) respectively. When the cone is truncated, it is then known as truncated or trapezoidal pivot as shown in Fig. 10.16 (c).
The collar may have flat bearing surface or conical bearing surface, but the flat surface is most commonly used. There may be a single collar, as shown in Fig. 10.16 (d) or several collars along the length of a shaft, as shown in Fig. 10.16 (e) in order to reduce the intensity of pressure.
In modern practice, ball and roller thrust bearings are used when power is being transmitted and when thrusts are large as in case of propeller shafts of ships.
Single Disc or Plate Clutch:
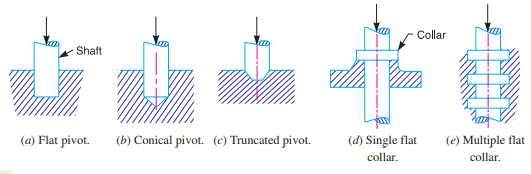
A single disc or plate clutch, as shown in Fig. 10.21, consists of a clutch plate whose both sides are faced with a friction material (usually of Ferrodo). It is mounted on the hub which is free to move axially along the splines of the driven shaft. The pressure plate is mounted inside the clutch body which is bolted to the flywheel. Both the pressure plate and the flywheel rotate with the engine.
crankshaft or the driving shaft. The pressure plate pushes the clutch plate towards the flywheel by a set of strong springs which are arranged radially inside the body. The three levers (also known as release levers or fingers) are carried on pivots suspended from the case of the body. These are arranged in such a manner so that the pressure plate moves away from the flywheel by the inward movement of a thrust bearing. The bearing is mounted upon a forked shaft and moves forward when the clutch pedal is pressed.
When the clutch pedal is pressed down, its linkage forces the thrust release bearing to move in towards the flywheel and pressing the longer ends of the levers inward. The levers are forced to turn on their suspended pivot and the pressure plate moves away from the flywheel by the knife edges, thereby compressing the clutch springs. This action removes the pressure from the clutch plate and thus moves back from the flywheel and the driven shaft becomes stationary. On the other hand, when the foot is taken off from the clutch pedal, the thrust bearing moves back by the levers. This allows the springs to extend and thus the pressure plate pushes the clutch plate back towards the flywheel.
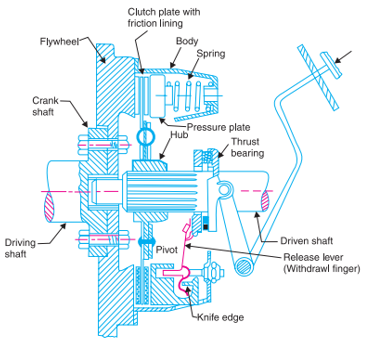
The axial pressure exerted by the spring provides a frictional force in the circumferential direction when the relative motion between the driving and driven members tends to take place. If the torque due to this frictional force exceeds the torque to be transmitted, then no slipping takes place and the power is transmitted from the driving shaft to the driven shaft. Now consider two friction surfaces, maintained in contact by an axial thrust W, as shown in
T = Torque transmitted by the clutch,
p = Intensity of axial pressure with which the contact surfaces are held together
r 1 and r 2 = External and internal radii of friction faces, and
µ = Coefficient of friction. Consider an elementary ring of radius r and thickness dr as shown in Fig. We know that area of contact surface or friction surface, = 2 π r. dr
∴ Normal or axial force on the ring,
δW = Pressure × Area = p × 2 π r. dr
and the frictional force on the ring acting tangentially at radius r,
Fr = µ. δW = µ. p × 2 π r. dr
∴ Frictional torque acting on the ring,
Tr = Fr × r = µ. p × 2 π r. dr × r = 2 π × µ. p.r 2 d
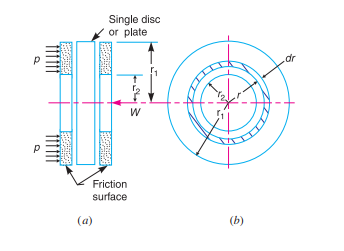
We shall now consider the following two cases:
1. When there is a uniform pressure, and
2. When there is a uniform wear.
1. Considering uniform pressure When the pressure is uniformly distributed over the entire area of the friction face, then the intensity of pressure,
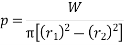
W = Axial thrust with which the contact or friction surfaces are held together. We have discussed above that the frictional torque on the elementary ring of radius r and thickness dr is.
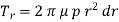
Integrating this equation within the limits from r 2 to r 1 for the total frictional torque
∴ Total frictional torque acting on the friction surface or on the clutch,
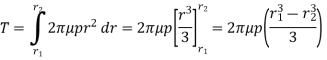
Substituting the value of p from equation (i),
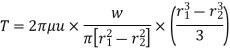
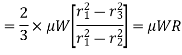
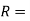Mean radius of friction surface
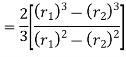
2. Considering uniform wear
In Fig., let p be the normal intensity of pressure at a distance r from the axis of the clutch. Since the intensity of pressure varies inversely with the distance, therefore
p.r. = C (a constant) or p = C/r ...(i)
and the normal force on the ring,
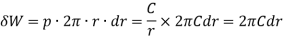
∴ Total force acting on the friction surface,
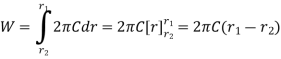
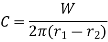
We know that the frictional torque acting on the ring,
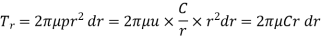
∴ Total frictional torque on the friction surface,
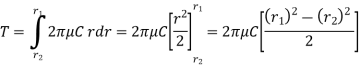
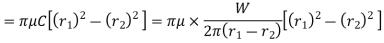
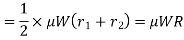
R = Mean radius of the friction surface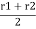 
Notes: 1. In general, total frictional torque acting on the friction surface (or on the clutch) is given by T = n.µ.W.R
n = Number of pairs of friction or contact surfaces, and
R = Mean radius of friction surface
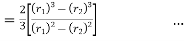(For uniform pressure)
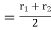… (For uniform wear)
2. For a single disc or plate clutch, normally both sides of the disc are effective. Therefore, a single disc clutch has two pairs of surfaces in contact, i.e., n = 2.
3. Since the intensity of pressure is maximum at the inner radius (r 2) of the friction or contact surface, therefore equation (i) may be written as
pmax × r 2 = C or pmax = C/r 2
4. Since the intensity of pressure is minimum at the outer radius (r 1) of the friction or contact surface, therefore equation (i) may be written as
pmin × r 1 = C or pmin = C/r1
5. The average pressure (pav) on the friction or contact surface is given by
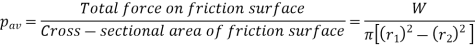
6. In case of a new clutch, the intensity of pressure is approximately uniform but in an old clutch the uniform wear theory is more approximate.
7. The uniform pressure theory gives a higher frictional torque than the uniform wear theory. Therefore, in case of friction clutches, uniform wear should be considered,
unless otherwise stated.
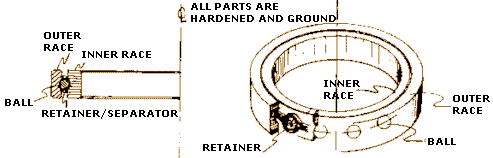
An antifriction bearing is a bearing that contains moving elements to provide a low friction support surface for rotating or sliding surfaces. Antifriction bearings are commonly made with hardened rolling elements (balls and rollers) and races. A race is the bearing surface in an antifriction bearing that supports rolling elements during rotation. A separator is an antifriction bearing component used to maintain the position and alignment of rolling elements. Antifriction bearings reduce lubrication requirements and decrease starting and operating friction. Reduced friction results in less power required to rotate engine components and increases overall engine output.
The crankshaft is supported by main bearings. A main bearing is a bearing that supports and provides a low-friction bearing surface for the crankshaft. Small engines commonly have two main bearings, one at each end of the crankshaft. Small engines with three or more cylinders may require more than two main bearings to provide additional support to the crankshaft. Main bearings are mounted in the crankcase and can be either friction or antifriction bearings. Antifriction bearings used for main bearings increase the radial and axial load capacity of the engine but also contributes to engine noise and are more costly than journal bearings.
4.5 Film friction
Fluid friction (or film friction or viscous friction).
It is the friction, experienced between the rubbing surfaces, when the surfaces have a thick layer of the lubricant. In this case, the actual surfaces do not come in contact and thus do not rub against each other. It is thus obvious that fluid friction is not due to the surfaces in contact but it is due to the viscosity and oiliness of the lubricant.
Note: The viscosity is a measure of the resistance offered to the sliding one layer of the lubricant over an adjacent layer. The absolute viscosity of a lubricant may be defined as the force required to cause a plate of unit area to slide with unit velocity relative to a parallel plate, when the two plates are separated by a layer of lubricant of unit thickness.
The oiliness property of a lubricant may be clearly understood by considering two lubricants of equal viscosities and at equal temperatures. When these lubricants are smeared on two different surfaces, it is found that the force of friction with one lubricant is different than that of the other. This difference is due to the property of the lubricant known as oiliness. The lubricant which gives lower force of friction is said to have greater oiliness.
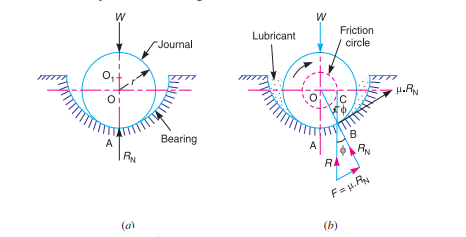
A journal bearing forms a turning pair as shown in Fig. 10.15 (a). The fixed outer element of a turning pair is called a bearing and that portion of the inner element (i.e., shaft) which fits in the bearing is called a journal. The journal is slightly less in diameter than the bearing, in order to permit the free movement of the journal in a bearing.
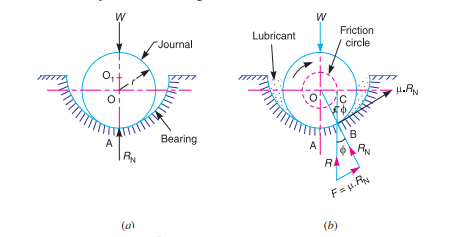
When the bearing is not lubricated (or the journal is stationary), then there is a line contact between the two elements as shown in Fig. (a). The load W on the journal and normal reaction RN (equal to W) of the bearing acts through the centre. The reaction RN acts vertically upwards at point A. This point A is known as seat or point of pressure.
Now consider a shaft rotating inside a bearing in clockwise direction as shown in Fig. (b). The lubricant between the journal and bearing forms a thin layer which gives rise to a greasy friction. Therefore, the reaction R does not act vertically upward, but acts at another point of pressure B. This is due to the fact that when shaft rotates, a frictional force F = µ RN acts at the circumference of the shaft which has a tendency to rotate the shaft in opposite direction of motion and this shifts the point A to point B. In order that the rotation may be maintained, there must be a couple rotating the shaft. Let
φ = Angle between R (resultant of F and RN) and RN
, µ = Coefficient of friction between the journal and bearing,
T = Frictional torque in N-m, and
r = Radius of the shaft in metres.
For uniform motion, the resultant force acting on the shaft must be zero and the resultant turning moment on the shaft must be zero. In other words,
R = W, and T = W × OC = W × OB sin φ = W.r sin φ
Since φ is very small, therefore substituting sin φ = tan φ ∴
T = W.r tan φ = µ.W.r ... (∵ µ = tan φ)
If the shaft rotates with angular velocity ω rad/s, then power wasted in friction,
P = T.ω = T × 2πN/60 watts where
N = Speed of the shaft in r.p.m.
For a turning pair (Shaft and Journal or Pin and Bearing) it is assumed that contact is along the axial line and that the total reaction will pass through the position of contact. Diagram (a) shows the forces when the shaft is at rest.
It is assumed that there is no friction and the only two forces are P and the reaction R. When movement occurs, the Total Reaction must be inclined at the Friction angle and this can only be achieved if the Point of Contact moves to a position as shown in Diagram (b). As Friction must oppose movement the Point of Contact will move around the Pin against the Direction of Motion.
Types of Belts Drives: The belt drives are usually classified into the following three groups:
1. Light drives. These are used to transmit small powers at belt speeds up to about 10 m/s, as in agricultural machines and small machine tools.
2. Medium drives. These are used to transmit medium power at belt speeds over 10 m/s but up to 22 m/s, as in machine tools.
3. Heavy drives. These are used to transmit large powers at belt speeds above 22 m/s, as in compressors and generators. 11.4
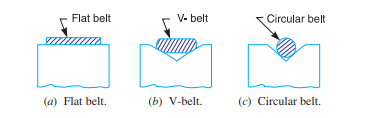
Types of Belts
1. Flat belt. The flat belt, as shown in Fig. 11.1 (a), is mostly used in the factories and workshops, where a moderate amount of power is to be transmitted, from one pulley to another when the two pulleys are not more than 8 metres apart.
2. V-belt. The V-belt, as shown in Fig. 11.1 (b), is mostly used in the factories and workshops, where a moderate amount of power is to be transmitted, from one pulley to another, when the two pulleys are very near to each other.
3. Circular belt or rope. The circular belt or rope, as shown in Fig. 11.1 (c), is mostly used in the factories and workshops, where a great amount of power is to be transmitted, from one pulley to another, when the two pulleys are more than 8 meters apart.
Rope Drive:
The rope drives are widely used where a large amount of power is to be transmitted, from one pulley to another, over a considerable distance. It may be noted that the use of flat belts is limited for the transmission of moderate power from one pulley to another when the two pulleys are not more than 8 metres apart. If large amounts of power are to be transmitted by the flat belt, then it would result in excessive belt cross-section. It may be noted that frictional grip in case of rope drives is more than that in V-drive. One of the main advantages of rope drives is that a number of separate drives may be taken from the one driving pulley. For example, in many spinning mills, the line shaft on each floor is driven by ropes passing directly from the main engine pulley on the ground floor. The rope drives use the following two types of ropes: 1. Fibre ropes, and 2. Wire ropes. The fibre ropes operate successfully when the pulleys are about 60 metres apart, while the wire ropes are used when the pulleys are up to 150 metres apart.
Chain Drives:
We have seen in belt and rope drives that slipping may occur. In order to avoid slipping, steel chains are used. The chains are made up of rigid links which are hinged together in order to provide the necessary flexibility for warping around the driving and driven wheels. The wheels have projecting teeth and fit into the corresponding recesses, in the links of the chain as shown in Fig. 11.23. The wheels and the chain are thus constrained to move together without slipping and ensures perfect velocity ratio.
The toothed wheels are known as sprocket wheels or simply sprockets. These wheels resemble to spur gears.
The chains are mostly used to transmit motion and power from one shaft to another, when the distance between the centres of the shafts is short such as in bicycles, motor cycles, agricultural machinery, road rollers, etc
4.9 Initial tension
When a belt is wound round the two pulleys (i.e., driver and follower), its two ends are joined together; so that the belt may continuously move over the pulleys, since the motion of the belt from the driver and the follower is governed by a firm grip, due to friction between the belt and the pulleys. In order to increase this grip, the belt is tightened up. At this stage, even when the pulleys are stationary, the belt is subjected to some tension, called initial tension.
When the driver starts rotating, it pulls the belt from one side (increasing tension in the belt on this side) and delivers it to the other side (decreasing the tension in the belt on that side). The increased tension in one side of the belt is called tension in tight side and the decreased tension in the other side of the belt is called tension in the slack side
Let T0 = Initial tension in the belt,
T1 = Tension in the tight side of the belt
T2 = Tension in the slack side of the belt, and
α = Coefficient of increase of the belt length per unit force.
A little consideration will show that the increase of tension in the tight side
= T1 – T0
and increase in the length of the belt on the tight side
= α (T1 – T0) ...(i)
Similarly, decrease in tension in the slack side
= T0 – T2
and decrease in the length of the belt on the slack side
= α (T0 – T2) ...(ii)
Assuming that the belt material is perfectly elastic such that the length of the belt remains constant, when it is at rest or in motion, therefore increase in length on the tight side is equal to decrease in the length on the slack side. Thus, equating equations (i) and (ii),
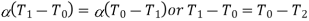
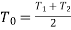…(Neglecting centrifugal tension)
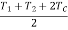…(Considering centrifugal tension)
Centrifugal Tension
Since the belt continuously runs over the pulleys, therefore, some centrifugal force is caused, whose effect is to increase the tension on both, tight as well as the slack sides. The tension caused by centrifugal force is called centrifugal tension. At lower belt speeds (less than 10 m/s), the centrifugal tension is very small, but at higher belt speeds (more than 10 m/s), its effect is considerable and thus should be taken into account.
Consider a small portion PQ of the belt subtending an angle dθ the centre of the pulley as shown in Fig. 11.17
Let m = Mass of the belt per unit length in kg,
v = Linear velocity of the belt in m/s,
r = Radius of the pulley over which the belt runs in metres, and
TC = Centrifugal tension acting tangentially at P and Q in newtons.
We know that length of the belt PQ
= r. dθ
and mass of the belt PQ = m. r. dθ
∴ Centrifugal force acting on the belt PQ, 2
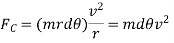
The centrifugal tension TC acting tangentially at P and Q keeps the belt in equilibrium. Now resolving the forces (i.e., centrifugal force and centrifugal tension) horizontally and equating the same, we have
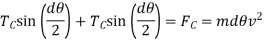
Since the angle dθ is very small, therefore, putting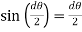 
the above expression,
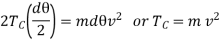
When the centrifugal tension is taken into account, then total tension in the tight side, Tt1 = T1 + TC
and total tension in the slack side,
Tt2 = T2 + TC
2. Power transmitted, P = (Tt1 – Tt2) v ... (in watts)
= [(T1 + TC) – (T2 + TC)] v
= (T1 – T2) v ... (same as before)
Thus, we see that centrifugal tension has no effect on the power transmitted. 3. The ratio of driving tensions may also be written as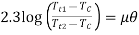 
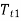= Maximum or total tension in the belt.
Maximum Power Transmitted: The power transmitted depends on the tension ‘T1’, angle of lap , coefficient of friction ‘’ and belt speed ‘V’. For a given belt drive, the maximum tension (Tt), angle of lap and coefficient of friction shall remain constant provided that
(a) the tension on tight side, i.e., maximum tension should be equal to the maximum permissible value for the belt, and
(b) the belt should be on the point of slipping.
Therefore, Power 1 P T e (1) V
Since, T1=Tt +Tc
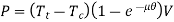
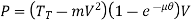
For maximum power transmitted
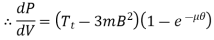
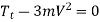
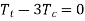
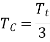
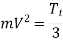
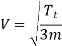
Slip of the belt A firm frictional grip between belt and shaft is essential. But sometimes it becomes insufficient. This may cause some forward motion of the belt without carrying the driven pulley with it. This called as slip of the belt. It is expressed as a percentage.
Effect on velocity ratio: Result of belt slipping is to reduce the velocity ratio of the system.
Creep in belt drive: When the belt passes from slack side to tight side, a certain portion of the belt extends and it contracts again when the belt passes from tight sight to slack side. Due to these changes in length, there is a relative motion between the belt and the pulley surfaces. This relative motion is called as creep.
Effect on velocity ratio: The total effect of creep is to reduce slightly the speed of the driven pulley or follower.
References:
