UNIT-4

Partial differential equation: First order

4.1 Order and Degree

A differential equation involving partial derivatives with respect to more than one independent variable is called a partial differential equation.

The independent variables will be denoted by x and y and the dependent variable by z. The partial differential coefficients are denoted as-

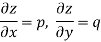
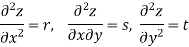
ORDER of a partial differential equation is the same as that of the order of the highest differential coefficient in it.

Classification of partial differential equation-

Suppose the equation is-

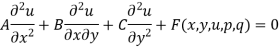
Here A, B, C are the constants of x and y, then the equation-

1. Elliptical- if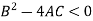

2. Parabolic- if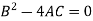

3. Hyperbolic- if if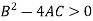

Order of a differential equation:

The order of the highest derivative involved in the differential equation i.e. how many times it is differentiated is called the order of the differential equation.

Degree of the differential equation:

The degree of the highest derivative involved in the differential equation after made free from radicals and fractions as far as derivatives are concerned i.e.  power of the highest derivative is called  the degree of the differential equation.

Example: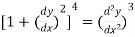 has order 2 and degree 3.

Types of Differential equations:

Ordinary Differential Equation:

A differential equation involving derivatives with respect to single independent variables is called ordinary differential equation.

Example: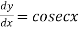 

Partial Differential Equation:

A differential equation involving derivatives with respect to more than one independent variable is called partial differential equation.

Example: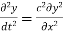

Linear and Non-linear differential equations:

A differential equation is linear if

1. Every dependent variable and every derivatives present in the equation is only of degree one.
2. No products of dependent variables or derivatives occur in the equation.

Otherwise it is a non-linear equation.

Solution of differential equations:

A relation between the dependent variable and independent variables which satisfies the given differential equation is called the solution or the integral of the differential equation.

Example: The relation 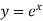    is the solution of .

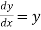General solution, Particular   solution and Singular solution:

Let 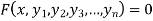….(i)

Be an nth order ordinary differential equation.

General Solution: A solution of (i) which contain n arbitrary constants is called general solution.

Particular Solution: A solution of (i) which is obtained by substituting particular values to the one or more n arbitrary constants is called the particular solution.

Singular solution: A solution which cannot be obtained from the general solution.

4.2 Formation, Linear Partial differential equations of First order

Formation of partial differential equation-

Method of elimination of arbitrary constants-

Example: Form a partial differential equation from-

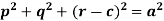
Sol.

Here we have-

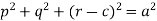
It contains two arbitrary constants a and c

Differentiate the equation with respect to p, we get-

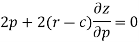
Or

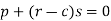
Now differentiate the equation with respect to q, we get-

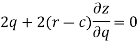
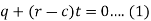
Now eliminate ‘c’,

We get

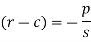
Now put z-c in (1), we get-

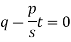
Or

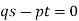
The second method we use is method of elimination of arbitrary function.

Solution of partial differential equation by direct partial Integration-

Example: Solve-

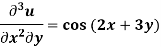
Sol.

Here we have-

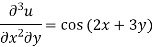
Integrate w.r.t. x, we get-

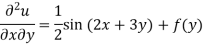
Integrate w.r.t. x, we get-

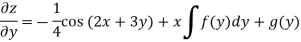
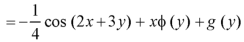
Integrate w.r.t. y, we get-

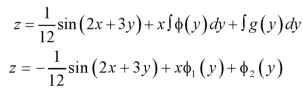
Example: Solve the differential equation-

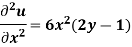
Given the boundary condition that-

At x = 0,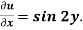

Sol.

Here we have-

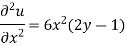
On integrating partially with respect to x, we get-

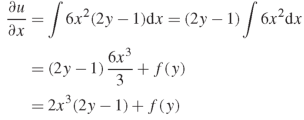
Here f(y) is an arbitrary constant.

Now form the boundary condition-

When x = 0,

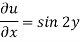
Hence-

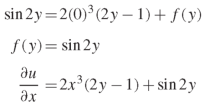
On integrating partially w.r.t. x, we get-

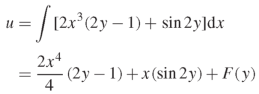
Example: Solve the differential equation-

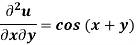
Given that 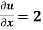when y = 0, and u = 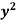when x = 0.

Sol.

We have-

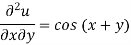
Integrating partially w.r.t. y, we get-

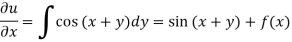
Now from the boundary conditions,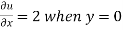

Then-

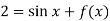
From which,

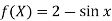
It means,

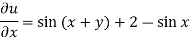
On integrating partially w.r.t. x givens-

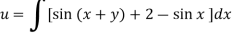
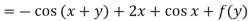
From the boundary conditions, u = 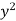when x = 0

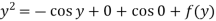
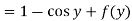
From which-

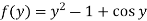
Therefore the solution of the given equation is-

4.3 Lagrange’s Form

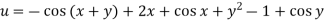
Linear Equations of the First Order

A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the form

Pp + Qq = R              (1)

Where, P, Q and R are functions of x, y, z. This equation is called a quast linear equation. When P, Q and R are independent of z it is known as linear equation.

Such asn equation is obtained by eliminating an arbitrary function 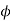from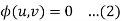

Where u,v are are some functions of x, y, z.

Differentiating (2) partially with respect to x and y

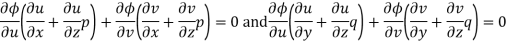
Eliminating 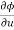and 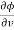, we get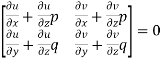

Which simplifies to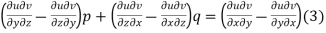

This is of the same form as (1)

Now suppose u = a and v=b, where a, b are constants, so that

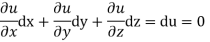
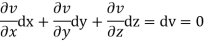
By cross multiplication we have,

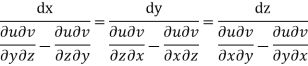
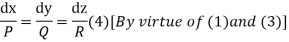
The solution of these equations are u = a and v = b

Therefore, 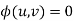is the required solution of (1).

Thus to solve the equation Pp + Qq =R.

(i) form the subsidiary equations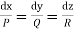

(ii) Solve these simultaneous equations

(iii) Write the complete solution as 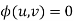or u=f(v)

Method of multipliers-

Let the auxiliary equation be

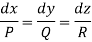
L, m, n may be the constants of x, y, z then we have-

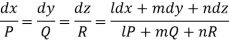
L, m, n are selected in a such a way that-

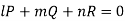
Thus

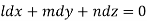
On solving this differential equation, if the solution is- u =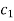

Similarly, choose another set of multipliers 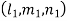and if the second solution is v =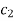

So that the required solution is f(u, v) = 0.

Example. Solve 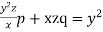   (Kottayam, 2005)

Solution. Rewriting the given equation as

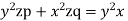
The subsidiary equations are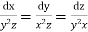

The first two fractions give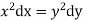

Integrating we get 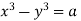   n    (i)

Again the first and third fraction give xdx = zdz

Integrating, we get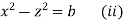

Hence from (i) and (ii), the complete solution is

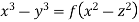
Example. Solve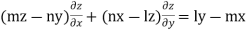

Solution. Here the subsidiary equations are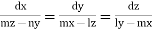

Using multipliers x,y, and z we get each fraction =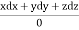

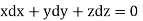which on integration gives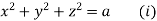

Again using multipliers l, m and n we get each fraction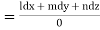

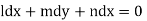which on integration gives lx +my +nz = b     (ii)

Hence from (i) and (ii) the required solution is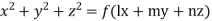

Example. Solve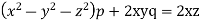

Solution. Here the subsidiary equations are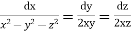

From the last two fractions, we have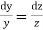

Which on integration gives log y = log z + log a or y/z=a     (i)

Using multipliers x, y and z we have

Each fraction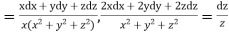

Which on integration gives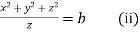

Hence from (i) and (ii) the required solution is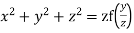

Example: Solve-

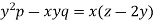
Sol.

We have-

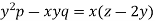
Then the auxiliary equations are-

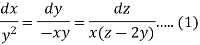
Consider first two equations only-

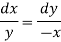
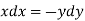
On integrating

…….. (2)

Now consider last two equations-

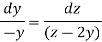
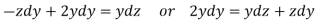
On integrating we get-

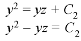…………… (3)

From equation (2) and (3)-

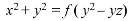
Example: Find the general solution of-

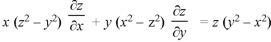
Sol. The auxiliary simultaneous equations are-

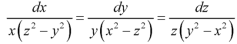……….. (1)

Using multipliers x, y, z we get-

Each term of (1) is equals to-

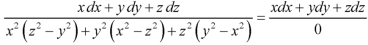
Xdx + ydy + zdz=0

On integrating-

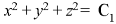………… (2)

Again equation (1) can be written as-

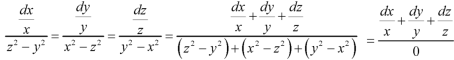
Or

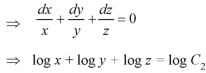
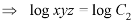
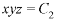………….. (3)

From (2) and (3), the general solution is-

4.4 Non Linear Partial Differential equations of first order

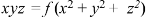
Non-linear partial differential equations-

Type-1: Equation of the type f(p, q) = 0

Method-

Let the required solution is-

Z = ax + by + c …….. (1)

So that-

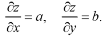
On putting these values in f(p, q) = 0

We get-

f(a, b) = 0

So from this, find the value of b in terms of a and put the value of b in (1). It will be the required solution.

Type-2: Equation of the type-

Z = px + qy + f(p, q)

Its solution will be-

Z = ax + by + f(a, b)

Type-3: Equation of the type f(z, p, q) = 0

Type-4: Equation of the type-

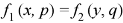
Method-

Let-

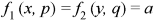
Example: Solve-

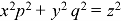
Sol.

This equation can be transformed as-

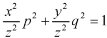
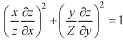
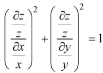………. (1)

Let

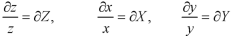
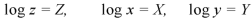
Equation (1) can be written as-

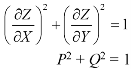………… (2)

Let the required solution be-

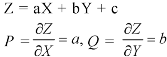
From (2) we have-

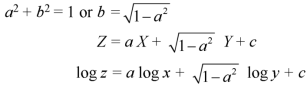
Example: Solve-

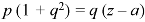
Sol.

Let u = x + by

So that-

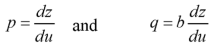
Put these values of p and q in the given equation, we get-

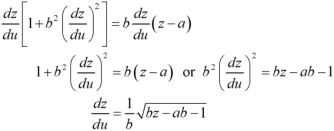
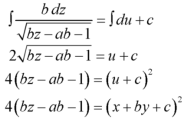
Example: Solve-

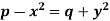
Sol.

Let-

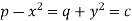
That means-

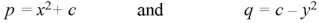
Put these values of p and q in

4.5 Charpit’s method, Standard forms

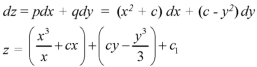
This is the general method for finding the complete integral of a non-linear partial differential equation.

Let us consider the equation-

f(x, y, z , p, q) = 0 ………. (1)

Since z depends on x and y, we have-

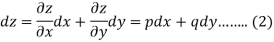
The main thing in Charpit’s method is to find the another relationship between the variables x, y, z and p. q.

And let the relation be-

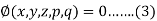
Here on solving equation (1) and (2), we get the values of p and q.

When we substitute these values of p and q in (2), it becomes integrable.

To determine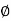, equation (1) and (3) are differentiated with respect to x and y.

We get, when we differentiate with respect to x,

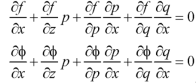
We get, when we differentiate with respect to y,

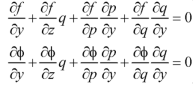
Eliminating 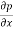between the equations we get from differentiating for x, we get

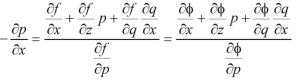
Or

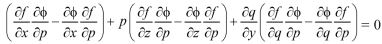…………(4)

Eliminating 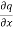between the equations we get from differentiating for y, we get

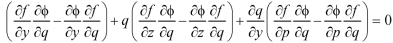…………(5)

Adding (4) and (5) and keeping in view the relation on, the terms of the last brackets of (4) and (5) cancel. On rearranging, we get-

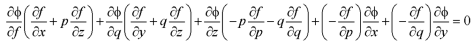
Or

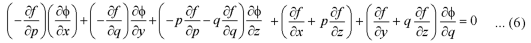
This equation is the Lagrange’s linear equation of the first order with x, y, z, p, q as independent variables and equation (4) as dependent variable.

Its subsidiary equations are-

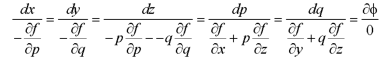
An integral of these equations involving p or q or both can be taken as the relation (3) which along with (1) will give the values of p and q to make (2) integrable.

Example: Solve-

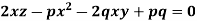
Sol.

Let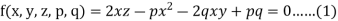
 

Charpit’s subsidiary equations are-

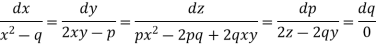
So that- dq = 0 or q = a

On putting q = a in (1) we get-

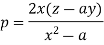
Such that-

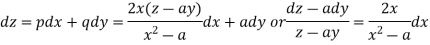
Integrating

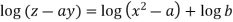
Or

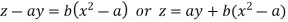
Which is the required solution.

Example: Solve-

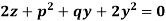
Sol.

Let

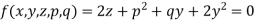
Charpit’s subsidiary equations are-

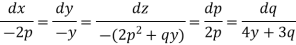
From the first and fourth ratios,

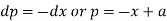
Substituting p = a – x in the given equation, we get-

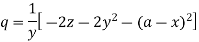
So that-

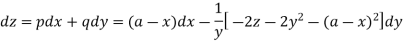
Multiply both sides by ,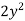

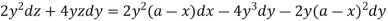
Integrating-

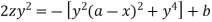
Or

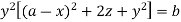
Which is the required solution.