UNIT 2

Number system

2.1 Data representations

Computer does not understand human language. Any data, viz., letters, symbols, pictures, audio, videos, etc., fed to computer should be converted to machine language first. Computers represent data in the following three forms −

Number System

We are introduced to concept of numbers from a very early age. To a computer, everything is a number, i.e., alphabets, pictures, sounds, etc., are numbers. Number system is categorized into four types −

• Binary number system consists of only two values, either 0 or 1
• Octal number system represents values in 8 digits.
• Decimal number system represents values in 10 digits.
• Hexadecimal number system represents values in 16 digits.

Bits and Bytes

Bits− A bit is a smallest possible unit of data that a computer can recognize or use. Computer usually uses bits in groups.

Bytes− group of eight bits is called a byte. Half a byte is called a nibble.

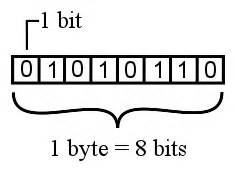
The following table shows conversion of Bits and Bytes −

Text Code

Text code is format used commonly to represent alphabets, punctuation marks and other symbols. Four most popular text code systems are −

• EBCDIC
• ASCII
• Extended ASCII
• Unicode

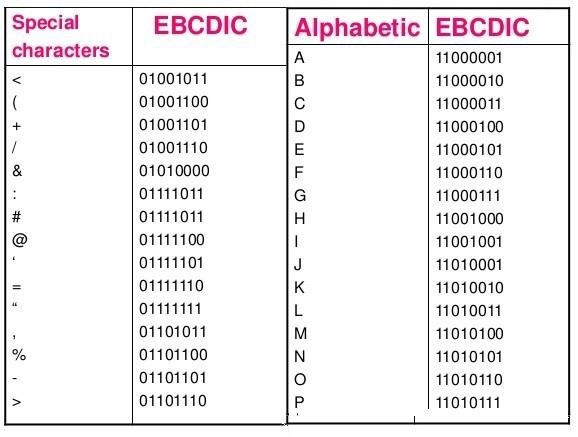
EBCDIC

Extended Binary Coded Decimal Interchange Code is an 8-bit code that defines 256 symbols. Given below is the EBCDIC Tabular column

ASCII

American Standard Code for Information Interchange is an 8-bit code that specifies character values from 0 to 127.

ASCII Tabular column

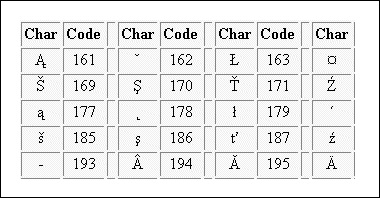
Extended ASCII

Extended American Standard Code for Information Interchange is an 8-bit code that specifies character values from 128 to 255.

Extended ASCII Tabular column

Unicode

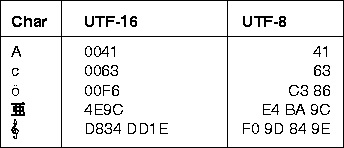
Unicode Worldwide Character Standard uses 4 to 32 bits to represent letters, numbers and symbol.

Unicode Tabular Column

2.2 Concepts of radix and representation of numbers in radix r with special cases of r=2, 8, 10 and 16 with conversion from radix r1 to r2, r’s and (r-1)’s complement

In number system modern method of representing numbers symbolically is based on positional notations.

In this method, each number is represented by a string of symbols where each symbol is associated with a specific weight depending upon its positions. The total number of different symbols which are used in a particular number system is called the base or radix of the system and the weight of each position of a particular number is expressed as a power of the base. When a number is formed with the combination of the symbols, each symbol is then called a digit and the position of each symbol is referred to as the digit position.

Thus if a number system has symbols starting from 0, and the digits of the system are 0, 1, 2, ….. (r - 1) then the base or radix is r. If a number D of this system be represented by

D = d₀ d₀……. d₀…….. d₁ d

then the magnitude of this number is given by

|D| = dn-1 rn-1 + dn-2 rn-2 + …… diri + …… d1 r1 + d0 r0

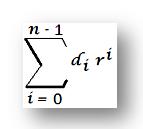
Where each d₀ ranges from 0 to r - 1, such that
0 ≤ d₀≤ r - 1, i = 0, 1, 2 ......(n - 1). 

The digit at the extreme left has the highest positional value and is generally called the Most Significant Digit, or in short MSD; similarly, the digit occupying the extreme right position has the least positional value and is referred to as the Least Significant Digit or LSD.

Radix Complement Representation:

In the decimal number system, the radix complement is the 10’s complement. In radix complement representation system, the complement of an n-digit number is obtained by subtracting the number from 10n.

Let us consider some examples of 3-digit numbers and their radix complement in decimal system.

br>From the above discussion we find that a subtraction operation is to be preformed to get the 10’s complement of a number, say, N. This subtraction operation can be avoided by rewriting 10n as (10n - 1) + 1 and 10n - N as {(10n - 1) - N} + 1. The number 10n - 1 is of the form 999...99 consisting of n digits. If the complement of a digit be defined as (9 - the concerned digit), then (10n - 1) - N is obtained by complementing the digits of N.

Therefore, the 10’s complement of the number N is obtained by subtracting each digit of the number from 9 and then adding 1 to the LSD of the number so formed.

For instance, the 10’s complement of 172 is (827 + 1) or 828 and that of 405 is (594 + 1) or 595.

For the binary number system the radix complement is the two’s complement. The 2’s complement of a binary number is obtained by subtracting each bit of the number from the radix diminished by 1 i.e. from (2 - 1) or 1 and adding an 1 to the LSB. The application of this rule is very simple. We have to just change 1 to 0 and 0 to 1 in every bit and then add 1 to the LSB of the number so formed. For example, the 2’s complement of the binary number 11011 is (00100 + 1) or 00101 and that of 10110 is (01001 + 1) or 01010.

If the number be in signed magnitude representation, it is positive if the MSB is 0 and negative if the MSB is 1. The decimal equivalent of a 2’s complement binary number, in the case of signed-magnitude representation, is computed in the same way as for an unsigned number except that the weight of the MSB is -2n-1 instead of +2n-1 for an n-bit binary number.

Let us observe some examples of 8-bit binary numbers and their 2’s complement are shown below:

Diminished Radix Complement Representation:

In the decimal number system the diminished radix complement is 9’s complement. This is obtained by subtracting each digit of the number from 9.

The diminished radix complement of binary numbers is called 1’s complement. The 1’s complement of a binary number is formed by replacing each 1 in the number by a 0 and each 0 by 1.

For example, 1’s complements of some binary numbers are;

In the case of signed magnitude representation of binary numbers, the MSB is the sign bit.

Positive number representations are same for both 1’s and 2’s complement. But representation of negative numbers differs by 1. A weight of -(2n-1 - 1) rather than -2n-1 is given to the MSB while computing the decimal equivalent of 1’s complement of a binary number.

A few examples of 8-bit binary numbers and their 1’s complement are given below;

Radix Complement Representation:

In the decimal number system, the radix complement is the 10’s complement. In radix complement representation system, the complement of an n-digit number is obtained by subtracting the number from 10n.

Let us consider some examples of 3-digit numbers and their radix complement in decimal system.

br>From the above discussion we find that a subtraction operation is to be preformed to get the 10’s complement of a number, say, N. This subtraction operation can be avoided by rewriting 10n as (10n - 1) + 1 and 10n - N as {(10n - 1) - N} + 1. The number 10n - 1 is of the form 999...99 consisting of n digits. If the complement of a digit be defined as (9 - the concerned digit), then (10n - 1) - N is obtained by complementing the digits of N.

Therefore, the 10’s complement of the number N is obtained by subtracting each digit of the number from 9 and then adding 1 to the LSD of the number so formed.

For instance, the 10’s complement of 172 is (827 + 1) or 828 and that of 405 is (594 + 1) or 595.

For the binary number system the radix complement is the two’s complement. The 2’s complement of a binary number is obtained by subtracting each bit of the number from the radix diminished by 1 i.e. from (2 - 1) or 1 and adding an 1 to the LSB. The application of this rule is very simple. We have to just change 1 to 0 and 0 to 1 in every bit and then add 1 to the LSB of the number so formed. For example, the 2’s complement of the binary number 11011 is (00100 + 1) or 00101 and that of 10110 is (01001 + 1) or 01010.

If the number be in signed magnitude representation, it is positive if the MSB is 0 and negative if the MSB is 1. The decimal equivalent of a 2’s complement binary number, in the case of signed-magnitude representation, is computed in the same way as for an unsigned number except that the weight of the MSB is -2n-1 instead of +2n-1 for an n-bit binary number.

Let us observe some examples of 8-bit binary numbers and their 2’s complement are shown below:

2.3 Binary addition, Binary subtraction

Binary arithmetic is essential part of all the digital computers and many other digital system.

Binary Addition

It is a key for binary subtraction, multiplication, division. There are four rules of binary addition.

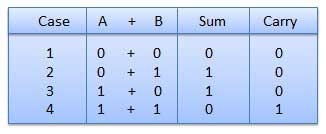
In fourth case, a binary addition is creating a sum of (1 + 1 = 10) i.e. 0 is written in the given column and a carry of 1 over to the next column.

Example − Addition

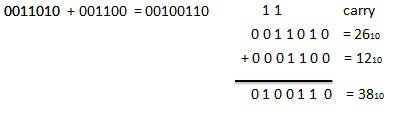
Binary Subtraction

Subtraction and Borrow, these two words will be used very frequently for the binary subtraction. There are four rules of binary subtraction.

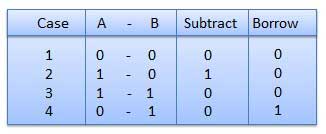
Example − Subtraction

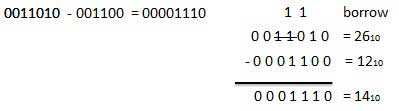
Binary Multiplication

Binary multiplication is similar to decimal multiplication. It is simpler than decimal multiplication because only 0s and 1s are involved. There are four rules of binary multiplication.

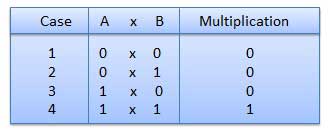
Example − Multiplication

Binary Division

Binary division is similar to decimal division. It is called as the long division procedure.

Example − Division

2.4 Representation of alphabets

Text Books:

1. Satinder Bal Gupta & Amit Singla, Fundamental of Computers and Programming in C, Shree Mahavir Book (Publishers), New Delhi

2. Ajay Mittal, Programming in C, ‘A Practical Approach’, Pearson Education.

3. Byron Gottfried, Schaum's Outline of Programming with C, McGraw-Hill

4. E. Balaguruswamy, Programming in ANSI C, Tata McGraw-Hill

5. YashavantKanetkar, Let Us C, BPB Publication.